神秘的非欧几何——非欧世界
2018-05-28刘玮
刘玮
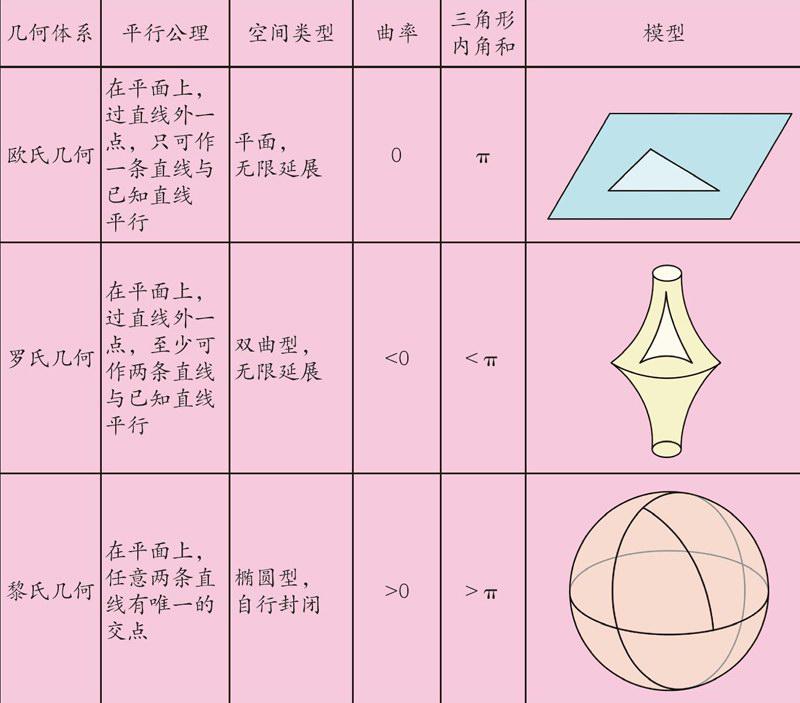
不同曲面上的三角形内角和不同,平行公理也不同,它们是不同的几何世界。平面上的几何是欧几里得几何,双曲面上是罗巴切夫斯基几何,球面上是黎曼几何。
浩天:“黎曼几何还是好理解的,我们就生活在地球上。在海上航行的人明显可以看出海平面的弯曲,但是不能说我们的空间也这么弯曲了吧?罗氏几何的双曲空间很难想象。”
“历史上数学家们提出过许多模型来实现罗氏几何。”鹏飞把罗氏几何模型向浩天作了简介。
第一个是贝尔特拉米模型,就是右页表中的模型,即由曳物线(什么是曳物线?感兴趣的同学可在“中学科技”微信公众号回复“曳物线”,获得解释)旋转而成的伪球面,伪球面上的测地线就是非欧几何中的直线。
第二个模型是克莱因给出的,他将无穷大的欧氏平面用一个有限的圆来表示,圆的边界就是无穷远,圆中的任意一条弦都是一条直线。他是这么定义两点间距离的:

显然,如果A点非常接近圆边界上的无穷远点A',则A、B两点间的距离就会趋于无穷大。同理,若B点接近边界,A、B两点间的距离也会趋于无穷大。这样的圆就是一个非欧平面。

版画家埃舍尔的作品《圆的极限IV》就是根据克莱因模型画的,相当于铺砌整个欧氏平面的无数黑色魔鬼和白色天使被压缩在克莱因的圆形非欧平面里,其实每一个魔鬼或天使大小都相等。
第三个当属最优美自然的庞加莱模型。与克莱因模型一样,庞加莱模型的非欧平面也是一个圆,边界同样是无穷远,但与克莱因模型不同的是,庞加莱模型把圆中垂直于圆周的圆弧(圆的直径是这种圆弧的特例)视为非欧几何中的直线。

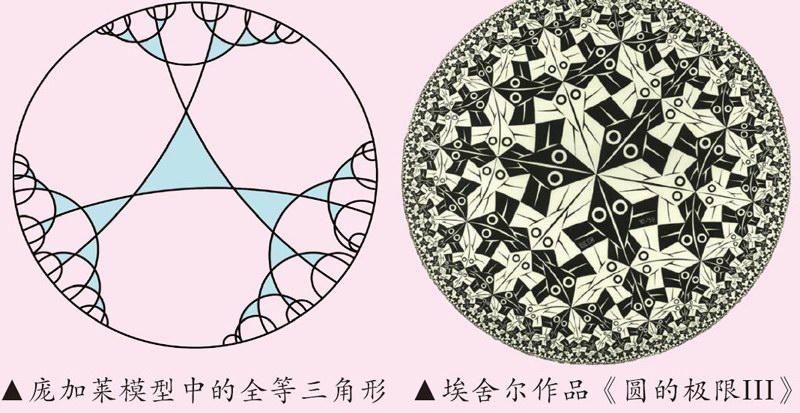
从图中可以直观地看出,罗氏几何中的三角形ABC内角和小于π,过直线外的一点有不止一条非欧直线与已知直线不相交。
埃舍尔的作品《圆的极限III》是根据庞加莱模型画的,相当于铺砌整个欧氏平面的无数条鱼被变形到庞加莱模型的圆形非欧平面里。
浩天:“这有什么意义呢?这只不过是数学家想像的理想数学模型!我们生活的世界到底属于哪一种几何体系?何不实际测量一下呢?”
鹏飞:“1919年,英国物理学家爱丁顿带领一支天文学远征队来到非洲普林西比岛,对正在发生日全食的太阳附近的恒星位置进行观测,并在夜间再次观测这些恒星的位置,结果发现两颗星的角距离在有太阳和没有太阳的情况下,相差1.61±0.3角秒,而爱因斯坦的理论计算值为1.75角秒(爱因斯坦广义相对论认为,在大质量天体附近,时空被弯曲,空间不再是平直的欧式空间)。此后又作了各种观测,都得到了相近的结果。”
“根據光线弯曲的形状看,大质量天体附近的空间应该是椭圆空间,适用黎氏几何,三角形内角和大于π。”浩天说,“而在两个大质量天体中间,空间向两个方向弯曲,是个双曲空间,适用罗氏几何,三角形内角和小于π。”
鹏飞感叹道:“宇宙中充满了星系和天体,我们的宇宙在大范围来看没有平坦的地方,只在小区域内才有可能满足欧几里得几何。”
“天人合一!”浩天脱口而出,“我们的宇宙空间正如我们的身体表面,没有哪个地方是绝对平坦的,脑袋满足黎氏几何,而脖子则满足罗氏几何,鼻尖是黎氏空间,鼻根却是罗氏空间……哈哈,太有意思了!”