旋风分离器流场分析与结构优化的数值模拟

谭礼斌, 袁越锦, 黄 灿, 余千英, 唐 琳, 董继先

(1.重庆隆鑫通用动力股份有限公司 技术中心基础研究所, 重庆 400039； 2.陕西科技大学 机电工程学院, 陕西 西安 710021)

0 引言

旋风分离器是一种结构简单、运行状况稳定、颗粒分离率高的净化处理设备，目前在环境、化工行业应用广泛.旋风分离器的工作原理是通过气体在其内部运动形成旋转气流，颗粒在高速旋转气流的带动下由于受到离心力的作用而被分离.旋风分离器内部流场比较复杂，采用一般的实验研究无法明确认识其内部流场的分布情况，了解其分离机理.采用计算流体力学(CFD)仿真分析软件对其内部流场分布情况进行数值模拟研究，对了解旋风分离器的工作原理、分离特性及结构优化设计都具有非常重要的指导意义.

国内外许多研究学者采用科学的仿真分析技术对旋风分离器的内部流动情况进行了数值模拟分析和实验研究[1-7].祝华腾等[8]采用Fluent软件，用雷诺应力湍流模型对不同结构的旋风分离器进行了模拟分析，得出增设内部构件可削弱二次涡对流场的影响.赵立正等[9]研究了排气芯管直径、插入深度及偏心位置对旋风分离器分离特性的影响.王江云等[10]采用RSM湍流模型、DPM模型和冲蚀模型研究了旋风分离器内气、固冲蚀壁面的速率.Ma L等[11]采用CFD计算方法分析了入口漩涡流处颗粒排列情况对旋风分离器分离效率的影响.Sun X等[12]采用响应曲面设计对Stairmand型旋风分离器进行结构参数优化设计，为旋风分离器的结构设计提供了一定的参考.

某公司700 m3/h沼气池预处理设备旋风分离器的目的是对沼气中5 um、10 um、20 um、50 um颗粒进行分离，净化沼气，提高沼气燃用性能.旋风分离器气体入口处方形截面速度可允许的范围为15～25 m/s，压力损失低于5 kPa.本文采用计算流体力学(Computational Fluid Dynamics,CFD)方法对旋风分离器进行数值模拟，研究其对沼气中5 um、10 um、20 um、50 um颗粒的分离率.为了提升旋风分离器对沼气的净化效果，本文分析了旋风分离器不同结构参数对颗粒分离率的影响，提出旋风分离器结构优化的方案，使沼气中10 um以上粒径的颗粒分离率达到90%以上.

1 物理模型

旋风分离器设备采用Creo3.0(美国PTC公司)建模获得,如图1(a)所示.采用ANSYS SPACECLAIM 2016(美国ANSYS公司的3D高效前处理软件)对旋风分离器设备模型进行体积抽取处理，获得旋风分离器的计算域模型如图1(b)所示.采用流体分析软件STARCCM+ 11.02(美国西递安科公司)中网格划分模块对旋风分离器计算域进行网格划分，完成后的网格模型如图1(c)所示，体网格数量约60万.旋风分离器现方案的参数为：筒体主体直径269 mm，筒体长度453 mm，排气芯管直径168 mm，排气芯管插入深度198 mm，颗粒收集口直径110 mm，锥体段长度615 mm，气体入口圆形直径168 mm，气体入口处方形截面尺寸为高156 mm、宽76 mm，颗粒收集器直径300 mm、高300 mm.为了对旋风分离器的流场分布进行详细分析，本文构建了相应的截面，各截面示意图如图2所示.

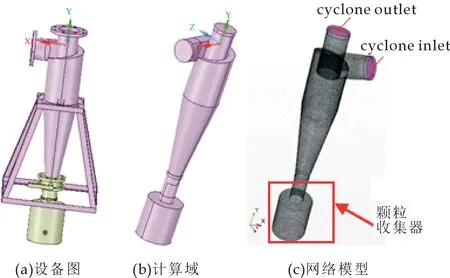
图1 旋风分离器模型

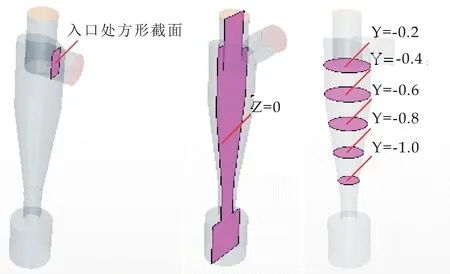
图2 各截面示意图

2 数学模型

2.1 基本控制方程

旋风分离器内部流动为各向异性的漩涡流动，雷诺应力模型摒弃了紊流各向同性的假设，常用于模拟高速旋流、涡流等，可满足旋风分离器内旋转气流的数值计算，因此本文采用雷诺应力湍流模型(RSM：Reynolds Stress Model)进行气相流场的数值模拟，气相和颗粒相间的耦合采用拉格朗日多相流模型(LPM：Lagrangian Multiphase Model)进行求解.求解过程中运用到的基本控制方程如下：

(1)连续性方程

(1)

式(1)中：ui为流体速度，m/s；ρ为流体密度，kg/m3.

(2)动量守恒方程(N-S方程)

(2)

(3)雷诺应力方程[13]

(3)

式(3)中：Cij表示对流项；DT,ij代表分子量粘性扩散项；DL,ij代表湍流扩散项；pij代表雷诺应力产生项；φij代表压力应变项；εij代表粘性扩散耗散项.

2.2 颗粒运动方程

颗粒运动方程由牛顿第二定律获得[14]：

FMA+FG+FC

(4)

式(4)中：mp为颗粒质量，kg；vp是颗粒运动速度，m/s；FD是曳力，FM是质量力，FP是压力梯度力，FBA是Basset力，FSA是Saffman力，FMA是Magnus力，FG是重力，FC是颗粒相间相互作用和颗粒相与壁面相互作用所产生的碰撞力或摩擦力，力的单位都为N.

3 模型求解

本文模拟过程采用瞬态模拟，瞬态模拟的时间步长设置为0.001 s，内迭代步数设置为10步，瞬态最大求解时间为5s.模拟过程中首先计算旋风分离器气相流场，气相流场计算收敛后再激活拉格朗日多相流模型和颗粒入射源，进行颗粒相的数值模拟计算.旋风分离器气相入口边界为速度入口，速度为8.8 m/s(由沼气处理量计算获得).沼气为混合气，密度约为1 kg/m3，气体出口边界为压力出口，压力为-5 kPa(实际运行工况)，壁面设置为无滑移壁面.采用拉格朗日多相流模型(LPM)进行颗粒相模拟，颗粒密度为200 kg/m3，颗粒相的速度与气体速度相同，相间无相对滑移速度.颗粒入射方式为平面入射源(part surface injection)，入射平面为气相入口面，颗粒相均匀地分布在气体入口平面，共1 004个入射点源(点源数目是由该平面面网格数量决定的，对不同结构的旋风分离器采用相同基本网格控制参数进行网格划分，可保证气体入口面面网格数相同)，每个颗粒从面网格中心摄入.每个点源向旋风分离器内部入射5个粒子，共计入射4 020个粒子(单一粒径).为了研究5 um、10 um、20 um、50 um四种粒径的分离率，本文共设置颗粒粒径分别为5 um、10 um、20 um、50 um的四个入射源.

4 模拟结果及分析

4.1 压力损失变化分析与模型验证

旋风分离器压力损失是评估旋风分离器性能的指标之一.压力损失的计算公式为：

(5)

式(5)中：ρg为气体密度，kg/m3;vi为气体入口处方形截面内速度(气体入口为圆形面，速度8.8 m/s，根据质量守恒定律计算获得气体入口处方形截面内速度值)；α为阻力系数，α可由经验模型计算获得[15].

图3表示压力损失的计算值与经验模型获得的理论值对比曲线图.从图3可以看出，计算值与Ca Model和Di Model理论值基本吻合，与其余两个理论模型存在一定的误差，最大误差约为9.85%.表明本文建立的计算求解模型是有效的.图中15 m/s为沼气处理量700 m3/h时旋风分离器气体入口处方形截面内的面平均速度值.从图3中可以看出，在气体入口面相同时，气体的处理量越大，气体入口处方形截面内的平均速度值越大，旋风分离器的压力损失也越大，随着速度的增大，压力损失增加幅度增大，容易造成颗粒对壁面的冲击腐蚀，降低旋风分离器的使用周期.因此，在工程应用中，为了保证旋风分离器的工作性能，会对气体的处理量(即入口速度)和压力损失有相应的限制范围.

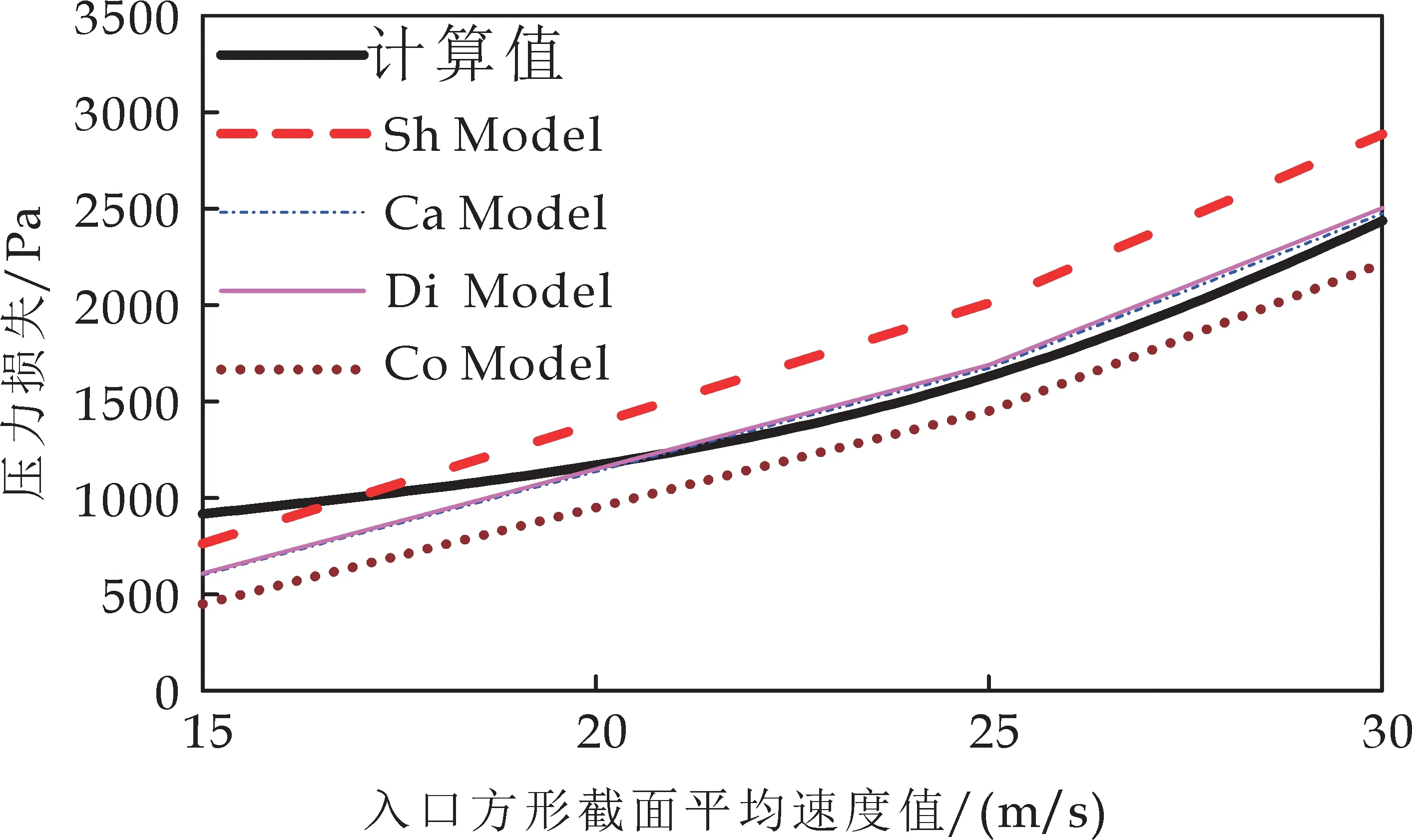
图3 压力损失计算值与模型理论值对比曲线

4.2 气相流场分布

4.2.1 压力分布

图4表示Z=0截面的压力分布云图.静压沿径向位置(旋风分离器壁面至轴中心的距离)呈现出较好的轴对称分布特性，静压随径向位置的减小而减小，在轴中心处的静压值远低于气体入口处的静压值.动压的分布未呈现出类似静压的轴对称性.动压分布趋势与气相流场速度分布基本相同，原因是动压与流体速度之间是直接相关的，动压Pd=ρgv2/2.动压分布云图能间接反映气相流场速度的分布规律.总压的分布情况与静压分布极其类似，都呈现出较好的轴对称性，总压随径向位置的减小而减小，轴中心处总压值远低于壁面和气体入口处的总压值.

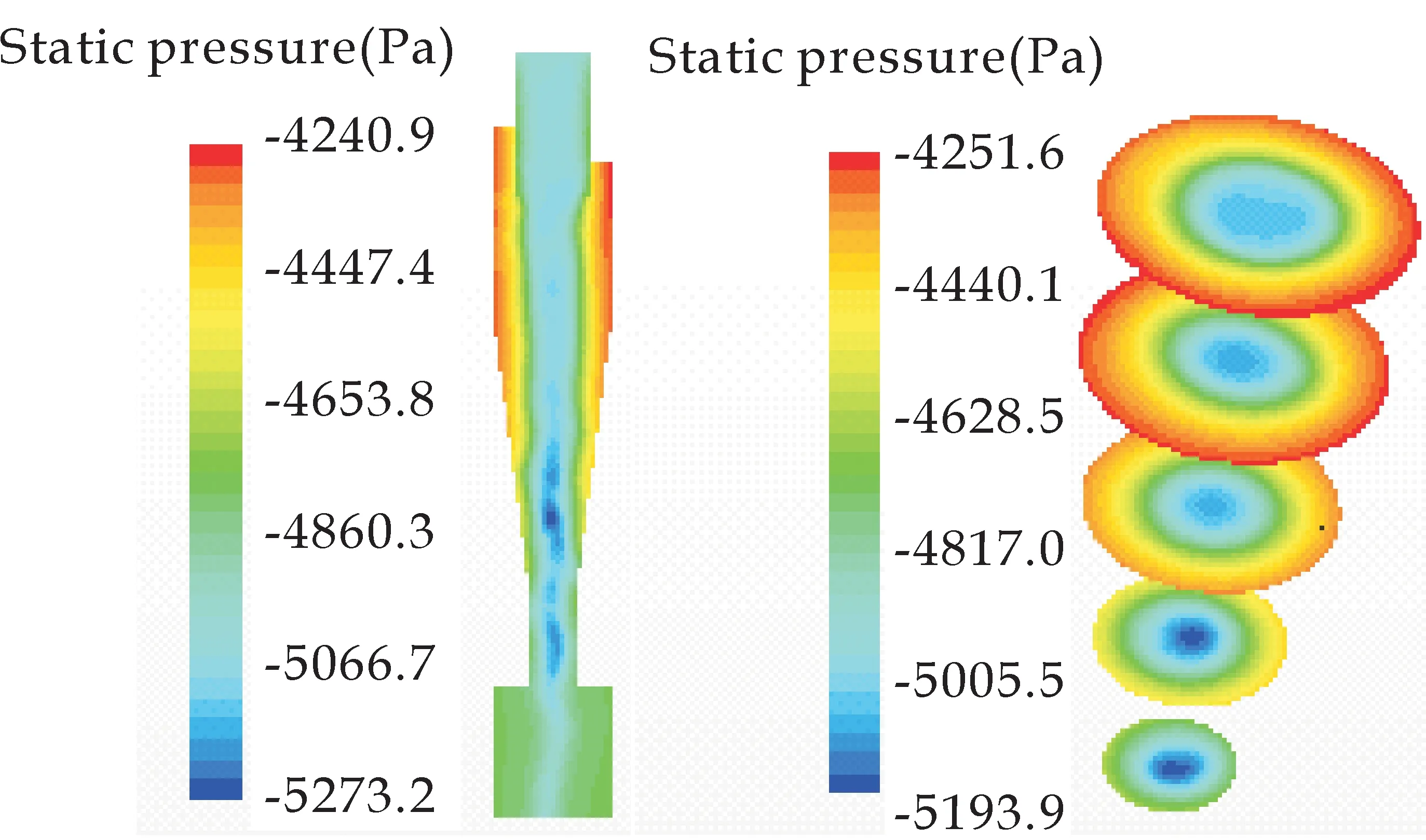
(a)各截面的静压分布云图

(b)各截面的动压分布云图

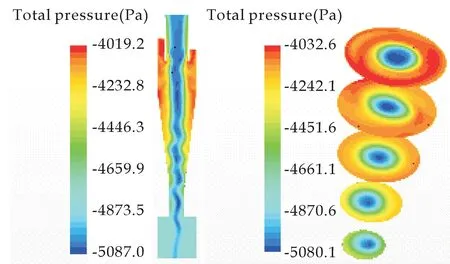
(c)各截面的总压分布云图图4 气相流场的压力分布

图5表示压力随径向位置(旋风分离器壁面至轴中心的距离)的变化曲线图.静压沿径向位置的变化曲线呈现出“V”形形状，动压沿径向位置的变化曲线呈现出“M”形状.总压沿径向位置的变化趋势与静压沿径向位置的变化趋势一致.采用面积平均法(Surface Average Method)计算出该旋风分离器运行时产生的压力损失为0.918 kPa.

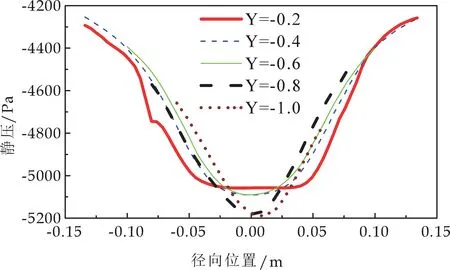
(a)静压沿径向位置的变化曲线图

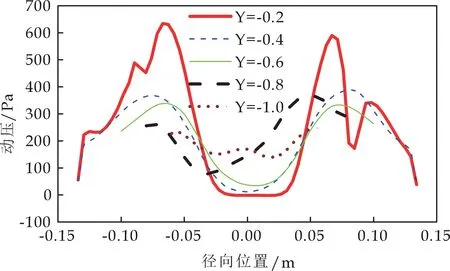
(b)动压沿径向位置的变化曲线图

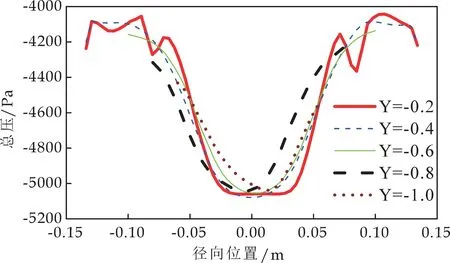
(c)总压沿径向位置的变化曲线图图5 压力沿径向位置的变化曲线图

4.2.2 速度分布

图6表示旋风分离器气相流场的速度分布.气相流场的速度分布与气相流场的动压分布基本一致.从速度矢量图可以看出，气流在旋风分离器流动主要形成了双层漩涡流动，外部形成向下旋转的旋流，中心则形成向上旋转的旋流，两者的旋转方向相同[16].在排气芯管附近的气流速度比较大，分离器旋转气流的湍流扰动性较强.

4.3 流场湍流特性研究

湍动能表示单位质量的流体在流动过程中由于湍流脉动所形成的动能，主要是由雷诺切应力做功而产生的.图7表示气相流场的湍动能沿径向位置的变化曲线.从图7可以看出，旋风分离器内部壁面处的湍动能较小，湍动能由上往下基本呈现出减小的趋势.筒体段分离空间的中心区域(Y=-0.2 m)的湍动能较大，因此该区域内产生的能量损耗越大.

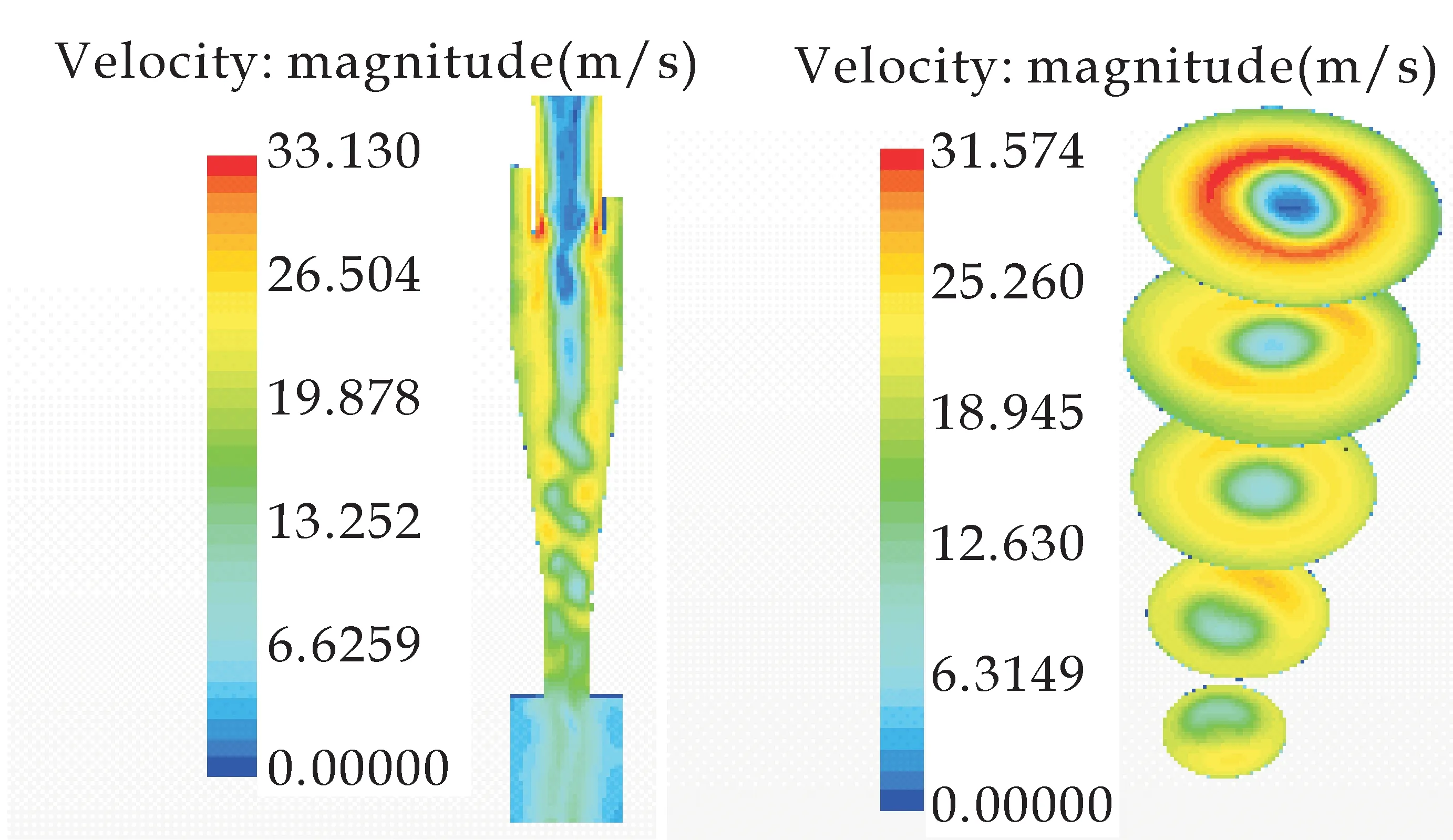
(a)各截面速度分布云图

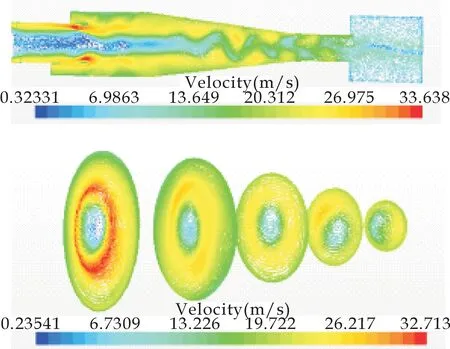
(b)各截面速度分布矢量图

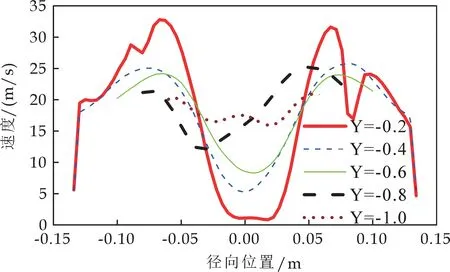
(c)各截面速度沿径向位置的变化曲线图图6 气相流场的速度分布

图8表示气相流场的湍动耗散率沿径向位置的变化曲线.从图8可以看出，旋风分离内部壁面处的湍动耗散率较大，中心区域的湍动耗散率较小.对比分析图7和图8可以看出，湍动能与湍动耗散率沿径向位置的分布都基本呈现出较好的轴对称性.湍动能与湍动耗散率分布趋势存在差异，其原因是由于旋风分离器内旋转气流流动的各向异性特性引起的[17].

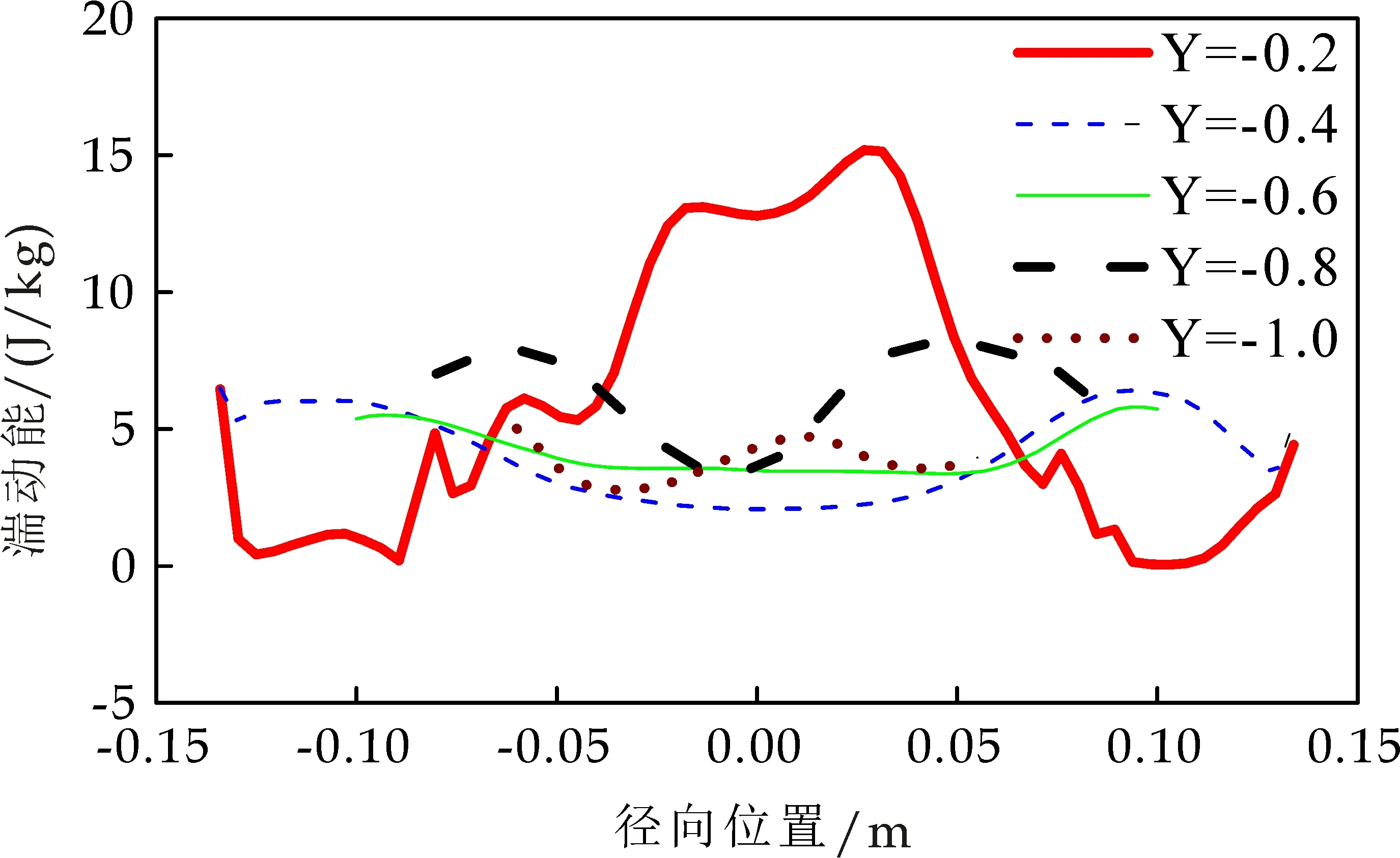
图7 湍动能沿径向位置的变化曲线图

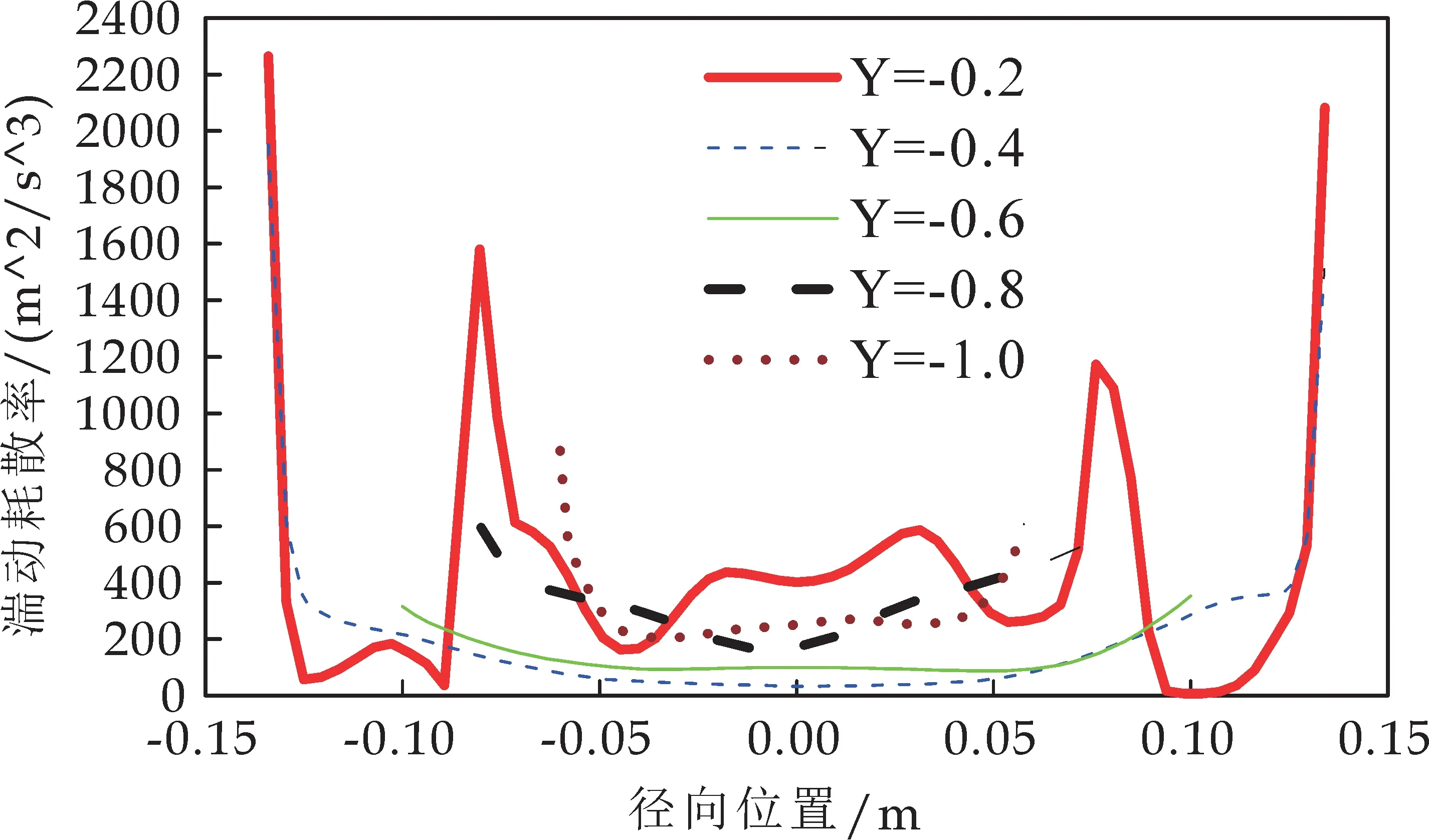
图8 湍动耗散沿径向位置的变化曲线

4.4 颗粒分离率

颗粒运动到排气芯管上端面视为逃逸；颗粒运动到颗粒收集口截面视为被颗粒收集器收集.颗粒分离率的计算公式为：

(6)

式(6)中：Cc代表颗粒收集器收集到的颗粒数目；Ct表示进入旋风分离器的颗粒总数.

表1为旋风分离器现方案各粒径颗粒的分离率.旋风分离器现方案下各粒径颗粒的分离率分别为39.71%、71.52%、90.77%、100%，5 um和10 um颗粒的分离效果不好.图9表示不同颗粒密度下旋风分离器现方案的颗粒分离率.从图9可以看出，颗粒粒径越大，分离率越好；颗粒密度越大，分离率越好.原因是颗粒粒径越小，质量小，在旋风分离器中形成的离心力较小，不易被分离.同理，同一粒径颗粒，颗粒密度越大，质量越大，在旋风分离器中受到的离心力作用越大，越易分离.

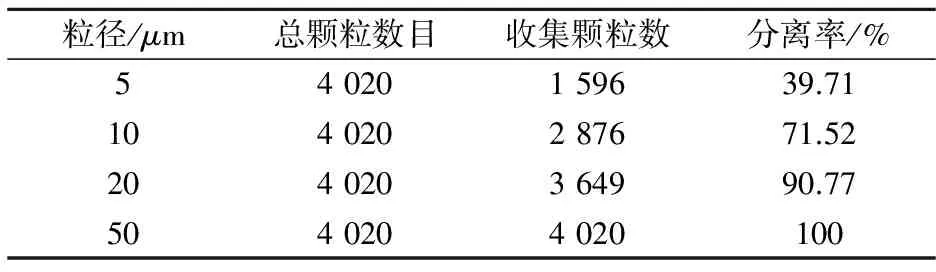
表1 旋风分离器现方案的颗粒分离率

4.5 旋风分离器结构参数对颗粒分离率的影响

4.5.1 排气芯管直径

图10为不同排气芯管直径下颗粒分离率的对比曲线.从图10可以看出，排气芯管直径减小，颗粒分离率增大，排气芯管直径增大，颗粒分离率减小.原因是排气芯管直径增大，易造成芯管外壁附近处的速度变大，从而会卷吸走部分粒径较小的颗粒，降低其分离率.排气芯管直径减小，旋风分离器内旋流面积减小，对颗粒的携带作用减弱，分离器轴中心处的颗粒被内旋流带离旋风分离器的机率减小，促使更多的颗粒在壁面附近被捕集，最后由收集器收集，因此适当减小旋风分离器排气芯管直径有利于颗粒分离[13].排气芯管直径为138 mm时，压降为1.3 kPa.

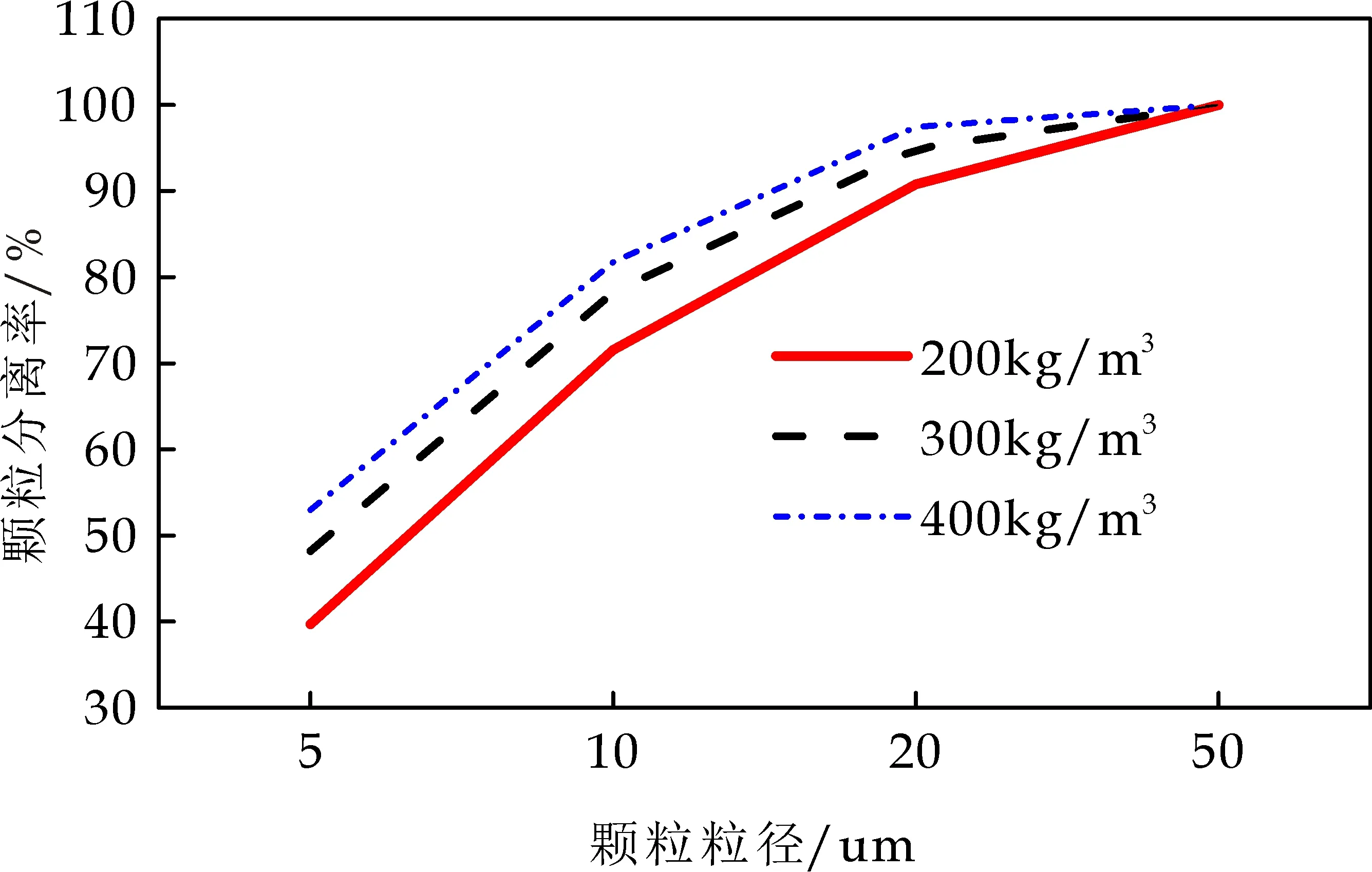
图9 不同颗粒密度下颗粒分离率曲线图

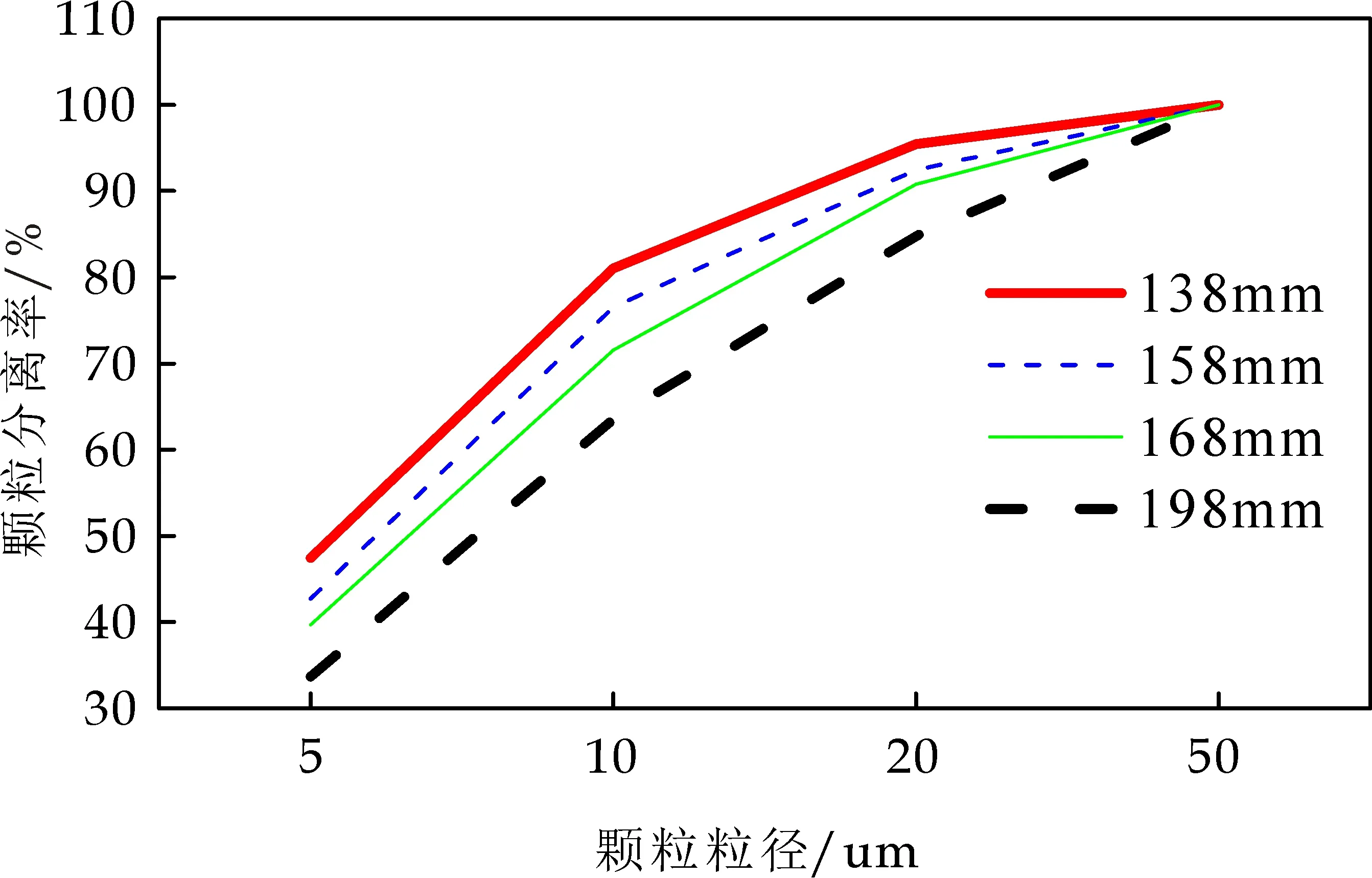
图10 不同排气芯管直径下颗粒分离率曲线图

4.5.2 排气芯管插入深度

图11为不同排气芯管插入深度下颗粒分离率的对比曲线.从图11可以看出，排气芯管插入深度为168 mm时，各粒径颗粒的分离率最好.原因是排气芯管插入深度太短容易造成"短路流"，部分颗粒会跟随短路流直接进入排气芯管，最后逃逸，降低了颗粒分离率；排气芯管插入深度太长，流动中会产生较大的压力损失，且颗粒的分离率也会受到影响[16].排气芯管插入深度为168 mm时，压降为0.891 kPa.

4.5.3 颗粒收集口直径

图12为不同颗粒收集口直径下颗粒分离率的对比曲线.从图12可以看出，颗粒收集口直径为120 mm，各粒径颗粒的分离率有所提高，颗粒收集口直径为100 mm、130 mm时各粒径颗粒的分离率与原始结构下颗粒分离率相差不大.颗粒收集口直径为120 mm时，压降为0.916 kPa.颗粒收集口附近的速度仍然具有较大的值，颗粒收集口附近的旋转气流比较剧烈，容易形成颗粒收集口处颗粒夹带返混的现象，因此该旋风分离器的收集器口存在一段直管，将从锥体段底部流出的旋转气流引入直管内进一步进行颗粒分离，最后收集器口捕集更多颗粒，提高颗粒分离率[18].

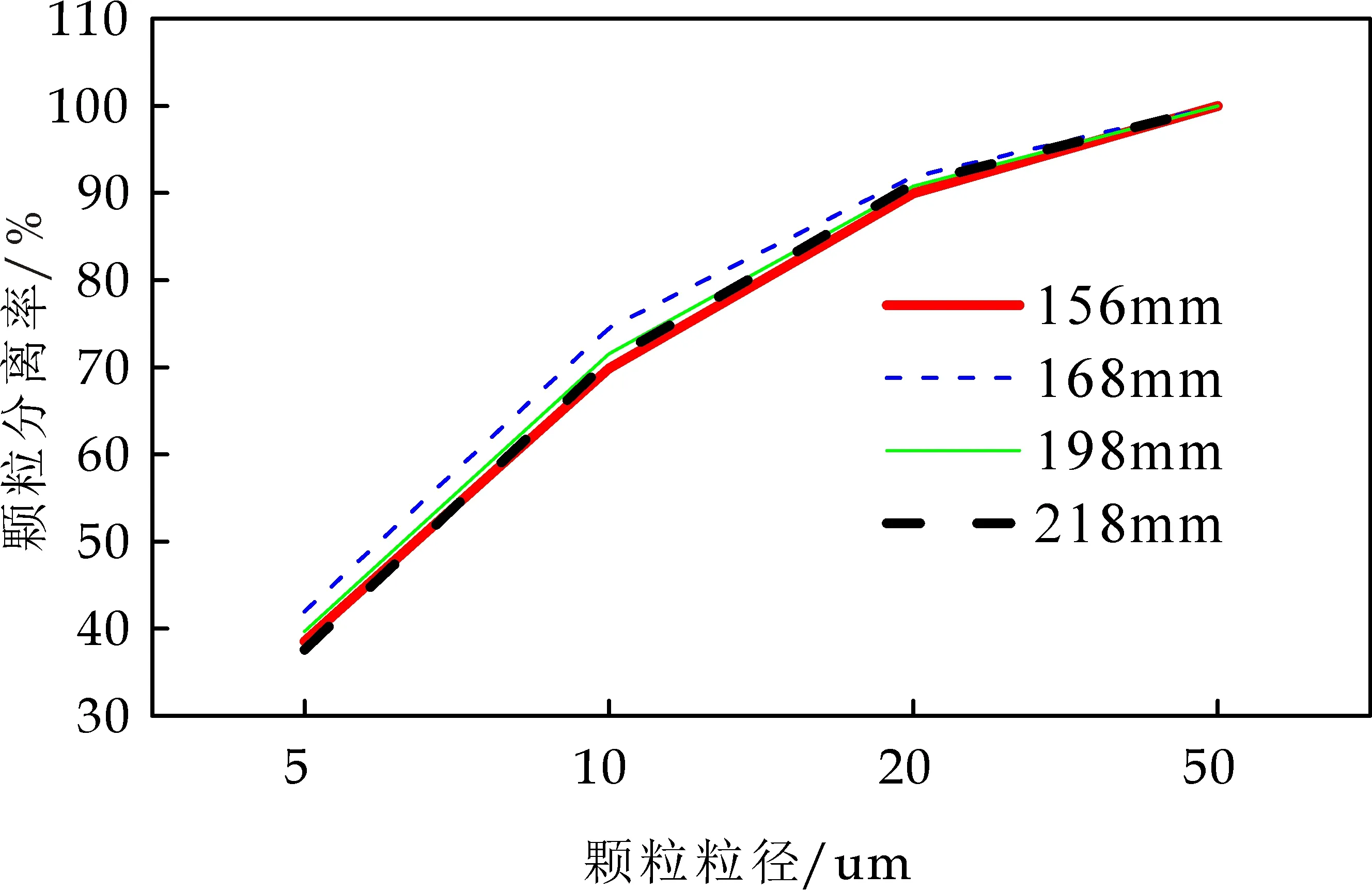
图11 不同排气芯管插入深度下颗粒分离率曲线图

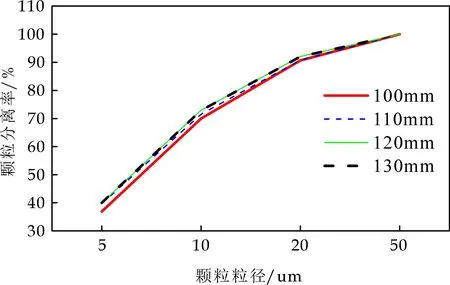
图12 不同颗粒收集口直径下颗粒分离率曲线图

4.5.4 筒体长度

图13为不同筒体长度下颗粒分离率的对比曲线.从图13可以看出，筒体长度增大，各粒径颗粒的分离效率增加，增加幅度比较平缓.当筒体长度为538 mm时，颗粒分离率分别为41.08%、74.77%、93.13%、100%，压降为0.904 kPa.采用面积平均法计算出四个结构下的压降分别为0.958 kPa、0.918 kPa、0.909 kPa、0.904 kPa，筒体长度增加，压力损失降低.原因是在气体处理量一定的情况下，筒体越短，旋风分离器壁面产生的摩擦力越小，分离器内的旋转气流越强，气体进入排气芯管中心的静压降低，静压更有效地转换成动压，促使压降增大[19].

4.5.5 锥体段长度

图14为不同锥体段长度下颗粒分离率的对比曲线.从图14可以看出，在旋风分离器初始结构下减小或增加锥体长度值，对颗粒分离率几乎没有影响.三个锥体段长度的旋风分离器对各粒径颗粒的分离效果相差不大.通过修改旋风分离器锥体段长度与筒体直径间的相对比例值，可防止旋风分离器内强湍流特性的旋转气流将已分离的颗粒重新卷起，提高颗粒分离率.工程上，旋风分离器锥体段的取值范围一般为筒体直径的1.5～2.5倍[20].

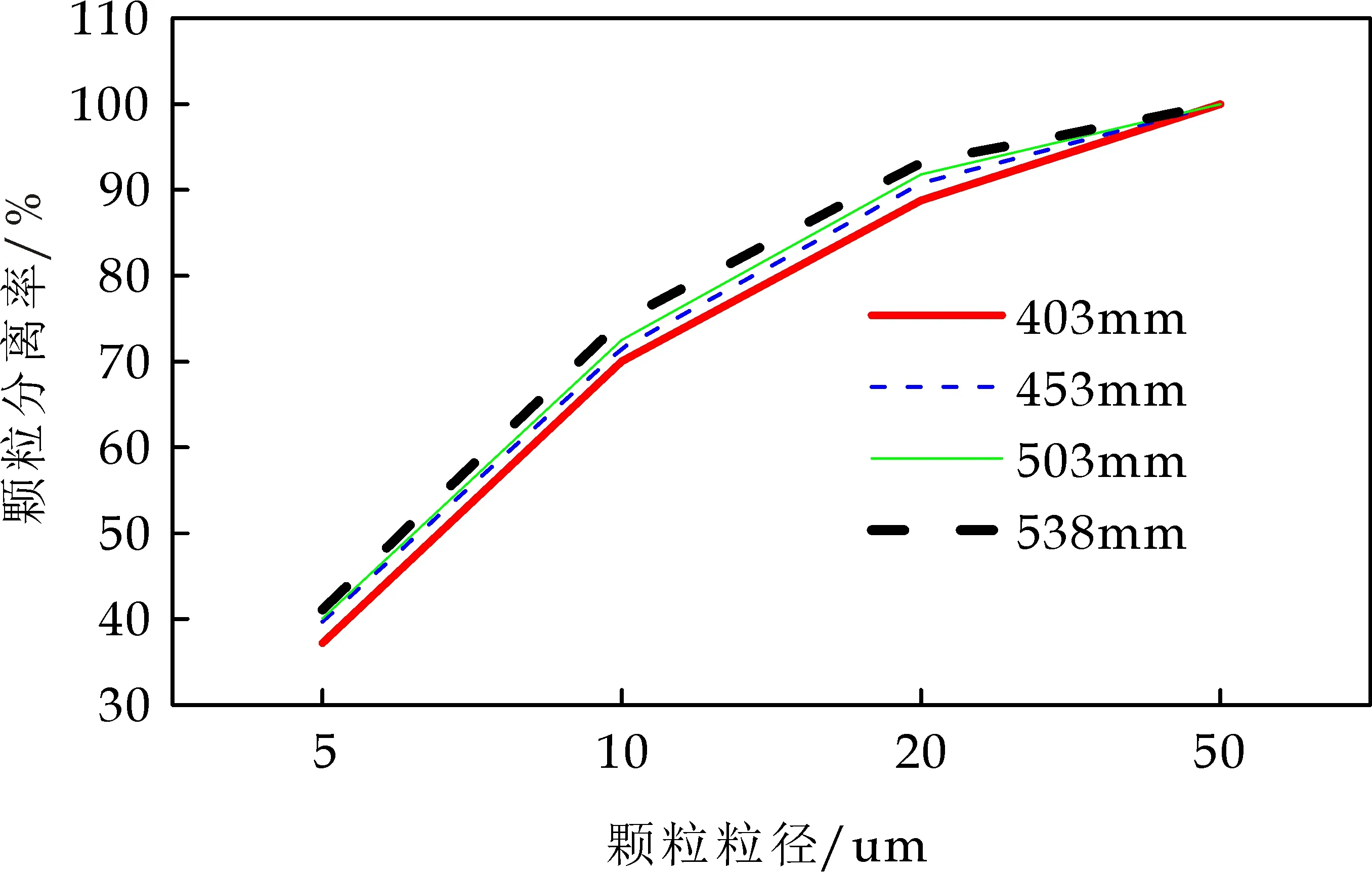
图13 不同筒体长度下颗粒分离率曲线图

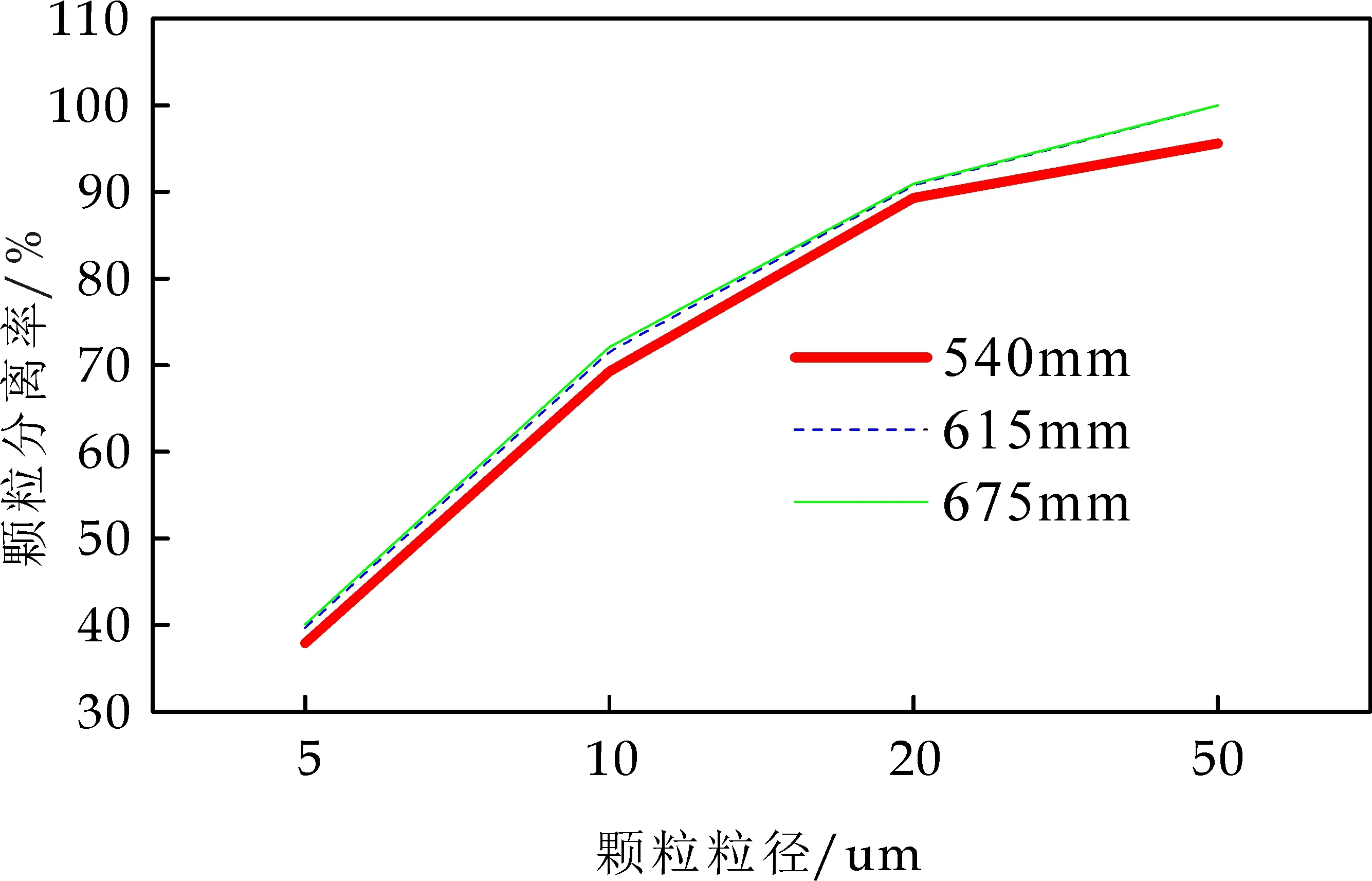
图14 不同锥体段长度下颗粒分离率曲线图

4.5.6 气体入口方形截面尺寸

采用四种不同入口方形截面尺寸进行模拟分析，得出不同气体入口方形尺寸下颗粒分离率的对比曲线,如图15所示.图中“a”表示入口处方形截面的高度值，“b”表示入口处方形截面的宽度值.从图15可以看出，气体入口方形截面尺寸对颗粒分离率的影响最大.四种不同入口方形截面尺寸中前三种截面尺寸下的颗粒分离率相差不大，而第四种入口方形截面尺寸下各颗粒分离率明显提升.四种不同入口方形尺寸结构的旋风分离器在运行中的压力损失分别为0.858 kPa、0.918 kPa、0.996 kPa、1.6 kPa.造成这种现象的原因是前三种入口方形截面面积一致，气体处理量相同的情况下速度分布基本相同，产生的离心力场相差不大，因此颗粒分离率和压力损失变化不明显；而第四种入口方形截面面积较旋风分离器初始结构减小，在气体处理量一定的情况下，入口方形面积减小，速度增大，离心力场越大，颗粒越易被分离.同时，速度增大，压力损失增大，过大的压力损失易造成旋风分离器壁面的冲击腐蚀，影响旋风分离器的使用寿命[21].入口方形高度为134 mm，宽为54 mm时，各粒径颗粒的分离率明显增大，5 um、10 um、20 um、50 um的颗粒分离率分别为51.86%、94.62%、100%、100%.

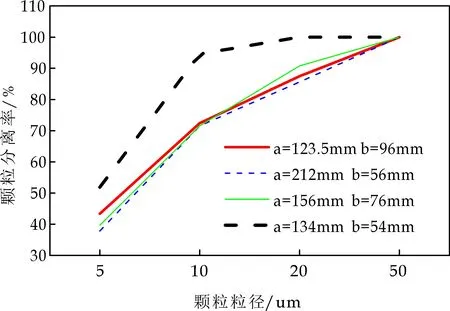
图15 不同入口方形尺寸下颗粒分离率曲线图

5 旋风分离器结构优化方案

综合分析旋风分离器各结构参数对颗粒分离率的影响的模拟结果，得到气体入口处方形截面尺寸对颗粒分离率的影响最大，排气芯管直径、颗粒收集口直径对颗粒分离率的影响较大，筒体长度、排气芯管插入深度对颗粒分离率有一定影响，而现结构下改动锥体段长度对颗粒分离率的影响不明显.为满足10 um及以上粒径颗粒的分离率，依据旋风分离器的不同结构参数对颗粒分离率的影响程度，提出以下三个优化方案(Opt)：

(1)排气芯管直径为138 mm，气体入口方形截面尺寸为高134 mm、宽54 mm，颗粒收集口直径为120 mm.

(2)排气芯管直径为138 mm，颗粒收集口直径为120 mm，筒体长度为538 mm，排气芯管插入深度为168 mm.

(3)在(2)的基础上增改：气体入口方形截面尺寸为高134 mm、宽54 mm.

表2为旋风分离器三个优化方案各粒径颗粒的分离率.三个优化方案各粒径颗粒的分离率都有明显的提升，其中Opt1、Opt3中10 um及以上粒径颗粒的分离率均达98%以上，压降分别为2.213 kPa、2.082 kPa，压降增大的原因是该两个方案中都改动了入口处方形截面尺寸大小，面积减小，截面内平均速度增大，造成压力损失增大；Opt2中10 um粒径颗粒的分离率为86.5%，基本符合沼气预处理设备旋风分离器对颗粒分离率的提升目标.该旋风分离器的运行时压降允许范围为低于5kPa，因此，在压降允许的范围内，确定优化方案一为旋风分离器的最佳优化方案.

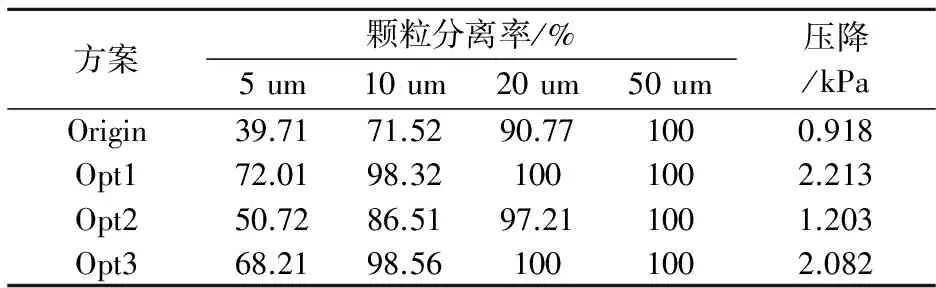
表2 旋风分离器优化方案(Opt)的颗粒分离率

6 结论

(1)采用RSM模型和LPM模型对旋风分离器内气固两相耦合流动机理及颗粒运动机理进行了瞬态模拟研究，验证了RSM模型可有效地模拟旋风分离器内各向异性的高速强漩涡流动，压力损失计算值与经验模型理论值基本吻合，表征本文所构建的旋风分离器计算域模型可有效地模拟旋风分离器气固两相耦合流动过程.

(2)对旋风分离器内气相流场模拟结果分析，得出旋风分离器气相流场中静压和总压分布基本一致，都呈现出较好的轴对称性，静压值和总压值沿径向位置的变化曲线呈现“V”型，静压值和总压值随径向位置的减小而减小，轴心处的静压值和总压值远低于壁面处的静压值和总压值.气相流场中的动压分布与速度分布趋势基本相同，沿径向位置的变化曲线呈现“M”型.湍动能与湍动耗散率沿径向位置的分布都基本呈现出较好的轴对称性.

(3)气相和颗粒相的耦合模拟结果显示5 um、10 um、20 um、50 um颗粒的分离率分别为39.71%、71.52%、90.77%、100%，5 um和10 um颗粒的分离效果不好，颗粒粒径越大，颗粒分离率越好，颗粒密度越大，对应的颗粒分离率也越大.

(4)通过分析旋风分离器各结构参数对颗粒分离率的影响，得出气体入口处方形截面尺寸对颗粒分离率的影响最大，排气芯管直径、颗粒收集口直径对颗粒分离率的影响较大，筒体长度、排气芯管插入深度对颗粒分离率的影响较小，现结构下改动锥体段长度对颗粒分离率的影响不明显.

(5)依据旋风分离器各结构参数对颗粒分离率的影响程度，提出了三个优化方案并验证了各方案下颗粒的分离率，优化方案一改动排气芯管直径为138 mm、气体入口处方形截面尺寸为高134 mm宽54 mm、颗粒收集口直径为120 mm，各颗粒分离效率最好，10 um及以上粒径颗粒的分离率均达98%以上，压降为2.213 kPa，在旋风分离器运行允许的压降范围内.

[1] 吴广强,孙振雷,刘 伟.旋风分离器的安全性能分析及数值模拟[J].通用机械,2017(5):77-80.

[2] 苏 伟,武晶晶,于建奇,等.旋风分离器的气相流场的性能分析及数值模拟[J].机械制造与自动化,2017,46(3):161-163.

[3] 刘 旭,朱海雷.旋风分离器数值模拟[J].压缩机技术,2016(2):53-57.

[4] 李 铁,郑 瀚,宋济洋,等.旋风分离器数值模拟及结构优化研究进展[J].矿山机械,2014(11):10-13.

[5] 雷 蕾,袁隆基.循环流化床锅炉旋风分离器性能特性数值模拟[J].江苏大学学报(自然科学版),2015,36(2):148-152.

[6] Rahimian M H.Multiphase flow and tromp curve simulation of dense medium cyclones using computational fluid dynamics[J].Journal of Mining & Environment,2013,4(1):67-76.

[7] Luan Y,Sun H.Experimental and numerical study on the resistance performance of an axial flow cyclone separator[J].Mathematical Problems in Engineering,2015,2015:1-9.

[8] 祝华腾,陈光辉,王伟文,等.不同结构的旋风分离器二次涡的数值模拟和分析[J].高校化学工程学报,2017,31(5)：1 062-1 071.

[9] 赵立正,原奇鑫,康志忠,等.超临界循环流化床旋风分离器结构优化数值模拟[J].锅炉技术,2016,47(3):31-37.

[10] 王江云,冯留海,张 果,等.单入口双进气道旋风分离器内冲蚀特性[J].石油学报(石油加工),2016,32(2):289-296.

[11] Ma L,Fu P B,Wu J P,et al.CFD simulation study on particle arrangements at the entrance to a swirling flow field for improving the separation efficiency of cyclones[J].Aerosol & Air Quality Research,2015,15(6S):2 456-2 465.

[12] Sun X,Kim S,Yang S D,et al .Multi-objective optimization of a stairmand cyclone separator using response surface methodology and computational fluid dynamics[J].Powder Technology,2017,320:51-65.

[13] 郑建祥,周天鹤.旋风分离器排气管缩口半径优化的数值模拟[J].流体机械,2015,43(12):28-32.

[14] 马 欣,徐洋洋,徐 洋,等.排气管外延伸长度对旋风分离器性能的影响[J].过程工程学报,2016,16(6):915-921.

[15] 钱付平,章名耀.旋风分离器分离性能的经验模型与数值预测[J].东南大学学报(自然科学版),2005,35(1):35-39.

[16] 刘 琳.旋风分离器内气固两相流数值模拟与稳定性研究[D].杭州：浙江理工大学,2016.

[17] 张海红.旋风分离器流场与分离性能的数值模拟研究[D].郑州：郑州大学,2004.

[18] 韩 婕,刘阿龙,彭东辉,等.旋风分离器两相流动数值模拟研究进展[J].天然气化工(C1化学与化工),2012,37(5):55-61.

[19] 王乐勤,郝宗睿,王循明,等.筒体长度对旋风分离器内流场影响的数值模拟[J].工程热物理学报,2009,30(2):223-226.

[20] 董 敏,刘淑良,杨洪征.结构参数和操作参数对旋风分离器性能的影响[J].选煤技术,2013(6):93-96.

[21] 李 琴,邹 康,刘海东,等.基于颗粒受力的旋风分离器冲蚀机理的研究[J].流体机械,2017,45(3):42-47.