系泊系统的设计

宋 培，潘玉媚，卢敏如，方 睿

（汕头大学数学系，广东 汕头 515063）

0 引言

近浅海观测网的传输节点由浮标系统，系泊系统和水声通讯系统组成.而系泊系统的设计问题就是选取适合的锚链的型号，长度和重物球的质量，尽量减小浮标的吃水深度和游动区域及钢桶的倾斜角.从而令水声通讯系统的设备有较好的工作效果.本文根据2016年全国大学生数学建模竞赛A题给出的某型传输节点各系统中的一些部件规格，锚链型号和参数表，以及传输节点的示意图，尝试解决以下问题：

问题一：某型传输节点选用II型电焊锚链22.05 m，选用的重物球质量为1200 kg.现将该型传输节点布放在水深18 m，海床平坦，海水密度为1.025×103kg/m3的海域.假设海水静止，分别计算海面风速为12 m/s和24 m/s时钢桶和各节钢管的倾斜角度，锚链形状，浮标的吃水深度和游动区域.

问题二：在问题一的假设下，计算海面风速为36 m/s时钢桶和各节钢管的倾斜角度，锚链形状和浮标的游动区域.请调节重物球的质量，使得钢桶的倾斜角度不超过5°，锚链在锚点与海床的夹角不超过16°.

问题三：由于潮汐等因素的影响，布放海域的实测水深介于16 m到20 m之间.布放点的海水速度最大可达到1.5 m/s，风速最大可达到36 m/s.请给出考虑风力，水流力和水深情况下的系泊系统设计，分析不同情况下钢桶，钢管的倾斜角度，锚链形状，浮标的吃水深度和游动区域.

注：题目可到全国大学生数学建模竞赛官方网站http://www.mcm.edu.cn下载

1 模型的假设

为了方便研究，在不改变题目要求的前提下，我们对模型作出以下假设：

（1）在任何情况下，圆柱形浮标始终保持竖直，不发生倾斜；

（2）风速恒定，方向平行于海平面，不同风速下浮标的近海风荷载为恒定值；

（3）钢管，钢桶，锚链的质量分布均匀，锚链之间的连接无长度损失；

（4）海水流动方向平行于海平面，海面没有波浪，并且当地的重力加速度恒为9.8 m/s2.

2 模型的建立与求解

2.1 问题一的分析

袁梦等人[1]系统地进行了系泊系统的动力分析，顺着他们的思路，我们需要综合考虑风力，水流力和水深三个影响因素，在某型传输节点受到不同程度的影响时求解：（A）钢桶和各节钢管的倾斜角度；（B）锚链的形状；（C）浮标的吃水深度和游动区域.

问题给出锚链长度与重物球质量等条件，要求计算不同风速时钢桶和各钢管的倾斜角度，锚链形状，浮标的吃水深度及游动区域.风速确定时，浮标的风荷载和浮力由吃水深度决定，我们设定吃水深度的一个初值，通过考虑整个系统在受力平衡状态下的情况，可以确定各钢管间以及钢桶的拉力及其与水平方向的夹角；再通过重物球的信息可以确定锚链和钢桶连接处的拉力及力与水平方向的夹角；继而用迭代算法确定锚链各链环间的拉力及倾角，而后就可以得出锚链形状，这样我们就解决出（A）和（B）.然后通过不断调整初值，使得计算出的进入海水里的系泊系统的深度与水深的差值小于0.05，得到浮标的吃水深度.当系统受力平衡时浮标游动到离锚水平距离最长的地方，则浮标的游动区域可以确定，从而解决（C）.给出问题一的求解流程图如图1.

图1 问题一的求解流程图

2.1.1 已知条件：传输节点布放在水深18 m，海床平坦，海水密度为1.025×103kg/m3的海域.选用II型电焊锚链22.05 m，重物球质量1200 kg.假定海水静止.

2.1.2 对浮标和钢管进行物理受力分析

（1）把浮标看作质点模型，对浮标进行物理受力分析如图2所示.

在已知浮标在海水静止，海面有风的海域上，我们得出浮标受四个作用力，分别是重力G0，浮力f0，风的作用力F风和第一节钢管的作用力T1.其中θ1表示第一节钢管对浮标的作用力T1与水平方向的夹角，那么第一节钢管的倾斜角度为由于浮标在四个作用力下处于受力平衡状态，可列出如下方程：

整理简化方程（1），得出：

图2 浮标的受力分析图

图3 第一节钢管上方连接点的受力分析图

（2）选取第一节钢管与浮标的连接点对第一节钢管进行物理受力分析如图3所示：

分析后得知第一节钢管同时也受四个作用力，分别是重力G1，浮力f1，浮标对第一节钢管的作用力和第二节钢管对第一节钢管的作用力T2.因为浮标和第一节钢管之间的相互作用力T1和在同一直线上，故与水平方向的夹角也为θ1.此外，把第二节钢管对第一节钢管的作用力T2与水平方向的夹角记作θ2，则第二节钢管的倾斜角度表示为钢管处于受力平衡状态，可列方程如下：

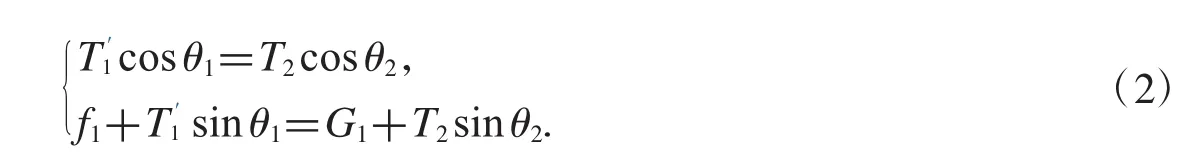
（3）对第二，三，四节钢管的受力分析与第一节钢管相似，均取钢管上方的连接点进行受力分析，以下仅给出受力分析图（图4）：

图4 从左往右分别是第二、第三、第四节钢管上方连接点的受力分析图

同理，第二，三，四节钢管也处于受力平衡状态，可列通用方程如下：

整理简化方程（3）求解出第二，三，四节钢管与水平方向的夹角θi（i＝2，3，4）的正切值通用表达式如下：

（4）对钢桶进行受力分析，分别是对钢桶的上下端点进行受力分析.上端点是钢桶与第四节钢管的连接点，而下端点则是钢桶与锚链首节的连接点.由于重物球挂在钢桶的下方，那么在下端点处可将重物球和钢桶看作整体，故下端点的受力分析采用整体法.钢桶的受力分析图如图5.

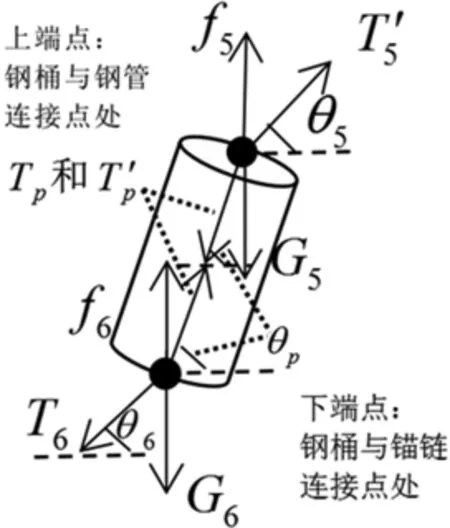
图5 钢桶的受力分析图

图5中，G5和G6分别表示钢桶、重物球的重力，f5和f6分别表示钢桶、重物球所受的浮力，表示第四节钢管对钢桶上端点的作用力，T6表示锚链首节对钢桶下端点的作用力，Tp和分别表示钢桶对第四节钢管的作用力、钢桶对锚链首节的作用力，这两个作用力大小相同而方向相反.由于钢桶和重物球整体处于受力平衡状态，可列方程组如下：

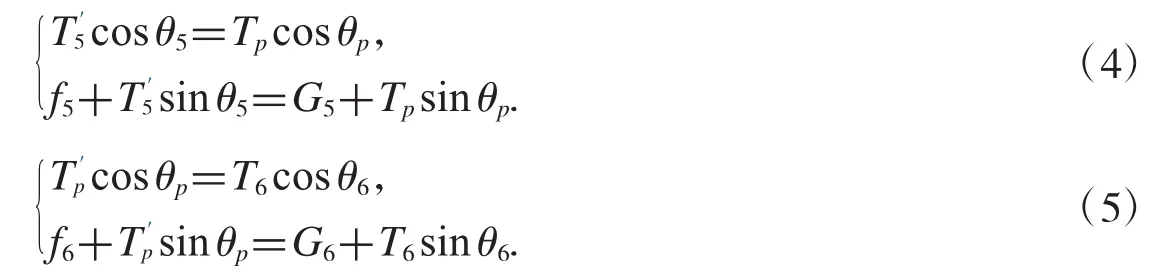
因为Tp和大小相同，整理方程组（4）和（5）可得：

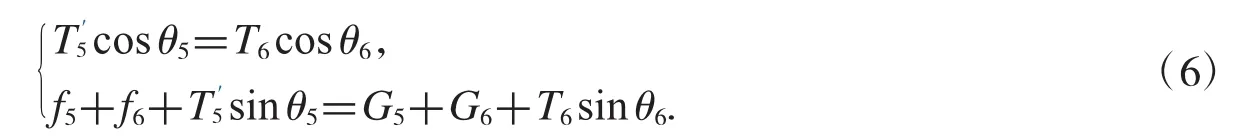
（5）说明：所有的受力分析图中，浮力和重力的方向是确定，但其长短不可表示其大小，力的大小需要通过计算得知；所有受力分析图中，给出的相互作用力T1和以及拉力T6的方向和长短不是某时的真实的情况，而是仅给出大致情况以方便列出受力平衡状态时的方程；同样地，图中给出的各钢管和钢桶与水平方向的夹角 θ1，θ2，θ3，θ4，θ5也都是不表示某时的实际情况，仅为方便分析；根据牛顿第三定律，知是相互作用力，方向相反，大小相同.

2.1.3 建立单点系泊系统二维静力学模型[2]

首先，建立一个关于进入海水里的系泊系统的高度H的模型，将H看作三个部分高度的总和，分别是浮标的吃水深度h，钢管和钢桶在竖直方向上的投影长度L以及锚链在竖直方向上的投影长度y.给出表达式如下：

因为θi和y均可表示成关于浮标吃水深度h的一元函数，所以在海水里的系泊系统的高度H也可表示成关于h的一元函数，H＝f（h）.

建立模型后，我们设定吃水深度h的一个初值，通过考虑整个系统在受力平衡状态下的情况，根据求解方程（1），（2），（3），得出各节钢管和钢桶间的拉力Ti及其与水平方向的夹角θi（i＝1，…，5）；再运用重物球的信息，求解方程（6），得出锚链和钢桶连接处的拉力T6及力与水平方向的夹角θ6.进而通过迭代算法得到锚链每节链环间（节点处）的相互作用力以及力与水平方向的夹角，由此建立平面坐标系确定各节点的横纵坐标，画出锚链的形状.

下一步，计算H的值并判断H的值是否满足条件如果满足条件，则给出满足条件时浮标吃水深度h的值；如果不满足条件，则不断通过修正浮标吃水深度h，求出满足条件时的吃水深度h值.

图6 高度H和半径R的示意图

其次，浮标的游动区域是一个以锚为中心的圆形区域，这个圆形区域的半径R可由海水里的系泊系统高度H模型的部分模型求得.将半径R看作两个部分长度的总和，分别是钢管和钢桶在水平方向上的投影长度L0以及锚链在竖直方向上的投影长度x，给出表达式如下：

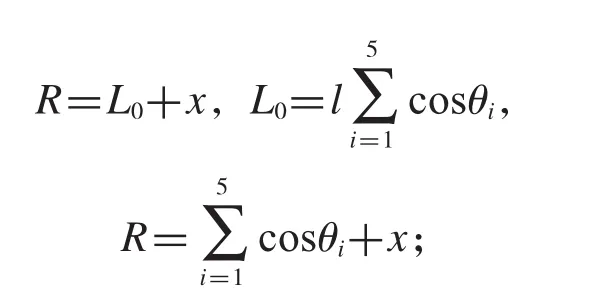
2.1.4 求解模型

先给吃水深度h设定一个初值，当海面风速v为12 m/s和24 m/s时，运用所建立的模型，分别求出海面风速为12 m/s和24 m/s时满足条件的吃水深度.利用所求出的吃水深度的值计算暴露在海面的浮标在风向法平面的投影面积以及浮标所受的浮力大小，再利用公式F＝0.625×Sv2（N）算出浮标受风的作用力（风荷载）的大小.然后将计算得出的值以及已知的数值代入方程（1），求出θ1.根据前面受力分析列出的方程推算出钢桶和各节钢管的倾斜角度.通过迭代算法并建立坐标系得出锚链形状.得到浮标的吃水深度后，根据系统受力平衡时浮标游动到离锚水平距离最长的地方，确定浮标的游动区域的半径R.

编写MATLAB程序[3]给出求解得到的结果见表1.

表1 满足条件的吃水深度

根据表1的值计算得出海面风速为12 m/s和24 m/s时的各节钢管和钢桶与水平方向的夹角θi值，见表2.

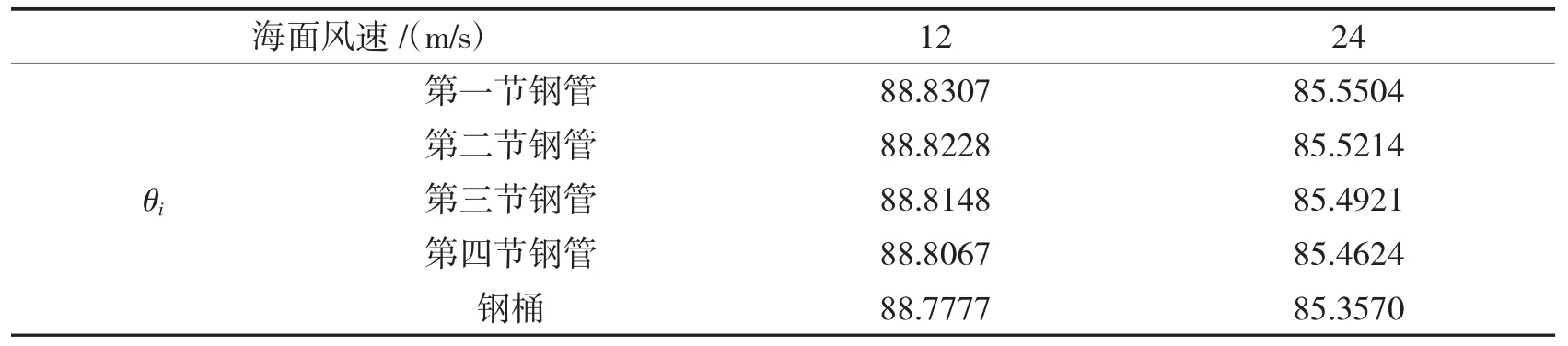
表2 各节钢管和钢桶与水平方向的夹角 （°）

各节钢管和钢桶的倾斜角度（与竖直方向的夹角）根据直角三角形内的两个锐角和等于90°算出，则海面风速分别为12 m/s和24 m/s时的各节钢管和钢桶的倾斜角度见表3.

得知浮标的吃水深度，求出T6和θ6后，通过迭代算法得到锚链每节链环间（节点处）的相互作用力以及力与水平方向的夹角，得到各节点的横纵坐标，由此建立坐标系，得出海面风速分别为12 m/s和24 m/s时锚链的形状.

图7 海面风速为12，24，36 m/s时的锚链形状

画出锚链形状图的同时我们给出起锚角的大小，见表4.

表4 海面风速为12 m/s和24 m/s时的起锚角

最后求出海面风速分别为12 m/s和24 m/s时浮标的游动区域半径R见表5.

表5 浮标的游动区域半径R

分析运用问题一模型所求解的全部结果，我们发现在钢桶与锚链连接处悬挂了1200 kg的重物球，海面风速为12 m/s和24 m/s时，起锚角分别为0°和0.1571°，均不超过16°；钢桶的倾斜角度分别为1.2223°和4.6430°，均不超过5°，虽然钢桶发生了倾斜但不处于竖直，所以系泊系统水声通讯设备的工作效果不处于较差状态.

2.2 问题二的分析

问题二需要先在问题一的假设下计算海面风速为36 m/s时钢桶和各节钢管的倾斜角度，锚链形状和浮标的游动区域，我们将运用问题一的模型计算出上述问题.然后问题需要调节重物球的质量，使得钢桶的倾斜角度不超过5°，锚链在锚点与海床的夹角（起锚角）不超过16°，据此我们判断海面风速为36 m/s时，钢桶倾斜角和起锚角偏大，致使系泊系统的水声通讯设备工作效果差.于是决定以1200 kg为调节重物球质量的初始值，选取质量范围为（1200，2600）kg进行调节，每隔100 kg取一个值分别计算出钢桶倾斜角和起锚角，得到范围内的一系列值后分别画出散点图，再通过二次拟合分别画出重物球质量-钢桶倾角及重物球质量-起锚角的函数关系图，最后得出符合题意的重物球质量.

2.2.1 求解海面风速为36 m/s时的系泊系统的情况

关于在问题一的假设下，计算海面风速为36 m/s时钢桶和各节钢管的倾斜角度，锚链形状和浮标的游动区域，我们运用模型一，解出当海面风速为36 m/s时浮标的吃水深度为0.7170米，然后就可计算出海面风速为36 m/s时钢桶和各节钢管的倾斜角，浮标的游动区域半径以及起锚角见表6，锚链形状见图7中的右图.

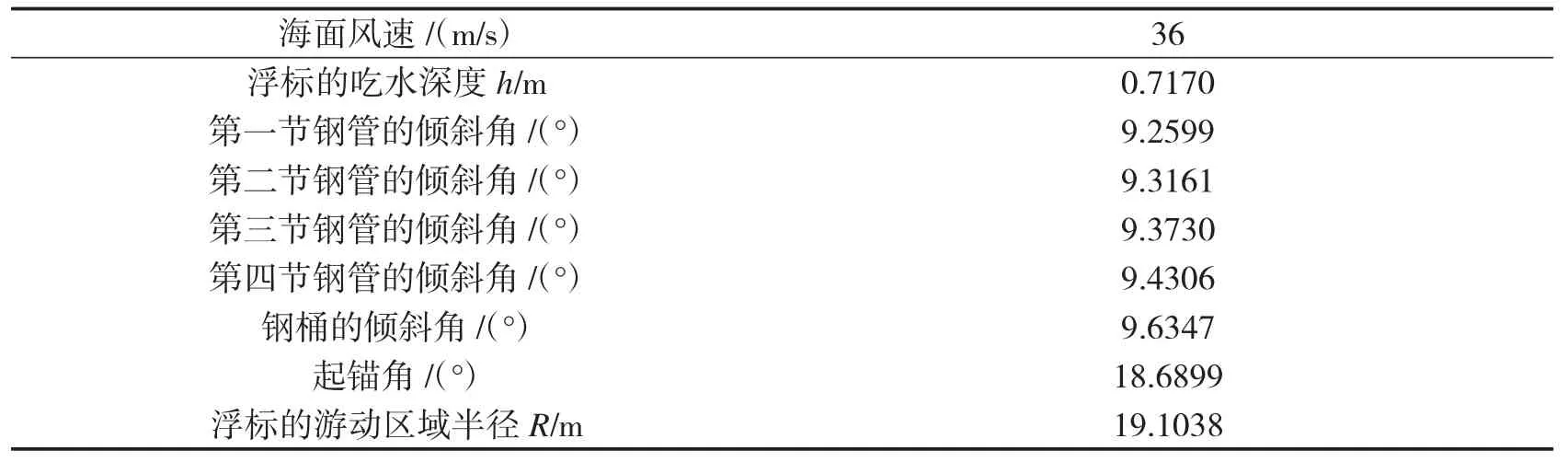
表6 海面风速为36m/s时系泊系统的基本情况数据

由表6中的数据我们得知，当选用的重物球质量为1200 kg，海面风速为36 m/s时，起锚角达到了18.6899°，超过16°；钢桶的倾斜角达到了9.6347°，超过5°，此时系泊系统水声通讯设备的工作效果差.

2.2.2 调节重物球的质量找出合适范围

得知海面风速为36 m/s时系泊系统的水声通讯设备的工作效果差后，我们打算给研究对象重物球质量设定一个调节范围，起始值为1200 kg，终止值为2600 kg.然后在范围（1200，2600）kg间，每隔100 kg取一个值并分别计算在该重物球质量下钢桶倾斜角和起锚角的大小.计算得到所选取范围内的一系列值后分别画出散点图，再通过二次拟合分别画出重物球质量-钢桶倾斜角以及重物球质量-起锚角的函数关系图.

下面给出在（1200，2600）kg范围区间所选取的重物球质量对应的钢桶倾斜角以及起锚角的数值表格7.

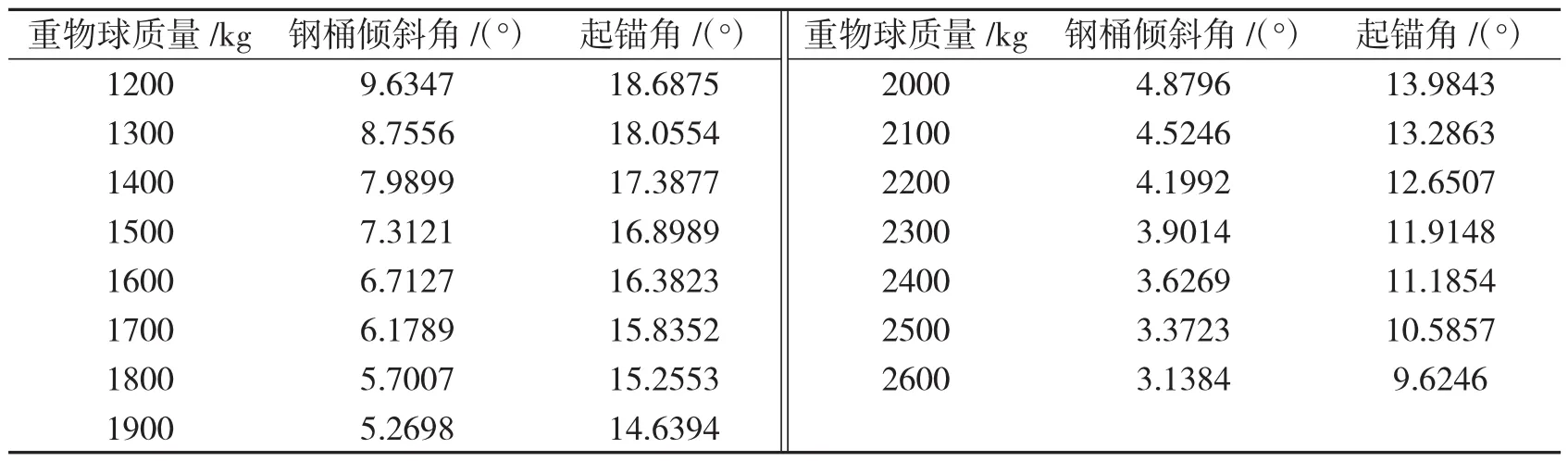
表7 各重物球质量对应的钢桶倾斜角以及起锚角

由表7可以得出，钢桶倾斜角为5°时对应的重物球质量在（1900，2000）kg范围内，起锚角为16°时对应的重物球质量在（1600，1700）kg范围内.因此可判断，要使钢桶倾斜角小于5°，起锚角小于16°同时满足，那么重物球质量的最小值应在（1900，2000）kg区间上.

再利用表7中的数值作出散点图，通过二次拟合分别作出重物球质量-钢桶倾斜角以及重物球质量-起锚角的函数关系图，并给出函数关系式，如图8所示.

图8 二次拟合后重物球质量-钢桶倾斜角、重物球质量-起锚角的函数关系图

给出图8二次拟合后的重物球质量（x）-钢桶倾斜角（y）函数关系式如下：

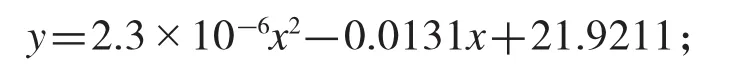
通过函数图像得知，要使钢桶的倾斜角度不超过5°，那么悬挂在钢桶上的重物球质量应该大于1963 kg.

图8二次拟合后的重物球质量（x）-起锚角（y）函数关系式如下：

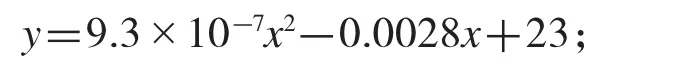
通过函数图像得知，要使起锚角的角度不超过16°，那么悬挂在钢桶上的重物球质量应该大于1668 kg.

综上，当海面风速为36 m/s时，要使得钢桶的倾斜角度不超过5°的同时，起锚角不超过16°，那么应调节重物球的质量大于1963 kg.

2.3 问题三的分析[4]

问题三中，重物球质量，锚链长度，水深，海水流动方向与风向夹角都是待定的变量，首先分析以上变量对要素（A）（B）（C）的影响.

（1）重物球质量：重物球主要影响该系统中的钢桶倾角及起锚角，可以运用问题二中的方法确定重物球的可取范围.

（2）水深与锚链长度：水深主要影响该系统中的锚链的长度.当水深增加，海平面升高时，如果锚链的长度不足，很容易造成起锚角过大，致使系泊系统发生起锚现象.因此可先考虑水深，风速，海水速度达到最大的时候，起锚角符合要求时的锚链长度.应用这个锚链长度值进行计算，以保证整个系统在潮汐涨落中保持稳定.

（3）海水流动方向与风向夹角：由于海水流动方向与风向夹角的存在，该系统的受力情况将由二维的转化为三维的，建立两个空间直角坐标系来表示该系统受到的力，将各个力分解到x轴，y轴，z轴上，以便于受力分析.再采用问题一中的模型解决（A）-（C）.

由此可见，重物球质量，水深，海水流动方向与风向夹角都会影响（A）-（C）.可采用控制变量法分不同情况研究三个变量对（A）-（C）的影响.

2.3.1 在空间直角坐标系下对浮标和钢管进行三维的物理受力分析

（1）类似问题一的受力分析，把浮标看作质点模型，以浮标质点为空间直角坐标系的原点，竖直方向为空间直角坐标系z轴方向，对浮标进行受力分析如图9所示.

由于在各力作用下，浮标处于受力平衡状态，将力分解到坐标轴上，我们得到如下方程：

整理简化方程后可得出如下表达式：

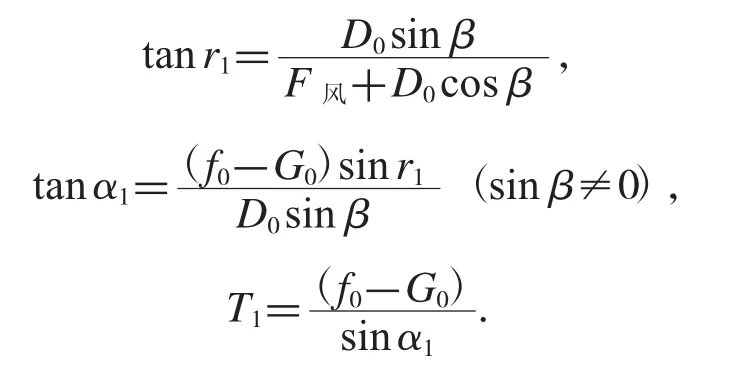
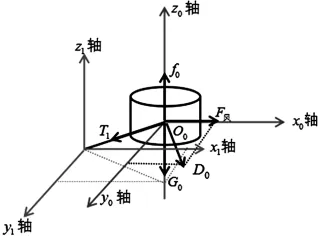
图9 浮标的三维受力分析图

图10 第一节钢管的三维受力分析图

（2）选取第一节钢管与浮标的连接点作为球坐标系的原点，采用质量集中法，把第一节钢管的质量集中在上方的连接点处，然后对第一节钢管进行三维的受力分析如图10所示.

同样地，在各个力的作用下第一节钢管上方的连接点处于受力平衡状态，将力都分解到坐标轴上，列出如下方程：

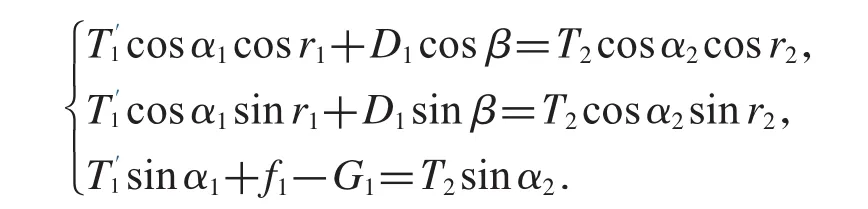
整理简化方程后得出如下表达式：

（3）与处理第一节钢管类似地分别处理第二，第三，第四节钢管，然后也可给出相应的三维受力分析图，并列出受力平衡状态下的通用方程如下，其中i＝3，4，5：

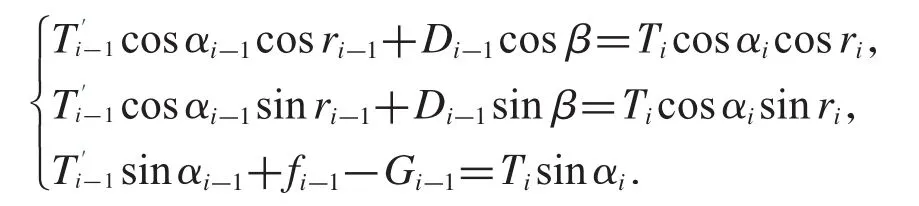
整理简化方程后亦可得下述通用方程式：

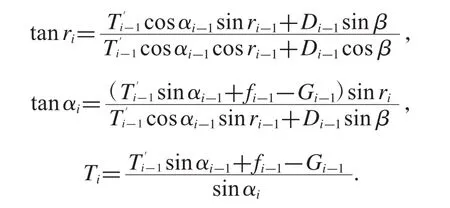
（4）根据整体法，将钢桶和重物球看作一个整体，并视为质点模型，然后进行受力分析，得出受力分析图11.

将各个力分解到坐标轴上，给出平衡状态下的方程如下.

图11 钢桶和重物球整体的三维受力分析图

2.3.2 采用控制变量法，研究变量为锚链型号时的情况

受力分析后我们建立单点系泊系统三维静力学模型，然后运用以上所建模型，控制重物球质量为4300 kg，锚链节数为300节，海面风速为36 m/s，海水速度为1.5 m/s，研究不同锚链型号对吃水深度、各钢管以及钢桶的倾角和起锚角的影响，得到表8.

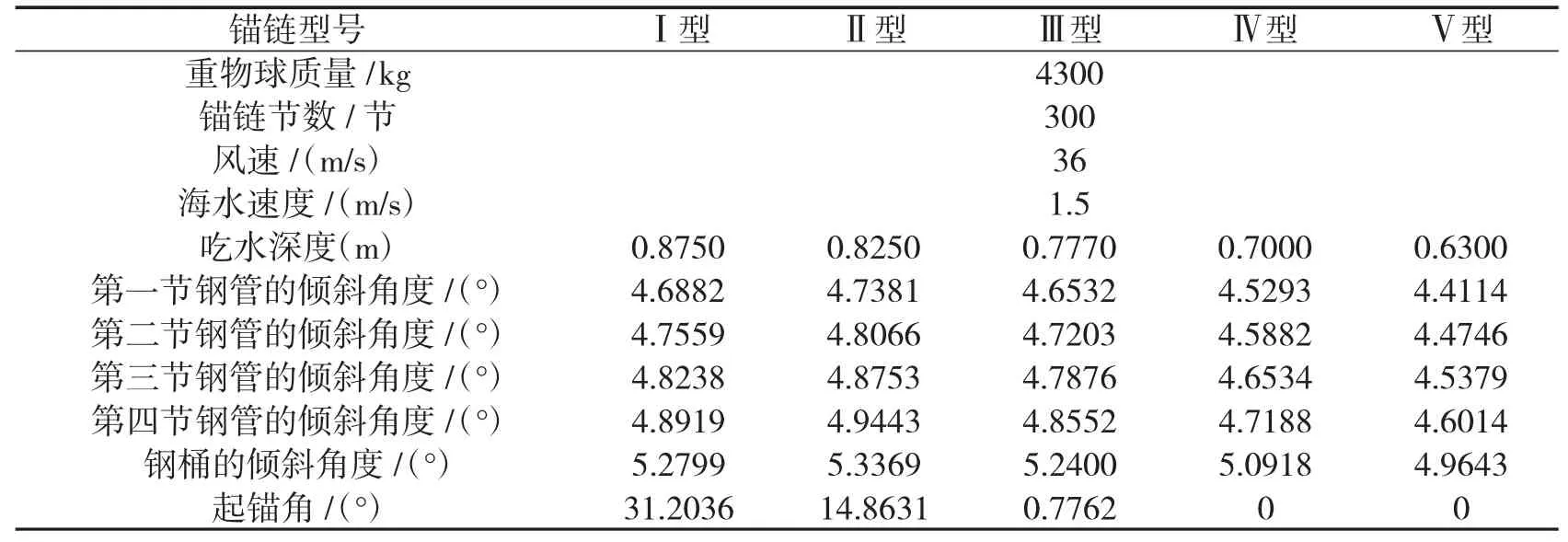
表8 控制变量为锚链型号时系泊系统的情况

由表8可以看出：同样的重物球质量，锚链节数，风速，海水速度下，Ⅰ型锚链会造成系统的起锚角过大，使用Ⅱ型，Ⅲ型锚链可以得到正常起锚角，使用Ⅳ型，Ⅴ型锚链，系泊系统中会有一部分的锚链躺在地上，但Ⅴ型通讯设备工作效果最佳.

依据上述结果，同样的重物球质量，锚链节数，风速，海水速度下，系泊系统在分别使用Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅴ型锚链时，稳定性一次增强，但造价依次上升，故因综合考虑稳定性和造价选择锚链型号.

3 总结

本文通过建立单点系泊系统二维静力学模型完整地解决了问题一和问题二.对于问题一，建立二维静力学模型，选定吃水深度的一个初值，然后根据所给出的解决问题一的流程图不断检验，最终得到符合题意的吃水深度的确定值，再逐步确定系泊系统各个部位的倾斜角等参数；对于锚链形状，采用悬链线方程和迭代法；对于问题二，在问题一中模型基础上，用二次拟合求出当风速改变时，得出工作状态最佳的最小重物球质量；而针对问题三，二维静力学模型已不足以用来解决问题，需将二维转化为三维，应用三维静力学模型在不同情况下系泊系统各部位状态的影响.

[1]袁梦，范菊，缪国平，等.系泊系统动力分析[J].水动力学研究与进展（A辑），2010，25（3）：285-291.

[2]王磊.单点系泊系统的动力学研究[D].青岛：中国海洋大学，2012.

[3]卓金武，李必文，魏永生，等.MATLAB在数学建模中的应用[M].北京：北京航空航天大学出版社，2014.

[4]李晓平.多体系统动力学建模方法及在水下缆索中的应用研究[D].天津：天津大学，2004.