基于互信息与贝叶斯信念网络的关系层次距离混合聚类算法

蔡金成，孙浩军

（汕头大学工学院，广东 汕头 515063）

0 引言

聚类被广泛应用于计算数据之间的相似性并通过其相似性将数据区分和分类，期间被划分在同一组的数据相似性强，而划分在不同组之间的数据相似性弱，这是一种没有先验知识指导的分类过程，属于无监督的分类[1-2].在聚类中，很多算法只针对单一的分类型属性[3-4]或者单一的数值性属性[5-6]，然而数据在实际应用中不仅包含数值型属性，同时包括类似颜色、几何纹理等分类型属性，而针对这种混合型数据的算法很少，主要原因是难以精确度量分类型数据之间的相似性.对于度量分类型数据相似性也有一些算法，但都存在着局限性与不足，如在文献[7]中，通过将分类型数据转换成为二进制数值，然后利用简单的距离度量（如，欧氏距离等），并结合数值型属性，统一按照数值型属性进行聚类.然而在很多情况下会导致分类型属性语义的丢失.另一些研究者通过对分类型数据进行概念分层[2]，以及在分层附上距离形成层次距离[8]来度量分类型数据之间的相似性[9].然而，概念分层需要专业的领域知识来分层，而且很多情况下分类型数据并没有层次的概念（如，颜色、图案等）.

这里我们提出一种基于互信息与贝叶斯信念网络的方法来度量分类型数据之间的相似性，并结合标准化的曼哈顿距离来度量数值型数据的相似性，设计用于混合型数据的聚类算法，其主要思路是，对于分类型属性，利用互信息构建贝叶斯信念网络，利用贝叶斯信念网络构建关系层次，继而为层次附上距离，形成关系层次距离，而对于数值型属性则利用标准化的曼哈顿距离来度量其相似性，最后结合分类型属性与数值型属性来对整个数据集进行相似性的度量，利用相似性聚类.我们通过UCI中的多个数据集进行仿真实验，可以得到较好的聚类效果.

文章第1章介绍相关概念，包括互信息、贝叶斯信念网络、关系层次距离的相关概念；第2章是本文算法的过程描述，包括构建贝叶斯信念网络、关系层次距离、聚类过程；第3章是实验及结果情况；最后总结本文.

1 相关概念

1.1 互信息

在概率论中，两个随机变量的互信息（Mutual Information）是变量间相互依赖性的量度.对于两个随机变量X与Y之间的互信息定义为I（X；Y），在数学上定义为：

其中H（X）是随机变量X的信息熵，是给定随机变量Y，X的条件信息熵.随机变量的信息熵和条件信息熵在数学上分别定义为：

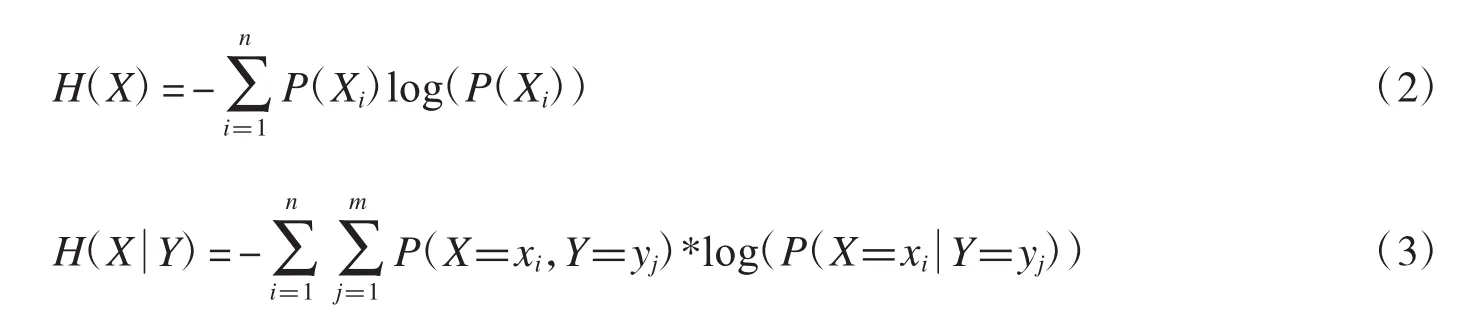
在以上两个式子中，n和m分别是随机变量X和Y的离散状态的数量；P（X＝xi，Y＝yj）则是随机变量X和Y的联合概率分布；随机变量X和Y的互信息是对称的，数学上表示为：I（X；Y）＝I（Y；X）.

两个随机变量X与Y的标准互信息（Normalized Mutual Information）定义为NMI（X；Y），其数学上定义为：

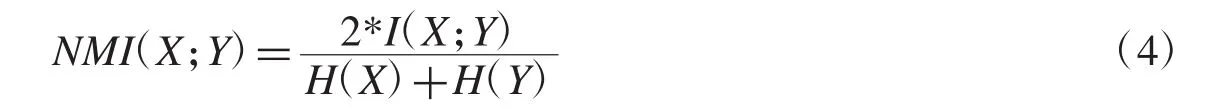
随机变量的标准互信息是对随机变量的互信息的归一化.随机变量的互信息既可以表示为（1）式，同时由于其对称性，也可以表示为 I（X；Y）＝H（X）+H（Y）-H（X，Y）.因此，当X与Y完全一样时，I（X；Y）取得最大值为1，此时，H（X）＝H（Y）且其值为1，H（X，Y）值为 0，则 NMI（X；Y）取得最大值为 1.当 X 与 Y 完全不一样时，I（X；Y）取得最小值为0，则NMI（X；Y）取得最小值为0，综上所述NMI（X；Y）的取值范围为[0，1].

1.2 贝叶斯信念网络

贝叶斯信念网络（Bayesian Belief Network）借助有向无环图（Directed Acyclic graph，简称DAG）来描述属性之间的依赖关系，并使用条件概率表（Conditional Probability Table，简称CPT）来描述属性的联合概率分布[10].

具体来说，一个贝叶斯信念网络B由结构G和参数θ两部分构成，即B＝＜G，θ＞，结构G是一个有向无环图，每一个节点对应一个属性，若两个属性有着直接的依赖关系，则它们由一条边连接起来；参数θ定量描述了这种依赖关系.假设属性ai在G中的父节点集为则θ包含了每个属性的条件概率表下面我们就UCI中的diagnosis数据集[12]通过标准互信息构建贝叶斯网络[13]，如图1所示，其中TP属性的四个状态（P、W、G、N）是离散化的结果.

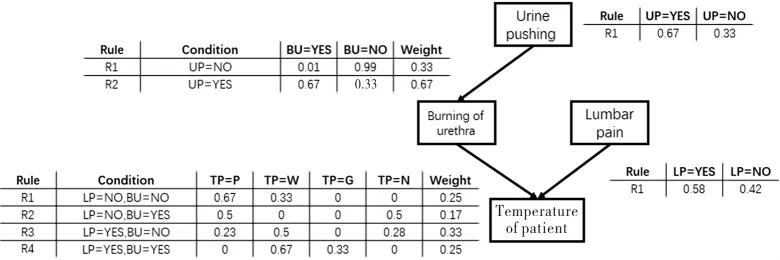
图1 基于标准互信息构建的diagnosis数据集的信念网络

1.3 关系层次距离

层次距离[8]是在概念分层[2]的基础上扩展的，层次距离与概念分层相似，都是通过概念将不同的物体抽象成不同的层次，每个物体就是一个结点，并且通过边连接起来.层次越高则物体的概念更加抽象，层次越底物体的概念越具体.此外，每个结点连接的边都用一个权值表示距离.本文提出一种关系层次距离来度量分类型属性之间的距离，即通过标准互信息构建贝叶斯信念网络，再通过贝叶斯信念网络构建关系层次结构，并对关系层次附上距离.图2（属性Urine pushing），图3（属性Lumbar pain），图4（属性Burning of urethra），图5（属性Temperature of patient）分别为图1中每个属性不同状态的概率层次结构，而对于关系层次距离的定义分为多种情况，具体如下.

（1）如果所有结点间都只由一条规则（Rule）所影响，则该规则所影响的结点之间的关系距离定义为：

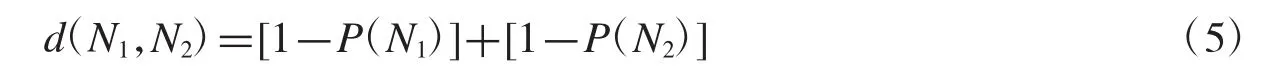
其中，N1表示结点，P（N1）表示在贝叶斯信念网络中形成的概率表中在规则的影响下的结点N1概率，如图2和图3.其中图2中两个结点之间的距离为：d2（N1，N2）＝（1-0.67）+（1-0.33）＝1

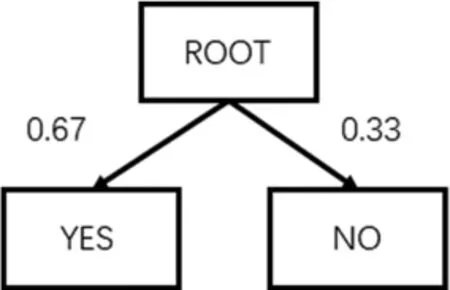
图2 属性UP的概率表组成的层次结构图

图3 属性LP的概率表组成的层次结构图

（2）如果结点与结点间存在多条规则且每条规则都影响着属性的所有状态，则需要根据规则的影响能力来计算结点间的距离，并且按照路径最短距离来计算（即计算路径不需要经过ROOT），

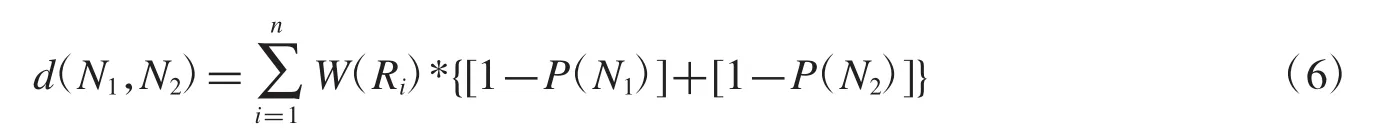
W（Ri）表示第i条规则的权重.如图4，两个结点之间的距离为：d4（N1，N2）＝0.33*{[1-0.01]+[1-0.99]}+0.67*{[1-0.67]+[1-0.33]}＝1.

（3）如果结点与结点间存在多条规则且某些规则只影响了部分结点，则对于结点与结点之间的距离定义如下：

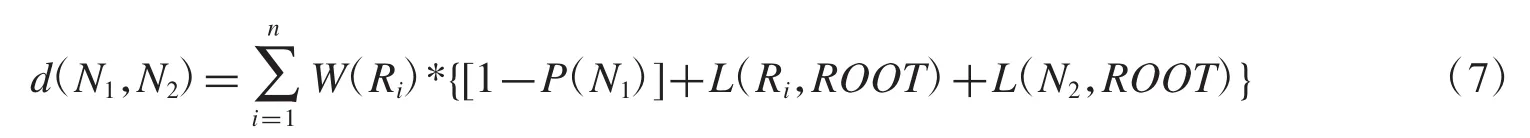
W（Ri）表示第i条规则的权重；L（Ri，ROOT）表示结点N1所在的第i条规则到Root的层数，每层值为1；L（N2，ROOT）表示不受规则i所影响的结点N2到Root的层数，每层值为1.如图5，两个结点之间的距离为：d5（P，G）＝0.25*{[1-0.67]+1+2}+0.17*{[1-0.23]+1+2}+0.33*{[1-0.50]+1+2}+0.25*{[1-0.33]+1+2}＝3.55

图4 属性BU的概率表组成的层次结构图

图5 属性TP的概率表组成的层次结构图

1.4 代价函数

代价函数表示的是对象间的相似程度.本文算法CRHD是混合聚类算法，因此是包含数值型属性和分类型属性的混合代价函数.

假设 X＝{X1，X2，…，XN}是包含 N 个数据元素的数据集；Xi＝{Xi1，Xi2，…，XiD}是一个包含D维的数据元素；Xnr是随机变量的第r个数值型属性，r＝1，…，p；Xcs是随机变量的第s个分类型属性，s＝1，…，q，并且p+q＝D.我们将数据集X分割成K个不相交的簇中，形成C1，…，Ck，其中K是提前先给定的.

定义1两个向量的数值型属性之间的标准化曼哈顿距离的度量如下：

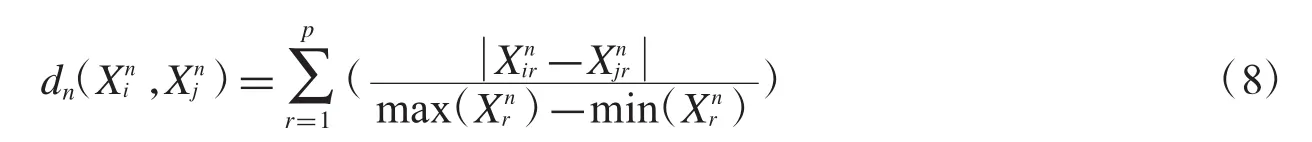
其中表示第i个数据元素的第r个数值型属性的值，n表示数值型数据；表示数据集的第r个数值型属性中的最大值.

定义2分类型数据在同一个属性中的两种不同状态之间的距离的度量如下：

式子（9-1）的使用条件是所有结点间都只由一条规则所影响；式子（9-2）的使用条件是结点与结点间存在多条规则且每条规则都影响着属性的所有状态；式子（9-3）的使用条件是结点与结点间存在多条规则且某些规则只影响了部分结点.其中P（N1）、P（N2）表示在某条规则影响下的概率；W（Ri）表示第i条规则的权重；L（Ri，ROOT）表示第i条规则到ROOT的层数，每层距离值为1；L（N2，ROOT）表示结点N2到ROOT的层数，每层距离值为1.

定义3两个向量的分类型属性之间的标准化关系层次距离度量如下：

其中max（d（Nis，Njs））表示在数据集的第s个属性中不同状态两两之间的距离的最大值；d（Nis，Njs）见公式（9）中的定义.

定义4两个向量间的距离度量如下：

2 关系层次距离聚类算法（CRHD）

利用互信息构建贝叶斯信念网络度量分类型数据之间的相似性，利用标准化的曼哈顿距离来度量数值型数据的相似性，通过这两种相似度的计算来设计用于混合型数据的聚类算法：关系层次距离聚类算法Clustering for Relation Hierarchies Distance（简称CRHD）.CRHD对于分类型属性的计算是通过标准互信息计算属性的相关性来构建贝叶斯信念网络，并利用贝叶斯信念网络构建关系层次距离，通过构建关系层次距离来度量分类型属性中各个状态之间的距离，再根据公式（10）进行标准化处理，而对于数值型数据则采用标准化的曼哈顿距离进行度量其距离（公式8），最后结合分类型属性与数值型属性的距离度量方法（公式11）对整个数据集进行聚类.

2.1 构建贝叶斯信念网络

贝叶斯信念网络借助有向无环图来描述属性之间的依赖关系，使用条件概率表来描述属性的联合概率分布.贝叶斯信念网络构建的主要步骤是构建无向图，再通过剪枝形成无环图，最后指派方向，其基本步骤如下：

1）利用标准互信息来度量分类型属性之间的相关性程度；

2）对相关性程度在阈值范围内的属性用边连接起来，形成无向图；

3）对存在三角环的属性利用维分割[14]和条件概率进行剪枝，形成无环连通图或存在大于三结点的有环连通图；

4）通过条件概率、K2算法分数评估[13]，再进行方向的指派，形成有向无环图.

2.2 关系层次距离的计算

对于关系层次距离的定义，不同属性有着不同的定义方式，主要跟属性与属性之间的关系有关，其主要的计算步骤如下：

（1）对于每个属性都有贝叶斯信念网络计算出来的概率表，包括规则对应的概率表、规则的权重；

（2）根据公式（9）进行计算各个属性中状态的距离，作为状态间的相似度度量；

（3）根据公式（10）对分类型属性的距离进行度量.

2.3 聚类算法描述

关系层次距离聚类算法通过标准互信息对贝叶斯网络的构建，并利用其相关性构建关系层次距离，再利用关系层次距离对分类型属性进行相似度计算并做标准化处理，最后结合数值型数据的标准化曼哈顿距离的度量进行聚类.聚类的过程分成两个阶段：阶段一，是通过数据相似性计算聚类中心点；阶段二，是将剩余元素指派到子簇中心点的过程.

输入：数据集 X＝{X1，X2，…，XN}，簇个数 K

输出：聚类结果 C＝{C1，C2，…CK}

阶段一得到聚类中心点算法：

Step0：利用公式（8）、（9）、（10）计算数据集X中数据两两之间的距离矩阵；

Step1：按比例从数据集X中随机选择样本，记录其下标保存在S中；

Step2：从距离矩阵中距离最大的值对应的两个样本下标，记为p1及p2；

Step3：将p1及p2插入到result中，从S中删除这两个下标，并记k＝2；

Step3：while K＞k：

Step3-0：得到S中剩下的所有样本与p1p2的距离矩阵；

Step3-1：从step3-0得到S中未分配的每个样本，分别取与p1p2的最小距离的值；

Step3-2：从step3-1中所有距离最小的值中选取距离最大的值，并得到其下标，记为Pcount；

Step3-3：从X中删除Pcount，并将Pcount作为第k个子簇的中心点，k＝k+1；

阶段二迭代剩下数据算法：

Step1：获取已指派样本的下标，result保存当前k个子簇的下标；

Step2：获取剩余的还没被指派的下标列表remainder；

Step3：对于每个 remainder里面的每个样本，利用公式（8）（9）（10）（11）计算它与当前每个子簇的相似度；

Step4：将每个remainder里面的每个样本逐一分配给与当前子簇相似度最大的簇中；

3 实验及结果

3.1 实验数据

实验数据采用UCI机器学习库[15]中的两个数据集（diagnosis、covType）做为实验数据，表1是数据集的详细描述，数据库中有它们自己的分类，用于最后评价聚类的性能的参考.

表1 两个实验数据集

3.2 评估函数

对于本文的聚类效果评估采用AC和ARI评估函数进行评估，具体如下：

（1）Accuracy（简称 AC）

其中是数据集X的数据个数，K是测试数据集的类的个数，是表示第i的类中属于同一类的对象最多的数据个数.

（2）Adjusted Rand index（简称 ARI）

给定 n 个对象的数据集，假设 U＝{u1，u2，…，us}和 V＝{v1，v2，…，vt}分别表示数据集的原始类分布以及算法聚类结果分布，nij表示同时在类ui和簇vi，然后Ui和Vi分别表示在类ui和类vi数据对象个数，则ARI计算如下：

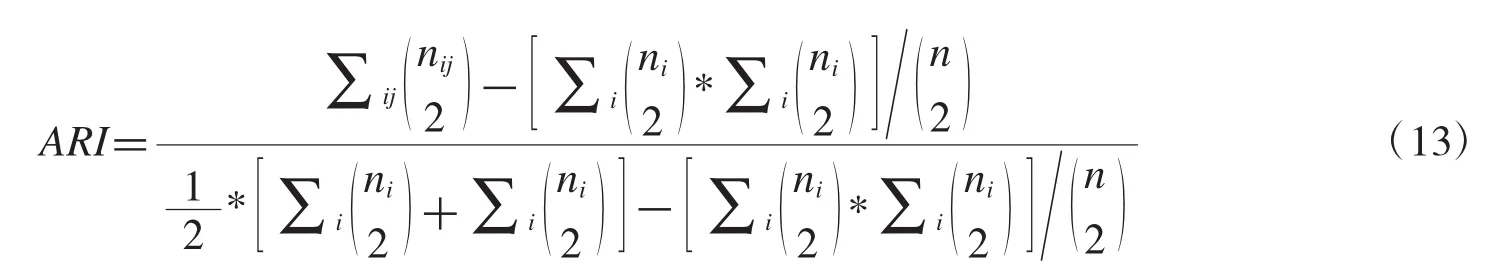
3.3 结果及分析

下面分析CRHD算法在上述UCI的两个数据集（diagnosis、covType）的实验结果.表2中得出了CRHD算法在数据集diagnosis中的准确率AC和ARI的值指标.三个算法的准确率AC和ARI的指标如表3和表4所示.

数据集diagnosis包含了120个数据对象，有两个类，域值都为{YES、NO}，即该数据集的分类阈值有四个{（NO、NO）、（NO、YES）、（YES、NO）、（YES、YES）}.如表2所示，CRHD可以在类（NO、NO）、（YES、YES）获得比较好的结果.在其他两个类分值也有较好的结果，其准确度AC为0.8333，ARI值为0.6341.

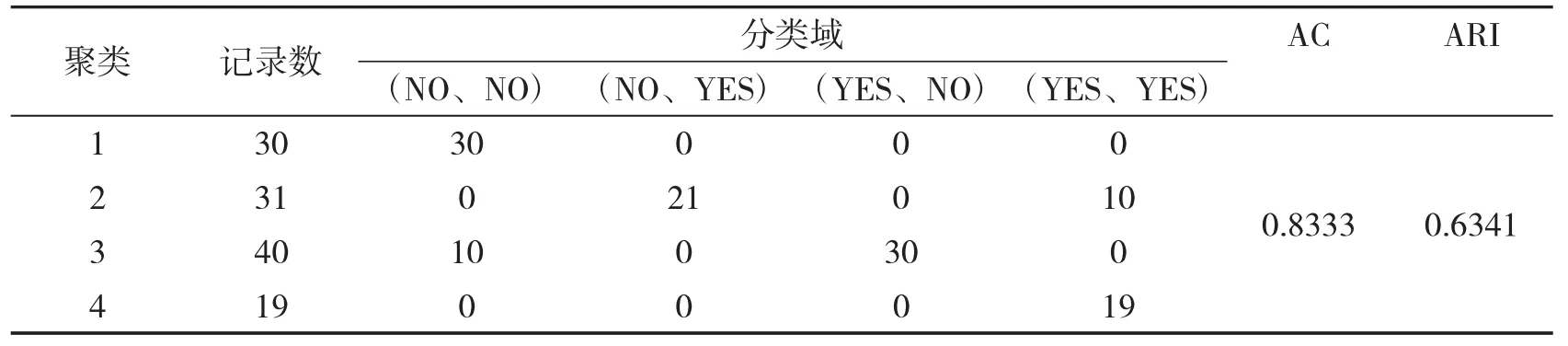
表2 CRHD算法在数据diagnosis上的实验结果

如表3和表4可以看出通过三种算法对两个数据（其中covType按比例选取1 645个数据）进行试验.CRHD算法在两个数据集的ARI评估上优于其他两种（K-prototype、ROCK）算法，在数据集diagnosis上CRHD算法的AC准确率评估优于其他两种算法，但在数据集covType上算法ROCK准确率AC优于其他算法，总而言之，本文提出的CRHD算法能够获得较好的效率和准确率.但是本算法CRHD也存在两点不足：其一，CRHD算法在构建贝叶斯网络时存在局限性，贝叶斯网络的构建要求属性之间存在相关性；其二，在高维数据集中构建贝叶斯信念网络也存在较高的难度.

表3 评估函数AC对三个算法在两个数据上的聚类结果评估的结果

表4 评估函数ARI对三个算法在两个数据上的聚类结果评估的结果

4 结束语

在传统的聚类算法中大多都仅限于处理数值型数据或者分类型数据.即使存在一些聚类算法是对混合型数据进行聚类的，但是也存在诸多缺点，如不能保留分类型属性本身的含义同时在处理过程也消耗大量内存或者需要专业领域知识进行概念分层附上层次距离等.本文CRHD算法通过计算属性之间的互信息来构建贝叶斯信念网络，通过贝叶斯信念网络来构建关系层次结构并附上距离来度量属性中各个状态的相似性，从而解决了以上提到的混合聚类算法中存在的缺点.最后通过采用UCI中的数据集进行试验，结果利用AC和ARI准确率评估算法进行评估，评估结果较有效，证明了本文CRHD算法的广泛性和有效性.

[1]DUNHAM M H.Data mining-introductory and advanced topics[M].New Jersey：Prentice-Hall，2003.

[2]HAN J，KAMBER M.Data mining concepts and techniques[M].San Francisco：Morgan Kaufmann，2001.

[3]BARBARA D，COUTO J，LI Y.COOLCAT：An entropy-based algorithm for categorical clustering[C/OL].Proceedings of the Eleventh International Conference on Information and Knowledge Management.2002：582-589[2018-02-20].https://cs.gmu.edu/～dbarbara/COOLCAT/coolcat.pdf

[4]GANTIV，GEHRKE J，RAMAKRISHNAN R.CACTUS clustering categorical data using summaries[C/OL].Proceedings of the ACMSIGKDD，International Conference on Knowledge Discovery and Data Mining，1999：113-120[2018-02-20].http://www.cs.cornell.edu/johannes/papers/1999/kdd1999-cactus.pdf

[5]JAINAK，DUBES R C.Algorithms for clustering data Englewood Cliffs[M].New Jersey： Prentice-Hall，1988.

[6]MACQUEEN J B.Some methods for classification and analysis of multivariate observations[C/OL].Proceedings of the 5th Berkeley Ymposium on Mathematical Statistics and Probability 1967：281-297[2018-02-20].http://citeseer.ist.psu.edu/viewdoc/download；jsessionid=E20C2D397F6BD55732573CDD 9C33575A?doi=10.1.1.308.8619&rep=rep1&type=pdf

[7]GUHA S，RASTOGI R，SHIM K.ROCK：A robust clustering algorithm for categorical attributes[C/OL].Proceedings of the 15thInternational Conference on Data Engineering.1999[2018-02-20].http://theory.stanford.edu/～sudipto/mypapers/categorical.pdf

[8]HSUCC.Generalizing self-organizing map for categorical data[J].IEEE Transactions on NeuralNetworks，2006，17（2）：294-304.

[9]HSU C C，CHEN Y C.Mining of mixed data with application to catalog marketing[J].Expert Systems with Applications，2007，32（1）：12-23.

[10]JENSEN F.An introduction to bayesian networks[M].London：UCL Press，1996.

[11]周志华.机器学习[M].北京：清华大学出版社，2016.

[12]UC irvine machine learning repository[DB/OL].[2018-02-20].http://archive.ics.uci.edu/ml/datasets/Acute+Inflammations

[13]CHEN X W，ANANTHA G，LIN X.Improving bayesian network structure learning with mutual information-based node ordering in the K2 Algorithm[J].IEEE Transactions on Knowledge&Data Engineering，2008，20（5）：628-640.

[14]BUTZ C J，YAN W，MADSEN A L.d-Separation：strong completeness of semantics in bayesian network inference[M]//Advances in Artificial Intelligence.Springer Berlin Heidelberg，2013：13-24.

[15]UC Irvine Machine Learning Repository[DB/OL].[2018-02-20].http://archive.ics.uci.edu/ml/index.php