Hilbert空间中g-R-对偶的一些性质

庞桥森，杨守志

（汕头大学数学系，广东 汕头 515063）

0 引言

Hilbert空间中的框架概念由Duffin和Schaeffer[1]在研究非调和Fourier级数时提出.之后很多学者对其做了广泛的研究，使得框架理论应用于信号处理，信号采样，图像处理，系统模型等诸多领域，随着对框架理论研究的不断深入，许多学者对框架理论进行了各种推广，孙文昌教授[2]首先提出了一种更为一般的框架概念即g-框架，并对g-框架的性质进行了一些研究.为了在Gabor分析中得到更具一般性的对偶原则，Casazza，Kutyniook和Lammers[3]于2004年首次提出了框架的R-对偶（第一类R-对偶）的概念，并讨论了框架R-对偶的一些性质.之后Christensen[4]于2015年提出了第二类R-对偶、第三类R-对偶、第四类R-对偶的概念，进一步丰富了框架的R-对偶的内容.

在文献[5]中，Osgooei和Najati首先把R-对偶的内容推广到g-框架，并研究了Hilbert空间上g-框架的第一类g-R-对偶的某些性质.在文献[6]中，Khosravi和Takhteh又把第二类R-对偶、第三类R-对偶、第四类R-对偶的概念推广到g-框架上，同样也讨论了这三类R-对偶在g-框架上的一些性质，并且根据第一类g-R-对偶，给出了对偶g-框架的一个刻画.本文在此基础上，讨论了g-框架上第一类g-R-对偶的一些新的性质，并且根据第三类g-R-对偶给出对偶g-框架的一个刻画.

在本文中，H是复的可分Hilbert空间，其内积为＜·，·＞，I是整数集的子集，{Hi}i∈I是H的闭子空间序列，B（H，Hi）表示H到Hi的所有有界线性算子的全体.

1 预备知识

定义1序列Λ＝{Λi∈B（H，Hi）:i∈I}称为Hilbert空间H关于{Hi}i∈I的g-框架，如果存在A，B＞0，对任意的f∈H有

成立，称A，B分别为g-框架的下界和上界.

若仅有右边不等式成立，则称Λ是界为B的g-Bessel序列.

若A＝B，则称为紧g-框架.若A＝B＝1，则称为g-Parseval框架.

如果{Λi}i∈I是的一个g-框架，则称为g-框架序列.

定义线性空间：

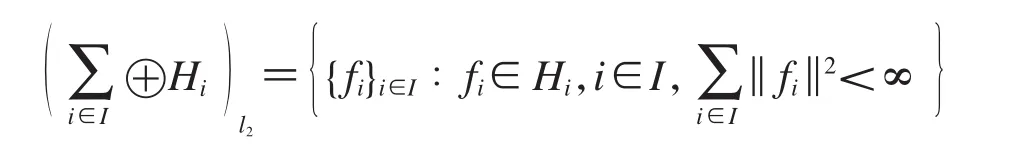
和内积〈·，·〉

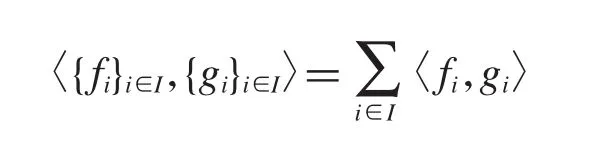
则是一个Hilbert空间.

如果Λ＝{Λi}i∈I是一个g-Bessel序列，那么Λ的合成算子为

它的共轭算子，即分析算子为

g-Bessel序列 Λ＝{Λi}i∈I的框架算子 SΛ定义为：

因此有如果Λ＝{Λi}i∈I是H的一个界为A，B的g-框架，那么g-框架算子SΛ是有界的，自伴的且可逆的.它的典范对偶定义为其中也是 H 的一个g-框架，框架界为B-1，A-1，并且

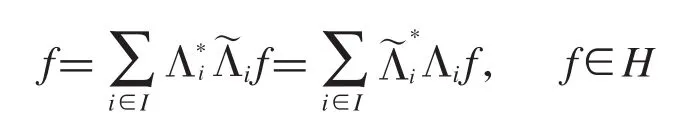
定义 2 设 Λ＝{Λi}i∈I和 Θ＝{Θi}i∈I是 H 关于{Hi}i∈I的两个 g-Bessel序列，如果

成立，则称Λ和Θ互为对偶g-框架.

定义3 序列Λ＝{Λi}i∈I称为Hilbert空间H关于{Hi}i∈I的g-标准正交基，如果满足下列两个条件：

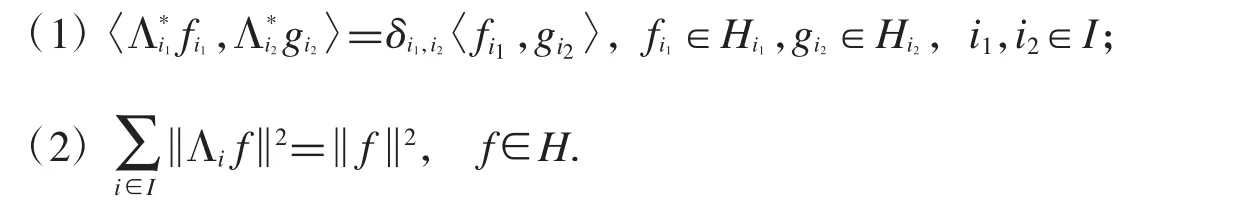
定义4 序列Λ＝{Λi}i∈I称为Hilbert空间H关于{Hi}i∈I的g-Riesz基，如果满足下列两个条件：

（1）{Λi}i∈I是 g-完备的，即{f∈H:Λif＝0，i∈I}＝{0}；

（2）存在正数A，B使得对任意有限集合I1∈I和任意gi∈Hi，i1∈I1有

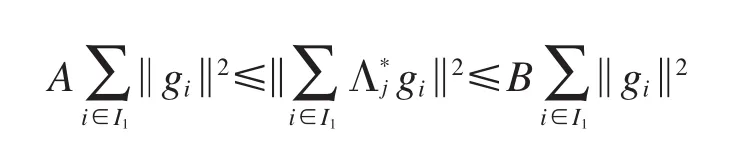
注1如果{Λi}i∈I是一组g-标准正交基，那么根据定义有

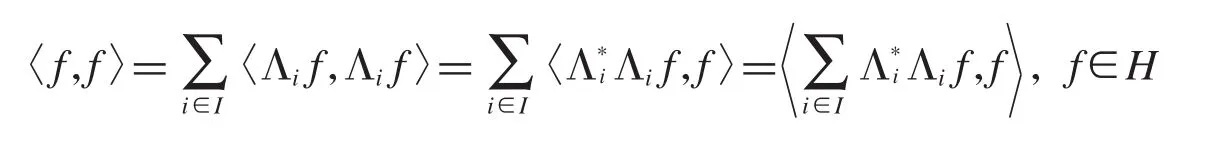
则有

设Λ＝{Λi∈B（H，Hi）:i∈I}和Θ＝{Θi∈B（H，Hi）:i∈I}是g-Bessel界为B，C的两个g-Bessel序列，定义算子：

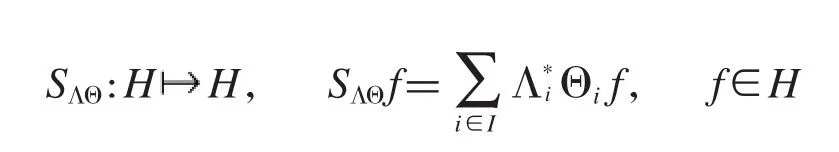
那么根据文献[8]有特别地

定义5[6]设Λ＝{Λi∈B（H，Hi）:i∈I}是H的一个g-框架，S为g-框架算子.

（1）令Γ＝{Γi∈B（H，Hi）:i∈I}和Υ＝{Υi∈B（H，Hi）:i∈I}是g-标准正交基，Λ与（Γ，Υ）相关的第一类 g-R-对偶是其中

（2）令Γ＝{Γi∈B（H，Hi）:i∈I}和Υ＝{Υi∈B（H，Hi）:i∈I}是g-标准正交基，Λ与（Γ，Υ）相关的第二类 g-R-对偶是其中

（3）令是g-标准正交基，M:HH是一个满足的有界可逆算子，Λ与（Γ，Υ，M）相关的第三类g-R-对偶是其中

（4）令是g-Riesz基，Λ与（Γ，Υ）相关的第四类 g-R-对偶是其中

注2在第三类g-R-对偶中，M的选择有无穷多种.显然是成立的，那么也成立，其中U为任意酉算子.

定义6[7]设Λ和Θ是H的两个g-框架

（1）如果存在一个有界线性可逆算子T:HH，使得Θi＝ΛiT，∀i∈I，则称Λ和Θ相似.

（2）如果存在一个酉线性算子T:HH，使得Θi＝ΛiT，∀i∈I，则称Λ和Θ酉等价.

引理1[7]设Λ和Θ是H的两个g-框架，那么当且仅当Λ和Θ相似.

引理 2[5]设 Λ＝{Λi}i∈I为 Hilbert空间 H 关于{Hi}i∈I的 g-Bessel序列，表示Λ 的第一类 g-R-对偶，那么对所有的有

其中

引理 3[5]设 Λ＝{Λi}i∈I为 Hilbert空间 H 关于{Hi}i∈I的 g-Bessel序列表示 Λ 与g-标准正交基 Γ＝{Γi}i∈I和 Υ＝{Υi}i∈I相关的第一类 g-R-对偶，对有下列结论成立：

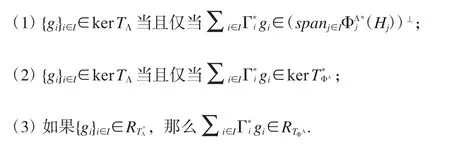
引理4[6]设Λ＝{Λi∈B（H，HI）:i∈I}是H的一个g-框架序列，其g-框架算子为S，Γ＝{Γi∈B（H，HI）:i∈I}和 Υ＝{Υi∈B（H，HI）:i∈I}是 g-标准正交基，是 Λ 与（Γ，Υ）相关的第一类g-R-对偶，那么下面两个结论等价：

（1）Θ是Λ的一个对偶g-框架；

（2）存在一个g-Bessel序列使得对每个gj∈Hj，j∈I都有

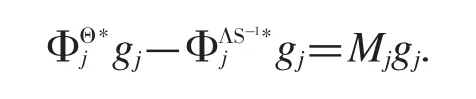
2 主要结论

在这部分，首先给出第一类g-R-对偶的几个性质，最后再根据第三类g-R-对偶给出对偶g-框架的一个刻画.

性质1 如果 Λ＝{Λi}i∈I是Hilbert空间H关于{Hi}i∈I的g-Bessel序列，Λ 的g-框架算子为表示 Λ 与 g-标准正交基 Γ＝{Γi}i∈I和 Υ＝{Υi}i∈I相关的第一类 g-R-对偶，则有

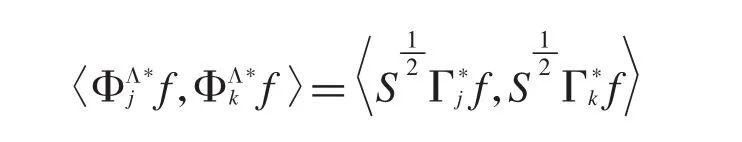
特别地，即酉等价.

证明：根据第一类g-R-对偶和g-标准正交基的定义，有

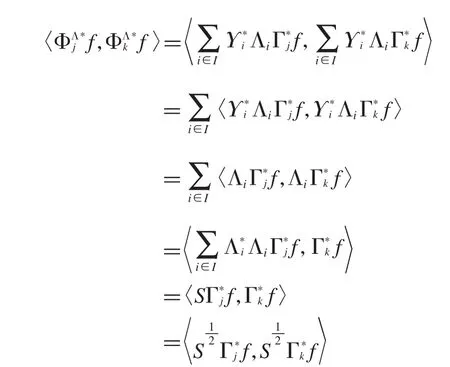
当j＝k时，有故存在酉算子U，使得因为是自伴的，所以可得即酉等价.

性质 2 如果 Λ＝{Λi}i∈I和 Θ＝{Θi}i∈I是 Hilbert空间 H 关于{Hi}i∈I的 g-框架，和分别表示Λ和Θ的第一类g-R-对偶，则下列两个结论等价.

（1）Λ和Θ相似.

证明：因为RT*＝（kerT）⊥，所以由引理1知Λ和Θ相似当且仅当kerTΛ＝kerTΘ，然后根据引理3得证.

性质 3 如果 Λ＝{Λi}i∈I和 Θ＝{Θi}i∈I是 Hilbert空间 H 关于{Hi}i∈I的 g-框架，和分别表示Λ和Θ的第一类g-R-对偶，则下列两个结论等价.

（1）Λ和Θ酉等价.

（2）ΦΛ的 g-框架算子 SΦΛ和 ΦΘ的g-框架算子SΦΘ相同.

证明：Λ和Θ酉等价当且仅当，对∀{gi}i∈I∈kerTΛ，

由引理2，上式等价于

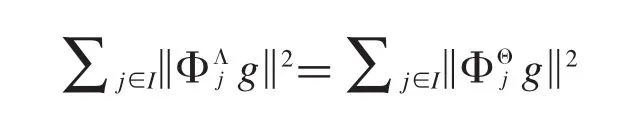
对所有的成立.又因为

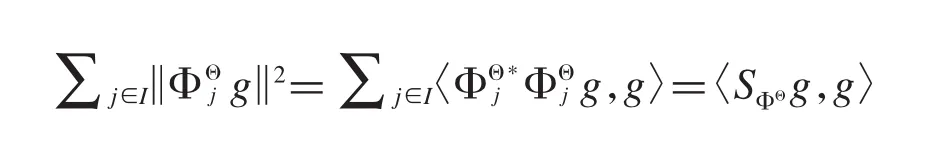
所以可得g-框架算子相同.

性质 4 如果 Λ＝{Λi}i∈I和 Θ＝{Θi}i∈I是 Hilbert空间 H 关于{Hi}i∈I的 g-框架，和分别表示Λ和Θ的第一类g-R-对偶，则下列两个结论等价.

（1）Λ和Θ的g-框架算子相同.

（2）ΦΛ和ΦΘ酉等价.

证明：若是 Λ＝{Λi}i∈I与（Γ，Υ）相关的第一类 g-R-对偶，那么 Λ＝{Λi}i∈I是与（Υ，Γ）相关的第一类 g-R-对偶，见文献[6]的引理 3.3.再由性质 3 可证.

下面将根据第三类g-R-对偶，给出对偶g-框架的一个刻画，为了证明的方便，我们先讨论第一类g-R-对偶和第三类g-R-对偶的一个关系.

定理1设 Λ＝{Λi∈B（H，H）i:i∈I}是H的一个g-框架序列，其g-框架算子为S，Γ＝{Γi∈B（H，H）i:i∈I}和 Υ＝{Υi∈B（H，H）i:i∈I}是g-标准正交基，M:HH是一个满足的有界可逆算子，记为 Λ 与（Γ，Υ，M）相关的第三类g-R-对偶，那么Λ是g-框架当且仅当ΦΛ是g-Riesz序列.

证明：由g-框架的知识得到，是g-Parseval框架，ΥM是g-Riesz基，若其g-Riesz界为见文献[8].假设Λ是一个界为0＜A1＜A2的g-框架，那么对任意有限子集F∈I，有

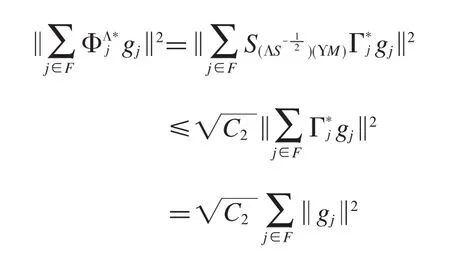
同理可得

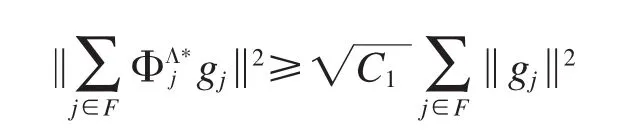
所以ΦΛ是g-Riesz序列.

若ΦΛ是H上的g-Riesz序列，其g-Riesz界为0＜D1＜D2，令g-Riesz基的 g-Riesz 界为 0＜B1＜B2，假设则有一个有限子集F∈I和{gj∈Hj:j∈F}，使得

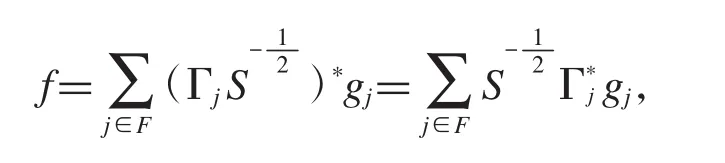
所以有

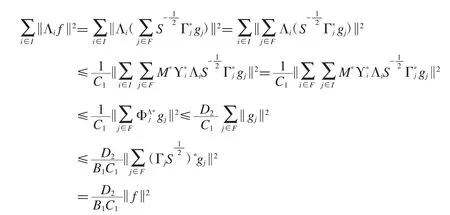
同理可得

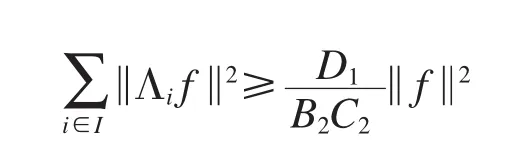
因为所以Λ是H的g-框架.

注3以上的定理给出了g-框架与它的第三类g-R-对偶的一个充要条件，因为任意的g-标准正交基都是g-Riesz基，所以它是文献[6]中定理2.5的一个特例.

定理2设Λ＝{Λi∈B（H，Hi）:i∈I}是H的一个g-框架序列，其g-框架算子为S，是g-Riesz序列，Γ＝{Γi∈B（H，Hi）:i∈I}和Υ＝{Υi∈B（H，Hi）:i∈I}是g-标准正交基，是一个满足的有界可逆算子，那么下面两个结论等价：

（1）Λ 与（Γ，Υ，M）相关的第三类 g-R-对偶是 ΦΛ；

（2）与（Γ，Υ）相关的第一类 g-R-对偶是

证明：（1）⇒（2）由第三类 g-R-对偶的定义有

所以

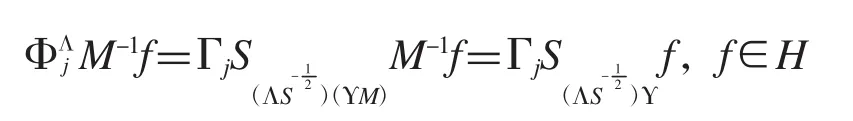
即与（Γ，Υ）相关的第一类 g-R-对偶是{ΦΛjM-1}j∈I.

（2）⇒（1）同理易证.

定理3设 Λ＝{Λi∈B（H，H）i:i∈I}是H的一个g-框架序列，其g-框架算子为S，Γ＝{Γi∈B（H，H）i:i∈I}和 Υ＝{Υi∈B（H，H）i:i∈I}是g-标准正交基，M:HH是一个满足的有界可逆算子，是 Λ 与（Γ，Υ，M）相关的第三类g-R-对偶，那么下面两个结论等价：

（1）Θ是Λ的一个对偶g-框架；

（2）存在一个g-Bessel序列使得对每个gj∈Hj，j∈I，都有

其中表示序列与（Γ，Υ）相关的第一类 g-R-对偶.

证明：首先证明Θ是Λ的一个对偶g-框架是的一个对偶g-框架.若对∀f∈H，有则有

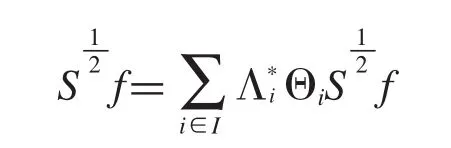
所以有

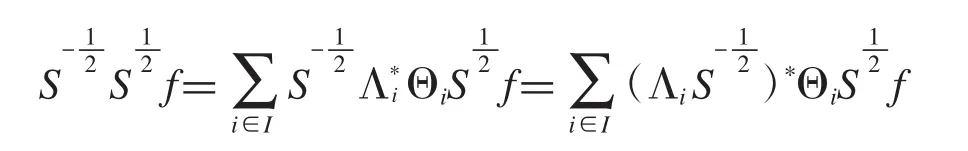
即

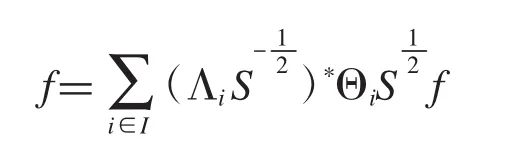
故是的一个对偶g-框架.充分性的证明类似可证.

由定理2可知与（Γ，Υ）相关的第一类 g-R-对偶是因为是g-Parseval框架，所以其g-框架算子是单位算子I，若记序列与（Γ，Υ）相关的第一类 g-R-对偶为则根据引理 4 有，是的一个对偶g-框架⇔（2），所以（1）⇔（2）.得证.

注4定理3是根据第三类g-R-对偶，给出对偶g-框架的一个刻画，它是文献[6]中定理2.9的一个推广，当Λ＝{Λi}i∈I是g-Parseval框架，M＝I时，其中I是单位算子，定理3与文献[6]中定理2.9是一致的.

[1]DUFFIN R J，SCHAEFIEF A C.A class of nonharmonic Fourier series[J].Trans Amer Math Soc，1952，72（2）：341-366.

[2]SUN W C.G-frames and g-Riesz bases[J].Math Anal Appl，2006，322（1）：437-452.

[3]CASAZZA P，KUTYNIOK G，LAMMERS M C.Duality principles in frame theory[J].Fourier Anal Appl，2004，10（4）：383-408.

[4]STOEVA D T，CHRISTENSEN O.On R-duals and the duality principle in Gabor analysis[J].Fourier Anal Appl，2015，21（2）：383-400.

[5]OSGOOEIE，NAJATIA，FAROUGHIMH.G-Riesz dual sequences for g-Bessel sequences[J].Asian-Eur Math，2014，7（3）：383-398.

[6]KHOSRAVI A，TAKHTEH F.Duality principle in g-frames[J].Palestine Journal of Mathematics，2017，6（2）：403-411.

[7]NAJATI A，RAHIMI A.Generalized frames in Hilbert spaces[J].Bull Iranian Math Soc，2011，35（1）：97-109.

[8]KHOSRAVI A，MUSAZADEH K.Fusion frames and g-frames[J].Math Anal Appl，2008，342（2）：1068-1083.

[9]ZHU Y C.Characterization of g-frames and g-Riesz bases in Hilbert spaces[J].Acta Math Sin，2008，24（10）：1727-1736.

[10]XIAO X M，ZHU Y C.Duality principles of frames in Banach spaces[J].Acta Math Sci Ser A Chin，2009，29（29）：94-102.

[11]李登峰，薛明志.Banach空间上的基和框架[M].北京：科学出版社，2007.

[12]CHRISTENSEN O.An introdution to frames and riesz bases[M].Basel：Birkhauser，2016.