DL-8型高压强电离真空计的另一种高灵敏度状态

王竞先，冉书能，荀 坤

(北京大学 物理学院，北京 100871)

电离真空计[1]常被用于测量较高程度的真空(10-8～100Pa)，而经过特殊电极设计的高压强电离真空计[2]则可以在更高的压强下工作，特别适于压强变化范围较大的实验. 其中，DL-8型高压强电离真空计[3-4]具有小阳极-阴极间距与大板状收集极结构，故拥有很低的灵敏度和相应的高压强测量上限(102Pa)[3,5]. 但该种结构不利于低压强测量：一方面，过小的阴极-阳极间距不利于得到长的电子路径；另一方面，2个大的收集极板会接收到大部分由电子高速撞击阳极产生的软X射线，产生较大的光电效应本底电流[4]. 二者结合将会大大限制该电离真空计的压强测量下限.

在特定电极几何结构下，不同电极电势配置会影响电子的路径长度，进而影响灵敏度. 低压强模式下，DL-8型电离规管通过增加1对与阳极电势相同的辅助极和降低阴极电势，使电子可以在更大的区域运动，来增加电子路径和提高灵敏度，成功地使压强测量下限低于10-4Pa[3].

通过数值计算考察了不同电极电势配置下DL-8型电离规管中的电子运行轨迹，发现存在另一种电极电势配置方案，可获得与原配置相当或更高的灵敏度. 此外，还实验考察了相同压强下DL-8型电离真空计读数与电极电势的关系，得到了与数值计算一致的结果.

1 电离规管结构

图1为DL-8型高压强电离规管的结构示意图，图中S代表辅助极，A代表阳极，C代表阴极，B代表板状收集极. 电离规管在工作时由外部电路维持各电极电势，且有稳发射电路保证阴极发射电流恒定. 压强通过收集极电流Ic来测量. 由电离真空计的工作原理，有Ic=sp，其中，灵敏度s近似只与电离规管电极的几何结构和电势配置有关而与压强p无关.

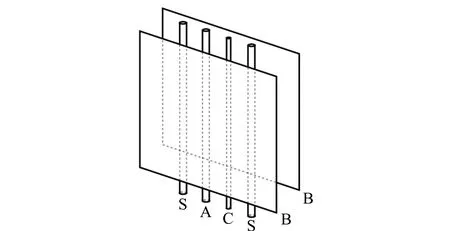
(a) 立体结构

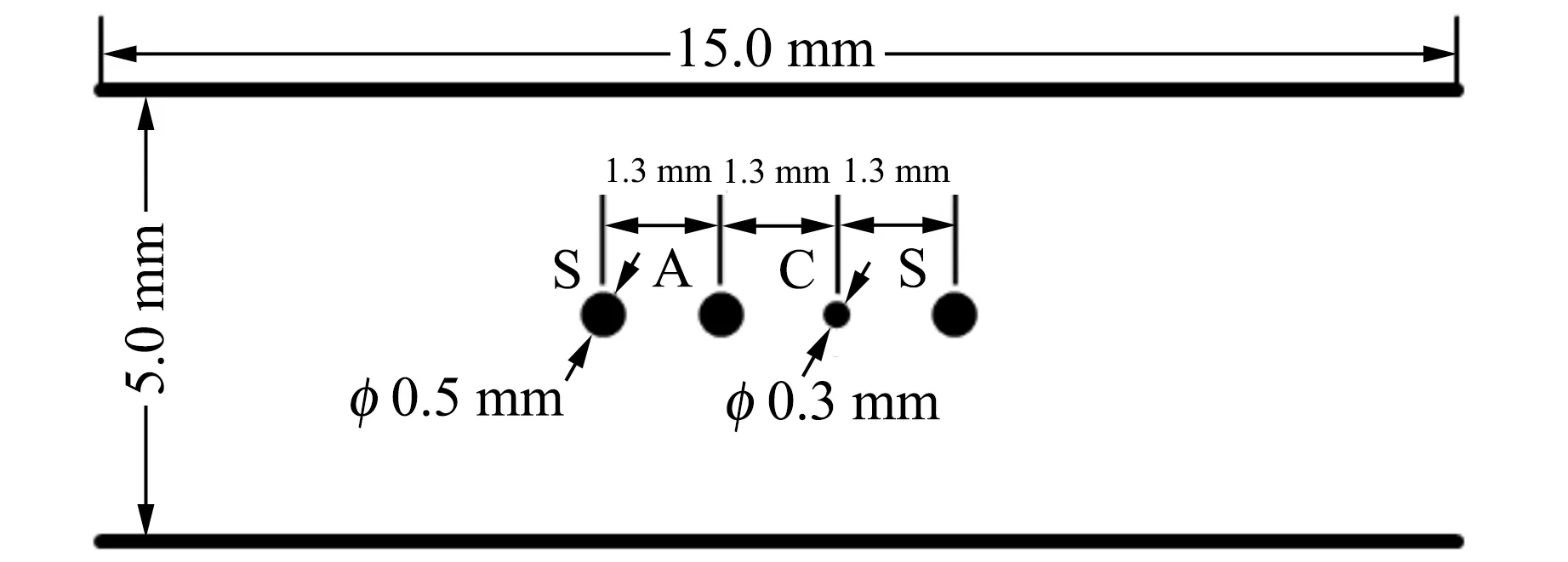
(b) 截面图1 DL-8型高压强电离规管的结构示意图

在低压强测量模式下，DL-8型电离规管的额定工作条件为收集极电势与电源外壳相同(若无特殊说明，各电极电势均是相对收集极而言的)，阴极电势为10V，阳极电势为162V，辅助极电势为162V，阴极发射电流为500μA. 在数值模拟和实验中，维持阳极电势为162V，阴极发射电流为500μA，但将改变阴极和辅助极电势.

2 数值模拟

在数值模拟中，主要讨论电子在电离规管中的运动规律及其与离子碰撞的相对概率.

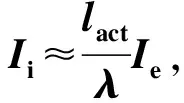
为了简化计算，在进行数值模拟时还作了如下假设：假定电极结构在Z方向有平移对称性，认为电场方向在X-Y平面内，电子在运动过程中无Z方向受力. 由于电子在Z方向速度仅来源于热发射，而热发射电子的能量较低(～0.1 eV)，Z方向速度远小于X-Y平面内的速度，故速度方向也近似在XY方向. 故在后面的讨论中，可近似地认为研究的是二维系统，电场为二维，讨论电子运动时也只讨论X-Y平面内的速度，即只考虑电子的二维运动.

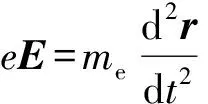
(a)有限元法中采用的网格

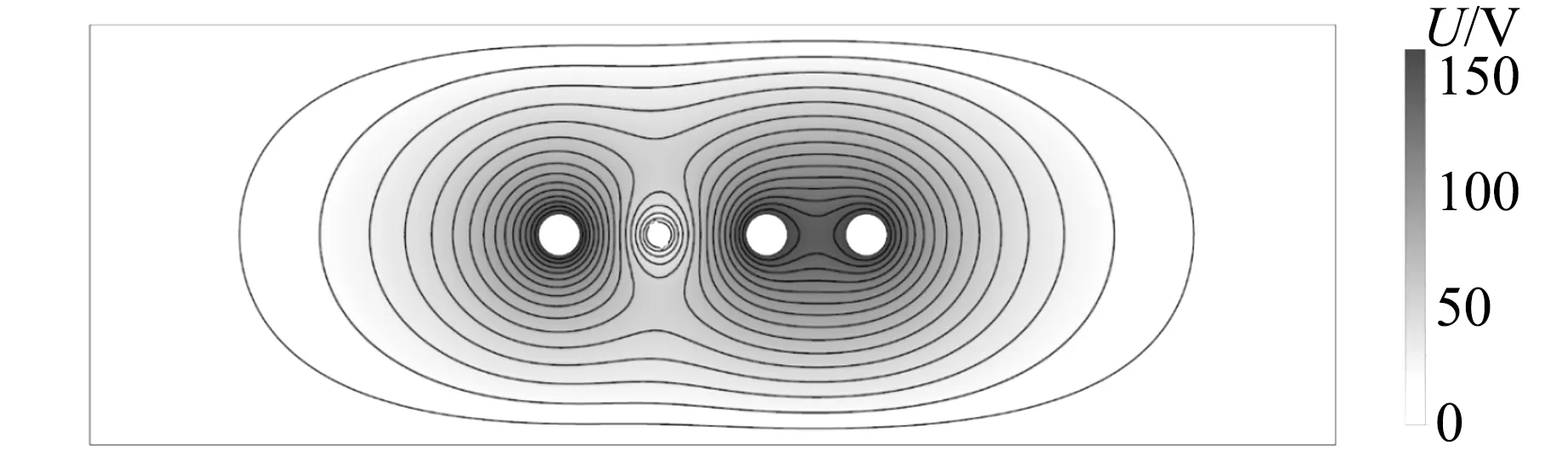
(b)电场解算结果图2 有限元法中采用的网格和电场解算结果

图2(a)为有限元方法计算电场时采用的三角形网格. 可以看出网格足够密且边界上额外加密过，可以保证阳极和阴极表面附近等电场较大处的解也足够精确. 图2(b)为阴极电势10 V、阳极电势及辅助极电势均为162 V时的解算结果. 图中灰度代表电势高低，实线为等势线. 在求解电子在电场中运动时，需求精度取到足够高以至于进一步提高精度，对较长的电子运动轨迹都不会有明显影响.

离子流的大小应该正比于从阴极发出的所有电子的轨迹有效长度之和，但最终会回到阴极的电子不应被计入发射电流. 计入发射电流的电子的平均有效轨迹长度为

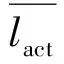
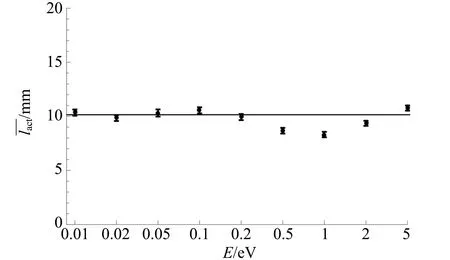
图3 不同发射电子能量下的灵敏度图

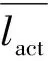
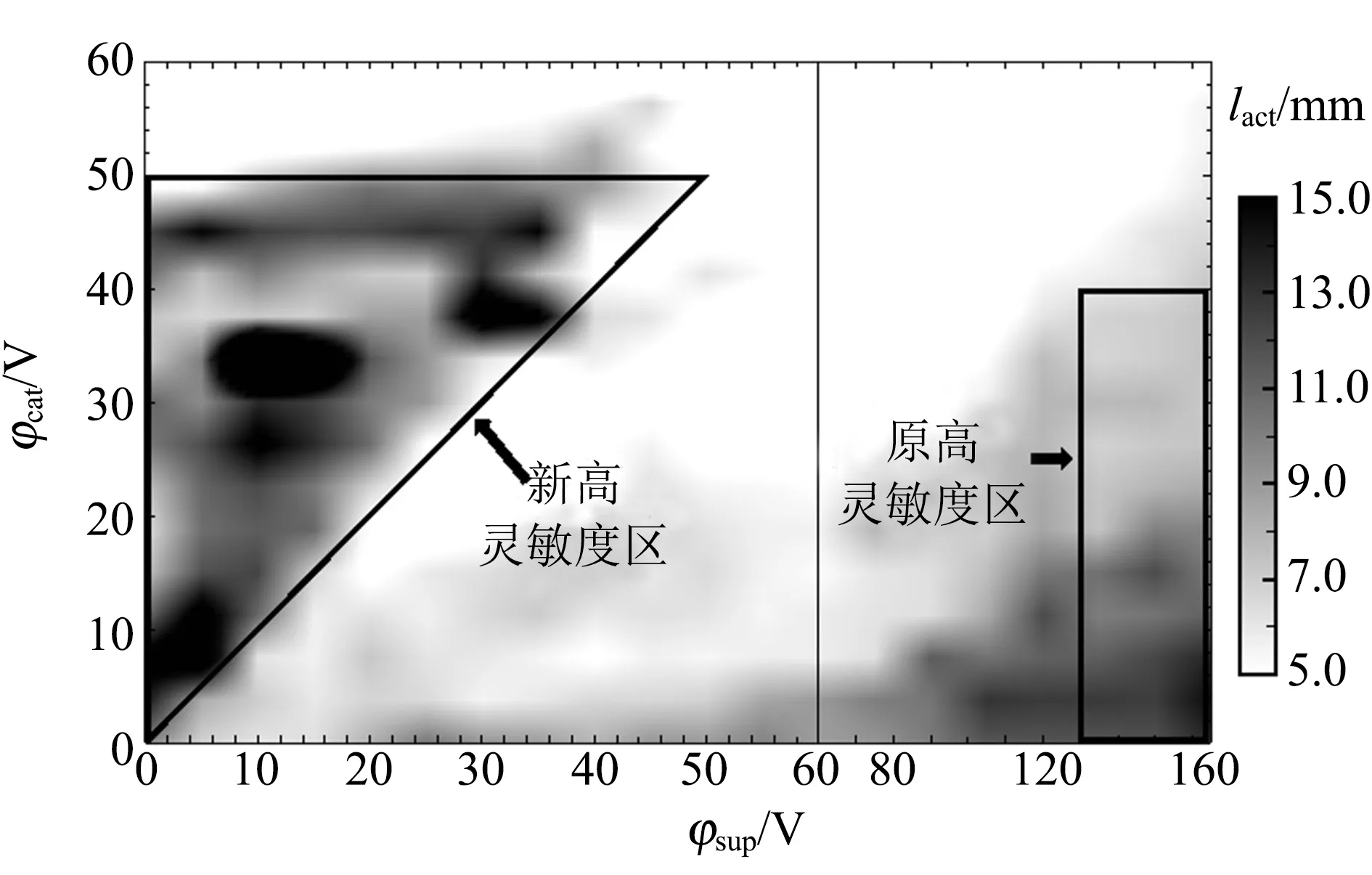
图4 数值模拟结果图

3 理论分析

可以从理论上对新高灵敏度状态作定性解释. 观察电子在不同电极电势配置下的电场中运动的行为可以发现，在新的高灵敏度状态下，电子会倾向于长时间绕阳极旋转. 图5展示了典型的新高灵敏度状态下对应lact较大的电子的轨迹图. 电极电势配置为阴极30 V，阳极162 V，辅助极10 V，发射角度44°，发射能量0.1 eV. 可以看出，电子绕阳极旋转很长时间才到达阳极，走过的路程较长. 图5所示的轨迹通过“数值模拟”节中所述的先求解电场分布再求解电子运动轨迹的方法获得.

图5 电子轨迹图

如图6(a)所示，电子能维持绕阳极转较多圈，得益于在该电势配置下阳极附近区域的电场的对称性较好. 由于电场对阳极近似轴对称，电子相对阳极的角动量接近守恒，衰减会比较缓慢，从而需要较长时间，绕更多圈数才会落到阳极上，灵敏度较高. 而在一些其他的电势配置下，如图6(b)所示，阳极附近电场对称性较差，故电子会快速损失角动量撞上阳极，而且电子还可以到达辅助极，故灵敏度很低. 而在原高灵敏度区，如图6(c)所示，因辅助极电势等同于阳极为162 V,形成了大面积的高电势区域，电子在该区域内运行时受到电场力小且动能较高，可以运行较长路程且在大部分路程中动能大于电离能，因而也可以获得较高的灵敏度.

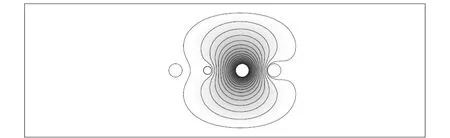
(a)阴极10 V，辅助极5 V

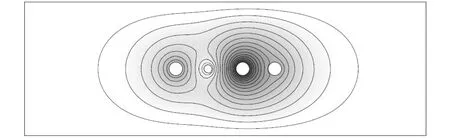
(b)阴极10 V，辅助极80 V

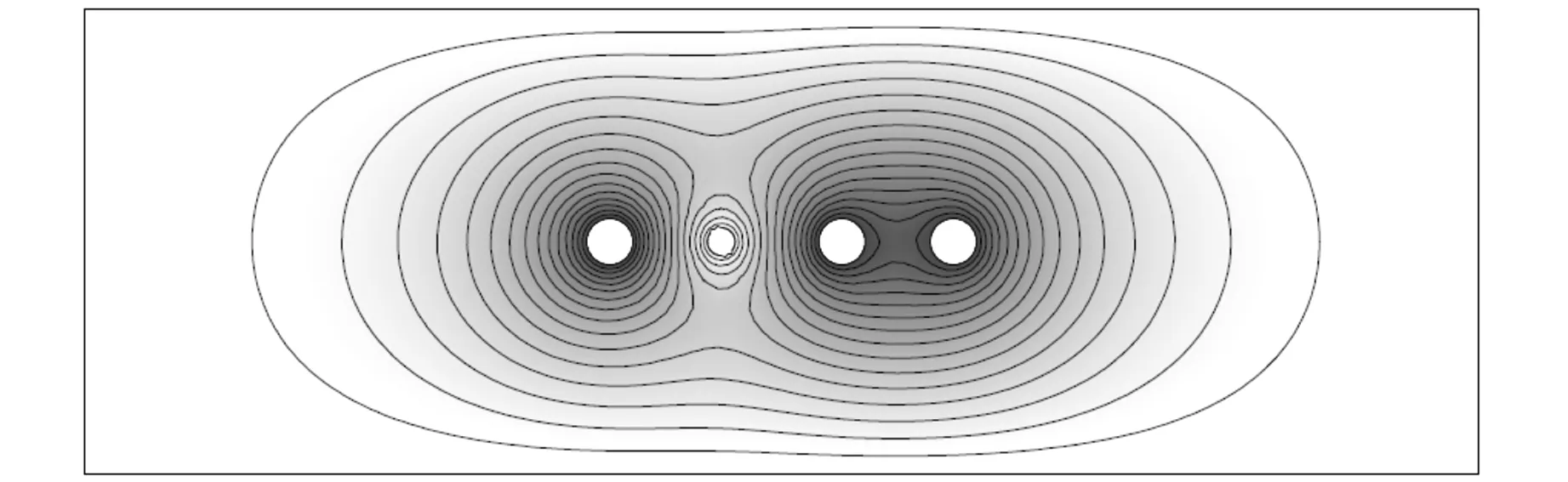
(c)阴极10 V，辅助极162 V图6 不同电极电势配置下的等势线形状图

可以发现，在这2种高灵敏度状态下，获得高灵敏度的机理是完全不同的.

同时，为了使电子被约束在阴极和阳极附近的区域内，要求辅助极电势低于阴极电势，能在左右两侧形成势垒. 且为了使电子在大部分区域内运行时能量较高(大于电离能)，故阴极电势不能过高. 这2条要求限定了高灵敏度区域的范围，结果与数值模拟中给出的范围定性上一致.

4 实验验证

对上述数值模拟和理论分析进行了实验验证. 实验所使用的真空室和DL-8电离规管如图7所示,大真空腔可以保证气压较稳定，右侧接扩散泵-机械泵组合，使真空腔达到高真空状态(10-5Pa量级). 实验中用相同压强下的收集极电流大小来表征相对灵敏度.

图7 真空腔室和DL-8电离规管连接示意图

实验前进行了大于10 h的抽气并对电离规管充分去气[4]，以保证实验过程中电离规管内和真空腔室中的气压近似不变. 实验中始终保持阳极与收集极间电势差为162 V. 使用DL-8型电离真空计电源来保证阴极发射电流恒为500 μA，阴极相对于地的电势为10 V. 采用Keithley2400源表来提供其他电极相对于地的电势.

为进一步保证各次测量和各组测量间电离规管内气压近似一致，对每种阴极电势，分别缓慢增大和减小辅助极电势各测量1次收集极电流取平均，以消除可能存在的气压随时间的缓慢变化. 每次改变阴极电势时，先测量阴极电势为5 V，辅助极电势为0 V时的收集极电流. 只有该值和开始实验时测得的值差别小于20%才可继续实验.

测量结果如图8所示. 图8(a)用点和线表示了不同阴极电势下收集极电流与辅助极电势的关系. 图8(b)用另一种形式来表示了同一实验结果，并标出了2个高灵敏度区域. 可以看出在不同的阴极电势下，流过收集极的电流随辅助极电势上升大致都是先上升，后下降，再上升的趋势，测量区间内两极大值分别在辅助极电势略低于阴极电势和与阳极电势同为162 V时. 这2个极值分别对应数值分析中的新高灵敏度和原高灵敏度区域，且整体规律与数值模拟相符.

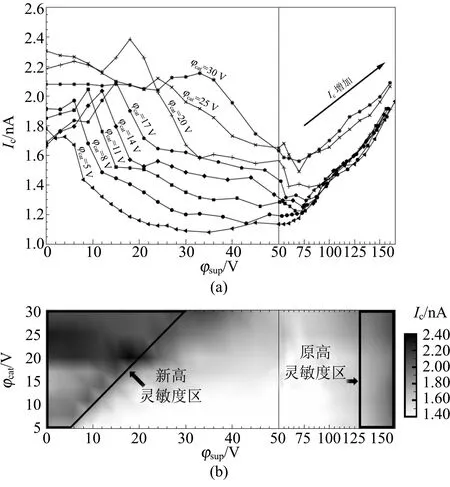
图8 实验结果

5 结 论

数值计算结果表明：DL-8型高压强电离真空计在阴极电势低于50 V且辅助极电势低于阴极电势时，可以达到与原配置(阳极、辅助极电势为162 V，阴极电势为10 V)下相当甚至更高的灵敏度. 此时阳极附近区域的电场有较高对称性,可认为电子是在阳极为心的近似有心力场中运动. 故电子在绕阳极运动时不易损失角动量，从而获得较长的运行轨迹. 实验结果也表明，在一定的阴极电势下，当辅助极电势分别略低于阴极和等于阳极电势时，DL-8型高压强电离真空计的灵敏度都有极值. 数值计算与实验结果基本一致. 这一发现有助于改进DL-8型高压强电离真空计设计并拓宽其测量下限. 在分析过程中使用的数值模拟手段和发现的新机理亦有助于其他电离真空计的设计和优化.

致谢：感谢吴思诚教授对DL-8型高压强电离真空计设计思想的解释和对本文中物理图像和文章撰写提供的宝贵建议.

参考文献：

[1] Bayard R T, Alpert D. Extension of the low pressure range of the ionization gauge [J]. Review of Scientific Instruments, 1950,21(6):571-572.

[2] Schulz G J. Characteristics of the Bayard-Alpert ionization gauge at pressures above 10-5mmHg [J]. Journal of Applied Physics, 1957,28(10):1149-1152.

[3] 郭元恒,吴思诚. 关于电离真空规测量上限非线性的探讨[J]. 物理学报,1979,28(2):250-257.

[4] 西岛忠,郭元恒. DL-8型(日本WIK)高压强电离真空规的一些特性[J]. 真空科学与技术,1986,6(2)79-85.

[5] 宋炳麟，吴思成，郭元恒,等. DL-8型高压强电离规测量氩、氢、氖和氦等气体压强的相对灵敏度[J]. 真空科学与技术,1985,5(1):33-35.

[6] Wolfram Research. 关于内部实现的一些注释 [DB/OL]. http://reference.wolfram.com/language/tutorial/SomeNotesOnInternalImplementation.html#26930.

[7] Wolfram Research. Wolfram 语言中的高等微分方程的数值求解 [DB/OL]. http://reference.wolfram.com/language/tutorial/NDSolveOverview.html.