超声铣削C/C复合材料铣削力的理论建模

高国富，胡二娟，向道辉，赵 波

(河南理工大学 机械与动力工程学院，河南 焦作 454000)

C/C复合材料(碳纤维增强碳复合材料)以碳或石墨纤维为增强体、碳或石墨为基体复合而成，是具有特殊性能的一种新型工程材料。受现阶段加工工艺限制，C/C复合材料存在纤维与基体结合差、孔分布不均匀及制造加工周期长、可还原性差等缺点，使得设计与工程性能受到限制。在纤维结构的特征使其在切削过程中发生纤维脱落、加工面撕裂等问题，所以在铣削C/C复合材料时要考虑到加工材料的结构特点[1]。

铣削钛合金、高温合金和C/C复合材料等难加工材料是航空领域中常用的一种加工方法，铣削力是铣削加工过程的一个重要表征参数。在给定的加工条件下对铣削力的预测已经取得许多成果[2]。Tsai等[3]提出了一种新的端铣刀三维受力模型的几何分析方法，计算了剪切变形区的剪切平面面积和刀具面上的有效摩擦面积，得到了刀具轴向系统的三维切削力。戚厚军等[4-5]采用New-Raphson迭代算法和有限元法，结合铣削路径的曲率变化，对铣削摆线轮廓的铣削力进行了仿真。Yang等[6]利用AdvantEdge有限元软件模拟Inconel 718车削加工过程，分析了切削速度、进给量和切削深度对切削力和温度场的影响。李炳林等[7]基于斜角切削理论对立铣加工过程的铣削力进行预测，提出了斜角切削热力模型。李英松等[8]对铣削力微分模型进行积分得到了总铣削力，应用傅里叶级数变换了多刀齿周期性的总铣削力，简化了铣削力的模型。Karpat等[9]建立了切削力的机械模型，对多向碳纤维增强聚合物复合材料的铣削力的模型进行了研究，获得了铣削加工过程中切削条件对铣削力和表面粗糙度的影响规律。Ojolo等[10]采用机械模型，在刀具工作界面和刀具切屑界面的摩擦模型的基础上，建立铣削力模型。罗智文等[11]基于斜角切削理论对曲线端铣切削力进行建模，得出曲线端铣时铣削力的变化与瞬时进给方向和曲线曲率的关系。Wu等[12]采用正交试验和多元线性回归分析的结果建立了两种铣削力的经验模型。目前，对超声辅助铣削C/C复合材料的铣削力的理论研究较少，且建立的超声铣削力模型，由于考虑铣削加工的铣削深度较小而忽略了螺旋角的影响。螺旋角影响加工时的排屑情况及轴向力的大小，因此，本文在进行铣削力建模时将螺旋角的因素考虑在内。

本文针对超声铣削C/C复合材料进行讨论铣削力模型。首先确定材料的模型及加工方式，即材料碳纤维的方向与铣削时刀具之间的角度关系，然后对铣削进行几何分析。将等效平面和二维正交切削圆结合起来，结合铣刀超声振动辅助的特性，确定了超声铣削时切削刃单元的等效平面角的摆动范围，将铣削模型等效成无数个斜角切削，对铣削力进行分析。本文在对超声铣削C/C复合材料的铣削力进行理论分析时基于立铣刀进行研究，未考虑复合材料的热弹性等材料物理特性。同时，也未考虑实际加工工件的具体形状。

1 C/C复合材料的铣削加工

1.1 C/C复合材料的铣削模型

C/C复合材料属于层状材料，层状材料的纤维方向角(θ)与刀具运动方向的关系直接影响铣削加工时铣削力特征。纤维方向角和铣刀的运动方向间的关系如图1所示。由于复合材料纤维角的存在，铣削过程中，刀具和材料之间的接触随着刀具的旋转而变化。在铣削C/C复合材料的过程中，刀刃的切削方向与材料的纤维方向间的夹角总是在变化着，即纤维切割角(i)是动态变化的[9]，如图1所示。图1为纤维切割角为45°的层状C/C复合材料的碳纤维方向的五个不同的刀具位置的示意图(①，②，③，④，⑤)。

1.2 立铣刀铣削的几何模型

建立立铣刀铣削过程的几何模型，在图2所示的物理模型中构建直角坐标系OXYZ。其中，刀具直径为D，(mm)；刀具的齿数为Z；刀具的转速为n，(r/min)；进给速度为vf，(mm/min)；铣削深度为ap，(mm)；铣削宽度为ae，(mm)。则有：

(1)

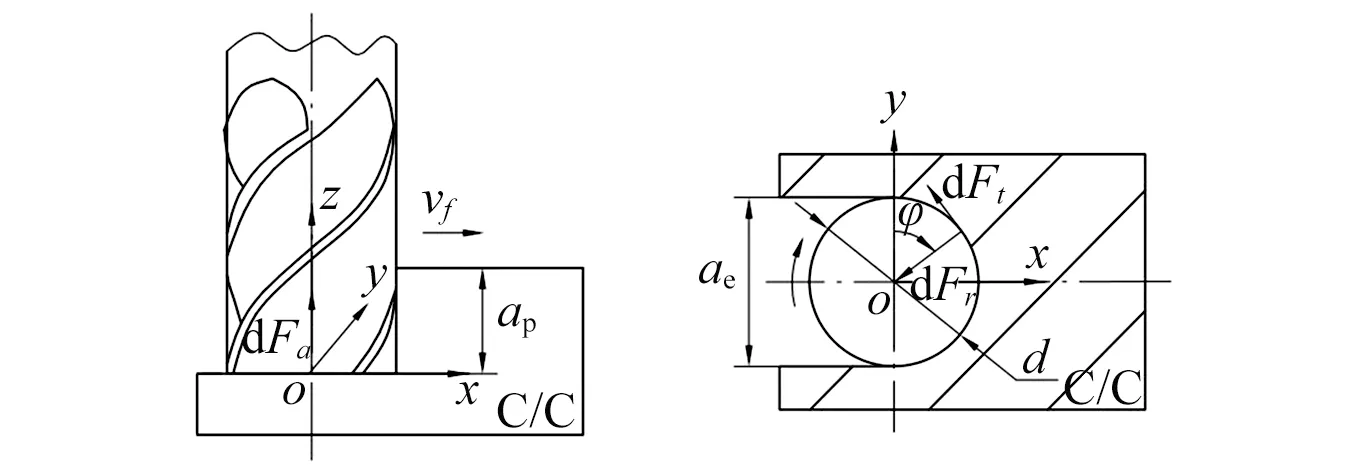
图2 刀具和工件的几何坐标系Fig.2 Geometric coordinates of cutting tools and work pieces

铣削加工过程中，假设刀具径向跳动为零、工件未变形以及刀具未磨损，则每个主切削刃的切削力大小是相同的。铣刀刀刃的螺旋线可以看作是一条在圆柱上的包络线，将铣刀沿圆柱母线展开。考虑到铣刀的切削刃较复杂，将切削刃离散成微斜角切削刃单元。选取其中的一个切削刃微元作为研究对象，取微元的长度为db，则切削刃微元的正交平面和法平面参考系如图3所示。

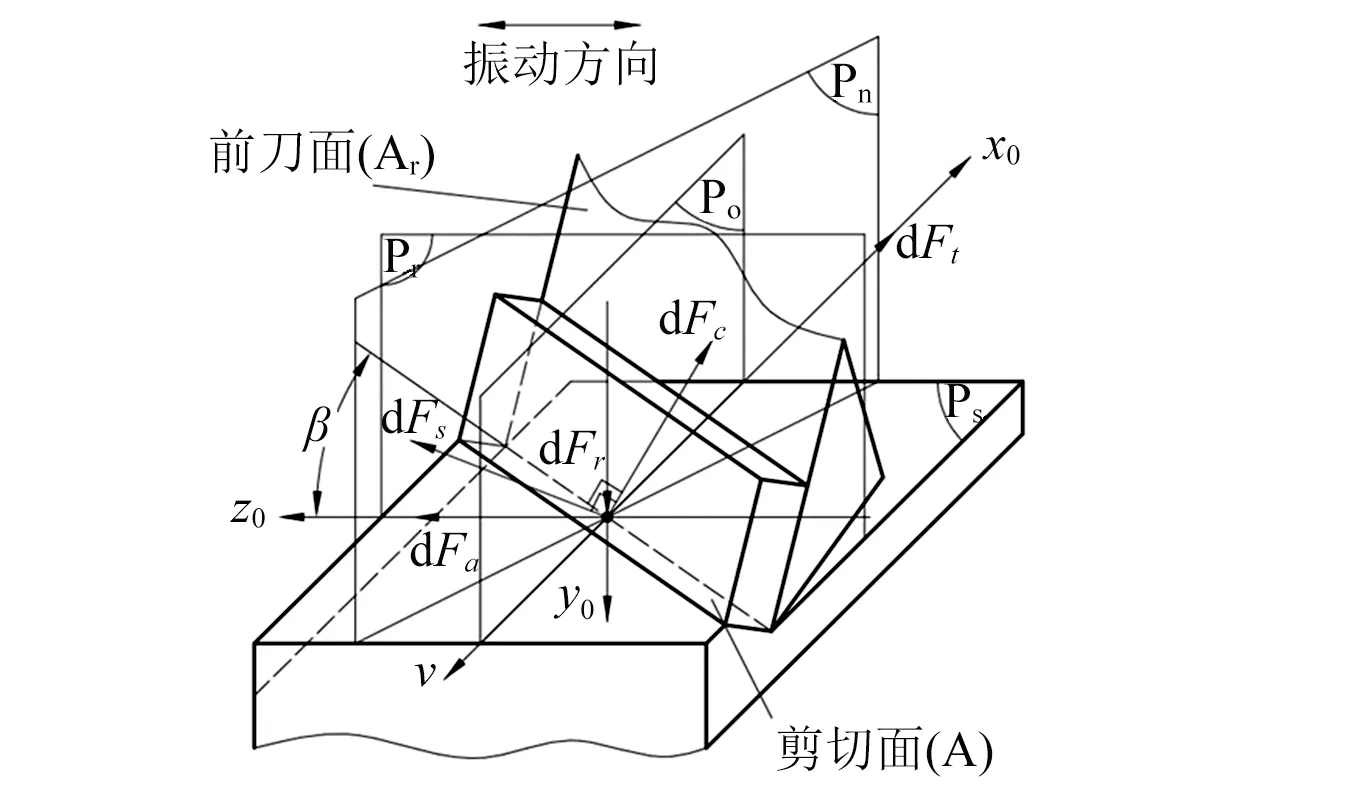
图3 切削刃微元的正交平面及法平面参考系Fig.3 The orthogonal plane and the plane reference frame of micro-element of cutting

由于微元面积较小，可以假设微元斜角切削刃的主剪切面上的剪应力是均匀分布的，则剪切力与剪应力成正比，则铣刀第j个切削刃上的第s个离散处的剪切力为：

dFs=τsdAs

式中：剪切面积dAs=apdb/cosηssinφsn。

切削刃的长度为：

B=LπD/L0cosβ

式中：L是铣刀总刃长；L0是一个导程内参与加工的切削刃长度B0=ap/cosβ。

因此，可以得到：

(2)

根据材料力学平面应力状态理论，主应力方向与最大剪应力方向的夹角应为45°，故在斜角切削的法平面内有：φsn+β′-γn=π/4，因此：

φsn=(π/4)-(β′-γn)

2 超声铣削的铣削力建模

超声铣削C/C复合材料时，沿刀具轴向施加振动，振幅为Z，频率为f的振动，即：

z(t)=Zsin(2πft)

(3)

铣削工件的切削能主要有两部分[3]：剪切能和摩擦能。铣削的总合力R也可以分为两个部分：剪切力Fs和摩擦力Fc。总合力R又分为切向力Ft，径向力Fr和轴向力Fa。

2.1 超声铣削中的斜角切削模型分析

本文采用等效平面法分析铣削力特征，即在切削速度和切屑速度所在的平面内，将斜角切削机理作为二维切削状态的累积，也就是将斜角切削等效为等效平面内的直角切削。则在等效平面内有[7]：

(4)

式中：ηe是等效平面角；ηc是切屑流角；ηs是剪切流角；γn是法平面上的刀具前角；φsn是法平面上的剪切角。

忽略机床等外界条件对铣刀的影响，则当在振动的平衡位置z(t) = 0时，相当于普通铣削时的状态，等效平面角可表示为：ηe=ηe0，ηc=ηc0，ηs=ηs0。在铣刀振动的过程时，切削刃与切屑之间的相互作用是一个变化的值，使得等效平面在超声作用下在一定的范围内摆动，如图4(b)所示，定义摆动角度为j，可知图中B内的摆动范围为2j，当刀刃为达到最大振幅Z处时，因切削刃与切屑之间的相互作用力增大，则使ηc增大，ηs减小；当刀刃为达到最小振幅-Z处时，因切削刃与切屑之间的相互作用力较小，则使ηc减小，ηs增大。因此，在一个振动周期内，某时刻t时，等效平面角ηe，切屑流角ηc，剪切角ηs分别表示为：ηe=ηe0+jt，ηc=ηc0+jct，ηs=ηs0+jst。

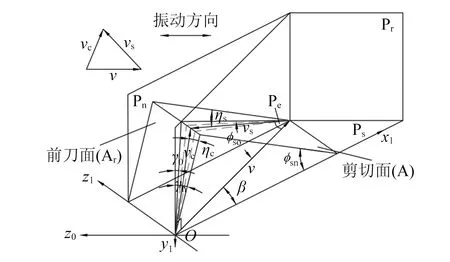
(a)参考平面之间的关系图

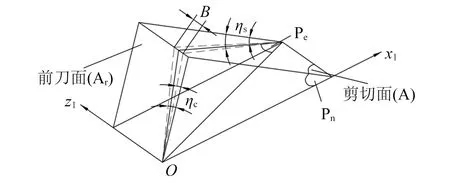
(b)等效平面处的放大图图4 各个参考平面之间的关系Fig.4 The relationship between the reference planes

由Wang的研究结果可知ηc0和ηs0之间的关系为：

(5)

由式(4)和(5)可得：

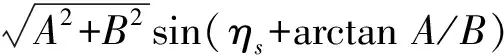
(6)

则式(3)在时刻t时，等效平面的摆动速度vet和剪切速度vs为：

(7)

(8)

由图5、式(7)和(8)及正弦定理可得：

(9)

式中：P=πZcos(φsn-γn)cos 2πft。

在时刻t时，jt可由式子(6)和(9)得：

(10)

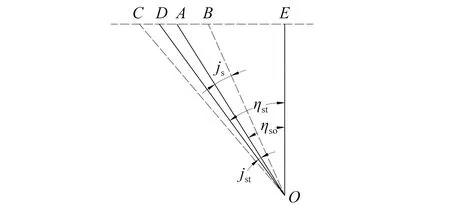
图5 时间为t时剪切面上的剪切流角Fig.5 shear flow angle of shear plane at ts

2.2 超声铣削时铣削力的建模

超声辅助铣削C/C复合材料时，剪切方向角位于等效平面内，剪切力Fs是合力R沿剪切平面的分量，摩擦力Fc是合力R沿切屑平面的分量，即Fs=Rcos(φse+β′-γe) ，Fc=Rsinβ′,得出：

(11)

式中：φse是等效平面内的剪切角；β′是摩擦角，μ=tanβ′；γe是等效平面内的前角。

由图4(a)可知在坐标系(x1，y1，z1)中：

(12)

坐标系(x1，y1，z1)是坐标系(x0，y0，z0)围绕y0轴线旋转了角度β(β< π/2)。在坐标系(x，y，z)中，坐标系(x0，y0，z0)是一个移动的坐标系，以z0轴(刀具轴心)为中心，做圆周运动，运动方向为刀具的旋转方向。则可知在坐标系(x0，y0，z0)中：

(13)

切削刃微元在坐标系(x0，y0，z0)中，Ft是x0方向力的合力，Fr是y0方向力的合力，Fa是z0方向力的合力，可得：

(14)

由式(1)、(13)和(14)可得铣刀切削刃上某一点的切削力：

(15)

其中：a1=cosηscosφsncosβcosφ+

sinηssinβcosφ+cosηssinφsnsinφ

a2=cosηccosγnsinφ-

cosηcsinγncosβcosφ+sinηcsinβcosφ

b1=cosηssinφsncosφ-

sinηssinβsinφ-cosηscosφsncosβsinφ

b2=cosηccosγncosφ+

cosηcsinγncosβsinφ+sinηcsinβsinφ

c1=cosηscosφsnsinβ-sinηscosβ

c2=sinηccosβ-cosηcsinγnsinβ

因铣刀轴向的超声振动，在轴向上的力除了普通铣削加工所受的力外，还有因超声振动所产生的冲击力F。则刀具轴向振动的加速度为：

a=z″(t)-4π2f2Zsin(2πft)

假设刀具等效质量为M，且工件在整个切削过程中受力均匀，则可知工件在轴向受到的冲击力F为：

F=Ma-4π2f2ZMsin(2πft)

(16)

则冲击力F的最小值为0，最大值为4π2f2ZM。

综上可得：

(17)

3 实验研究

C/C复合材料的超声辅助铣削实验(如图6所示)，共分16组进行。实验条件如表1所示，铣削参数的选择如表2所示。对C/C复合材料进行超声铣削加工，一次走刀长度为20 mm。

表1 实验条件Tab.1 Experimental conditions

表2 铣削参数Tab.2 Milling parameter

图6 超声辅助铣削加工实验Fig.6 Ultrasonic assisted milling experiment

选取其中的两组参数进行实验数据统计分析，结果与理论解析的数值模拟预测结果进行对比分析。测量数据的统计分析与相同加工条件下的数值模拟预测对比，如图7和图8所示。从图7和图8可知：x方向的铣削力随着铣刀旋转角度的增加在35°达到最大，在215°达到最小；y方向的铣削力随着铣刀旋转角度的增加在124°达到最小，在305°达到最大；z方向的铣削力随着刀具旋转角度先增后减，在176°达到最大值。不同的铣削参数对C/C复合材料进行铣削所得到的铣削力的波形变化皆以铣刀的旋转角度呈周期性的变化。

实验值产生波动的原因为：x和y方向上主要是C/C复合材料的各向异性所导致，z方向上主要原因有是机床主轴跳动的影响以及C/C复合材料间的结合力，同时加工时产生的切屑也对铣削力的大小产生影响。x方向与y方向的铣削力随铣刀旋转角度的变化规律都是有正弦和余弦曲线构成，铣削力的大小除了跟铣削参数、铣刀的几何尺寸以及超声振动的频率和振幅有关，还与C/C复合材料的碳纤维的方向有关，铣刀切削刃以不同的角度对碳纤维进行切割，实验加工选用的是90°纤维切割角，刀刃切入的方向(x方向)与纤维方向(y方向)垂直。z轴方向的铣削力受到超声振动的影响比x和y方向的大，z轴方向的铣削力，除了超声振动导致剪切流角和切屑流角的摆动变化外，还有超声辅助振动所产生的冲击力。C/C复合材料在制作的过程中，由于挥发损失和碳纤维与碳基体之间的差异收缩形成的孔隙和裂缝，也影响着x，y和z方向的铣削力值的变化。总之，铣削力的影响因素有：工件材料、铣削参数、刀具的几何参数、加工方式和超声振动的参数。

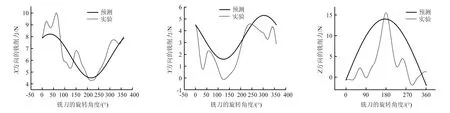
图7 铣削速度：73.48 m/min；每齿进给量：0.05 mm；铣削深度：0.35 mm；铣削宽度：6 mmFig.7 Milling speed：73.48 m/min；Feed per tooth: 0.05 mm; milling depth: 0.35 mm; milling width: 6 mm

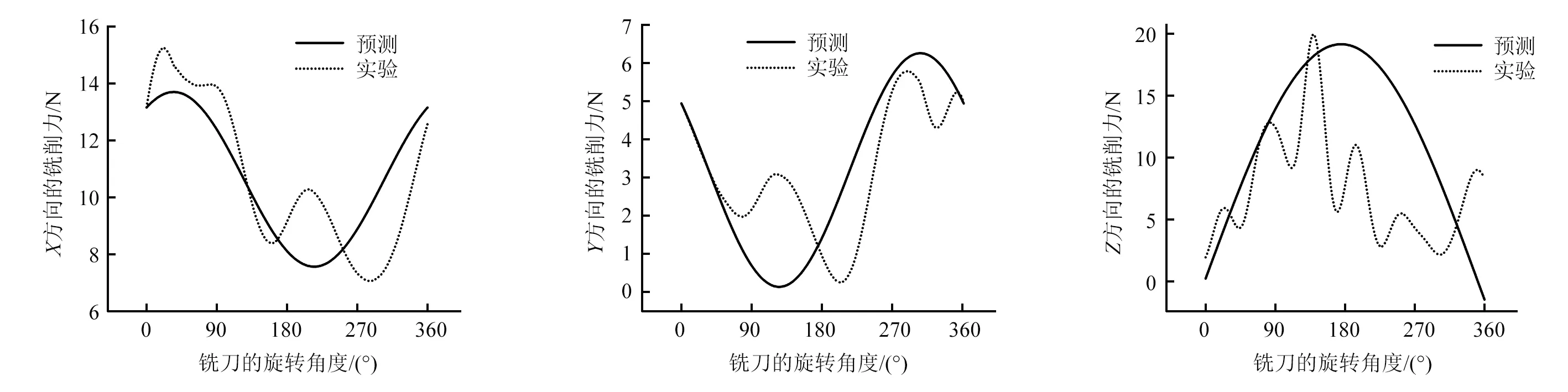
图8 铣削速度：77.24 m/min；每齿进给量：0.05 mm；铣削深度：0.45 mm；铣削宽度：6 mmFig.8 Milling speed：77.24 m/min；Feed per tooth: 0.05 mm; milling depth: 0.45 mm; milling width: 6 mm

4 结 论

本文根据C/C复合材料的层状排布特点，确定了纤维切割角、纤维方向角和刀具瞬时旋转角度之间的关系；根据立铣刀的特点，确定立铣刀的几何模型。基于普通铣削力分析，将铣刀展开，对切削刃微元处理，将微元切削等效为斜角切削，再结合铣削加工中对刀具施加轴向超声的特点，得到了超声铣削中的等效平面角的变化规律，建立了超声铣削C/C复合材料的铣削力模型。结果表明，超声振动对铣削力的三个方向都有影响，该超声铣削方式对所加振动方向的力影响最大，其次是x和y两个方向的力。对C/C复合材料进行超声辅助铣削加工，测得三向铣削力，并对铣削力的模型进行算例计算，结果表明三向铣削力的变化规律和实验测得的规律吻合。

参 考 文 献

[1] SORRENTINO L, TURCHETTA S.Cutting forces in milling of carbon fibre reinforced plastics[J].International Journal of Manufacturing Engineering, 2014(1): 195-196.

[2] WANG S B, GENG L, ZHANG Y F, et al.Cutting force prediction for five-axis ball-end milling considering cutter vibrations and run-out[J].International Journal of Mechanical Sciences, 2015, 96/97: 206-215.

[3] TSAI C L.Analysis and prediction of cutting forces in end milling by means of a geometrical model[J].International Journal of Advanced Manufacturing Technology, 2007, 31(9/10): 888-896.

[4] 戚厚军, 张大卫, 蔡玉俊，等.摆线轮轮廓高速周铣工艺系统的弹性铣削力预测方法[J].机械工程学报, 2009, 45(9): 164-172.

QI Houjun, ZHANG Dawei, CAI Yujun, et al.Modeling methodology of flexible milling force for cycloid on high speed peripheral milling process system[J].Journal of Mechanical Engineering，2009，45(9)：164-172.

[5] QI H, TIAN Y, ZHANG D.Machining forces prediction for peripheral milling of low-rigidity component with curved geometry[J].International Journal of Advanced Manufacturing Technology, 2013, 64(9/10/11/12): 1599-1610.

[6] YANG Z C, ZHANG D H, HUANG X C, et al.The simulation of cutting force and temperature field in turning of inconel 718[J].Key Engineering Materials, 2010, 458: 149-154.

[7] 李炳林, 胡于进, 王学林,等.基于斜角切削理论的立铣切削力预测研究[J].中国机械工程, 2011, 22(19): 2283-2288.

LI Binglin, HU Yujin, WANG Xuelin, et al.Cutting force prediction based on oblique cutting theory in end milling[J].China Mechanical Engineering, 2011, 22(19): 2283-2288．

[8] 李英松, 夏平, 何东璠.基于傅里叶级数的立铣刀铣削力模型[J].机械设计与制造, 2012(7): 256-258.

LI Yingsong, XIA Ping, HE Dongfan.Milling force model for end milling based on the fourier series[J].Machinery Design & Manufacture, 2012(7): 256-258.

[10] OJOLO S J, AGUNSOYE O J, ADESINA O, et al.Force modelling in high speed end-milling of super alloys[J].Journal of Mechanical Engineering & Automation, 2015, 5(1): 56-66.

[11] 罗智文, 赵文祥, 焦黎,等.基于斜角切削的曲线端铣切削力建模[J].机械工程学报, 2016, 52(9): 184-192.

LUO Zhiwen, ZHAO Wenxiang, JIAO Li, et al.Cutting force modeling in end milling of curved geometries based on oblique cutting process[J].Journal of Mechanical Engineering, 2016, 52(9): 184-192.

[12] WU Q Y, HE L, XIAO H, et al.Milling force analysis and modeling of super-alloy GH2132[C].Materials Science Forum, 2016.