灌浆套筒密实度的超声波检测方法

姜绍飞, 蔡婉霞

(福州大学 土木工程学院，福州 350108)

随着社会经济的发展，人们对建筑节能和居住环境等日益关注，装配式建筑的推广成了大势所趋。但是,其连接质量问题仍存在技术不成熟、设备不完善、理论依据不充分等问题，而连接方式中的湿法连接主要采用灌浆套筒连接。灌浆套筒连接利用无收缩灌浆料作为黏结材料连接钢筋以确保荷载传递的连续性[1]。套筒通常采用铸造工艺或机械加工工艺制造[2]，灌浆料以水泥为基本材料，配以细骨料，以及混凝土外加剂和其他材料组成的干混料，加水搅拌，具有良好的流动性、早强、高强、微膨胀等性能[3]。

装配式建筑的套筒灌浆质量属于暗箱，在实际施工中影响梁筋连接套筒灌浆质量的因素不易控制，水平钢筋套筒连接往往存在顶部脱空缺陷，因此施工中如何检测套筒灌浆质量成为工程界普遍关注的问题。近十年来，国内也开始研究灌浆连接技术，但主要是力学性能方面的研究，对其施工或运营阶段的检测或监测却罕见报道。《福建省预制转配式建筑技术规程》[4]和《装配式建筑技术规程》[5]对套筒是否密实的质量检测并没有给出明确方法，而在具体的构件拼装施工中，施工人员很少关注套筒灌浆情况，且没有有效的检测手段，单凭施工人员或监理人员现场监督施工操作并不能判断灌浆是否密实。

国外已有的研究大部分是针对灌浆套筒连接的力学性能，对其施工或运营阶段的检测或监测却极为稀少，仅有的研究尚处于实验室探索阶段。Joel等[6]利用声发射技术来监测单调拉伸下的两种灌浆套筒连接的破坏，以及周期拟静力荷载下使用灌浆套筒连接的预制混凝土桥梁构件的破坏，监测点布置在套筒轴向表面。结果表明：比起钢筋拉断，声发射技术对钢筋拔出更敏感；预制桥梁构件的破坏同其使用的灌浆套筒连接的破坏是同步的。Parks等[7]利用声发射传感器对单向拉伸下两种套筒连接的材料变形和裂纹扩展进行监测，建立声发射信号与损伤的联系。

类似的预应力管道压浆质量检测主要使用超声波法、冲击回波法、电磁法、雷达法和X射线法等。特别是超声波法因其定向性好、穿透性强、无损伤、无污染、能够穿透被检测材料，在机械、航天等领域常用来对材料、焊缝等进行探伤和可靠性评定，近些年广泛用于土木工程材料与结构强度检测评估、内部空洞与裂纹缺陷、表面裂缝检测与定位。Saint-Pierre等[8]运用原位超声波脉冲法对混凝土的损伤程度进行了质量评定，发现该方法即使对损伤程度很低的混凝土仍然很敏感。Ju等[9]则通过测量超声波速、混合波的幅度及衰减，计算声学参数的变化，来评估碱性二氧化硅反应(Alkali-Silica Reaction, ASR)引起的混凝土损伤。这些研究所用的原理都是根据超声波在传播过程中遇到缺陷界面，波的反射、折射、绕射改变了声参数，依据声参数的变化来检测材料与结构的损伤。随着超声波技术的发展和应用，探测混凝土缺陷的超声概率判缺法已写入多部国内外的规范，该方法采用正态分布来近似抽样分布，对采集到的声速进行统计学抽样分布处理[10]。这种做法在样本量较大时(n≥30)，可以采用正态分布来近似抽样分布是合理的，但是当样本量较少(n<30)，用正态分布来近似抽样分布会带来较大的误差，导致检测漏判、误判，引发安全事故。

目前，装配式建筑的梁筋连接套筒灌浆质量还没有有效的检测方法，虽然国内的几本装配式建筑设计规程对装配式建筑的质量验收给出了规定和要求，但是大多是套用现浇式建筑的验收标准，缺少有针对性的技术标准和实际可遵循的质量控制依据。施工中套筒灌浆料是否密实关系到梁筋与梁筋传力是否可靠，进而影响到装配式建筑的整体性能和抗震性能，因此开展灌浆套筒密实度的检测研究具有重要的理论和现实指导意义。

基于此，本文的目的在于研发一种样本量较少时灌浆套筒密实度的检测方法。本文结构如下：首先论证超声波检测灌浆套筒密实度的可行性，即推导超声波首波传播路径，在此基础上，用t分布代替概率判缺法中的正态分布提出了一种新的密实度检测方法用于小样本的抽样检测，最后通过试验验证了所提方法的可行性和有效性。

1 超声波首波在灌浆不密实套筒中的传播

一般来说，利用超声波首波声速判别缺陷的前提条件是：首波通过灌浆料传播的声时必须小于通过套筒壁绕射的声时，否则无法判断套筒内灌浆料灌注质量，因此本文1.2、2.2节对超声波首波路径进行论证。

1.1 灌浆不密实首波路径

超声波在灌浆套筒中传播遇到脱空缺陷时，由于脱空缺陷一般充填空气或水汽，套筒壁与空气或水汽的特性阻抗相差悬殊，导致超声波难以透过缺陷。低频超声波由于漫射而绕过脱空缺陷传播，此时传播路径变长，声时变大。

(1)绕射脱空区后透射灌浆料

有脱空时,首波可能沿路径1传播, 如图1(a)所示，即首波沿套筒壁绕射再透射灌浆料到达接收探头[11]。首波声时计算如下：

(1)

式中：T1为首波沿路径1传播声时，μs；t为套筒壁厚，mm；vs为超声波在套筒中传播速度，km/s；vc为超声波在灌浆料中传播速度，km/s；LAC为套筒壁AC弧长，mm；LCB为透射距离CB长度，mm。

图1 灌浆不密实水平接头首波可能路径Fig.1 The possible path of first-arriving wave for not fully grouted horizontal connectors

(2)透射脱空区后透射灌浆料

有脱空时,首波可能沿路径2传播, 如图1(b)所示，即沿直径方向透射脱空区再透射灌浆料[12]。首波声时计算如下：

(2)

式中：T2为首波沿路径2传播声时,μs；D为套筒外径,mm；d为钢筋直径,mm；va为超声波在空气中传播速度,km/s；x为脱空厚度,mm；t、vs、vc为与式(1)相同。

(3)沿套筒壁环向传播

有脱空时，如图1(c)所示首波可能沿路径3传播，即沿套筒壁环向传播到达接收探头[11]。此时,首波声时计算如下：

(3)

式中：T3为首波沿路径3传播声时,μs；t、vs、D为与式(2)相同。

1.2 脱空情况首波路径论证

根据《装配整体式混凝土结构技术规程(暂行)》[13]：“套管灌浆连接钢筋直径不宜大于30 mm；……机械连接不宜小于16 mm”。结合工程实际，预制住宅、商业建筑灌浆套筒连接技术常用于连接直径为18、20、22、25 mm的梁筋。下面对表1所示上海住总工程材料有限公司的4种型号套筒进行灌浆不密实首波路径的论证。

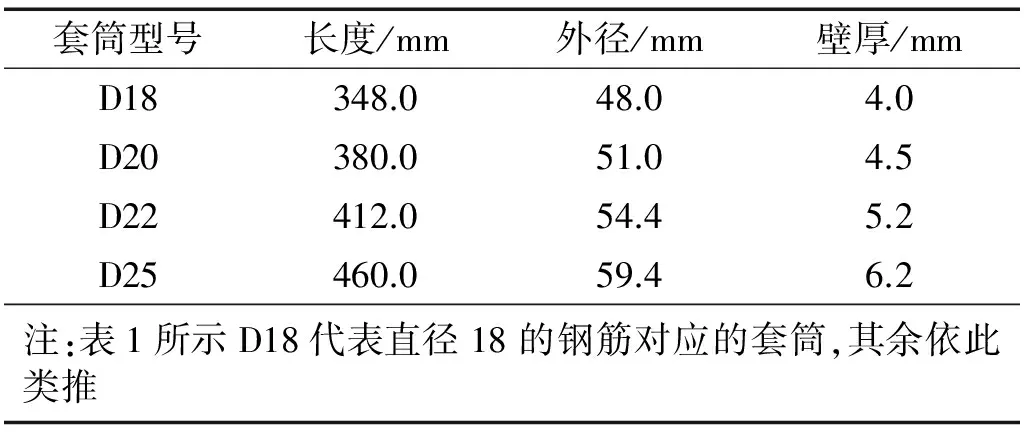
表1 4种型号套筒的尺寸参数Tab.1 Dimension of 4 kinds of sleeves

式(4)括号内为D20、D22、D25替换原不等式对应项的表达式。

T2>T3，将t=4 mm、D=48 mm、d=18 mm代入式(2)和(3)，要满足T2>T3，必须满足：

(4)

超声波首波在钢筋和套筒中传播的速度是vg≈vs≈5 500 m/s[14]，在灌浆料中传播的速度vc≈4 900 m/s[11]，在空气中传播速度va≈340 m/s。

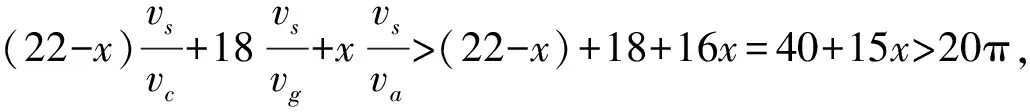
40(42、44、47)+15x>20π(21π、22π、23.5π)

(5)

当x>1.522 mm(1.598、1.808、1.988)，式(5)恒成立。x<1.522 mm(1.598、1.808、1.988)，灌浆套筒体积密实度为98.5%以上，考虑到灌浆料强度发展过程中膨胀剂会膨胀而填满这种非常小的脱空，因此这种情况等同于灌浆密实。

T3>T1，要满足这种情况，必须满足：

(6)

(7)

考虑的最不利工况是套筒灌浆只有50%密实，由图1(a)可见0<α<π/4，由vs≈5 500 m/s和vc≈4 900 m/s得vs/vc≈1.1，其中α是BA和BC间夹角，因此，

即式(7)恒成立。

因此，根据首波沿声时最小路径传播，T2>T3>T1，脱空情况首波路径为绕射脱空区后透射灌浆料。

2 超声波首波在灌浆密实套筒中的传播

2.1 灌浆密实首波路径

套筒灌浆密实，首波沿路径4径向(直径方向)传播[15]，如图2所示，传播路径为连接发射探头和接收探头的直线。此时，首波声时计算如下：

(8)

式中：T4为首波沿路径4传播声时(μs)；D、t、vs、vg、vc、d与1.1节相同。

图2 灌浆密实首波路径(路径4)Fig.2 Path of first-arriving wave for fully grouted sleeves (Path 4)

2.2 灌浆密实首波路径的论证

本节灌浆密实首播路径的论证适用的套筒型号同表1，括号内为D20、D22、D25替换原不等式对应项的表达式。

vg≈vs≈5 500 m/s，vc≈ 4 900 m/s，根据t=s/v，明显图3所示沿径向直线传播的路径声时最小。

图3 灌浆密实首波可能路径Fig.3 Possible path of first-arriving wave fully grouted sleeves (Path 4)

考虑到灌浆密实考虑首波也可能绕射套筒壁传播，下面对T3>T4首波声时进行论证。

将t=4 mm、D=48 mm、d=18 mm代入式(3)和(8)，要满足T3>T4，必须满足：

(9)

vs/vc>1，代入式(9)得：vs/vg<2.268(2.199、2.142、2.073) 恒成立。

因此，根据首波沿声时最小路径传播，灌浆密实首波沿径向直线传播。

2.3 脱空情况声时与密实情况声时比较

T1>T4时，将t=4 mm、D=48 mm、d=18 mm、vs/vg≈1代入(1)和(8)，要满足T1>T4，必须满足：

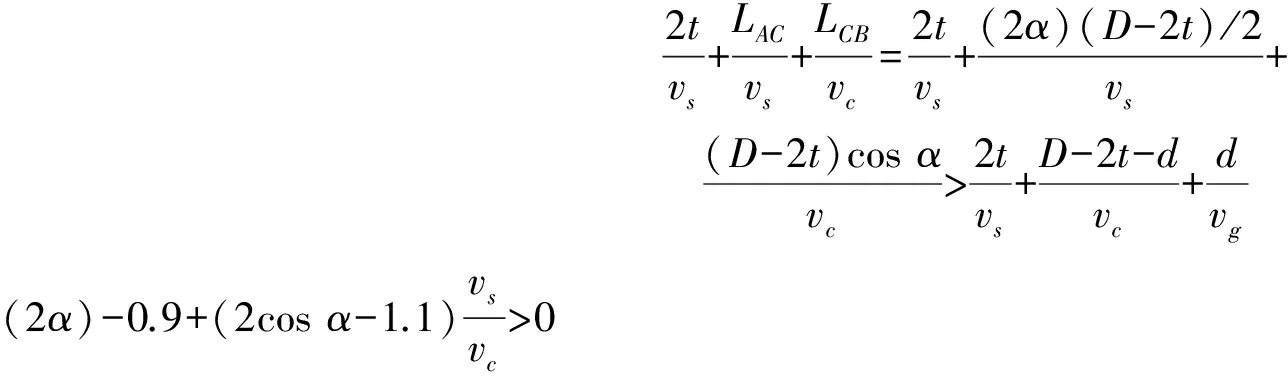
同理，

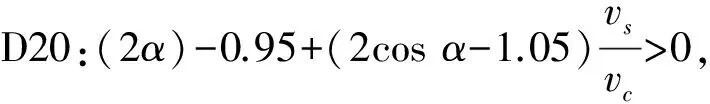
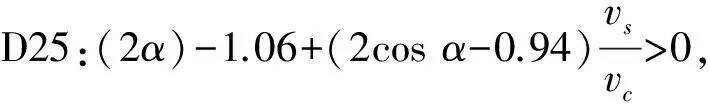
通过1.2、2.2、2.3节分析得出如下结论：在套筒灌浆料及工艺的影响下，灌浆密实时首波沿径向直线传播，有脱空时首波绕射脱空区后透射灌浆料，且有脱空缺陷的声时均大于灌浆密实声时。以发射、接收探头间的距离作为传播距离，传播距离固定的情况下，根据t=s/v，声时增大，声速就减小。超声概率判缺法就是通过统计声速来求出灌浆密实与否的判断值。

3 基于t分布的超声概率判缺法

3.1 超声概率判缺法运用于灌浆套筒密实度检测的可行性分析

概率判缺法[16]指出混凝土的质量波动符合正态分布，因此测得的声学参数也符合正态分布，生产过程中的漏振、漏浆等造成的缺陷的分布不符合正态分布。对灌浆套筒，由于尺寸小，测量声速时，随机误差包括套筒尺寸并非绝对圆形、套筒壁厚并非绝对均匀、钢筋凸肋及灌浆料强度的影响，造成的声速值波动都不可忽略，粗略认为这些随机误差叠加后还是随机误差[17]，同时认为观测数据的随机误差一般服从正态分布。在实际工程中，抽取足够多的样本容量进行调查意味着人力、物力、财力和时间的增加，因此有必要研究小样本的抽样检测问题。根据统计学抽样分布原理，若样本量较大时(n≥30)，可以采用正态分布来近似抽样分布；但是若样本量较少(n<30)，用正态分布来近似抽样分布可能会带来较大的误差，此时可以利用t分布来近似，即用t分布代替概率判缺法中的正态分布来统计求出声速判断值。

3.2 基于t分布的概率判缺法检测步骤

mx=∑Xi/n

(10)

(11)

X0=mx-λ·sx

(12)

X0=mx-t·sx

(13)

式中：λ和t为在统计对象个数n和置信度β一定的情况下查统计学书中的标准正太分布表和t分布表得到的值。常取β的一些标准值有0.01、0.05、0.10等，本文β均取0.02。

(1)在施工工艺与施工条件不变的情况下，采集声速数据。

(2)将各测点的声速由大到小按顺序排列，即X1≥X2≥…≥Xn≥Xn+1……，将排在后面明显小的数据视为可疑，再将这些可疑数据中最大的一个(假定Xn)连同其前面的数据按式(10)、式(11)计算出mx及sx，并按式(13)计算出异常情况的判断值(X0)，其中式(13)是替换原概率判缺法的式(12)。

(3)将判断值(X0)与可疑数据的最大值(Xn)比较，当Xn不大于X0时，则Xn及排列于其后的各数据均为异常值，并且去掉Xn，再用X1-Xn-1进行计算和判别，直至判不出异常值为止；当Xn大于X0时，应再将Xn+1放进去重新计算和判别。

(4)统计算出判断值后，在施工工艺与施工条件不变的情况下，可将其作为判断其他套筒灌浆密实与否的标准。

4 试验研究

4.1 试验概况

本试验所用套筒和灌浆料生产单位为上海住总工程材料有限公司，注册商标为优耐特，钢筋为HRB400钢筋，试验中使用的D18套筒的相关参数见表1。人工灌注灌浆密实的套筒51个，不同程度脱空的套筒9个。其中灌浆密实度控制方法如下：套筒两头均有橡胶塞，将橡胶塞剪去相应脱空面积，灌浆时当浆体灌到设置的橡胶塞高度，多余的浆体就从橡胶塞缺口处流出，达到控制密实度的目的。

灌浆料是以水泥为基本材料，配以细骨料，以及混凝土外加剂和其他材料组成的干混料。钢筋套筒灌浆连接的原理：钢筋从中空型套筒的两端开口穿入其内部，将灌浆料从灌浆口注入，即完成钢筋续接动作，其中注浆可以采用人工注浆或者机械注浆。灌浆料中添加的膨胀剂对其硬化过程中体积变化的影响较小，主要起到填充孔隙的作用，所以通过控制灌浆料体积对灌浆连接套筒密实度进行分级是可行的。由于超声波声速随灌浆料强度发展而提高[18]，灌浆套筒均养护28天。

4.2 检测过程与结果

采用沿套筒横截面径向(直径方向)对测法采集声速，表2序号1-51为灌浆密实声速值，序号52-54为90%体积密实声速值，序号55-57为70%体积密实声速值，序号58-60为50%体积密实声速值。

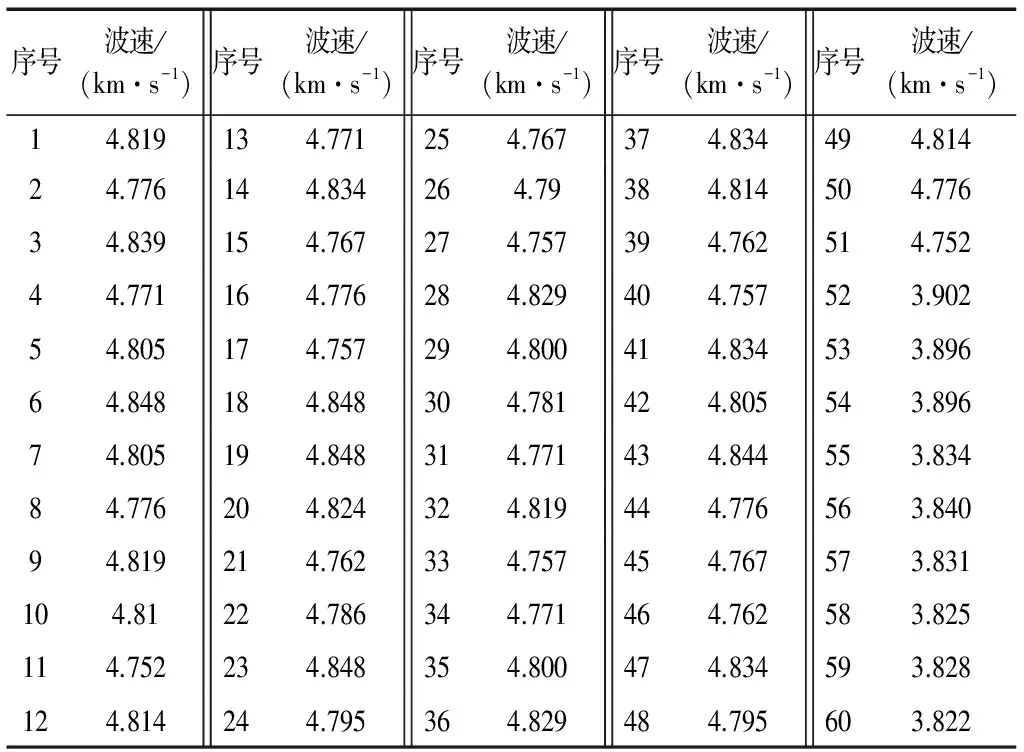
表2 声速表Tab.2 Table of sound velocity

图4 声速值散点图Fig.4 Scatterplot of sound velocity

4.2.1 基于正态分布的概率判缺法

4.2.1.1 工况一(n=51)

为便于理解，首先用灌浆密实声速(序号1-51)统计计算出判断值，灌浆不密实声速(序号52-60)用来验证判断值的正确性。

表3 统计的声速个数n与对应的λ值Tab.3 The number of sound velocity n and the corresponding λ

(1)根据式(10)和式(11)求序号1-51声速平均值mx=4.797 km/s、标准差sx=0.031；

(2)查表3得n=51时分位值λ=2.06，根据式(12)算得异常情况判断值X0=4.733 km/s；

(3)灌浆不密实的9个套筒测得声速与判断值比较，均小于4.733 km/s，判定这9个套筒顶部有脱空缺陷。

4.2.1.2 工况二(n=60)

工况一中参与统计的序号1-51声速值中没有包括脱空声速值(序号52-60)，实际应用中预先并不知道哪些测值是异常值，所以工况二用混杂了灌浆不密实声速的60个测值(表2所示)来统计计算判断值，此时根据3.2节中的(2)，(3)首先对明显的可疑值予以剔除，得到一试算的判断值。然后进行判断、取舍并反复计算，最后才能得到正式的判断值。

(1)表2数据重新排列后如表4，序号52-60声速值明显可疑，根据式(10)，(11)算出序号1-52声速平均值mx=4.780 km/s、标准差sx=0.128；查表3得分位值λ=2.07，根据式(12)算得X0=4.515 km/s；

(2)序号1-52声速值可疑数据最大值3.902 km/s小于X0，则序号52-60声速值为异常值；

(3)计算序号1-51声速平均mx=4.797 km/s、标准差sx=0.031；查表3得分位值λ=2.06，根据式(12)算得异常情况判断值X0=4.733 km/s；序号1-51声速值均大于X0，判不出异常值，停止计算，则此时X0为最终声速判断值。

表4 重新排列后声速表Tab.4 Table of rearranged sound velocity

4.2.2 基于t分布的概率判缺法(n=20)

为研究小样本抽样检测问题，验证本文所提出的方法，从人工灌注的51个密实套筒和9个脱空套筒中采集20个声速值，序号1-17为灌浆密实声速值，序号18-20为脱空声速值，用混杂了灌浆不密实声速的20个测值(表5所示)来统计计算判断值。

表5 声速表Tab.5 Table of sound velocity

(1)表5数据重新排列后如表6，序号18-20声速值明显可疑，根据式(10)、式(11)算出序号1-18声速平均值mx=4.740 km/s、标准差sx= 0.212；查表7得分位值t=2.26，根据式(13)算得X0=4.281 km/s；

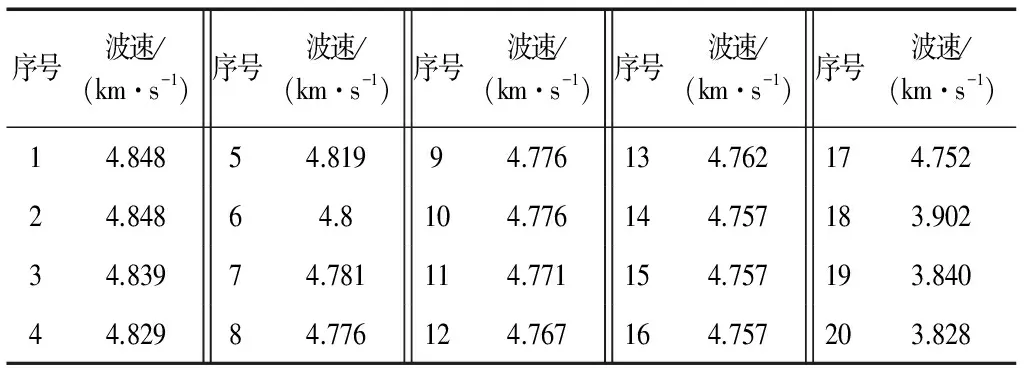
表6 重新排列后声速表Tab.6 Table of rearranged sound velocity

(2)序号18-20声速值可疑数据最大值3.902 km/s小于X0，则序号18-20声速值为异常值；

(3)计算序号1-17声速平均值mx=44.796 km/s、标准差sx=0.030；查表7得t=2.27，根据式(13)算得X0=4.728 km/s；序号1-17声速值均大于X0，判不出异常值，停止计算，则此时X0为最终声速判断值。

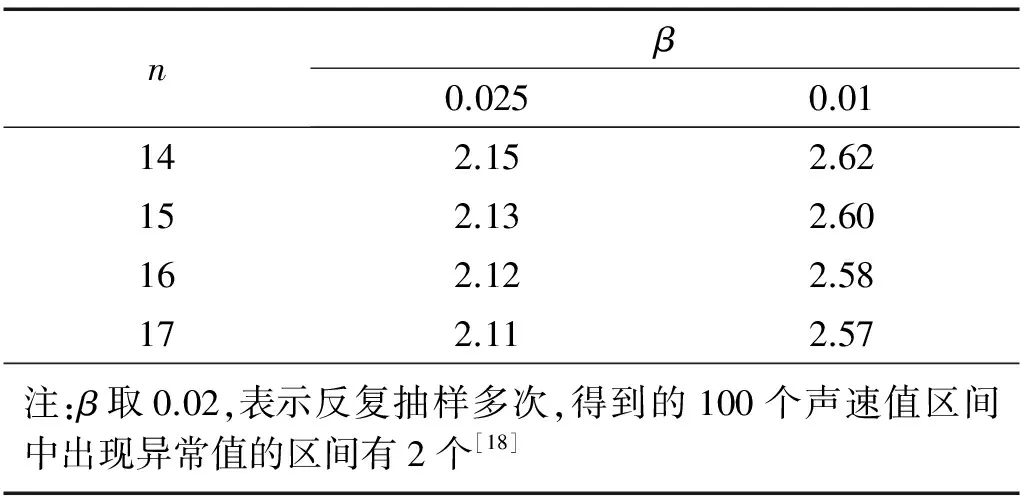
表7 统计的声速个数n与对应的t分布上分位值Tab.7 The number of sound velocity n and the corresponding upper fractile for t-distribution

4.3 比较与讨论

改进前后的超声概率判缺法对比如表8，可见样本容量前者比后者多2倍的情况下，统计算得判断值极为接近，前者为完全密实理论声速的0.970倍，后者为0.969倍，因此改进后的概率判缺法在减少抽样工作量的同时又不会降低缺陷判别效果，提高了检测效率。

表8 对比表Tab.8 Table of comparison

5 结 论

(1)本文对超声波首波在灌浆套筒中的传播路径进行分析和理论推导，结果表明灌浆密实时首波沿径向直线传播，有脱空时首波绕射脱空区后透射灌浆料，且有脱空缺陷的声时均大于灌浆密实声时，证明利用超声波首波声速判别套筒灌浆脱空缺陷的前提条件是成立的。

(2)提出了基于t分布的超声概率判缺法，可以用于小样本抽样的灌浆套筒密实度检测，试验表明提出的检测方法在减少抽样工作量的同时又不会降低缺陷判别效果，提高了检测效率。

参 考 文 献

[1] LUTX L A, GERGELY P.Mechanics of bond and slip of deformed bars in concrete[J].American Concrete Institute Journal, 1967,64(11): 100-108.

[2] 中华人民共和国住房和城乡建设部.JG/T 398—2012钢筋连接用灌浆套筒[S].北京: 中国标准出版, 2012.

[3] 中华人民共和国住房和城乡建设部.JG/T 408—2013钢筋套筒连接用灌浆料[S].北京: 中国标准出版, 2013.

[4] 福建省住房和城乡建设厅.DBJ 13-216—2015福建省预制转配式建筑技术规程[S].福州: 福建科学技术出版社.2015.

[5] 中华人民共和国住房和城乡建设部.JGJ 1—2014转配式建筑技术规程[S].北京: 中国建筑工业出版社, 2014.

[6] PARKS J E, PAPULAK T, PANTELIDES C P.Acoustic emission monitoring of grouted splice sleeve connectors and reinforced precast concrete bridge assemblies[J].Construction and Building Materials, 2016,122: 537-547.

[7] JOEL EDGAR P.Seismic rehabilitation of column to pier cap accelerated bridge construction connections and acoustic emission monitoring assessment[D].University of Utah, US, 2014.

[8] SAINT-PIERRE F, PHILIBERT A, GIROUX B, et al.Concrete quality designation based on ultrasonic pulse velocity[J].Construction and Building Materials, 2016, 125: 1022-1027.

[9] JU T, ACHENBACH J D, JACOBS L J, et al.Ultrasonic nondestructive evaluation of alkali-silica reaction damage in concrete prism samples[J].Materials and Structures, 2017, 50(1): 60.

[10] 徐国祥.统计学[M].上海: 上海人民出版社, 2007: 180-181.

[11] 刘永前, 张彦兵, 邹振祝.超声波检测钢管混凝土拱桥密实度的试验研究[J].北方交通大学学报, 2004, 28(4): 54-57.

LIU Yongqian, ZHANG Yanbing, ZOU Zhenzhu.Study on ultrasonic detection and evaluation for the deficiency of concrete-filled steel tube arch bridge[J].Journal of Beijing Jiaotong University, 2004, 28(4): 54-57.

[12] 潘卫育, 赵讳, 李传勇, 等.超声波检测钢管混凝土密实度[J].中国铁道科学, 2005, 26(3): 64-67.

PAN Weiyu, ZHAO Hui, LI Chuanyong, et al.detection on the density of steel tube concrete by ultrasonic wave[J].China Railway Science, 2005, 26 (3): 64-67.

[13] 辽宁省住房和城乡建设厅.DB21/T1868—2010装配整体式混凝土结构技术规程(暂行)[S].2010.

[14] 杨凤民.铸铁件的超声波检测[J].现代铸铁, 2001(4): 61-64.

YANG Fengmin.Ultrasonic flaw-detection of iron castings[J].Modern Cast Iron, 2001 (4): 61-64.

[15] 张宏, 余钱华, 吕毅刚.超声透射法检测钢管拱桥拱助混凝土质量应用研究[J].土木工程学报, 2004, 37(8): 50-54.

ZHANG Hong, YU Qianhua, LÜ Yigang.Application study of quality testing of the arch-rib concrete of concrete-filled steel tube arch bridge by ultrasonic transmission method[J].China Civil Engineering Journal, 2004, 37 (8): 50-54.

[16] 王五平, 宋人心, 傅翔.超声探测混凝土缺陷的概率判断法辨析[J].混凝土, 2011(2): 7-9.

WANG Wuping, SONG Renxin, FU Xiang.Critical analysis of probability method on ultrasonic detection of defects in concrete[J].Concrete, 2011(2): 7-9.

[17] 姚应生, 董烈镛.测量误差检验与数据处理[M].北京: 煤炭工业出版社, 1991: 1-14.

[18] 吴小宝, 林峰, 王涛.龄期和钢筋种类对钢筋套筒灌浆连接受力性能影响的试验研究[J].建筑结构, 2013, 43(14): 77-82.

WU Xiaobao, LIN Feng, WANG Tao.Experimental research on effect of grout age and types of steel bars on mechanical behavior of grout sleeve splicing for reinforcing bars[J].Building Structure, 2013, 43(14): 77-82.