不同边界条件下高速旋转带篦齿薄壁短圆柱壳的行波共振特性研究
2018-05-25于晓光解志文
王 宇,于晓光,罗 忠,解志文
(1.辽宁科技大学 机械工程与自动化学院,辽宁 鞍山 114051; 2.东北大学 机械工程与自动化学院,沈阳 110819)
在航空发动机和汽轮机等动力旋转机械中,广泛使用着薄壁短圆柱壳构件,通常是指轴向半波数等于1,而且壁厚与其它最小特征尺寸(直径和长度)之比在1/80和 1/5 之间的圆柱壳体[1]。在许多实际薄壁壳体结构上, 还经常带有几何尺寸相对较小的周向篦齿结构, 例如航空发动机鼓筒上的封严篦齿环,很多情况下人们对其振动特性的研究需参考带加强肋的薄壁壳体研究。在此类结构服役过程中,很多振动疲劳损伤故障是由于外部复杂的工况和环境条件引起的共振造成的,对高速旋转带篦齿薄壁短圆柱壳的行波共振特性进行研究,判断构件发生共振时的转速、频率和振型之间的关系,具有重要的工程参考价值。
对于旋转态薄壁圆柱壳结构的振动问题,近年来具有代表性的研究成果如下:Sun等[2-3]基于Sanders壳体理论,采用波传播方法和傅里叶级数展开法,研究了转动薄壁圆柱壳的振动特性。李文达等[4]基于Sanders薄壳理论和Rayleigh-Ritz法,分析了弹性约束边界下旋转薄壁圆柱壳结构自由振动的行波特性。刘彦琦等[5]基于Love壳体理论和Galerkin方法,研究了不同边界条件下旋转薄壁圆柱壳的固有频率特性。在许多旋转圆柱壳构件上,经常带有周向篦齿结构,例如航空发动机鼓筒上的封严篦齿环,相关的研究结果主要有:Liu等[6]采用Rayleigh-Ritz方法,对任意边界条件下旋转态环加强圆柱壳的自由振动特性进行了分析。曾亮等[7]利用弹性力学和接触力学理论,采用动柔度法研究了静止时篦齿封严装置的振动特性。韩清凯等[8-9]利用传递矩阵法研究了旋转态薄壁圆柱壳及其带有篦齿结构时的固有振动特性。王洪玉等[10]针对航空发动机中鼓筒篦齿封严结构,采用数值方法对其流场进行了仿真分析,研究了旋转速度等因素的影响。相关的研究还可参阅李罡[11]、梁斌[12]、曹雷[13]和李辉[14]等学者的研究成果。对于高速旋转带篦齿结构薄壁短圆柱壳构件的行波共振特性,目前的研究相对较少,相关内容可参阅以下研究成果:王宇等[15-16]针对旋转态薄壁圆柱壳结构,对其共振特性和振动响应进行了分析。李波波等[17]采用有限元法分析了多转子串联轴系扭转振动的 Campbell 图以及临界转速等特性。田野等[18]采用有限元法研究了整体式转子和焊接式转子的临界转速,讨论了支撑和装配方式对临界转速的影响。王娇[19]研究了叶轮旋转机械中高速旋转叶片结构的共振特性。
因此,对于不同边界条件下高速旋转带篦齿薄壁短圆柱壳构件的行波共振特性,探讨结构发生共振时的转速、频率和振型之间的关系,以避免共振现象的发生,尚缺少相应的研究。本文基于Love壳体理论,在简支-简支、固支-固支、固支-简支、固支-自由和简支-自由五种边界条件下,采用传递矩阵法[20]对高速旋转带篦齿薄壁短圆柱壳的振动特性进行求解,对不同激振作用下的行波共振特性进行分析,为控制和避免动力旋转机械的共振问题具有实际意义。
1 旋转带篦齿薄壁短圆柱壳模型
旋转态带篦齿薄壁短圆柱壳的模型和断面形状如图1所示。在柱坐标系Oxθz中,原点O为端面上的圆心,圆柱壳以角速度Ω绕x轴转动,u(x,θ,t)、v(x,θ,t)和w(x,θ,t)分别为中面上任意一点在纵向、切向和径向三个方向上的位移,L,H和R分别为薄壁圆柱壳的长度、壁厚和中面半径;取篦齿断面为矩形,沿着轴向有2个篦齿,篦齿的高度为Hr、宽度为Lr、以间距Br等距离分布。

(a) 带篦齿薄壁圆柱壳模型

(b) 截面示意图图1 旋转态带篦齿薄壁短圆柱壳模型Fig.1 A model of rotating thin short cylindrical shell with two sealing teeth
2 不同边界条件下共振特性分析的传递矩阵法
如图1所示的带篦齿旋转态薄壁圆柱壳构件,可以沿着篦齿位置分成厚度相等的n0个区段(本文取n0=5),把每一个区段的圆柱壳视为一段光滑薄壁圆柱壳,且厚度相等。根据Love壳体理论[21],对于每一区段i(即:i=1, 2,…,n)的旋转薄壁圆柱壳,在纵向、切向与径向上的动力学微分方程为
(1a)
(1b)
(1c)

等效Kirchhoff面内切力Vx和横向剪力sx为
(2a)
(2b)
中面法线绕x轴的转角φx、内力Nx和内力矩Mx的表达式为
(3a)
(3b)
(3c)
令m表示轴向半波数,n表示周向波数,ω表示旋转圆柱壳的简谐振动圆频率,定义位移解的形式为
(4a)
(4b)
(4c)
式中:“+”和“-”分别表示转动坐标系中科氏力引起的后行波和前行波。
对于每一区段的圆柱壳,可以沿薄壁圆柱壳的纵向分为n0个子段,共n0+1个截面,任一截面上的状态向量为
(5)
在横断面上状态向量中的位移、转角、内力和内力矩表示为

(6)
(7)
将带篦齿薄壁圆柱壳构件分成n0个区段,对于某一区段的两个相邻截面,从一个端面至另一个端面的传递关系为
(8)
其中,对于每一区段薄壁圆柱壳的相邻两个截面,对应的传递矩阵关系为
(9)
在简支-简支、固支-固支、固支-简支、固支-自由简支-自由五种边界约束条件下,构件的前行波和后行波频率采用如下方法进行求解,即

(10)
令式(11)的系数行列式为零,可求得前行波和后行波的频率值,即
det(T′)=0
(11)

(12)

(13)

(14)

(15)
令fe为激振力频率,fmn表示轴向半波数为m和周向波数为n时的行波频率,当激振力频率与行波频率成如下关系时壳体结构将发生共振现象,即
fmn=N0·fe,N0=1, 2, 3, …
(16)
可以通过Campbell图判断高速旋转的构件是否会产生共振,其中射线表示激振频率,共振点对应的转速表示共振转速Nr,则激振频率为
fe=K·Nw
(17)
式中:K为谐波系数;Nw为工作转速,本文取Nw=2.5×104r/min。
当构件的转速发生变化时,在工作转速附近的共振转速比较危险,根据API标准,共振临界转速点应避开工作转速的±10%,通常用共振裕度来描述,其表达式为
(18)
3 算例分析
在简支-简支、固支-固支、固支-简支、固支-自由和简支-自由五种边界约束条件下,对高速旋转带篦齿Ti5Al2.5Sn钛合金[22]薄壁短圆柱壳的共振特性进行分析,在室温20℃时光滑薄壁圆柱壳构件的几何参数和材料参数如表1所示,取两个篦齿沿壳体长度方向均匀分布,篦齿的宽度Lr=0.004 m、高度Hr=0.002 m、篦齿间距为Br= 0.05 m,材料参数不变。

表1 薄壁圆柱壳构件的几何参数和材料参数Tab.1 Material and geometric parameters of a thin cylindrical shell
3.1 简支-简支边界条件
在转动坐标系和两端简支边界条件下,当转速为0 r/min时,采用传递矩阵法求得的带篦齿薄壁短圆柱壳的前六阶静频值如表2所示,并通过有限元程序ANSYS进行求解比较。由表2可知,通过两种方法得到的固有特性变化规律一致,最大频率误差为0.021%,第1阶固有频率对应(1,4)模态,随着静频值的增加,第2阶~第6阶对应的模态振型依次为(1,3)、(1,5)、(1,6)、(1,2)和(2,5),并且以周向模态的振动为主。

表2 简支-简支边界条件下带篦齿薄壁短圆柱壳的静频值Tab.2 The natural frequencies of the shell with sealing teeth for simple supported-simple supported boundary condition
当转速在0~3×104r/min时,取前六阶模态进行分析,对应的Campbell图如图2所示。当带篦齿薄壁短圆柱壳构件的转速逐渐增加时,由于科氏力影响引起了各阶模态对应的行波频率出现分离现象,并且后行波频率大于前行波频率。在3×104r/min转速范围内和K=1~6倍频激励作用下,与前六阶模态存在多个共振转速点,但在实际升速或降速过程中短时间通过时不会建立起共振工况。取工作转速为2.5×104r/min,行波频率线与激振频率线K=1和K=3~6的交点均远离工作转速,但是在工作转速附近容易引起共振的转速点仅有2个,即在K=2倍激振力作用下,与(1,2)阶和(1,6)阶模态形成共振,共振点频率分别为4 948 Hz和5 012 Hz,共振转速分别为23 620 r/min和23 930 r/min,与工作转速的共振裕度分别为5.52%和4.28%,而在其它交点处的共振裕度均大于10%,即壳体构件在共振转速下运行时很容易引起(1,2)阶和(1,6)阶模态的振动,并且共振裕度值越小越容易发生共振现象,即最容易引起共振裕度为4.28%的(1,6)阶模态的振动,应采取措施预先调整构件的工作转速、固有频率或激振频率,保证在工作转速时构件有充分的裕度,避免共振现象的发生。

图2 简支-简支边界条件下高速旋转带篦齿薄壁短圆柱壳的Campbell图Fig.2 A Campbell chart for a high-speed rotating thin short cylindrical shell with sealing teeth under simply supported-simply supported boundary condition
3.2 固支-固支边界条件
在转动坐标系和固支-固支边界条件下,带篦齿薄壁短圆柱壳构件的Campbell图如图3所示。当转速为0 r/min时,按照静频值从小到大的顺序,前6阶模态振型依次为(1,4)、(1,5)、(1,3)、(1,6)、(1,2)和(1,7),均表现为周向模态的振动。在3×104r/min转速范围内和K=1~6倍频激励作用下,与前六阶模态存在多个共振转速点,但在实际升速或降速等过程中短时间通过时不会建立起共振工况。当工作转速为2.5×104r/min时,行波频率线与激振频率线K=1和K=3~6的交点均远离工作转速2.5×104r/min,但是在工作转速附近容易发生共振的共振点有4个,即在K=2倍激振力作用下,与(1,2)阶和(1,6)阶模态形成共振,共振点频率分别为4 910 Hz、5 002 Hz、5 341 Hz和5 506 Hz,共振转速分别为23 450 r/min、23 880 r/min、25 500 r/min和26 290 r/min,与工作转速的共振裕度分别为6.2%、4.48%、2%和5.16%,在其它交点处的共振裕度均大于10%,即壳体构件在共振转速下运行时容易引起(1,2)阶和(1,6)阶模态的振动,共振裕度值越小越容易引起共振,即最容易引起共振裕度为2%的(1,6)阶模态的振动。
3.3 固支-简支边界条件
在转动坐标系和固支-简支边界条件下,带篦齿薄壁短圆柱壳构件的Campbell图如图4所示。
由图4可知,当转速为0 r/min时,按照静频值从小到大的顺序,前六阶模态振型依次为(1,4)、(1,3)、(1,5)、(1,6)、(1,2)和(2,5),以周向模态的振动为主。在3×104r/min转速范围内和K=1~6倍频激励作用下,与前六阶模态存在多个共振转速点,但在实际升速或降速等过程中短时间通过时不会建立起共振工况。当工作转速为2.5×104r/min时,行波频率线与激振频率线K=1和K=3~6的交点均远离工作转速2.5×104r/min,但是在工作转速附近容易发生共振的共振点有3个,即在K=2倍激振力作用下,与(1,2)阶和(1,6)阶模态发生共振,共振点频率分别为5 126 Hz、5 181 Hz和4 831 Hz,共振转速分别为24 650 r/min、24 740 r/min和23 070 r/min,与工作转速的共振裕度分别为1.4%、1.04%和7.72%,即壳体构件在共振转速下运行时容易引起(1,2)阶和(1,6)阶模态的振动,共振裕度值越小越容易引起共振,最容易引起共振裕度为1.04%的(1,2)阶模态的振动,而在其它交点处的共振裕度均大于10%。
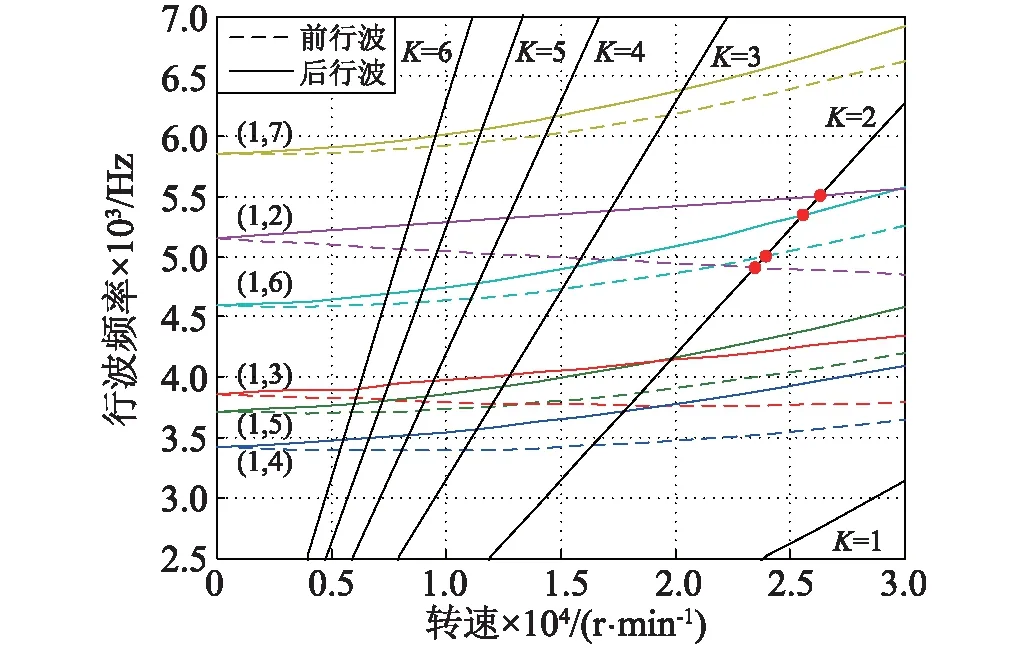
图3 固支-固支边界条件下高速旋转带篦齿薄壁短圆柱壳的Campbell图Fig.3 A Campbell chart for a high-speed rotating thin short cylindrical shell with sealing teeth under clamped-clamped boundary condition

图4 固支-简支边界条件高速旋转带篦齿薄壁短圆柱壳的Campbell图Fig.4 A Campbell chart for a high-speed rotating thin short cylindrical shell with sealing teeth under clamped-simply supported boundary condition
3.4 固支-自由边界条件
在转动坐标系和固支-自由边界条件下,带篦齿薄壁短圆柱壳构件的Campbell图如图5所示,当转速为0 r/min时,按照静频值从小到大的顺序,前六阶模态振型依次为(1,3)、(1,4)、(1,2)、(1,5)、(1,1)和(1,6),表现为周向模态的振动。在3×104r/min转速范围内和K=1~6倍频激励作用下,与前六阶模态存在多个共振转速点,在实际构件升速或降速等过程中短时间通过时不会建立起共振工况。当工作转速为2.5×104 r/min时,行波频率线与激振频率线K=2~6的交点均远离工作转速,但是在工作转速附近容易发生共振的共振点有2个,即在K=1倍激振力作用下,与(1,2)阶和(1,4)阶模态发生共振,共振点频率分别为2 432 Hz和2 547 Hz,共振转速分别为23 220 r/min和24 320 r/min,与工作转速的共振裕度分别为7.12%和2.72%,即壳体构件在共振转速下运行时容易引起(1,2)阶和(1,4)阶模态的振动,共振裕度值越小越容易引起共振现象,即最容易引起共振裕度为2.72% 的(1,4)阶模态的振动,而在其它交点处的共振裕度均大于10%。

图5 固支-自由边界条件高速旋转带篦齿薄壁短圆柱壳的Campbell图Fig.5 A Campbell chart for a high-speed rotating thin short cylindrical shell with sealing teeth under clamped-free boundary condition
3.5 简支-自由边界条件
在转动坐标系和固支-自由边界条件下,带篦齿薄壁短圆柱壳构件的Campbell图如图6所示。当转速为0 r/min时,按照静频值从小到大的顺序,前六阶模态振型依次为(1,4)、(1,5)、(1,6)、(1,3)、(2,6)和(1,2),以周向模态的振动为主。在3×104r/min转速范围内和K=1~6倍频激励作用下,与前六阶模态存在多个共振转速点,在实际构件升速或降速等过程中短时间通过时不会建立起共振工况。当工作转速为2.5×104r/min时,行波频率线与激振频率线K=1和K=3~6的交点均远离工作转速,但是在工作转速附近容易发生共振的共振点有2个,即在K=2倍激振力作用下,与(2,6)阶模态发生共振,共振点频率分别为5 108 Hz和5 457 Hz,共振转速分别为24 390 r/min和26 060 r/min,与工作转速的共振裕度分别为2.44%和4.24%,即构件在共振转速下运行时容易引起(2,6)阶模态的振动,而在其它交点处的共振裕度均大于10%,不易引起共振现象。

图6 简支-自由边界条件高速旋转带篦齿薄壁短圆柱壳的Campbell图Fig.6 A Campbell chart for a high-speed rotating thin short cylindrical shell with sealing teeth under simply supported -free boundary condition
4 结 论
本文基于Love薄壳理论和传递矩阵方法,在简支-简支、固支-固支、固支-简支、固支-自由和简支-自由五种边界条件下,分析了高速旋转带篦齿钛合金薄壁短圆柱壳构件的行波共振特性,主要结论如下:
(1) 当构件转速为0 r/min时,前六阶主要表现为周向模态的振动,在固支-自由边界条件下第1阶模态振动发生在(1,3)阶,其它四种边界条件下第1阶模态振动发生在(1,4)阶,边界条件不同时前六阶模态振型的分布规律也不同;在转速为0~3×104r/min范围内,随着构件转速的逐渐增加,由于科氏力作用引起了各阶模态对应的行波频率值出现分离现象,并且后行波频率大于前行波频率。
(2) 在3×104r/min转速范围内和K=1~6倍频激励作用下,激振频率线与前六阶模态存在多个共振转速点,在实际升速或降速过程中短时间通过时不会引起共振;在工作转速附近出现了共振裕度小于10%的共振转速点,边界条件不同时行波频率线与不同的激振频率线相交,在固支-自由边界条件下行波频率线与激振频率线K=1相交,而在其它四种边界条件下行波频率线与激振频率线K=2相交。
(3) 在五种边界条件下,在工作转速附近共振裕度小于10%的共振转速点数量和边界条件有关,在简支-简支、固支-自由和简支-自由三种边界条件下均出现2个共振转速点,而在固支-简支边界条件下有3个共振转速点,在固支-固支边界条件下有4个共振转速点,并且共振裕度值越小越容易引起对应阶次的共振现象,应采取措施调整构件的工作转速、固有频率或激振频率,保证在工作转速时有充分的裕度,避免共振现象的发生。
参 考 文 献
[1] 吴家龙.弹性力学[M].北京:高等教育出版社,2001.
[2] SUN S, CAO D, CHU S.Free vibration analysis of thin rotating cylindrical shells using wave propagation approach[J].Archive of Applied Mechanics, 2013, 83(4): 521-531.
[3] SUN S, CHU S, CAO D.Vibration characteristics of thin rotating cylindrical shells with various boundary conditions[J].Journal of Sound and Vibration, 2012, 331(18): 4170-4186.
[4] 李文达, 杜敬涛, 杨铁军, 等.边界条件对旋转薄壁圆柱壳结构自由振动行波特性的影响分析[J].振动工程学报, 2016,29(3): 452-464.
LI Wenda, DU Jingtao, YANG Tiejun, et al.Influence of boundary conditions on traveling wave characteristics of thin rotating cylindrical shell structure for free vibration[J].Journal of Vibration Engineering, 2016, 29(3): 452-464.
[5] 刘彦琦, 秦朝烨, 褚福磊.不同边界条件下旋转薄壁圆柱壳的振动特性[J].清华大学学报(自然科学版), 2012, 52(1): 5-9.
LIU Yanqi, QIN Zhaoye, CHU Fulei.Vibration characteristics of rotating thin cylindrical shells for various boundary conditions[J].Journal of Tsinghua University(Science and Technology), 2012, 52(1): 5-9.
[6] LIU L, CAO D, SUN S.Vibration analysis for rotating ring-stiffened cylindrical shells with arbitrary boundary conditions[J].Journal of Vibration & Acoustics, 2013, 135(6): 2627-2637.
[7] 曾亮, 李琳.用于篦齿封严装置的减振阻尼环设计理论[J].北京航空航天大学学报, 2007, 33(5): 518-522.
ZENG Liang, LI Lin.Design of damping-ring for vibration control in labyrinth air seals[J].Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(5):518-522.
[8] 韩清凯, 王宇, 李学军.旋转薄壁圆柱壳的高节径振动特性以及篦齿结构的影响[J].中国科学: 物理学力学天文学, 2013, 43(4): 436-458.
HAN Qingkai, WANG Yu, LI Xuejun.High nodal diameter vibration characteristics of rotating shell and the effects of its sealing teeth[J].Scientia Sinica Physica, Mechanica & Astronomica, 2013, 43(4): 436-458.
[9] 王宇, 韩清鹏, 李昌,等.篦齿对悬臂薄壁圆柱壳模态特性的影响研究[J].噪声与振动控制, 2015, 35(3): 82-86.
WANG Yu, HAN Qingpeng, LI Chang, et al.Influence of sealing teeth on the modal characteristics of a cantilever thin cylindrical shell[J].Noise and Vibration Control, 2015, 35(3): 82-86.
[10] 王洪玉, 秦朝烨, 褚福磊, 等.航空发动机直通型篦齿封严鼓筒气动力分析[J].工程力学, 2013, 30(12): 267-274.
WANG Hongyu, QIN Zhaoye, CHU Fulei, et al.Aerodynamic analysis of straight-through labyrinth seal of the drum of an aeroengine[J].Engineering Mechanics, 2013, 30(12): 267-274.
[11] 李罡,祝刚,何清军,等.带阻尼套筒的篦齿封严结构振型协调分析[J].机械强度, 2007, 29(1): 124-129.
LI Gang, ZHU Gang, HE Qingjun, et al.Vibration mode harmony analysis gas seals with damping sleeve[J].Journal of Mechanical Strength, 2007, 29(1):124-129.
[12] 梁斌, 李戎, 刘小宛, 等.基于波动法的静水压力下环肋圆柱壳耦合振动特性研究[J].振动与冲击, 2014, 33(21): 142-147.
LIANG Bin, LI Rong, LIU Xiaowan, et al.Coupled vibration of ring-stiffened cylindrical shells subjected to hydrostatic pressure using wave propagation method[J].Journal of Vibration and Shock, 2014, 33(21): 142-147.
[13] 曹雷, 马运义, 黄玉盈.基于Riccati传递矩阵法分析水下有限长环肋圆柱壳的声辐射性能[J].振动与冲击, 2009, 28(9): 149-154.
CAO Lei, MA Yunyi, HUANG Yuying.Analysis of acoustic radiation of a ring-stiffened cylindrical shell with finite length underwater based on Riccati transfer matrix method[J].Journal of Vibration and Shock, 2009, 28(9): 149-154.
[14] 李辉, 李其汉, 晏砺堂.某实际发动机篦齿封严装置振动特性和稳定性分析[J].航空动力学报, 2003, 18(1): 130-133.
LI Hui, LI Qihan, YAN Litang.Vibration character and aeroelastic stability analysis of real labyrinth gas seals[J].Journal of Aerospace Power, 2003, 18(1): 130-133.
[15] 王宇, 谷月, 李晖, 等.高速旋转薄壁圆柱壳的行波共振特性研究[J].振动与冲击, 2016, 35(5): 222-227.
WANG Yu, GU Yue, LI Hui, et al.Travelling wave resonance characteristics of a high-speed rotating thin cylindrical shell[J].Journal of Vibration and Shock, 2016, 35(5): 222-227.
[16] 罗忠, 王宇, 孙宁, 等.不同边界条件下旋转薄壁短圆柱壳的强迫振动响应计算[J].机械工程学报, 2015, 51(9): 64-72.
LUO Zhong, WANG Yu, SUN Ning, et al.Forced vibration response calculation of rotating short thin cylindrical shells for various boundary conditions[J].Chinese Journal of Mechanical Engineering, 2015, 51(9): 64-72.
[17] 李波波, 宾光富, 韩清凯, 等.基于有限元的多转子串联轴系扭转振动特性分析[J].湖南科技大学学报(自然科学版), 2014, 29(2): 31-35.
LI Bobo, BIN Guangfu, HAN Qingkai, et al.The method of multi-rotor tandem shafting torsional vibration characteristic analysis based on the finite element[J].Journal of Hunan University of Science & Technology(Natural Science Editon), 2014, 29(2): 31-35.
[18] 田野, 孙岩桦, 丁成伟, 等.不同支撑和转子装配方式的高速电机临界转速分析[J].振动与冲击, 2013, 32(8): 24-30.
TIAN Ye, SUN Yanhua, DING Chengwei, et al.Critical speeds of a high speed motor with different supports and rotor assembly[J].Journal of Vibration and Shock, 2013, 32(8): 24-30.
[19] 王娇.叶片阻尼结构的振动分析方法及其阻尼抑振效果研究[D].沈阳:东北大学, 2013.
[20] 王宇.薄壁圆柱壳的振动特性及其篦齿结构影响研究[D].沈阳:东北大学, 2014.
[21] LI H, LAM K Y, NG T Y.Rotating shell dynamics[M].Elsevier, 2005.
[22] 《中国航空材料手册》编辑委员会.中国航空材料手册[M].北京: 中国标准出版社, 2002.
