一种高聚类无标度网络中的混合路由策略*

徐玉珠

（民航贵州空管分局，贵州 贵阳 550002）

0 引 言

现实生活中与人们息息相关的互联网、交通网、生物神经网、通信网络、电力网络和社交关系网等大型网络，都可以被模拟构建成复杂网络的模型。在复杂网络的研究历史上，Watts和Strogatz提出了“小世界网络”。该模型反映了很多复杂网络平均路径短且聚类系数高的小世界特征。之后，Barabási和Albert建立的“BA无标度网络”，揭示了复杂网络中节点的度具有幂律分布的特性，即无标度性质。但是，现实生活中的网络几乎同时具备这两种网络的特性，因此建立一个高聚类无标度网络十分必要[1-2]。

以现实通信网络为例，网络中超负荷的流量常常导致网络拥塞的产生。良好的传输能力和较大的网络吞吐量，能够保证网络运行通畅，而较差的传输能力和较小的网络吞吐量会严重影响网络运行的通畅。目前，可知的影响网络传输能力和吞吐量的因素主要有两个。一是网络结构性因素，如网络的拓扑结构、节点间的连接方式、节点的处理能力和通信带宽等。若是通过改变网络的结构性因素提高网络传输能力，通常比较困难。例如，对Internet网络中的某两个路由器增加一个连接，需要在它们之间铺设一条通信线路，费用可能非常昂贵，且实际铺设不一定能够实现，所以这样的方式不现实。另一个是路由选择策略因素。一个合理的路由选择策略可以极大地提高网络的传输能力和吞吐量，且采用良好的路由方案也较为可行。所以，在研究网络拥塞问题、传输能力问题及吞吐量问题方面，目前通常针对路由策略进行研究[3]。

基于上述思想，本文在BA网络基础上，考虑加入社团结构，并考虑边的演化存在于新旧节点同时也存在于旧节点之间，以此建立改进的BA网络，使之更贴近于现实网络。同时，以改进的模型为平台，建立了一种混合信息路由策略。结合最短路径路由算法和优化的传递概率模型，把节点的介数作为其传递信息的能力，通过对可调参数的调节，提高路由效率，有效缓解网络拥塞[3]。

1 新增社团结构网络优化模型的构建及仿真分析

1.1 网络模型的构建

Barabási和Albert建立的BA网络模型中，节点的度具有幂律分布特性，但整个网络的聚类系数很低。现实生活中，网络往往遵循高聚类，且节点度为幂律分布。因此，建立一个高聚类无标度的网络模型十分必要。相比其他网络模型，BA网络具有网络规模可增长和节点加入优先选择连接的优势。但是，网络模型的增长仅仅考虑了单一新节点的加入。类比于现实社会网络，某个成员加入网络后，往往意味着和该成员相关的一个社团都成为网络的一个新成员[4-5]，且BA网络中新边的产生只存在于新节点和旧节点之间。实际上，这种边的演化机理也同时存在于旧节点之间。基于上述思想，提出的改进网络模型在网络特性方面增大了BA网络的聚类系数。在网络增长方式上，使加入网络的节点情况从单一节点加入变为社团结构的加入，同时使网络新边增长存在与新旧节点和旧节点之间[5]。

改进模型演化机理如下。

（1）初始网络：m0个完全连接的节点构成网络的初始模型。

（2）网络增长：按照概率p(∈[0,1])，网络中加入一个含有n个节点的小型社团网络结构和m条新边。

随机选择新加入社团结构中一个节点v，并按照择优概率选择网络中一个旧节点与节点v相连，使新加入节点v与网络中的旧节点之间具有一条边。连接节点的选择按照如下的择优概率进行，即网络中一个旧节点i被选择的概率(ki)为[5-6]：

其中，ki为节点的度。这个择优概率选取的连接机制代表新节点的加入更倾向于与网络中度较大的节点相连接。α为可调因子，其中α∈(0,1)。因为所加入的社团结构为全连接，所以当社团中一个节点被加入网络后，其余的(n-1)个节点也同时被加入到网络。

其余(m-1)条边，以概率(ci)做三角形连接，1-(ci)做择优概率，其中：

（3）网络内部演化：按照概率1-p选择网络中现有的节点做网络内部演化。随机选择网络中一个节点i，以择优概率选择节点i的邻居节点j，其中连接概率按照如式（3）选择：

其中，（N(i)为选中旧节点i的邻居节点集合），再以概率1-(ci)选择节点j的邻居节点k与节点i做连接。

当概率p=0时，网络中无新社团结构的加入，没有新节点增长机制，网络的增长仅发生在旧节点之间，然后旧节点之间进行内部演化加边。当0＜p＜1时，每个时间步长，网络中既可能有新社团的加入，增加网络的节点与边，也有网络的内部演化加边，即随着p的增加，网络中社团结构的增长机制所占比重越来越大。当概率p=1时，网络中旧节点之间不进行内部演化加边，每个时间步长有一个新社团加入网络。然而，概率p=1的情况在现实网络中通常不会出现[7]。

1.2 仿真结果及分析

设定固定参数，网络初始节点数m0=4，每次新增社团结构节点连接边的数目m=3，可调因子α=1，网络规模N=1 000。通过模拟实验研究选择概率p对网络中节点度分布的影响，实验结果如图1所示。

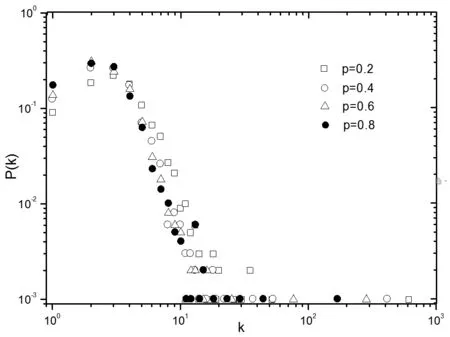
图1 p取不同值时，改进模型的度分布

由图1可知，改进模型继承了BA模型度分布遵循幂律分布的特点。由于选择概率p的不同取值，幂律分布的指数可以进行调节，打破了BA网络中节点度分布幂律指数固定的限制。

设定固定参数，网络初始节点数m0=4，每次新增社团结构节点连接边的数目m=3，选择概率p=0.4，网络规模N=1 000。通过模拟实验研究概率α对网络中节点度分布的影响，实验结果如图2所示。

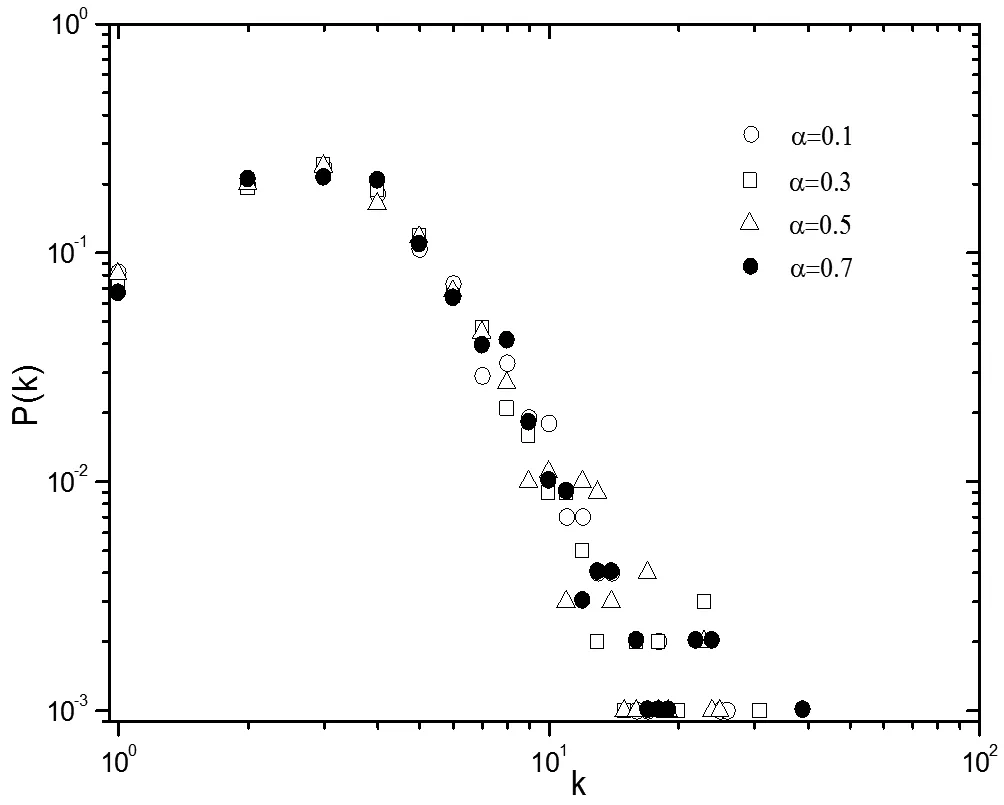
图2 α取不同值时，改进模型的度分布

由图2可知，可调参数α取不同值时，网络节点度分布始终服从幂律分布，且幂律指数由参数α可调，更灵活，更符合实际网络。

设定固定参数，网络初始节点数m0=4，每次新增社团结构节点连接边的数目m=3，可调因子α=1，网络规模N=1 000。通过模拟实验研究选择概率p对聚类系数的影响，实验结果如图3所示。

改进模型由于选择概率p的不同取值，网络聚类系数也不同。由图3可知，p=0.2时，网络中节点聚类系数平均值约为0.45；p=0.4和p=0.8时，网络中节点的聚类系数平均值约为0.49；而p=0.6时，网络聚类系数平均值最大，约为0.52。相比BA网络无明显聚类效应而言，改进的网络聚类系数大大提高了。

可调参数α取不同值时，改进模型的聚类系数分布也不相同，如图4所示。由图4可知，α=0.1和α=0.5时，网络中节点聚类系数平均值约为0.47；α=0.7时，网络中节点的聚类系数平均值约为0.48；而α=0.3时，网络聚类系数平均值最大，约为0.51。相比BA网络无明显聚类效应而言，改进的网络聚类系数被大大提高了。

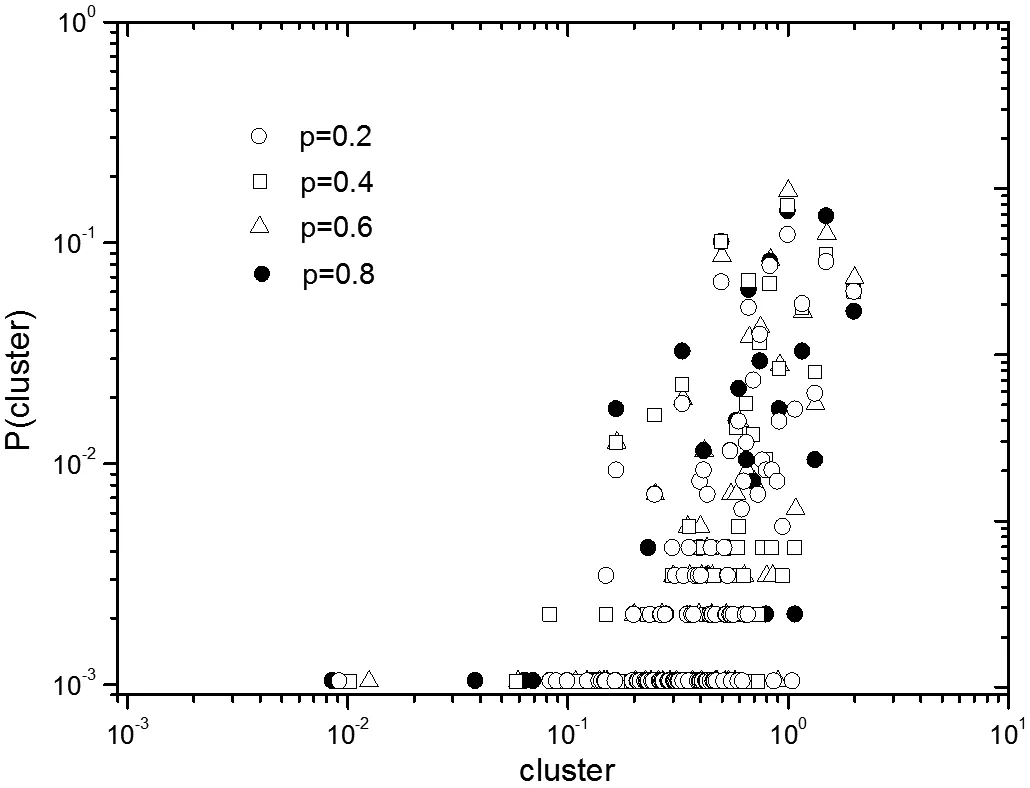
图3 p取不同值时，改进模型的聚类系数分布

图4 α取不同值时，改进模型的聚类系数分布

综合考虑，在构建改进BA网络模型时，选择概率p设定为0.6，可调参数α设定为0.3。这种情况下构建的网络模型，度分布保持幂律分布，且整个网络的聚类系数很高，符合现实网络特性。本文研究的混合信息路由策略以此改进模型为平台。

2 基于混合信息的路由策略

为了使网络模型更真实地反应现实网络，本文采用初始网络中节点个数为5、网络规模N=1 000的新增社团结构网络优化模型为实验的基础模型。

具体路由算法如下：

（1）在网络中，每个时间步长产生R个数据包。随机选取数据包的起始节点和数据包最终需要到达的目的节点。起始节点和目的节点选定后则不更改，且两个节点不能相同。网络中，每个节点可以作为产生数据包的起始节点、接收数据包的目的节点，也可以作为传递数据包的中间节点[8]。类比于现实生活的互联网，网络中每个节点可以是产生或接收信息的服务器，又可以是传递信息的路由器。

（2）假设每个节点的传递能力为该节点的介数。实际网络中，度越大的节点在网络中越重要，习惯上也把度较大的节点称作网络中心节点。这样的节点更有能力处理大量的信息包，因此很多现有的路由策略将节点的数据包传递能力设定为该节点的度，即在一个时间步内能处理的数据包个数等于该节点度的大小，或将节点传递信息包的能力正比于节点的度。理论上，路由策略的作用是缓解拥塞节点的负载，而网络节点的介数才是用来表示网络相对负载的，且介数比度更能精确反应节点的中心特性[8-9]。因此，本文假设每个节点的传输能力为Oi（Oi为节点i的介数），即在一个时间步内，节点处理的数据包个数等于该节点介数的大小。取消节点传递能力固定的限制，能更好地反映实际网络的特征。

（3）遍历当前数据包所在节点的所有邻居节点，若目的节点存在于邻居节点，则直接将数据包传递给目的节点；否则，以概率1-p选择传统最短路径路由策略。以概率p做优先选择，择优概率为[10]：

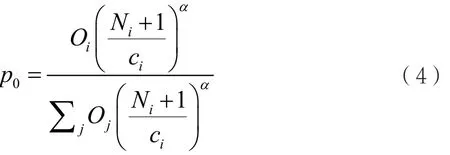
以此概率传递给下一个节点。其中，α是一个可调的参数，Ni是结点i的排队队列长度，Ni+1是为了保证邻居节点中空闲节点被选中的概率不为0。

（4）本文的路由策略假设每一节点处排队的数据包个数可以为无限个，排队等候的数据包依次传递时需要遵从先进先出（FIFO）的原则[11]，且任何节点只能被同一个数据包访问一次。

网络性能可以通过利用整个网络对信息包的处理和传递能力进行衡量。为了更准确地描述网络状

该算法中的有序参数η(R)为网络中数据包总量的变化率，即在数据包生成率为R的情况下，每个时刻网络中数据包总量的增长速率，有时也用H(R)表示。O是网络中节点传递能力的平均值。其中，ΔW=W(t+Δt)-W(t)，W(t)表示t时刻网络中数据包的总个数，ΔW则表示在Δt时间内网络中数据包个数的改变量。当R＜RC时，数据包的产生率小于临界负载量，η(R)大约等于0，t时间长度内网络中数据包个数无变化，产生与到达的数据包个数相互抵消，使网络中每个时间步长稳定的数据包个数低于临界负载量，网络处于无拥塞状态；当R＞RC时，数据包产生率大于负载量，η(R)＞0，有序参数为一个大于0的常数，t时间长度内产生的数据包个数远大于到达的数据包个数，网络中的数据包总量累计增加，促使网络变为拥塞状态。所以，η从0到大于0常数的突变，可以得出网络从自由状态转变为拥塞状态[13]。态变化，设定每个时间步长，网络中随机产生R个数据包（即数据包的生产率为R，有时也用来表示），临界信息负载量RC。RC是整个网络从自由态到拥塞态的变化的临界值。当R＜RC时，每个时间步长，网络中新增的数据包个数小于网络的临界负载量，网络状态为自由通畅状态；当R=RC时，每个时间步长，网络中产生的数据包个数恰好等于网络的临界负载量，网络通信能力达到临界值，为最大通信能力；当R＞RC时，每个时间步长，网络中产生的数据包个数大于网络的临界负载量，网络状态为拥塞状态。所以，RC为使得网络处于无拥塞状态时的最大值，即网络传输容量。同时，本文也利用参数η(R)来描述该网络状态的变化[12]：

3 仿真结果及分析

3.1 路由效率分析

优先选择概率中，α为可调参数。不同的搜索策略值α下，网络的通信能力不同。图5表明，不同α下，每个时间步长，网络中产生的数据包个数对η的影响。可以看出，每个时间步长，产生数据包的个数小于临界负载量。R＜RC时，η为0；当新增数据包个数超过临界负载量R＞RC时，η骤变成大于0的常数；R=RC时，网络通信量达到临界值。可见，α取不同值时，临界负载量RC不同，即网络的最大通信量不同。

图5 不同α时，η的参数统计

对α取不同值时的网络临界负载量做统计，如图6所示。当α=0.2时，网络临界负载量达到最大值，RC=250。所以，本实验中α的值取0.2。

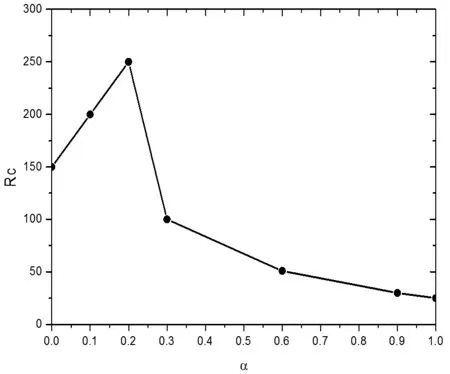
图6 不同α时，RC的参数统计

改进的路由策略规定，路由选择时，以概率1-p选择传统最短路径路由策略，并以概率p做优先概率选择。图7为固定参数α=0.2，p取不同值时，网络产生数据包个数对η的影响。同样，由图7可知，每个时间步长，产生数据包的个数小于临界负载量时，η为0；当产生数据包个数超过临界负载量RC时，η骤变为大于0的常数。

对p取不同值时的网络临界负载量RC做统计，由图8可知，p取0.2时，路由效率最高，临界负载量RC=300，则实验设p=0.2。

3.2 网络自由态分析

网络的自由通畅状态是指，网络中每个时间步长产生的数据包个数能够和网络中被移除的数据包个数相互抵消，使网络中每个时间步长稳定的数据包个数低于或等于网络临界负载量，网络即处于通畅状态[14]。设定R=40，R小于不同α取值时RC的平均值。由图9可知，初始时间段内，数据包个数累计增长；经过一段时间的积累，数据包的个数达到稳定，即产生和移除的数据包个数达到平衡，网络处于通畅稳定状态，即自由态。可以得出，α=0.2时，随时间的增加，网络中数据包总数稳定在200左右，效率最佳。从图10也可得出，α=0.2时，η最稳定，为最趋近于0的常数。

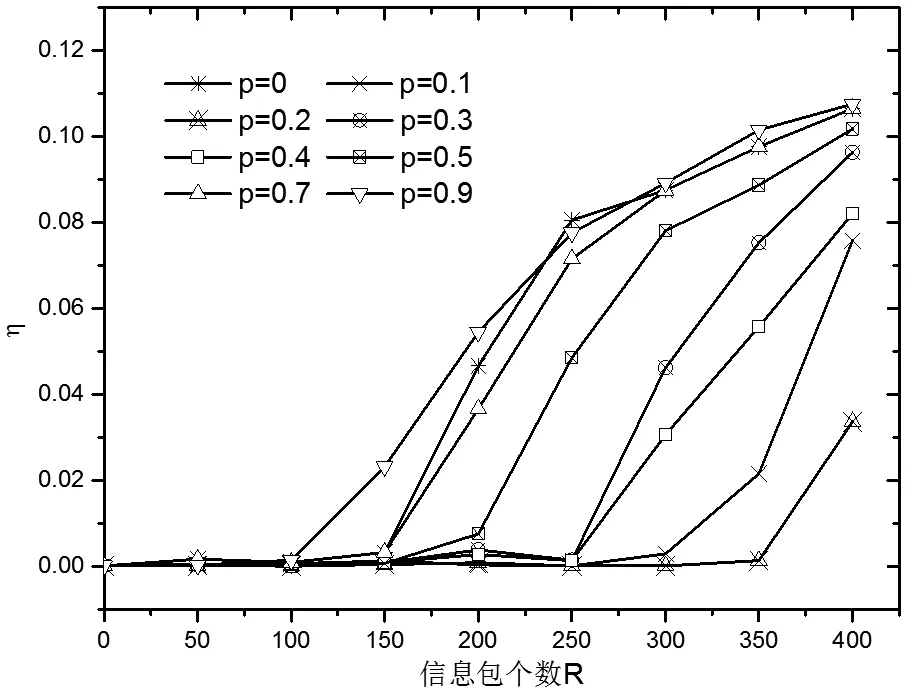
图7 不同p时，η的参数统计

图8 不同p时，RC的参数统计

3.3 网络拥塞态分析

网络的拥塞状态是指，每个时间步长产生的数据包个数与网络中被移除的数据包个数无法完全相互抵消，导致网络中总体数据包个数持续累计，最终稳定的数据包个数高于临界负载量，导致网络拥塞。设定R=500，R大于不同α取值时RC的平均值。由图11可知，随着时间的增加，网络中数据包的个数累积增长，无趋于稳定状态的趋势，导致大量数据包滞留于网络，使得网络处于拥塞状态甚至崩溃。图12表明，拥塞状态下，η一直为大于0的常数。

图9 R＜RC时，不同α下网络数据包变化情况

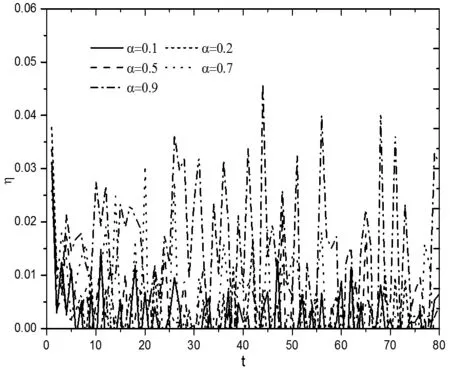
图10 R＜RC时，不同α下η变化情况

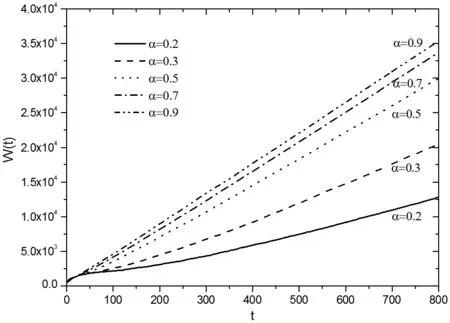
图11 R＞RC时，不同α下网络数据包变化情况

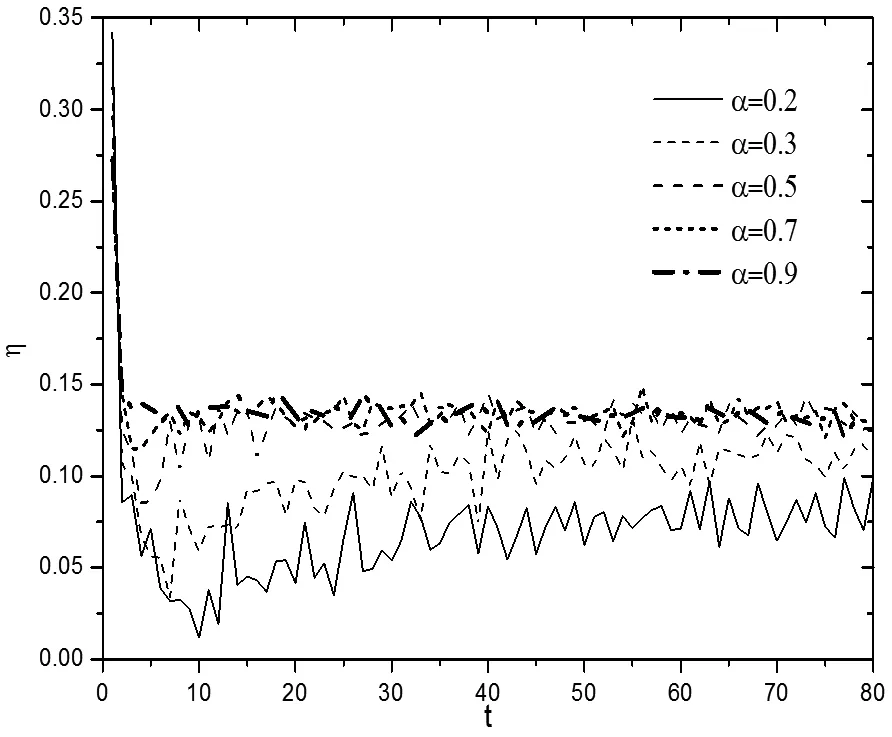
图12 R＞RC时，不同α下η变化情况

4 结 语

针对现实世界中很多大规模的网络都同时具有小世界与无标度网络特性，在传统BA网络的演化机制中加入“内部演化”“新增社团”演化机制，建立改进的高聚类无标度网络模型，同时在新建模型的基础上，提出了一种混合信息路由策略，将节点的传递能力设定为节点的介数而不是一个固定值。路由选择时，以概率1-p选择传统最短路径路由策略，以概率p做优先选择，并提出了优先选择概率模型。仿真实验表明，混合路由策略可以显著提高网络路由的效率。实验中，通过对选择概率

p和可调参数α的调节得出最优组合，即p=0.2，

α=0.2时，在合理设置数据包产生率的情况下，可以有效缓解网络的拥塞。

参考文献：

[1] 王翠君,王红.复杂网络的研究进展综述[J].科技信息 ,2007,31(31)：417-418.WANG Cui-jun,WANG Hong.Summary of Research Progress on Complex Networks[J].Science,2007,31(31)：417-418.

[2] 徐玉珠,张达敏,曾成等.改进HK网络演化模型的研究 [J].电子科技 ,2016,29(03)：106-109.XU Yu-zhu,ZHANG Da-min,ZENG Cheng,et al.Research and Modeling of the Improved HK Network Model[J].Electronic Science and Technology,2016,29(03)：106-109.

[3] 刘倩星,张达敏.基于混合信息的复杂网络路由策略研究[J].计算机工程与设计,2012,33(03)：880-884.LIU Qian-xing,ZHANG Da-min.Routing Strategy Research Based on Mixed Information in Complex Networks[J].Computer Engineering and Design,2012,33(03)：880-884.

[4] 王丹,金小峥.可调聚类系数加权无标度网络建模及其拥塞问题研究[J].物理学报,2012,61(22)：543-551.WANG Dan,JIN Xiao-zheng.On Weightd Scale-free Network Model with Tunable Clustering and Congesstion[J].Acta Physica Sinica,2012,61(22)：543-551.

[5] 王丹,郝彬彬.一类高聚类系数的加权无标度网络及其同步能力的分析[J].物理学报,2013,62(22)：1-8.WANG Dan,HAO Bin-bin.A Weighted Scale-free Network Model with High Clustering and Its Synchronizability[J].Acta Physica Sinica,2013,62(22)：1-8.

[6] 濮存来,裴文江.一种应用于含权无标度网络的全局路由算法[J].物理学报,2010,59(06)：3841-3844.PU Cun-lai,PEI Wen-jiang.A Global Routing Method for Weighted Scale-free Networks[J].Acta Physica Sinica,2010,59(06)：3841-3844.

[7] 蒋忠元.复杂网络传输容量分析与优化策略研究[D].北京：北京交通大学,2013.JIANG Zhong-yuan.Analysis and Optimization Strategies of Traffic Capacity of Complexnetworks[D].Beijing：Beijing Jiaotong University,2013.

[8] 潘灶烽,汪小帆.一种可大范围调节聚类系数的加权无标度网络模型[J].物理学报,2006,55(08)：4058-4064.PAN Zao-feng,WANG Xiao-fan.A Weighted Scale-free Network Model with Large-scale Tunable Clustering [J].Acta Physica Sinica,2006,55(08)：4058-4064.

[9] 李稳国,王力虎,陈明芳.HK网络演化模型的研究和改进[J].计算机工程,2009,35(03)：121-125.LI Wen-guo,WANG Li-hu,CHENG Ming-fang.Study and Improvement on Growing HK Network Model[J].Computer Engineering,2009,35(03)：121-125.

[10] 刘建香.复杂网络及其在国内研究进展的综述[J].系统科学学报 ,2009,17(4)：31-37.LIU Jian-xiang.Complex Network and Review of Domestic Research[J].Chinese Journal of Systems Science,2009,17(04)：31-37.

[11] 胡海波,王科,徐玲等.基于复杂网络理论的在线社会网络分析[J].复杂系统与复杂性科学,2008,5(02)：1-14.HU Hai-bo,WANG Ke,XU Ling,et al.Analysis of Online Social Networks Based on Complex Network Theory[J].Complex Systems and Complexity Science,2008,5(02)：1-14.

[12] 王丹,井元伟,郝彬彬.扩展HK网络结构与同步能力的研究[J].物理学报,2012,61(22)：1-8.WANG Dan,JING Yuan-wei,HAO Bin-bin.Extended Holme-Kim network model and synchronizability[J].Acta Physica Sinica,2012,61(22)：1-8.

[13] Galstyan A,Musoyan V,Cohen P.Maximizing Influence Propagation in Networks with Community Structure[J].Physical Review E,2009,79(345)：314-319.

[14] Barabási A L,Albert R.Emergence of Scaling in Random Networks[J].Science,1999,286(286)：509-512.