一种基于射影平面的高维等角紧框架*

朱 皓，唐川雁

（杭州电子科技大学 通信工程学院，浙江 杭州 310018）

0 引 言

在稀疏码分多址技术（SCMA）中，发送端稀疏码本的设计直接决定了可获得的系统性能增益，同时也决定了接收机设计的复杂程度。框架是一种类似正交基的序列集合，但是其元素之间是线性相关的，具有一定的冗余性。相比正交基对于元素表示的唯一性，框架的使用更为灵活。近年来，随着框架理论的研究与发展，它在量子信息理论、压缩感知和代数编码理论等领域得到了广泛应用[1-4]。框架理论中，等角紧框架（Equiangular Tight Frame，ETF）是一种具有良好相关特性的框架，每个框架元素都有很低的峰均功率比（Peakto-Average Ration，PAR），使框架元素间的互相关度达到了最小，十分适用于SCMA。但是，现有的ETF构造方法十分有限[5]，无法得到满足SCMA要求的高维码本。因此，本文阐述等角紧框架的基本概念，介绍了射影和仿射平面的相关知识，提出了一种基于仿射平面的高维等角紧框架构造方法，并用此方法构造了一个19维空间中包含76个向量的复数等角紧框架，解决了实数框架无法实现的难题。

1 框架及等角紧框架

对于 Hilbert空间的一组序列 {φj}j∈J，如果存在常数A和B满足0＜A,B＜∞，使对于所有f∈H，满足不等式：

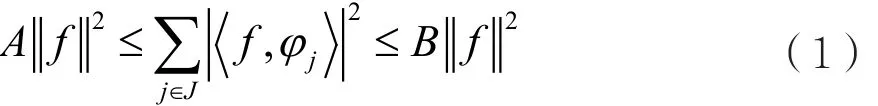
则称{φj}j∈J为空间H的一个框架，A和B为其上下界。设F是实数或者虚数域，H是F中d维实数或者复数希尔伯特内积空间，{φj}j∈J是H中任意非零单位范数框架，它的合成算子Φ为Fn→Hd，n≥d。若存在a＞0满足ΦΦ*=aI，则该框架为紧框架。若对于框架中所有向量有||φi||2=r，r＞0，说明这是单位范数框架。若单位范数框架中任意向量间存在|〈φi,φj〉|=w，i≠j，则该框架为等角框架。如果{φj}j∈J即是等角框架又是紧框架，那么该框架为等角紧框架。

{φj}j∈J的最大互相关度可定义为：

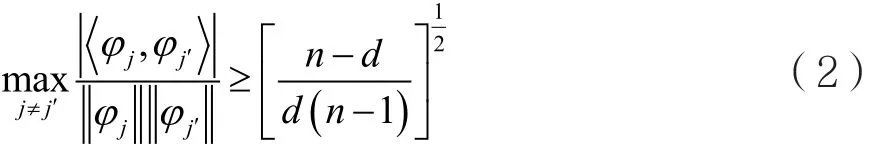
当{φj}j∈J为等角紧框架时，框架的最大互相关度满足Welch界[6]，即式（2）中等号成立。

2 有限射影和仿射平面

在平衡不完全区组（BIBD）中，有限集V由v个处理组成。B是V的子集，它由b个区组组成，存在正整数λ、k、r满足：

（1）每个区组都包含k个处理；

（2）每个处理恰好存在于r个区组中；

（3）任意一对处理恰好存在于λ个区组中。

当满足：

其中，大小为b×v的矩阵X是一个BIBD关联矩阵。这里1表示全1向量，J表示全1矩阵。根据v、k、λ，可以得到r、b：

这种关联结构通常被称为2-(v,k,λ)，表示为BIBD(v,k,λ)。

当BIBD中λ=1时，可以得到斯坦纳等角紧框架，这也意味着两个不同的处理决定一个唯一的区组。实际上，这种BIBD典型例子是有限仿射和射影平面，即BIBD(q2,q,1)和BIBD(q2+q+1,q+1,1)，q≥2。当q=2时，可以分别得到以下关联矩阵X：

定义1[7]：假设X为BIBD(v,k,1)的一个b×v关联矩阵。对于任意j=1,…,v对应的嵌入（embedding）是Ej:Fr→Fb，即Fr的标准基映射为Fb中r维子空间的标准基。

对于任意BIBD(v,k,1)和幺模单形{sl}r+1l=1，对应的斯坦纳等角紧框架就是{Ejsl}vr+1j=1,l=1。这里，v(r+1)个向量组成一个等角紧框架[7-8]，它们的合成算子为：

Φ=[E1S…EvS] （6）

对于一个BIBD(q2,q,1)，如果假设r-k=1，那么任何处理若不存在一个区组中，那么一定恰好存在于一个不相交区组中。这意味着如果区组i和i'不相交，且i'和i''也不相交，那么i与i''相等或者不相交。当两个区组不相交或者相等时，这两个区组平行，因此平行性是仿射平面上区组的一个等价关系。这说明任意仿射平面是可解析的，即它的区组集合B可以表示成不相交的子集集合{Br}r∈R。例如，式（5）中的二阶仿射平面就是可解析的，第1、2行，第3、4行，第5、6行分别形成了B的一个子集。正因为仿射平面可解析，所以q阶仿射平面均可扩展成q阶的射影平面。

射影平面是对称BIBD，即v=b。通常，BIBD(v,k,λ)是通过交换处理和区组的角色或者取其关联矩阵的转置X的转置得到的关联结构。通过式（4）可以推出，同时通过式（3）推出的列是标准正交的。当BIBD对称时，这个矩阵是方阵且它的行也必定正交，这意味着XXT=(k-λ)I+λJ。因此，对称BIBD(v,k,1)的对偶是另一种BIBD(v,k,1)。所以，任何射影平面的对偶也是另一种射影平面。

定理1：当q为素数幂时，一定存在q阶仿射和射影平面正则构造。

证明：假设Fq是包含q个元素的域，使V=F2q，B为这个向量空间所有仿射线的集合，组成一个仿射平面，即：

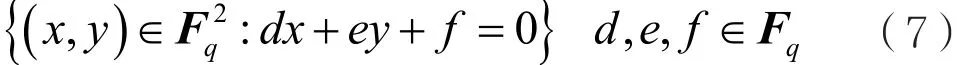
其中(d,e)≠(0,0)，f为变量。处理和区组分别对应Fq3中一维和二维子空间。

使[x,y,z]表示所有非零标量集乘一个非零向量(x,y,z)∈Fq

3。为了形成射影平面，需使V成为所有[x,y,z]的集合，使B成为这种构造的集合：

映射(x,y)↦[x,y,1]将正则仿射几何嵌入到这个射影几何中：对于任意(d,e)≠(0,0)的[d,e,f ]，式（8）是在此映射条件下对式（7）的映像。这里，将等同为域Fq3的加法群，α为循环乘法群的生成集合，且使 (x,y,z):=x+yα+zα2,x,y,z∈ Fq。因为每个[x,y,z]包含所有非零标量乘非零向量(x,y,z)，所以这是商群唯一的元素。

3 基于仿射平面构造高维等角紧框架

归纳总结文献[8-9]中的斯坦纳等角紧构造方法，可以得到新的复数等角紧框架构造方法。对于任意e≥1，d维复数希尔伯特空间中n个向量组成的等角紧框架满足：

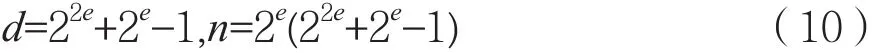
q阶射影平面上的椭圆是q+2个处理的集合，此时不存在3个处理位于同一公共区组上，即不存在3个对应的向量线性相关。比如，式（5）中2阶射影平面前4个处理（列）是一个椭圆，因为没有区组（行）同时包含其中3个处理。椭圆将射影平面分解成其他几个关联结构。

引理1：如果一个q阶射影平面包含一个椭圆，那它必定有如下相关矩阵：

X1,1是BIBD(q+2,2,1)的关联矩阵，这里X1,1的列对应椭圆中的处理，q为偶数，且XT2,2是的关联矩阵。

证明：假设一个BIBD(q+2,2,1)包含u个特殊处理，它们不能3个同时存在于一个区组中，关联矩阵X的前u列对应这些特殊的处理。这种特殊的处理-区组（vertex-block）对的数量为：

同时，每个不同特殊处理的对决定了唯一的区组，所以：

当u=q+2时，式（13）中等式成立，即所有特殊的处理-区组对都在包含2个特殊处理的区组中，也就是说当射影平面包含一个椭圆时，存在处理和区组的枚举。所以，X1,1是BIBD(q+2,2,1)的关联矩阵。通过式（4）可以得到X1,1大小为(q2-1)。由于射影平面的对偶是另一个射影平面，所以XXT=qI+J，那么X,=qI+J，从而推出

2,2的关联矩阵。

当q为素数的幂时，存在q阶射影平面，而当射影平面包含椭圆时，q需要为偶数，那么q=2e，e≥1。对于q=2e阶正则射影平面，它的正则椭圆为：

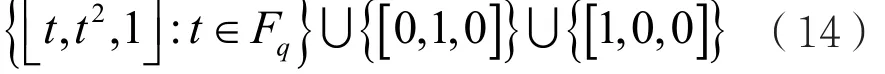
引理2：如果一个q阶射影平面包含一个椭圆，那么它的对偶存在关联矩阵：

其中Y1,1是(q+2,2,1)。将Y中最后q+2行中任意一行和最后q+1列移除，就会产生一个q阶仿射平面，它存在关联矩阵：是BIBD

其中是BIBD(q+1,2,1)的关联矩阵。

证明：取引理1中给出分解出的转置式，交换其行和列可以得到式（15）。将Y中单个区组（行）与它包含的q+1个处理（列）移除，可以得到一个q阶仿射平面。选出最后q+2个区组中的其中一个，移除Y2,2中一行和q+2个列，移除0中的一行，移除Y1,2中q+1个列并保留Y1,1不变，即可得到式（16）。因为Y2,2的列表示q+2行，Z2,2的列表示剩余的q+1行，所以ZT2,2表示BIBD(q+1,2,1)的关联矩阵。

例如，式（5）中的2阶射影平面包含椭圆，因为它形如式（11）。先将其转置，然后排列行和列，能得到形如式（15）射影平面的7×7的关联矩阵：个幺模元素，所以||Ejsl||2=||sl||2=q+1。

因为每个Ej都是一个等距且{sl}lq+2是幺模单形，所以|〈Ejsl,Ejsl'〉|=|〈sl,sl'〉|=1，l≠l'；同理，|〈Ejcl,Ejcl'〉|=|〈cl,cl'〉|=1，l≠l'。而当j≠n'时，会出现不同内积：

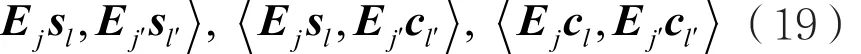
第二个矩阵是一个形如式（16）仿射平面的关联矩阵。这是第一个矩阵移除第4行和第2、3、4列得到的。

定理2：对于一个含有椭圆的q阶射影平面，假设是由形如式（16）的仿射平面中产生的嵌入，假设和分别为Fq+1的幺模单形和幺模协单形，则有：

在设计的BIBD中任意两个不同区组正好有一个共同的处理，这意味着Ej中某一列正好是Ej'的某一列，这时Ej是Fr中两个标准正交元素的外积，即，有：

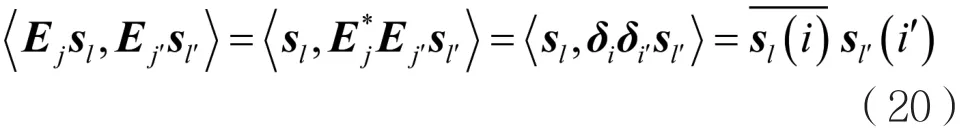
同理，可以得到式（19）中另外两个内积是。因为每个sl和cl的元素都为幺模数，所以这些内积都为单位模量，满足等角紧框架的构造条件。

这是Fq(q+1)的q2+q-1维子空间中一个由q(q2+q-1)个向量组成的等角紧框架。

证明：当n=q(q2+q-1)，d=q2+q-1时，Welch界

4 实验结果

根据定义1可知，每个Ej都是一个等距（isometry），即Ej=I。因为每个sl和cl都含q+1

图1是一个19维空间中包含76个向量的复数等角紧框架，满足式（10），即n=76，d=19。为了提高可读性，用字母表的前10个字母分别表示5×6的幺模单形和5×4的幺模协单形的行。

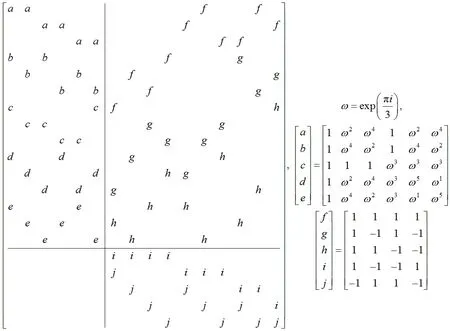
图1 一个复数等角紧框架

参照引理2，从4阶射影平面上的椭圆中分解出一个仿射平面，然后利用这个仿射平面将6个单形和14个协单形插入到C20中去。前36个向量形成了文献[9]中的C15斯坦纳等角紧框架，后40个向量是实数。通过用加法群Fq3=F64=Z2(α)定义，从而构造了一个q=22=4的射影平面，其中α是Z2中多项式β6+β+1的根[10]。射影平面上的处理集合为V= =〈 αα〉//〈αα2211〉≅ZZ2211，利用式（14）中的处理 {t+t2α+α2:t∈ F4}∪ {1}∪ {α}，取其对数基α得到椭圆{0,1,2,3,5,14}。这个椭圆提供了形如式（11）的21×21关联矩阵。置换它的对偶，得到一个形如式（15）的矩阵。去掉该椭圆其中一行及其对应的列，就能得到形如式（16）的20×16仿射平面。最后，验证可知该框架为等角紧框架。

5 结 语

在SCMA系统中，设计一个好的码本可以在不增加功率和频带利用率的条件下降低系统误码率。等角紧框架元素间有最低的互相关度，非常适合组建系统的扩频码本。但是，如今构造高维等角紧框架十分困难。因此，本文提出了一种基于射影平面的等角紧框架构造方法，可以有效构造出高维等角紧框架，在实际SCMA扩频码本的组建中具有重要价值。

参考文献：

[1] 曲长文,何有,刘卫华等.框架理论及其应用[M].北京：国防工业出版社,2009：116-175.QU Chang-wen,HE You,LIU Wei-hua,et al.Framework Theory and Applications[M].Beijing：National Defense Industrial Press,2009：116-175.

[2] Renes J M,Blume-Kohout R,Scott A J,et al.Symmetric Informationally Complete Quantum Measurements[J].Journal of Mathematical Physics,2003,45(06)：2171-2180.

[3] Bernardini R,Rinaldo R.Oversampled Filter Banks from Extended Perfect Reconstruction Filter Banks[J].IEEE Transactions on Signal Processing,2006,54(07)：2625-2635.

[4] Balan R,Casazza P G,Edidin D.On Signal Reconstruction without Phase[J].Applied and Computational Harmonic Analysis,2006,20(03)：345-356.

[5] Fickus M,Mixon D G.Tables of the Existence of Equiangular Tight Frames[J].Mathematics,2015,436(05)：1014-1027.

[6] Strohmer T,Heath R W.Grassmannian Frames with Applications to Coding and Communication[J].Applied and Computational Harmonic Analysis,2003,14(03)：257-275.

[7] Fickus M,Jasper J,Mixon D G,et al.Tremain Equiangular Tight Frames[J].Journal of Combinatorial Theory,2018(153)：54-66.

[8] Fickus M,Mixon D G,Tremain J C.Steiner Equiangular Tight Frames[J].Linear Algebra and its Applicatio ns,2012,436(05)：1014-1027.

[9] Jasper J,Mixon D G,Fickus M.Kirkman Equiangular Tight Frames and Codes[J].IEEE Transactions on Information Theory,2014,60(01)：170-181.

[10] Hansen T,Mullen G L.Primitive Polynomials over Finite Fields[J].Mathematics of Computati on,1992,59(200)：639-643.