基于对称压缩MUSIC的相干源方位估计方法*

徐 姝，梁仕杰

（江苏科技大学 电子信息学院，江苏 镇江 212003）

0 引 言

在实际环境中，相干源的存在是DOA估计技术不可避免的问题。当前，比较经典的MUSIC、ESPRIT等空间谱算法，都是基于信源相互独立的前提下提出的。当存在相关或强相干信源时，对于相干源的DOA估计将会失效。为了能够获得相干源的方位信息实现解相干，学者们提出了许多解相干算法。其中，最常见的解相干方法包括最大似然法[1]、Toeplitz矩阵重构法和空间平滑法[2-6]等。最大似然方法是一种能够有效解相干的方法，原理是利用概率密度模型对相干源数据进行处理。但是，为了获得较好的解相干性能，此种算法需要通过多维非线性搜索来获得DOA估计。由此可见，此种算法计算量相当大。Toeplitz矩阵重构法也是当前常用的一种解相干方法，优点是不存在孔径损失，但估计性能较差，针对孔径为代价来实现解相干。鉴于以上问题，空间平滑类解相干算法得以大力发展，成为解相干类算法的一个重点研究方向。

不过，空间平滑类算法属于降维算法，本质是以牺牲阵列的有效孔径为代价。为此，Pillai等对空间平滑类算法进行了改进，提出了一种双向平滑类算法，即前后平滑法。前后平滑法是将整个阵列看作一个子阵进行平滑，本质上是不存在有效孔径损失的，但将阵列看作一个子阵进行前后平滑，最多只能分辨2个相干源信号。Kundo D[7]将前后平滑运用到经典的MUSIC算法上，虽然可以得到精度高的分辨能力，但是在对多个相关信源的分辨上，性能大幅下降。Zhang[8]等对传统的MUSIC算法加以改进，提出了一种特征子空间MUSIC算法（Eigen Space MUSIC，ES-MUSIC），即在原有的MUSIC算法基础上充分利用信号子空间，大幅提高了抗噪性能，且相对于传统MUSIC算法明显提升了估计精度和分辨率，已被许多专家学者加以改进并应用[9-12]。上述算法由于数据协方差的处理和谱搜索的运算量使得算法复杂度大幅提高，难以运用到实际工程。为此，有必要提出一种既可以解相干又可以减少计算量的算法来实现DOA估计。

本文针对传统平滑技术以损失阵列有效孔径为代价获得解相干能力和空间谱搜索计算量大的缺点，提出一种新的平滑技术。此平滑技术充分利用互协方差矩阵来构建一个新的协方差矩阵，然后获得信号子空间、噪声子空间，并引入对称压缩谱（MUSIC Symmetrical Compressed Spectrum，MSCS）思想[13]，利用导向矢量与噪声子空间的双重正交性等效添加镜面辐射源，构造对称压缩谱函数。实验证明，本文算法大大减少了空间谱搜索计算量，且在一定程度上提高了算法的抗噪性能和分辨率。

1 MUSIC算法

假设有M元均匀线阵，阵元间距为d，在远场波导条件下有k个窄带信号源以平面波入射，入射角度为 θ，θ={θ1,θ2,…θK}，则其阵列接收信号的模型可以表示为：

式中X(t)为M×1数据矢量，N(t)为M×1阶加性高斯白噪声，S(t)为信号矢量，即：

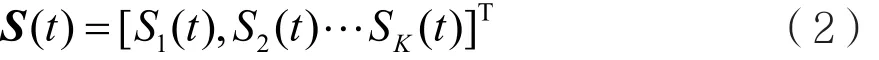
A(θ)为阵列流行矩阵，即：

式中，a(θi)称为信号的导向矢量：

假设在每个阵元的噪声是零均值的高斯白噪声，且相互独立时矢量阵接收数据的协方差矩阵为R，则R可由式（5）求得：

其中：

理想条件下，信号子空间与噪声子空间相互正交。所以，信号的阵列流型与噪声子空间也相互正交，即：

然而，在实际环境下，由于快拍数、信噪比等条件限制，使得导向矢量不可能与噪声子空间绝对正交。Schmidt利用这个特性构造了经典MUSIC算法空间谱：

再对式（8）进行谱搜索，其谱峰位置点处即为其波达角。

2 本文算法

2.1 互协方差矩阵的平滑算法

平滑技术是解相干的一种常见技术，本文在传统的前后平滑的基础上加以改进提出一种最大限度利用数据互协方差矩阵来构建新的协方差矩阵的方法，从而使得算法的抗噪声性能，以及分辨率得以提升。此方法不需要牺牲阵列有效孔径便可以获得较好的解相干能力。

假设对式（1）进行如下变形：

其中X*(t)表示为X(t)的复共轭；J为M×M维置换矩阵，其副对角线上元素均为1，其余各元素均为0，即：

很明显，J*J=I，I为单位矩阵，进而可以求得Y(t)的协方差矩阵：

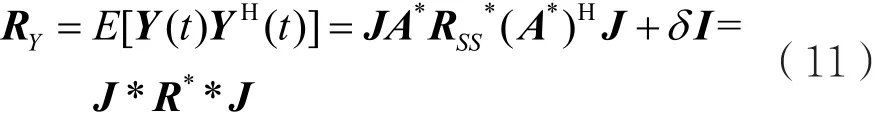
以此类推，可以求得Y(t)和X(t)的协方差矩阵为：

最后，令：

则可求得需要的协方差矩阵为：

理论上，若只考虑X(t)、Y(t)信号自协方差矩阵，会使那些无用的信号累加，增加了估计误差，降低了算法的估计性能。用到的互协方差矩阵利用了两个不同的信号之间的相乘，则这2个信号减去均值的信号存在共性部分和非共性部分。共性部分相乘时取相同的符号，使该部分得到了加强而保留下来；非共性部分则是随机的，它们的乘积有时取正有时取负，利用数学期望进行平均运算后趋于相互抵消。也就是说，可以利用互协方差矩阵提取2个信号的共性部分，并且抑制掉非共性部分，然后再与X(t)、Y(t)信号的自协方差矩阵求平均，得到更具有平均意义的R～。所以，该算法的抗噪声性能和分辨率得以提升。基于这个优点，可以将该方法与对称压缩谱相结合。

2.2 MSCS算法

假设空间存在一信源P，其到均匀线阵的信号为窄带远场信号，设其到达角度为θ1。根据欧拉公式，利用奇函数的性质，对导向矢量a(θ1)取共轭，可得：

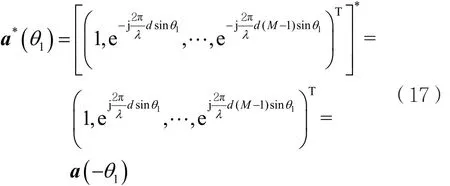
根据Schmidt所提的正交性原则，可得：

对式（18）的左右两边进行共轭处理，可以得到：

对式（19）左右两边同时取共轭，可得：

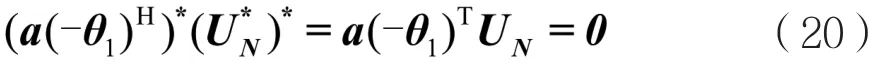
由此可知，信源P的y轴对称区间存在一镜面信源P'，且两者入射角度互为相反数。所以，两者所对应的导向矢量呈复共轭关系。若前者的导向矢量与UN相互正交，则后者的导向矢量与U*N相互正交。根据此特性，可以将MUSIC算法空间谱进行对称压缩，从而构建新的空间谱函数：

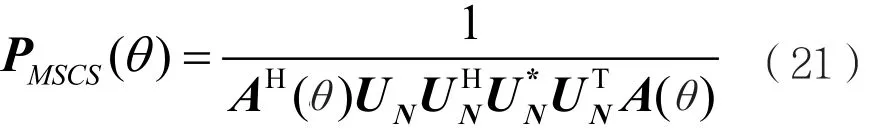
对式（21）在[-90° 0°]或者[0° 90°]进行谱搜索，得到谱峰位置后，再将谱峰对应的方位角度代入||aH(θ)UN|| ≈ 0判别是否成立。如果成立，便得到真实信源；反之，即为镜面信源。

2.3 本文算法流程

（1）利用互协方差矩阵构造新的协方差矩阵式（16）；

（2）对式（16）求得的协方差矩阵进行分解，得到 R～=USΛSUSH+UNΛNUNH，求得噪声子空间；

（3）根据对称压缩谱原理构造空间谱函数：

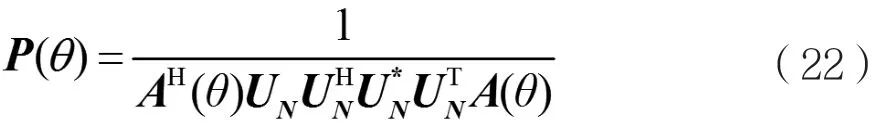
（4）在[-90° 0°]或者[0° 90°]进行谱峰搜索得到方位信息；

（5）带入 ||aH(θ)UN|| ≈ 0进行判别，成立得到真实信源，反之即为镜面信源。对镜面信源取反，即可得到全部的波达角。

3 仿真

3.1 算法性能对比

将本文算法与MSCS算法进行对比，设3个信源的入射角度分别为-10°、30°、60°，其中-10°与30°为相干信源，入射到阵元数为18阵元间距λ/2的均匀线阵，信噪比为-5 dB，快拍数为100，搜索步长为1°,搜索范围为[-90°90°]，仿真图如图1所示。由图1可以看出，原本的MSCS算法解相干源时已经失效，而本文算法在-10°对应的正半轴10°,在30°、60°所对应的负半轴-30°、-60°也会形成等幅度的谱峰，说明本算法具有有效性。

图1 本文算法与MSCS算法空间谱

将本文算法与空间前向平滑算法进行对比，设3个信源的入射角度分别为-10°、30°、60°，其中-10°与30°为相干信源，入射到阵元数为18阵元间距λ/2的均匀线阵，子阵阵元数为17，子阵个数为2，信噪比为-5 dB，快拍数为100，搜索步长为1°,搜索范围为[-90° 90°]，仿真实验图如图2所示。图2中相比于前向平滑算法，本文算法旁瓣压制得更低，谱峰更加尖锐，说明本文算法的抗噪声性能更好。同时可以看出，在实际的相干源方位估计应用时，本文算法只需要在[-90° 0°]或者[0° 90°]搜索即可得到完整的方位信息，大大降低了搜索量。

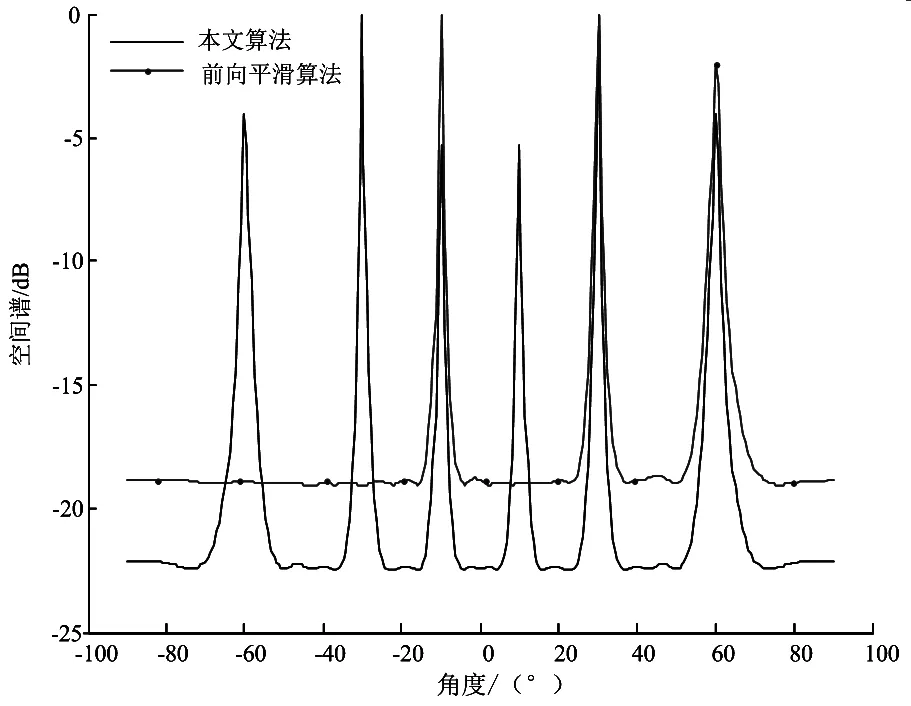
图2 本文算法与前向平滑算法空间谱

设3个信源的入射角度分别为-10°、30°、60°，其中10°与30°为相干信源，入射到阵元数为18阵元间距λ/2的均匀线阵，子阵阵元数为17，子阵个数为2，信噪比为-5 dB，快拍数为100，搜索步长为1°，搜索范围为[0° 90°]，仿真图如图3所示。将半谱范围内得到的10°、30°、60°方位信息带入||aH(θ)UN|| ≈ 0进行判别，30°、60°满足判别公式为真实信源，10°不满足判别公式为镜面信源，取反操作得到10°。完成上述判别操作后，即可得到全部的波达角为10°、30°、60°。

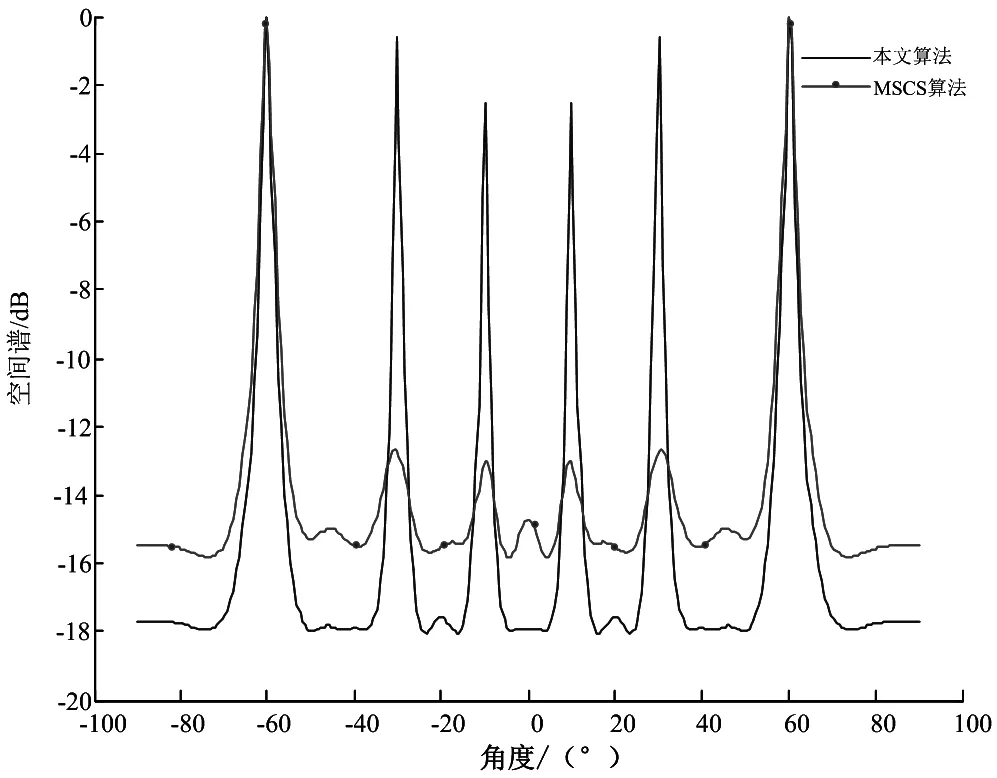
图3 本文算法在半谱内搜索

3.2 两种算法成功率对比

阵元数为18的均匀线阵，子阵阵元数为17，子阵个数为2，将入射角度设置为10°、30°、60°，其中10°与30°为相干信源，取信噪比从-10 dB，按照-2 dB的间隔增加至10 dB，快拍数取20、50、100，进行100次独立计算机仿真实验。当偏差在0.5°内认定算法成功，即成功率定义为成果次数与总实验次数的比值，仿真结果如图4所示。

图4 3种快拍下2种算法的成功率

由图4可知，在信噪比一定时，2种算法的成功率随着快拍数的增加而提高。整体来看，本文所提算法在相同信噪比和快拍数下，本文算法的成功率优于前向平滑算法。

3.3 两种算法标准差分析

阵元数为18的均匀线阵，子阵阵元数为17，子阵个数为2，将入射角度设置为10°、30°、60°，其中10°与30°为相干信源，取信噪比从-10 dB，按照-2 dB的间隔增加至10 dB，快拍数取20、50、100，进行100次独立计算机仿真实验，仿真结构如图5所示。由图5可知，在信噪比一定时，2种算法的标准差随着快拍数的增加而降低。从整体来看，本文所提算法在相同信噪比和快拍数下，本文算法的标准差优于前向平滑算法。

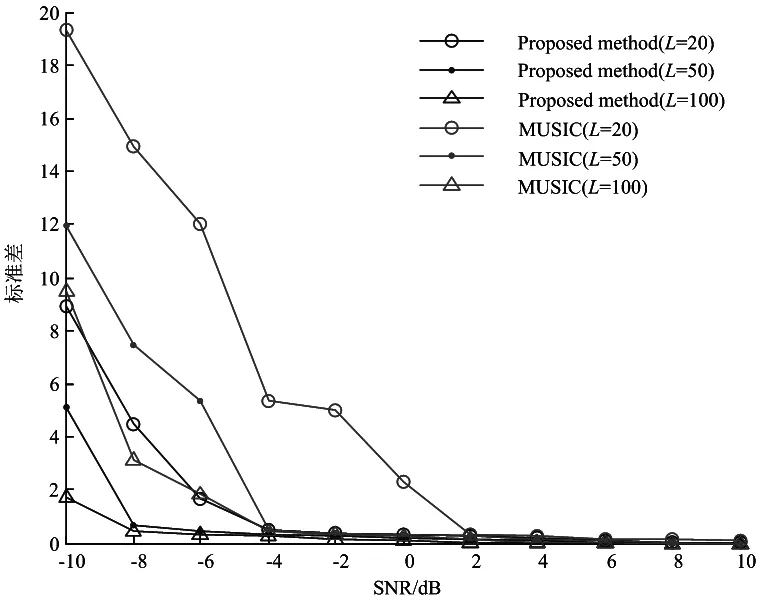
图5 3种快拍下2种算法的标准差

4 结 语

本文针对传统的多重子空间分类算法不适用于相干源条件且谱搜索计算量大的问题，在传统的前后平滑算法基础上，最大限度利用数据互协方差矩阵来构建新的协方差矩阵，提高了算法抗噪性能和分辨率。对协方差矩阵进行特征值分解，利用对称压缩谱思想，构造一种新的空间谱函数，即可在半谱范围内进行谱搜索得到完整的方位信息，大大减少了空间谱搜索的计算量。因此，本文算法具有重要的现实意义。

参考文献：

[1] Stoica P,Arye N.Music,MaximumLikelihood,and Cramer-Rao Bound[J].IEEE Transactions on Acoustics Speech and Signal Procession,1989,373(05)：720-741.

[2] Evans J E,Johnson J R,Sun D F.High Resolution Angular Spectrum Estimation Techniques for Terrain Scattering Analysis and Angle of Arrival Estimation[C].Processing 1st ASSP Workshop Spectral Estimation,Hamilon,Ontario Canada,ASSPWSE,1981：134-139.

[3] Shan T J,WAX M,LAILATHT.On Spatial Smoothing for Estimation of Coherent Signals[J].IEEE Transactions on Acoustics Speech and Signal Processing,1985,33(04)：806-811.

[4] 陈文锋,陈桂清.基于空间平滑MUSIC算法的相干信号DOA估计[J].计算机应用与软件 ,2017,34(11)：232-235+283 CHEN Wen-feng,CHEN Gui-qing.Coherent Signal DOA Estimation Based on Spatial Smoothing Music Algorithm[J].Computer Applications And Softwa re,2017,34(11)：232-235,283

[5] Todros K,Hero A O.Robust Multiple Signal Classification Via Probability Measure Transformation[J].IEEE Transactions on Signal Processing,2015,63(05)：1156-1170.[6] Zhang W,Liu W,Wang J,et al.Joint Transmission and Reception Diversity Smoothing for Direction Finding of Coherent Targets in MIMO Radar[J].IEEE Journal of Selected Topics in Signal Processing,2014,8(01)：115-124.

[7] Kundu D.Modified MUSIC Algorithm for Estimating DOA of Signals[J].Signal Processing,1996,48(95)：85-90.

[8] Zhang X F,Lv W,Shi Y,et al.A Novel DOA Estimation Algorithm Based on Eigen Space[C].IEEE International Symposium on Microwave,Antenna,Propagation and EMC Technologies for Wireless Communications,2007：551-554.

[9] 刁鸣,丁兆明,高洪元等.基于特征空间算法的非圆阵相干信源DOA估计[J].哈尔滨工程大学学报 ,2014(12)：1559-1563.DIAO Ming,DING Zhao-ming,GAO Hong-yuan,et al.DOA Estimation of Non-circular Coherent Sources Based on Eigenspace Algorithm[J].Journal of Harbin Engineering University,2014(12)：1559-1563.

[10] 熊轶.基于特征子空间的波达方向(DOA)估计算法研究[D].武汉：华中科技大学,2007.XIONG Yi.Research on DOA Estimation Algorithm Based on The Eigen-subspace[D].Wuhan：Huazhong University of Science and Technology,2007.

[11] 崔波,罗景青.最小冗余线阵的ES-DOA估计算法研究 [J].信号处理 ,2010(07)：1016-1020.CUI Bo,RUO Jing-qing.Study on ES-DOA Estimation Algorithm of Minimum-Redundancy Linear Arrays[J].Signal Processing,2010(07)：1016-1020.

[12] 程乃平,倪淑燕.改进的特征空间波束形成算法[J].通信学报 ,2010(S1)：32-36.CHENG Nai-ping,NI Shu-yan.Modified Eigenspacebased Beamforming Algotithm[J].Journal on Communications,2010(S1)：32-36.

[13] 闫锋刚,刘帅,金铭等.基于MUSIC对称压缩谱的快速DOA估计[J].系统工程与电子技术 ,2012,34(11)：2198-2202.YAN Feng-gang,LIU Shuai,JIN Ming,et al.Fast DOA Estimation Based on MUSIC Symmetrical Compressed Spectrum[J].Systems Engineering and Electroni cs,2012,34(11)：2198-2202.