基于离群点检测和分类的软测量方法

王春鹏

(中海油石化工程有限公司，山东 济南 250001)

1 在线离群点检测方法

1.1 支持向量数据描述(SVDD)算法理论

Tax等人提出的支持向量数据描述(SVDD)是解决单值分类问题的有效方法，SVDD是一种基于支持向量机学习的算法；通过一个非线性映射函数，把数据从输入空间映射到一个高维空间，寻找支持向量在特征空间中，构造包围与最小半径和超球体的最佳点[1]。超球体的描述模型目标类是由支持向量，超球外点被判定为离群点的数据不属于目标类(也称为离群点)确定。以二维空间为例的超球体示意如图1所示。

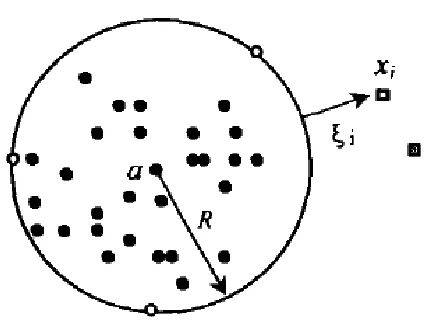
图1 超球体示意图

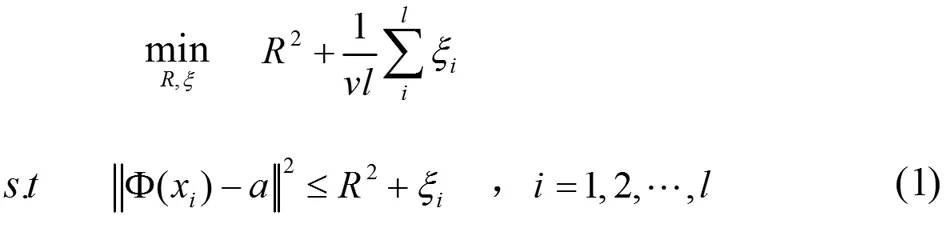
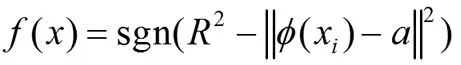
加入拉格朗日乘子αi,βi≥0，将原来的问题(1)可以转化称无约束的问题(2)：

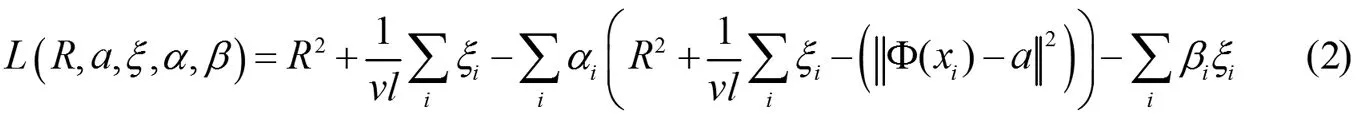
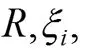
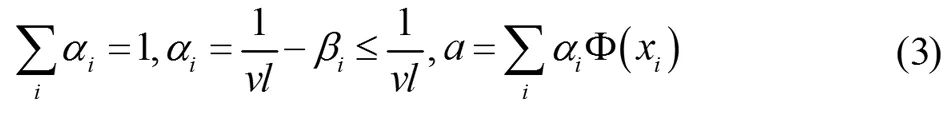
把(2)表示为对偶问题，并引入核函数来取代特征空间上的内积运算得：

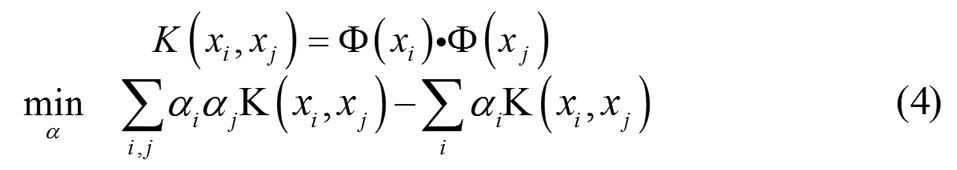
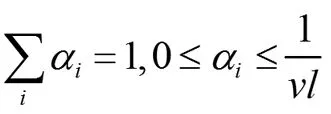
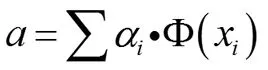
1.2 在线支持向量数据描述参数更新

当模型在实际运行中，如果发生过程的变化，如汽油干点软测量中精馏塔的原油发生变化，那么测量的数据也会发生变化超出我们检测判断的正常范围。因此，SVDD的参数半径和球心也得随着数据的变化而变化，这样才能适应过程的变化而不会导致误判正常数据为离群点。

本文针对这个过程引入了指数加权移动平均(EWMA)这种鲁棒的方式来更新SVDD参数，指数加权移动平均的公式如下：

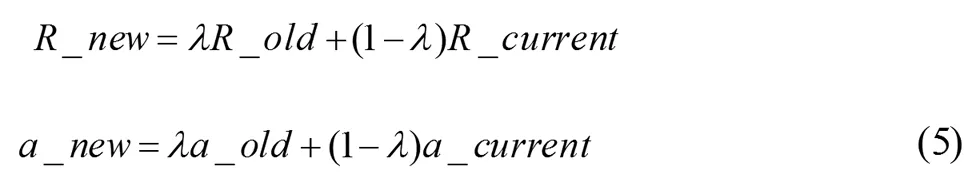
R_old和a_old代表着更新前离群点检测的判断参数，R_new和a_new代表着更新后离群点检测的判断参数，R_current和a_current是用一定量新的样本所构成的离群点检测参数。λ为更新因子代表着参数更新的速度。

对一个正常的过程，譬如没有连续检测出大量离群点，更新因子我们通常设定为0.7<λ<0.9。而当连续检测出大量的离群点时更新因子我们通常设为0.01<λ<0.05。

2 在线离群点分类方法

贝叶斯分类器是一种基于统计方法的典型的分类模型，它是基于贝叶斯理论，先验概率和后验概率被巧妙地联系在一起，利用先验信息和样本数据来确定所述事件的后验概率[2-3]。

采用贝叶斯分类原理对以检测到的离群点进一步分类，分类过程如图2 所示。

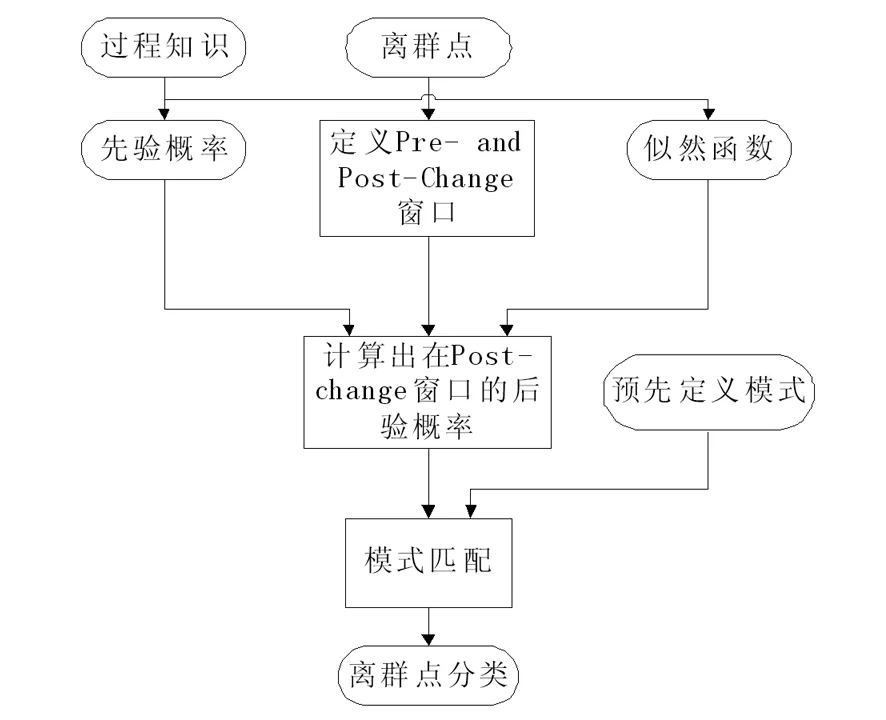
图2 贝叶斯对离群点的分类过程

2.1 长阶跃数据的判断准则

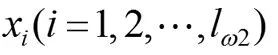
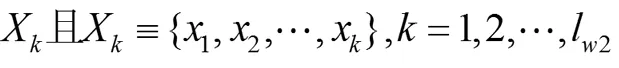
为了表示在x1点发生阶跃，我们定义置信限C1，则需要满足：

仅仅依靠公式(7)我们还不能判断此时发生的阶跃是不是长阶跃，因为还有可能是脉冲或者短阶跃。因此，我们还需要Post-ChangeWindow中更多的数据来证明。由于我们假设阶跃发生在Post-ChangeWindow的开始，所以随着样本数目的增加，后验概率也单调递增：

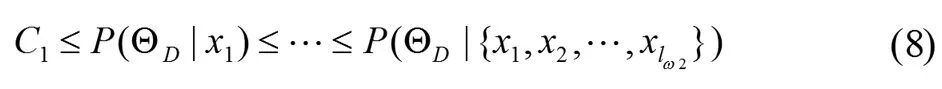
为了提高对长阶跃信号检测和分类的精确性，我们需要让整个Post-ChangeWindow的后验概率比置信限C2要大：

方程(6)～(9)用来作为判断长阶跃的准则，一般情况下C1取0.8，C2取0.99，本文也是取这个值。

2.2 脉冲数据的判断准则

对于脉冲信号的干扰，在Post-ChangeWindow中的第一个值x1提供了脉冲信号的幅值。这是和阶跃信号所不同的，阶跃信号需要很多数据一起才能确定。因此，对于脉冲干扰μD=x1。为了确定脉冲干扰，我们首先需要满足：

C1为置信限，x1满足N(μD,σ2)分布。

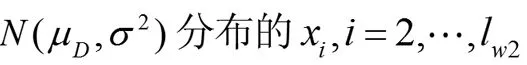
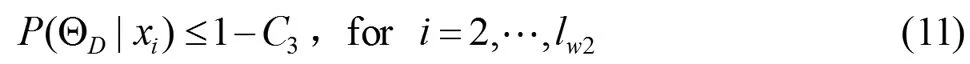
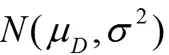
2.3 短阶跃数据的判断准则

根据上面讲的长阶跃和脉冲干扰的知识，我们很容易确定对短阶跃信号的处理。短阶跃的幅值μD是对每个Post-ChangeWindow的子集来计算的。同样的，在Post-ChangeWindow中的第一个值x1应满足：

因为我们假设干扰是短阶跃，在Post-ChangeWindow中短阶跃持续阶段的后验概率必须满足和长阶跃一样的关系：

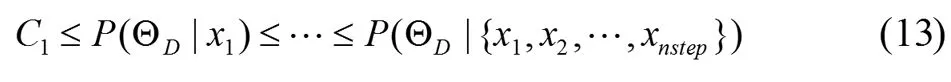
和式(9)一样，在Post-ChangeWindow中短阶跃持续阶段的后验概率必须大于一个置信限C2：

最后，为了指出短阶跃干扰结束，在Post-ChangeWindow后的短阶跃的后验概率必须小于一个阈值，和式(14)对脉冲干扰一样：

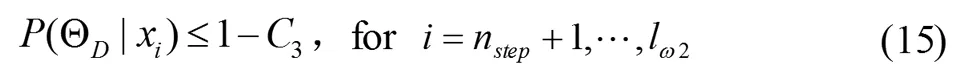
方程(13)-(15)就是判断短阶跃的准则。

3 仿真研究

为了验证所给出的算法的有效性，我们针对化工过程中常用的软测量技术进行仿真研究，本文采用某炼化厂航空煤油的干点数据进行研究仿真。

首先离线进行离群点的检测，把检测到的离群点排除掉然后利用PLS-RBF进行离线建模作为软测量模型[4]，然后，用建立的模型对工业数据进行仿真预测，最后针对在线过程中检测到的离群点引入离群点分类方法。

3.1 航空煤油生产过程介绍

对于大型炼油装置来说，常减压蒸馏的主要装置之一就是常压塔。航空煤油(简称，航煤)是常压塔的主要馏分，其中一个重要衡量质量的指标是其干点，经济效益直接受干点影响。

本文选用的是某炼化公司航空煤油干点数据，该数据是通过DCS采集与干点相关的现场数据生成。采集频率10 min/次，化验数据采样6次/d，时间间隔为4 h。共采集样本数据近250组用于仿真研究，其中100组作为训练数据，150组作为检验数据，其中150组数据中后50组是代表了过程变化。

本文建模之前，了解现场工艺情况及向相关工艺人员咨询后，确定其中9个过程变量为该模型的辅助变量，首先采用主元分析法，设定贡献率为90%，提取了6个主元作为模型的输入。首先我们针对100组训练数据进行离线离群点检测，为了说明我们所引入的支持向量数据描述方法的有效性我们和常规离群点判别方法“3δ”方法进行对比。下图为两者对离群点的检测图像。其中现场采集的数据时所规定的温度为253℃允许误差为±1.5%。仿真图像如图3、4。

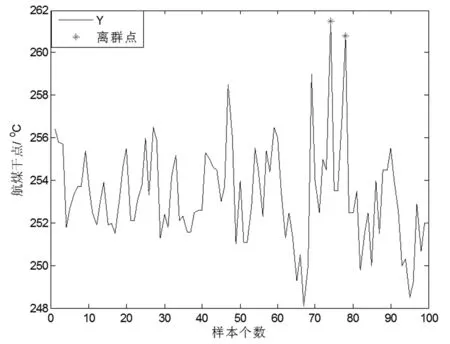
图3 航空煤油干点的3δ离群点检测

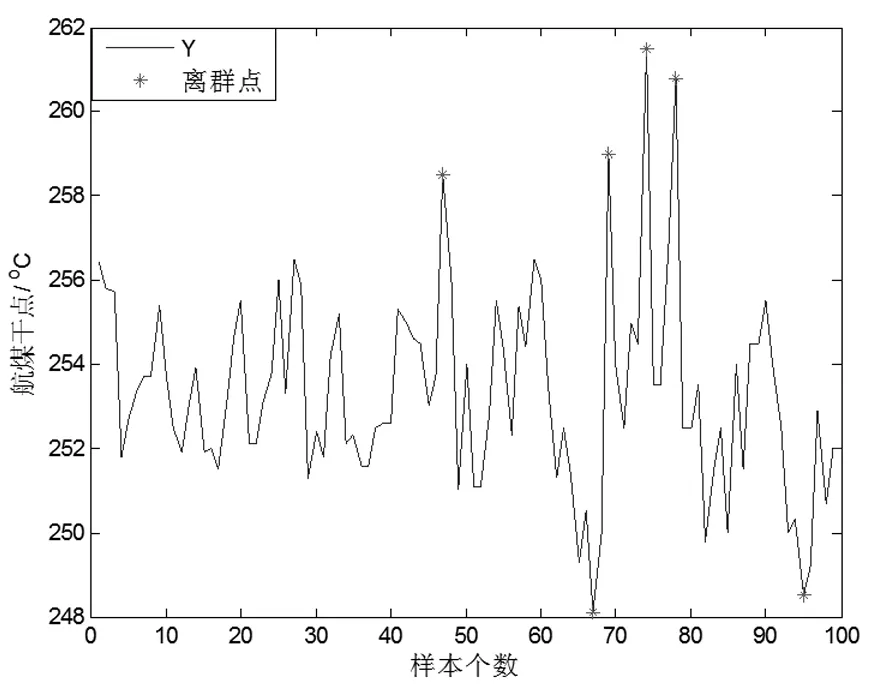
图4 航空煤油干点的SVDD离群点检测

表1是在计算机上的仿真参数，本文以Matlab10.0(a)作为工具，计算机配置为2.82GHz。

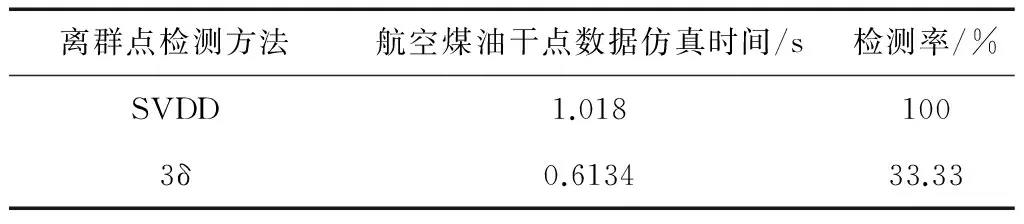
表1 两种离群点检测方法性能对比

由图3、4和表1比较可得，SVDD的离群点检测方法要比 方法检测率要高，也就是说误判率要小，但是SVDD仿真时间比 要长。但是对于离线处理数据而言我们要求高检测率为第一位，因此SVDD可以很好的作为离群点检测的方法。针对离群点检测完的数据采用PLS-RBF建模。仿真如图5。

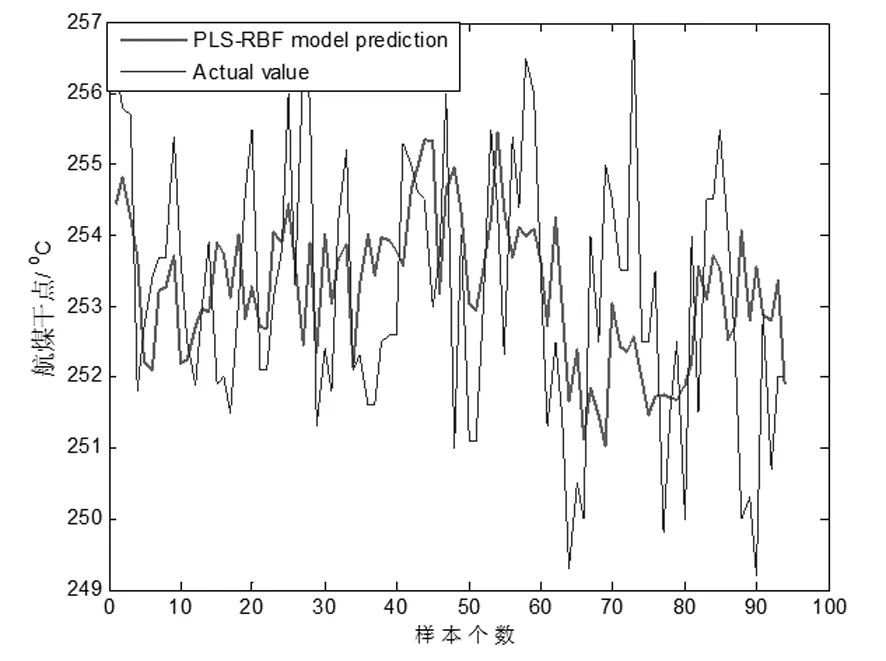
图5 不含离群点的PLS-RBF建模曲线

当模型建好之后在运行过程中，我们要实时的对采集的数据进行预测，有离群点的时候我们也会通过SVDD算法进行检测，但是当化工过程受到物料变化，工艺切换等改变生产流程的影响时，我们所预测到的数据因为偏移了所规定的范围将会被连续的误判为离群点，针对这个问题我们引入的离群点分类的概念就可以轻松的解决这个问题。下面还是以航空煤油干点作为研究的对象，这次我们用100组数据作为训练数据，150组数据作为测试数据，其中150组测试数据中前100组是和训练数据是同一过程的数据，而后50组数据是同一生产装置在改变原料时所确定的数据，以此来表示过程的变化来验证本文所给出出的贝叶斯分类方法的有效性。其中前100组数据时的状态所规定的的标准数值为253℃允许误差为±1.5%，而后50组数据的规定标准值为273℃允许误差为±1.5%，根据先验知识规定在航空煤油干点仿真过程中本文提出的只有1个离群点为脉冲型离群点，短阶跃离群点规定为连续2～10离群点，连续10个以上的离群点为长阶跃离群点也就是新的过程变化，仿真图像如图6、7。

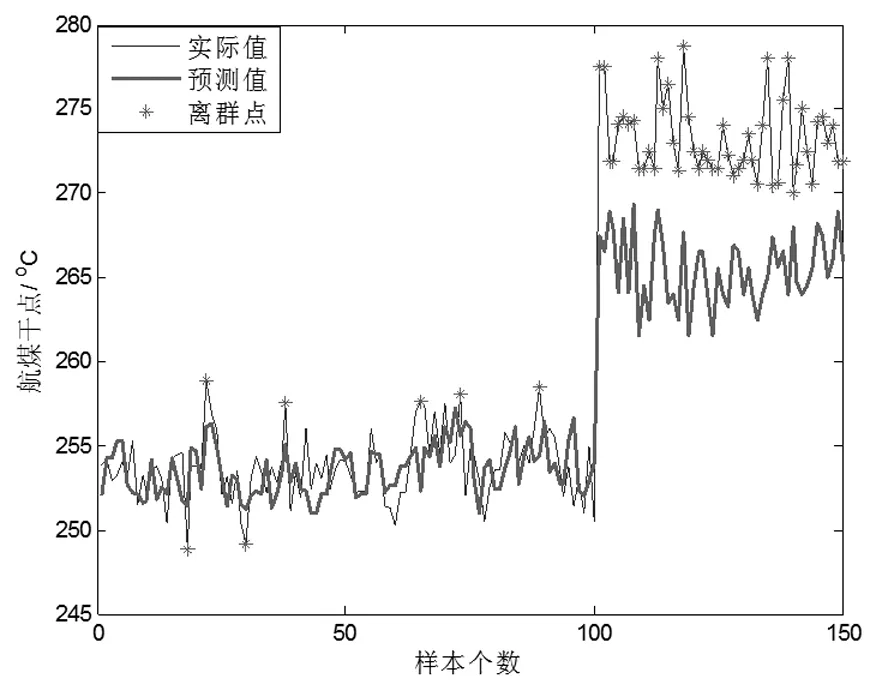
图6 没有参数更新和分类的离群点检测

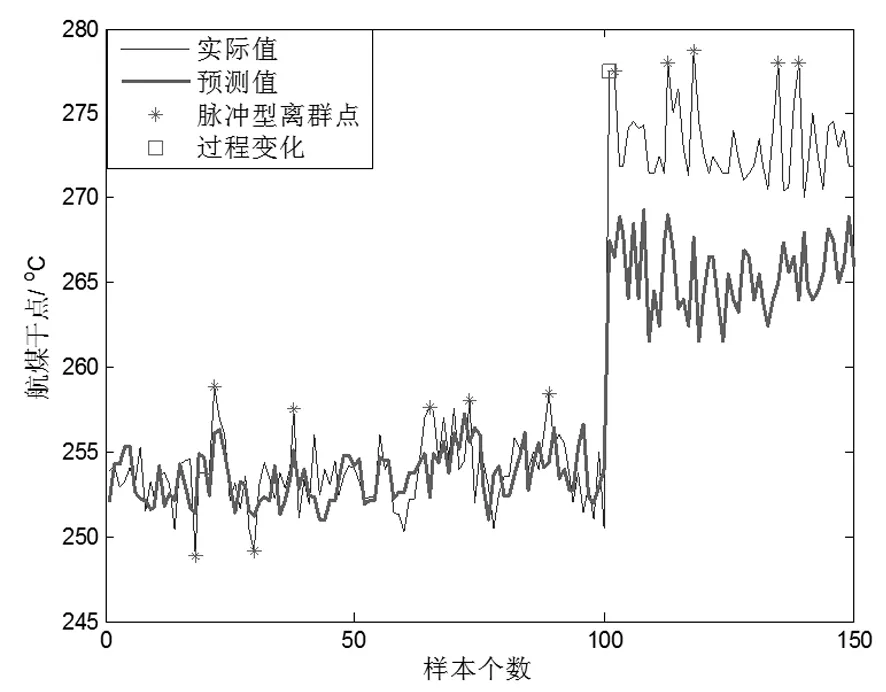
图7 有参数更新和分类的离群点检测

由图6和图7可知，当加入Bayesian分类算法和SVDD参数更新时由过程变化的所引起的数据偏移不会被误判为离群点。由上图也很容易看出，当过程发生变化后模型的预测已经完全不符合实际了，这是由于模型还是原来的模型并没有根据实际数据进行更新，在第四章将会介绍模型更新的相关算法。由于汽油干点过程没有本文所给出出的短阶跃离群点状态，所以在下面的聚丙烯熔融指数的软测量仿真过程中将会体现。

4 结论

本文主要对离群点检测和分类的算法进行了分析和研究。根据故障检测的理论，对在线软测量模型引入了基于支持向量数据描述(SVDD)算法的离群点检测方法。通过仿真研究验证了该方法作为离群点检测算法的有效性。针对实际过程的变化也会引起数据的偏移，导致误判为离群点处理掉问题，本文创造性的引入了离群点分类的概念，将离群点根据实际工况的先验知识主要分为脉冲型、短阶跃型和长阶跃型，其中，脉冲型和短阶跃型是我们要排除的真正意义上的离群点而长阶跃型是代表了化工过程的变化。本文离群点的分类算法采用的是贝叶斯分类算法。通过航空煤油干点数据的仿真研究该方法能有效的判断出离群点的类别，从而实现对离群点的分类。

参考文献

[1]黄光鑫．支持向量数据描述与支持向量机及其应用[D]．成都:电子科技大学，2011.

[2]周开武．贝叶斯方法在化工软测量建模中的应用研究[D]．无锡:江南大学，2009.

[3]刘 敏．臭氧技术中的神经网络软测量建模研究[D].大连:大连理工大学，2003.

[4]Qin S J,McAvoy T J.Non-linear PLS modeling using neural networks.[J] Comput Chem Eng,1992,16:379-391.