基于贝叶斯推断的巨灾债券定价研究

展 凯,丁 冬

(广东外语外贸大学 金融学院,广东 广州 510006)

一、引言

我国是一个巨灾灾害频发的国家,频发的巨灾不单严重影响人们的生活,也会对我国的经济发展造成不利影响。面对巨灾灾害,目前国内的应对方式较为单一,仅限于政府救助和社会捐赠。政府救助对政府财政的依赖性较强,社会捐赠则存在较大的不确定性。长期来看,这两种方式都不具有可持续性。因此,急需其他有效的途径来转移和分散巨灾风险。

20世纪90年代,保险连接证券的出现提供了这样一种转移和分散巨灾风险的有效途径。保险连接证券连接了保险和证券两个市场,通过金融有价证券将保险市场的风险转移到证券市场,极大地分散了风险[1]。在众多保险连接证券产品中,巨灾债券是应用最为成功也是最为广泛的产品之一。其已有的成功发行经验加上我国国内对分散和转移巨灾风险的巨大需求,使得在我国发行巨灾债券具有较大的可行性。

巨灾债券的成功发行离不开对其准确定价,而准确定价的关键又在于对巨灾损失分布能否进行可靠地计量。现有文献多采用损失分布法来对损失频数分布和损失强度分布进行参数估计,由此得出总损失分布模型,但由于巨灾损失“低频高损”的特征,具有鲜明的厚尾性,直接根据历史数据建立的损失分布模型拟合效果并不理想[2]。此外,由于巨灾发生频率低,样本数据少,属于小样本数据,在小样本情况下估计损失分布模型会影响其准确性和有效性。

针对以上两个问题,本文采用贝叶斯推断来估计损失频数分布和损失强度分布。一方面,与直接采用历史数据进行拟合相比,贝叶斯推断通过样本信息对先验分布进行调整,可以得到更符合实际的后验分布。另一方面,贝叶斯推断可以很好地解决小样本情况下数据匮乏的问题[3]。

关于巨灾对象的选择,我们选取广东省台风灾害作为研究对象。我国是世界上受台风影响最严重的国家之一,而广东省又是我国受台风影响最严重的省份。因此,以广东省台风灾害为研究对象具有一定的典型性。

基于此,本文收集广东省1951—2013年间台风登陆次数数据和1983—2013年间的台风损失强度数据,先采用贝叶斯推断方法进行损失频数分布和损失强度分布的拟合,再通过蒙特卡洛模拟方法估计出总损失分布模型,最后运用债券定价公式对广东省台风巨灾债券定价。

二、基本方法

(一)贝叶斯推断

贝叶斯推断的基本方法:将关于未知参数的先验信息和样本信息综合,根据贝叶斯定理得出后验信息,然后再根据后验信息推断出未知参数(见图1)。

图1 贝叶斯推断的基本方法

(二)共轭先验分布

如何确定先验分布是在贝叶斯推断中首要解决的问题。确定先验分布的方法有多种,采用较多的是共轭先验分布。利用共轭先验分布不仅计算方便,而且后验分布的一些参数可以得到很好的解释。

常用的共轭先验分布如表1所示。

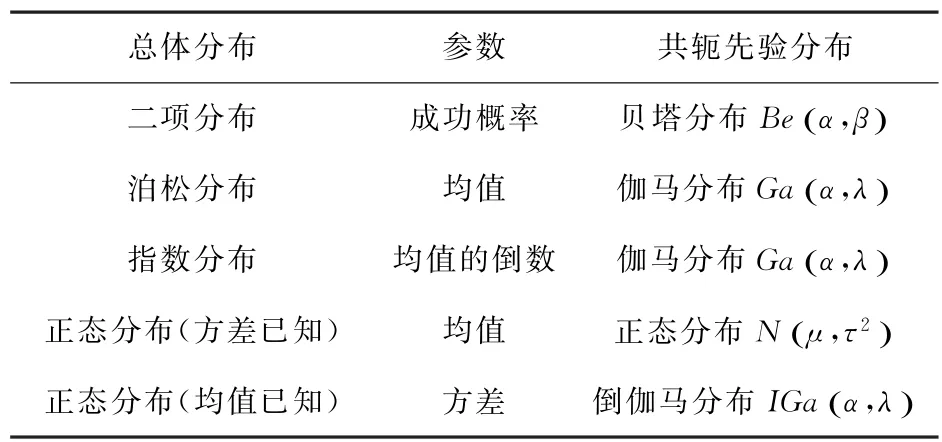
表1 常用共轭先验分布

(三)超参数确定的先验矩法

先验分布中所含的未知参数称为超参数,超参数的确定可以利用先验矩法[4]。

首先根据先验信息得到θ的若干个估计值,记为θ1,θ2,…,θk,一般它们是由历史数据整理加工获得,由此可以计算出先验均值和先验方差,其中:

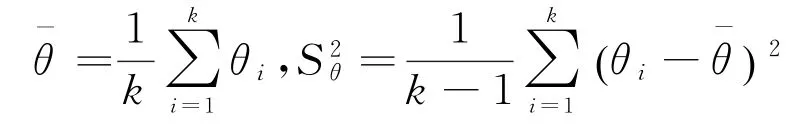
然后令其分别等于先验分布的期望与方差,可得到超参数的估计值。

(四)损失频数的共轭分布

假定损失频数服从Poisson分布,Poisson分布P(λ)均值λ的共轭先验分布为Gamma分布Ga(α,μ)(见表1),取λ的先验分布为Gamma分布[5]。

根据以往历史数据整理加工得出平均每年损失发生频数λ1,λ2,…,λk,利用先验矩法确定先验分布的超参数α,μ。

设x1,x2,…,xn是来自Poisson分布P(λ)的一组样本观测值,据贝叶斯公式可知,后验分布服 从,后 验参数分别为

采用平方损失函数,取后验均值为参数λ的贝叶斯估计,则λ的贝叶斯估计值。

(五)损失强度的共轭分布

假定损失强度服从对数正态分布,即损失强度取对数后服从正态分布N(μ,σ2),当正态分布参数μ,σ2未知时,μ,σ2的联合共轭分布为正态—倒Gamma分布N-IGa,取μ,σ2的先验分布为正态—倒Gamma分布[6]。

根据历史数据整理加工得正态分布均值μ和σ2的估计值分别为μ1,μ2,…,μk和,利用先验矩法确定先验分布的超参数μ0,v0,σ0。

设x1,x2,…,xn(取对数后)是来自正态分布N(μ,σ2)的一组样本观测值,据贝叶斯公式可知,后验分布仍为正态—倒Gamma分布N,后验参数分别为

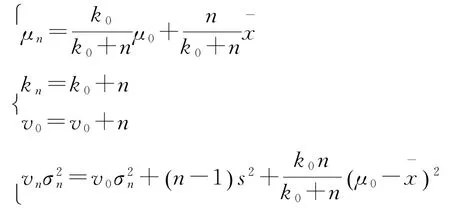
采用平方损失函数,可得到μ的后验均值为μn,σ2的后验均值为。

三、实证分析

(一)数据选取

本文选取1951-2013年间(其中1956与1977这两年没有相关记载)在广东省登陆并造成损失的台风次数作为损失频数的样本数据,在此63年内记载共有109次台风对广东省造成经济损失。选取1983—2013年间登陆广东省的台风对广东省造成的经济损失数据作为损失强度的样本数据,用广东省1983—2013年的CPI定基指数(1983=100)对损失数据进行调整,剔除了直接经济损失低于1亿元的样本数据后,合计共62个样本。

运用贝叶斯方法需要确定先验信息和样本信息。本文将2000年以前(包含2000年)的损失频数和损失强度数据作为先验信息,将2001—2013年的数据作为样本信息。先通过先验信息分别计算出损失频数和损失强度的先验分布,再结合样本信息得出后验分布。

(二)损失频数分布估计

设台风损失频数ξ服从Poisson分布P,ξ的均值,参数λ的共轭先验分布为Gamma分布Gaα(,μ)。

1.Gamma分布Gaα(,μ)中超参数的确定

首先对1951—2000年这50年间(1956、1977年这两年数据缺失)的损失频数进行间隔为5的移动平均,得到参数λ的44个估计值λ1,,进而得到先验均值,先验方差。利用先验矩法,令分别等于Gamma分布的均值和方差,即

将代入,得出

2.Poisson分布P(λ)参数λ的贝叶斯估计

利用2001—2013年这13年的30次损失事件,结合λ先验分布的信息,得到参数λ的后验分 布,其 中t=30,n=13,后验均值为。采用平方损失函数,参数的贝叶斯估计为后验均值,即2.130 5。于是,广东省台风损失频数服从Poisson分布P(2.130 5)。

(三)损失强度分布估计

设台风损失强度服从对数正态分布,即台风损失强度取对数后服从正态分布N(μ,σ2)。正态分布中参数μ,σ2的联合共轭分布为正态—倒Gamma分布。

1.正态—倒Gamma分布N-IGa中超参数的确定

将1983—2000年的34个损失金额(取对数后)作为先验数据,对其进行间隔为5的移动平均,得到正态分布均值μ的30个估计值μ1,,进而得到μ的先验均值,先验方差。类似地,得到σ2的30个估计值,,进一步得到σ2的先验方差。利用先验矩法,令分别等于μ的边际分布的均值和方差，等于σ2的边际分布倒Gamma分布的方差,即

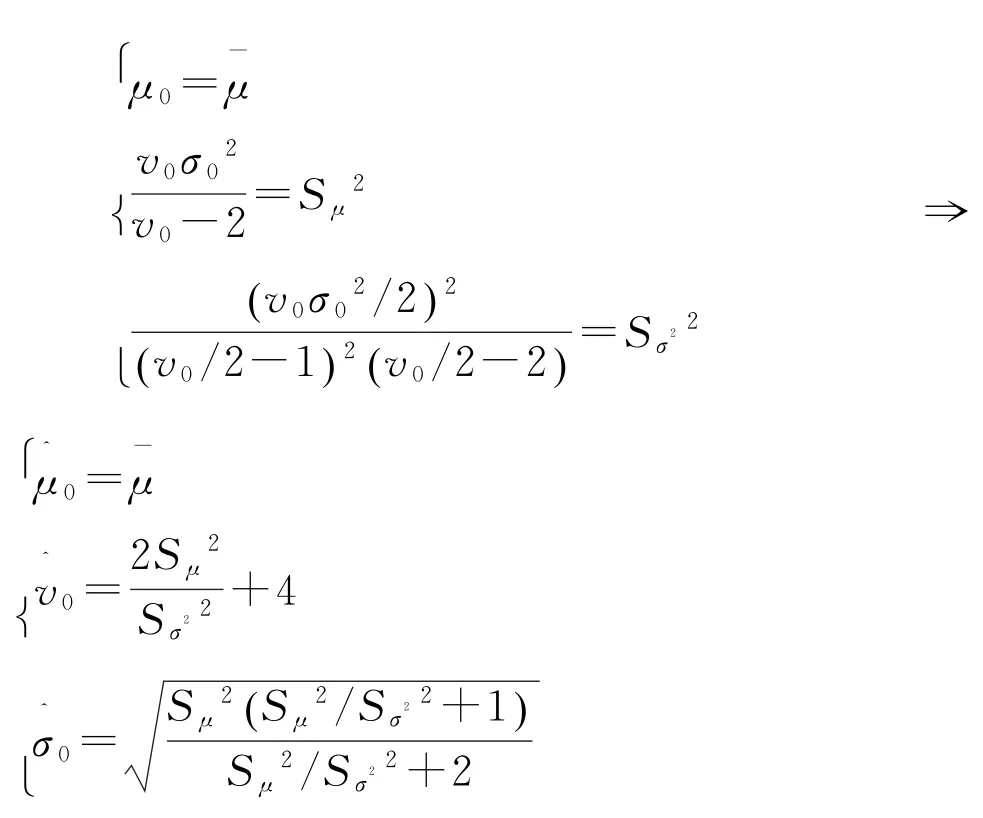
将和代入,得=0.457 1。因此得到正态分布的均值μ和方差σ2的联合先验正态—倒Gamma分布NIGa(2.705 6,5.068 4,0.208 9)。

2.正态分布N(μ,σ2)参数μ,σ2的贝叶斯估计

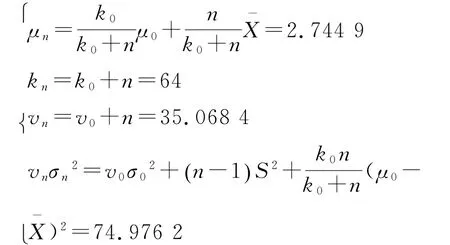
结合2001—2013年这13年30次损失时间,得到后验分布,其中μ的后验均值为μn=2.744 9,σ2的后验均值为,采用平方损失函数,得参数μ,σ2的贝叶斯估计,。于是,广东省台风损失强度服从对数正态分布LN(2.744 9,2.267 3)。

(四)蒙特卡洛模拟法设计

理论上已知损失频数和损失强度的分布,便可求出总损失的复合分布,但一方面采用非寿险精算方法直接计算涉及的卷积公式过于复杂,计算较为困难;另一方面原样本数据较少,直接进行总损失分布模型的拟合会存在较大的误差。因此,基于计算简便性和估计准确性的考虑,我们采用蒙特卡洛模拟法,先扩大样本容量,再对扩容后的样本数据进行拟合,得出较为精确的总损失分布模型。

具体过程如下:首先模拟生成服从损失频数分布的随机数,再根据随机数的值模拟生成与之相匹配的服从损失强度分布的随机数,将所得损失强度的随机数加总便得到总损失的值,重复上述步骤就可以得到每个损失频数随机数下的总损失的值。

本文利用excel软件对损失频数进行一次随机模拟,得到的损失频数为4,然后对损失强度进行4次随机模拟,得到:s1=12.646,s2=21.971,s3=88.689,s4=24.993,将4个损失强度数据相加得到一个总损失S=148.299。

将上述步骤重复1 000次,可以得到1 000个总损失的可能取值。利用这1 000个可能取值,估计出台风灾害的总损失分布情况。

(五)总损失分布模型拟合

通过上述蒙特卡洛模拟法得到1 000个总损失值,为了模型的稳定性,剔除小于1和大于1 000的值,剩余共有876个值,其主要统计量如表2所示。

表2 模拟样本数据的主要统计量

由表2中的统计数据可以知道,样本数据的偏度为2.892 0,属于高度正偏斜;峰度为13.807 0,说明峰的形状比较尖,分布较为陡峭。可以看出,模拟的样本数据符合巨灾风险“低频高损”的特点。

进行总损失分布模型拟合时,需要知道样本数据服从哪种分布。本文选取国内外相关研究使用较多的分布模型和其他典型的分布模型(如Beta分布、Burr分布、Gamma分布、Pareto分布、Logistic分布、Pearson分布、Normal分布、Weibull分布、Log-logistic分布、Lognormal分布、Log-Pearson分布等)作为备选分布,用蒙特卡洛模拟得到的876个样本数据进行拟合,计算出各备选分布的参数值,再用已知参数值的备选分布对样本数据进行拟合优度检验,检验方法为常用的K-S检验、A-D检验和卡方检验。相关的检验统计量越小,说明拟合效果越好。按照统计量的大小从低到高进行升序排序,采用算术平均法计算出各备选分布的平均Rank,平均Rank最小的分布为最优分布[7]。备选分布的拟合优度检验结果如表3所示。

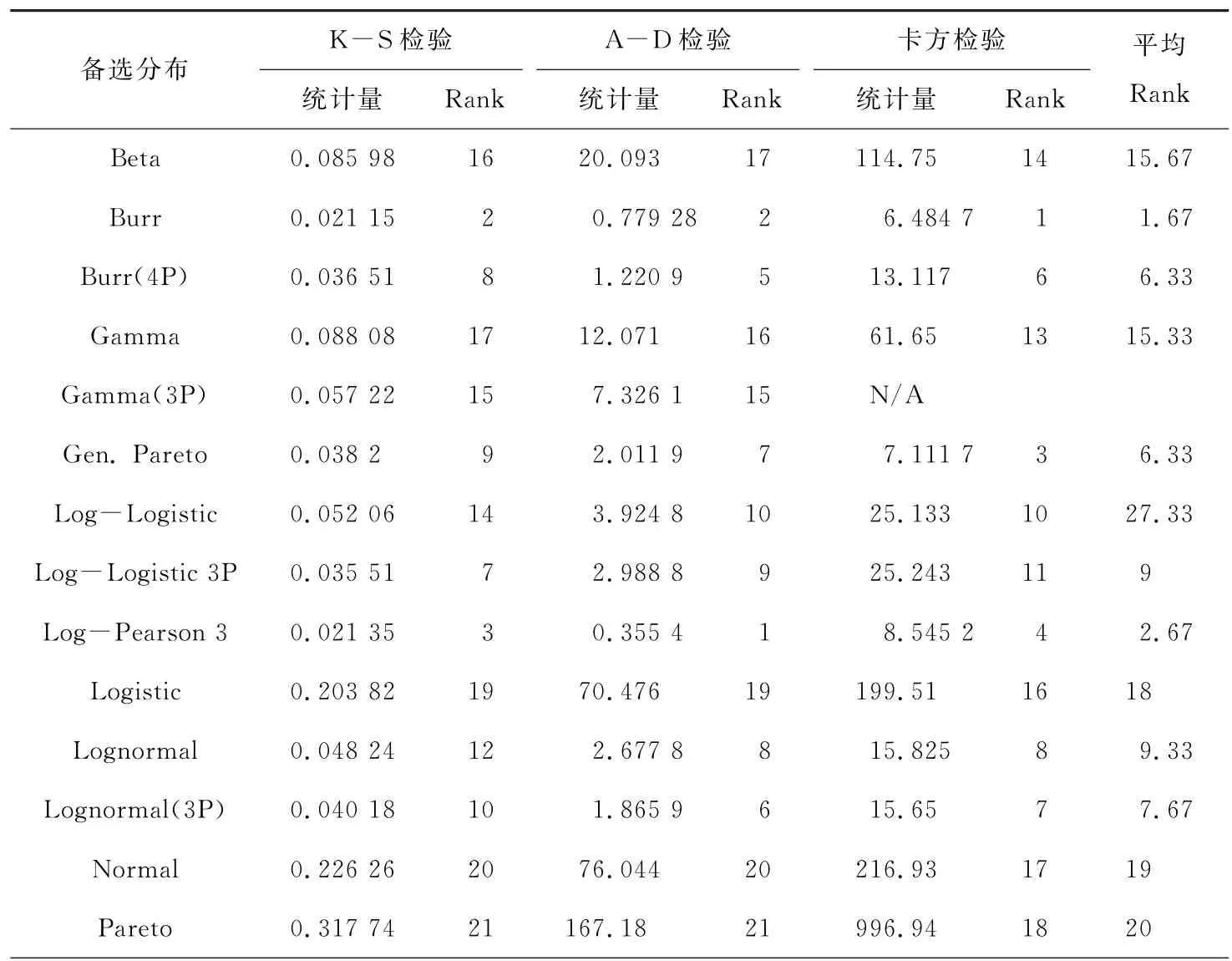
表3 备选分布拟合优度检验结果

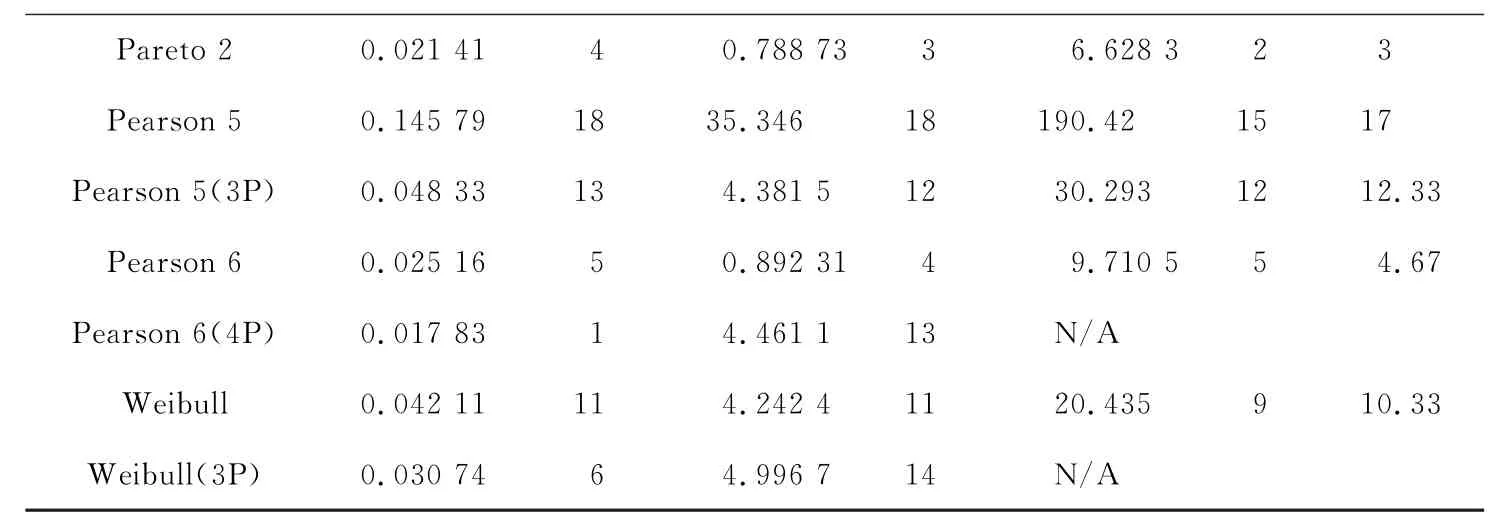
Pareto 2 0.021 41 4 0.788 73 3 6.628 3 2 3 Pearson 5 0.145 79 18 35.346 18 190.42 15 17 Pearson 5(3P) 0.048 33 13 4.381 5 12 30.293 12 12.33 Pearson 6 0.025 16 5 0.892 31 4 9.710 5 5 4.67 Pearson 6(4P) 0.017 83 1 4.461 1 13 N/A Weibull 0.042 11 11 4.242 4 11 20.435 9 10.33 Weibull(3P) 0.030 74 6 4.996 7 14 N/A

由表3我们可以知道,平均Rank最低的是Burr分布,再进一步观察不同置信区间下的拟合情况(见表4),发现在K-S检验、A-D检验和卡方检验下,Burr都能通过检验。因此,Burr分布是备选分布中的最优分布,估计参数为k=3.349 3,α=0.997 09,β=249.68。

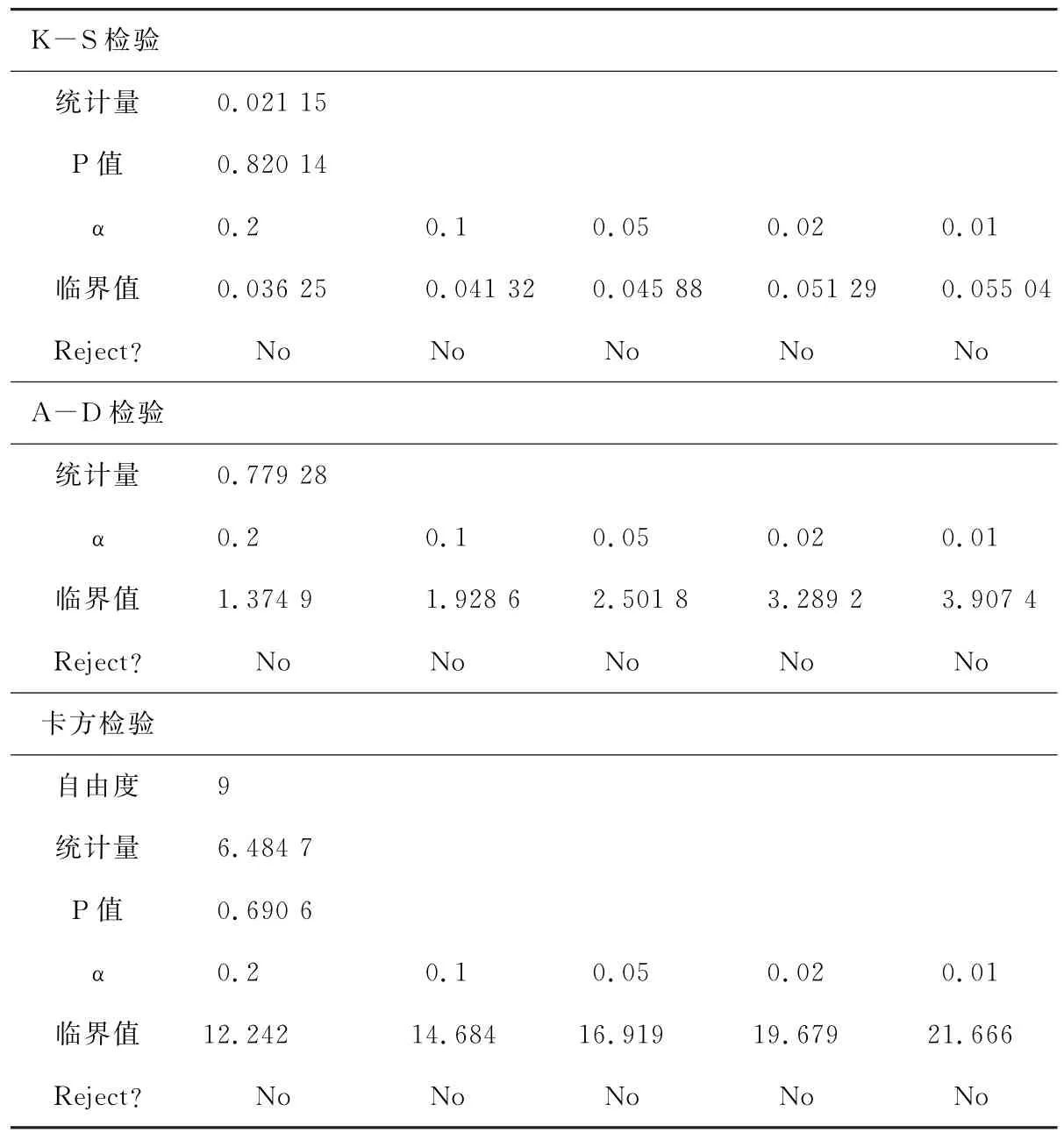
表4 Burr分布具体检验情况

进一步检验Burr分布的拟合准确度,分别画出Burr分布下样本数据的PP图、QQ图、概率差图和概率密度函数图(见图2),可以发现:(1)PP图和QQ图中,样本数据点基本集中在对角线附近;(2)概率差图中,样本数据点在零轴附近上下波动,且波动幅度较小;(3)概率密度函数图中,估计的密度函数与频率图的拟合效果较好。

因此,广东省台风巨灾风险的总损失分布为Burr分布:

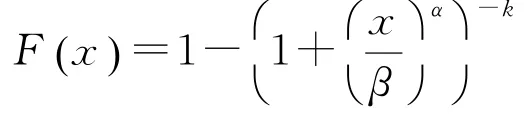
其中k=3.349 3,α=0.997 09,β=249.68。

(六)广东省台风债券的设计

一般债券的构成要素有期限、触发条件、收益率、价格等。巨灾债券作为债券的一种,也应由这些基本要素构成,但考虑到巨灾债券不同于一般的普通债券,巨灾债券有其自身的特点,甚至不同类型的巨灾也需要制定不同内容的条款。因此,下面结合广东省台风灾害的特点,确定各构成要素的具体内容,设计一款广东省台风巨灾债券。

图2 Burr分布图示法检验

首先,期限结构。债券的期限结构一般分为单期和多期,具体选择哪种期限结构需要根据债券的标的来确定。台风灾害具有明显的季节性特征,以广东省为例,广东省台风的多发期为每年的7月至10月,因此,对于台风巨灾债券的期限选用一年期债券较为合适。

其次,触发条件。巨灾的发生会对某一地区造成巨大的损失,因此采用合理的触发条件至关重要。巨灾债券常用的触发机制包括实际损失触发机制、指数触发机制和混合触发机制等。台风灾害损失主要是在一定期间内登陆的台风对某一地区造成的直接经济损失,所以采用实际损失触发机制比较合适。不同的债券类型有不同的触发条件,根据总损失分布计算出触发概率对应的触发值(见表5),选取(154,0.2)、(247,0.1)、(361,0.05)三点分别作为本金保证型债券、本金50%保证型债券和本金全损型债券的触发点[8]。

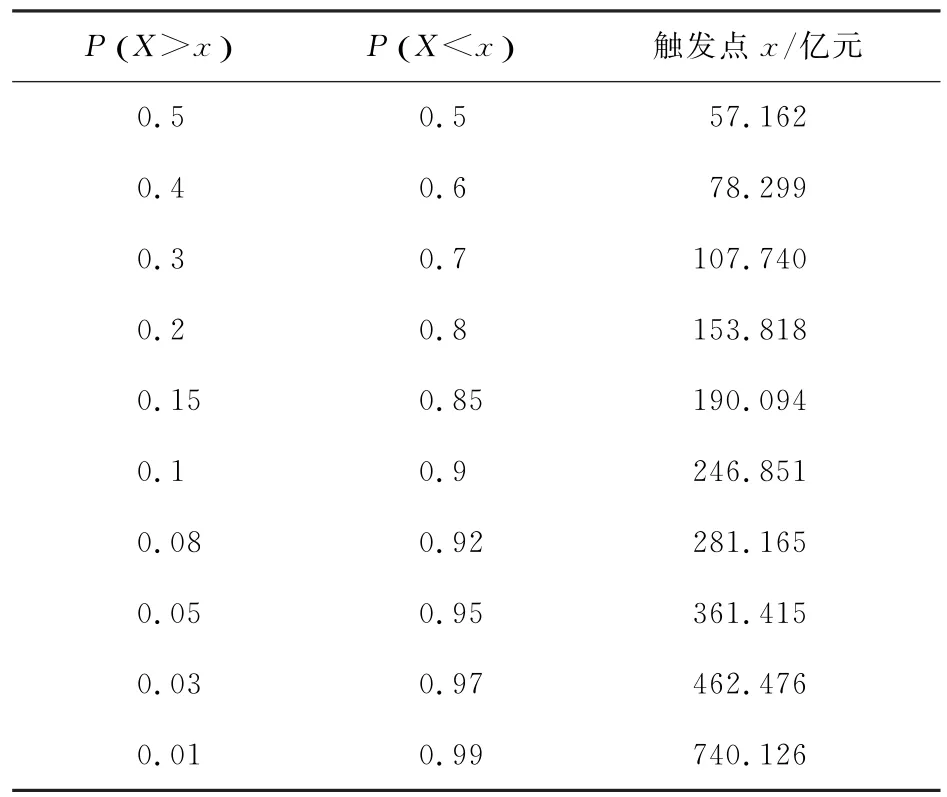
表5 总损失分布触发概率对应的触发点

接着,收益率。巨灾债券作为一种特殊的债券,其触发条件只与巨灾造成的损失大小有关,而与金融市场的波动无关。由于巨灾债券与其他金融产品的相关系数低,导致其市场流动性差,因此与普通债券相比,巨灾债券的投资者会要求高于普通债券的收益率。此外,不同触发条件对应的收益率也有所不同。假定无风险收益率为4%,本金保证型债券、本金50%保证型债券和本金全损型债券的超额收益率分别为0%、4%和8%,总的预期收益率为4%、8%和12%。

最后,债券价格。根据零息债券的一般定价方法,台风巨灾债券的定价公式为:

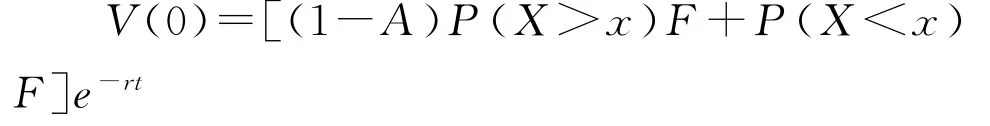
其中,A为触发事件发生时本金损失比率,F为100的债券面额,t为1年,r为预期收益率,P X＞x( )已由前述广东省台风灾害损失概率分布函数确定。

根据上述定价公式,不同类型的台风债券价格如下:

(1)本金保证型债券,票面利率r=4%,触发点为(154,0.2)。

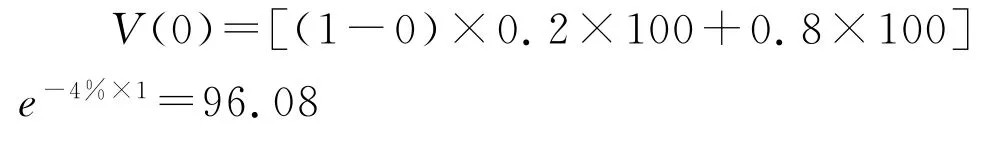
(2)本金50%保证型债券,票面利率r=8%,触发点为(247,0.1)。

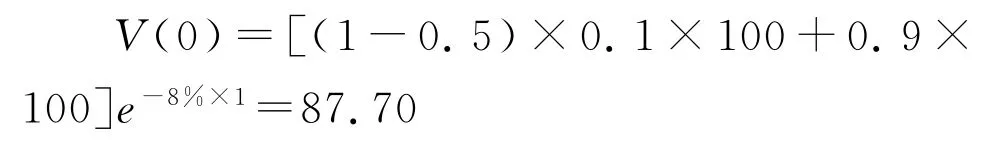
(3)本金全损型债券,票面利率r=12%,触发点为(361,0.05)。

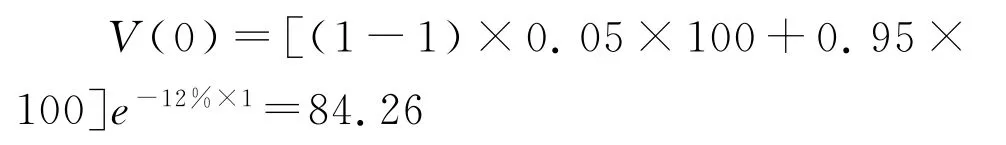
于是,本文选用触发机制为实际损失触发、面值为100元的一年期零息债券来设计广东省台风巨灾债券,具体内容如表6所示。

表6 广东省台风巨灾债券具体条款

以本金50%保证型债券为例:投资者以87.70元购买债券面值为100元、本金保证比例为50%的广东省台风巨灾债券,在一年内,若台风灾害对广东省累计造成的损失达到或超过247亿,则投资者在债券到期时只能获得50元;若累计损失未达到247亿,则投资者在债券到期时可获得100元。

四、结论

本文收集广东省台风灾害数据进行台风巨灾债券实证研究。首先,假定台风损失频数服从泊松分布、损失强度服从对数正态分布,运用贝叶斯推断方法估计出两个分布的参数值。其次,采用蒙特卡洛模拟法扩充样本,对扩充后的样本进行总损失分布模型拟合,发现Burr分布对总损失的拟合效果最好。接着,根据总损失分布选取(154,0.2)、(247,0.1)、(361,0.05)三点作为本金保证型、本金50%保证型和本金全损型三种债券的触发条件,并分别给定4%、8%和12%的预期收益率。最后,按照债券定价公式计算出本金保证型、本金50%保证型和本金全损型三种债券的价格。可以发现:债券价格随着本金损失比例的上升而下降,也就是指债券价格随着本金保障程度的降低而减少,说明收益与风险成正比,与实际情况相符。

贝叶斯推断可以在损失数据有限的情况下,结合先验信息进行统计推断,实现对损失分布参数的有效估计,有效地解决了台风损失数据不足对模型参数估计产生的影响[9]。另外,采用贝叶斯推断进行分布估计还具有可持续性,先得出的后验信息可以在今后作为先验信息,再结合新的样本信息,得到新的后验分布。如此往复,对台风损失分布的估计会不断地改良和深化。

本文的不足之处有:在对先验分布中的超参数进行估计时,只考虑了历史数据和样本数据,没有结合专家经验,这可能会对超参数的估计造成一定的偏差。今后可以加入专家经验进行参数估计,进一步提高参数的稳定性。

[参考文献]

[1]田玲.巨灾风险债券运作模式与定价机理研究[M].武汉:武汉大学出版社,2009.

[2]韦勇凤,李勇,巴曙松.基于贝叶斯推断的巨灾损失数据整合方法与建模[J].中国科学技术大学学报,2013(3):212-216.

[3]卢安文,任玉珑,唐浩阳.基于贝叶斯推断的操作风险度量模型研究[J].系统工程学报,2009(3):286-292.

[4]茆诗松,汤银才.贝叶斯统计(第二版)[M].北京:中国统计出版社,2012.

[5]刘书霞,张新福,米海杰.基于贝叶斯估计的商业银行操作风险计量与管理[J].现代管理科学,2009(4):117-119.

[6]高丽君,杨丰睿.基于贝叶斯推断模型的中国商业银行内部欺诈研究[J].山东财政学院学报,2013(1):12-18.

[7]展凯,林石楷,黄伟群.农业巨灾风险债券化——基于POT模型的实证分析[J].南方金融,2016(5):85-94.

[8]施建祥,邬云玲.我国巨灾保险风险证券化研究——台风灾害债权的设计[J].金融研究,2006(5):103-112.

[9]陈倩.小样本条件下操作风险度量中的参数估计研究[J].北京理工大学学报(社会科学版),2015(3):92-99.