多塔矮塔斜拉桥结构参数敏感性分析

刘榕，伍英，丁延书，罗浩

矮塔斜拉桥是一种介于连续梁桥与斜拉桥之间的桥型，与连续梁相比具有结构新颖、跨越能力大等优点；与斜拉桥相比具有施工方便、主梁刚度大等优点。由于矮塔斜拉桥桥塔矮、梁的刚度较大，对控制塔顶水平位移及梁的变位较为有利，在150～350 m跨径的桥梁中极具竞争性。我国相继修建了芜湖长江大桥(2000年)、福建漳州战备大桥(2001年)、惠青黄河公路大桥(2007年)和大连长山大桥(2014年)等矮塔斜拉桥。韩国、法国、西班牙、巴西、加拿大和美国等国家也都修建了不少矮塔斜拉桥[1-3]。随着矮塔斜拉桥应用的日益广泛，国内外学者对其结构体系、静动力性能、构造方式等方面都进行了相关的研究工作[4-5]。参数敏感性分析在矮塔斜拉桥的桥型选择、设计和施工控制方案等方面都扮演着至关重要的角色，近年来越来越多学者进行了深入研究。樊小林等[5-7]通过建立位移、应力、索力作为的目标函数，分别对施工过程中矮塔斜拉桥的结构参数进行了敏感性分析。刘沐宇等[8]分析了一座四塔矮塔斜拉桥的结构参数敏感性。ZHONG等[9-11]也分别研究了不同结构形式矮塔斜拉桥结构参数的敏感性。目前，对矮塔斜拉桥参数敏感性的研究主要集中于施工阶段荷载作用下的参数敏感性，对使用阶段荷载作用下的参数敏感性研究较少，且衡量敏感系数的标准不明确。本文通过引入无量纲的敏感系数，以一座刚构体系三塔矮塔斜拉桥为工程背景，建立空间有限元模型，选取主梁、主塔、拉索和桥墩的刚度，塔跨比，边跨长度，跨中无索区长度等参数进行结构静动力性能的敏感性分析，得出结构位移、内力和自振特性等对结构参数变化的敏感系数大小，为类似桥梁的设计和施工控制提供参考。

1 结构参数敏感性分析方法

在实际工程结构中，结构参数的实际值与理论计算值之间总是存在一定的误差，导致结构的实际性能与理论值存在出入。为了高效地对结构性能进行把握，只需关注对结构状态影响程度较大的参数。结构参数对结构状态的影响程度体现在结构参数变化引起的结构控制截面的位移和内力变化的幅度。根据各个参数对结构状态影响的敏感程度，将结构参数分为主要结构参数和次要结构参数。敏感性分析不仅可以判断各结构参数的重要性，也为结构优化设计提供了依据[12]。

有限元分析可归结为求解如下平衡方程式：

式中：[K]为总刚矩阵；{δ}为位移列阵；[R]为荷载列阵。

如取设计变量xi为节点位移，将式(1)对设计变量求导，可得：

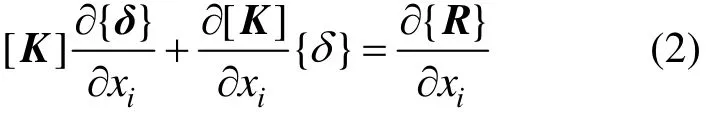
如果式(2)中{R}与xi无关，则：

其中：ix∂∂/}{δ即位移对设计变量的敏感度。同理，可得到应力敏感度的计算公式：

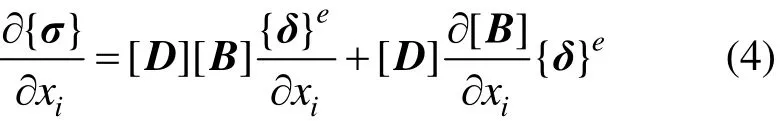
通过有限元计算由式(1)得到位移后，可分别用式(3)和式(4)得到位移和应力对设计变量的敏感性。影响矮塔斜拉桥力学性能的设计变量众多，为了获得某结构参数xi对目标函数的敏感性，可将其余参数固定不变，xi在其可能的范围内摄动，求得目标函数对设计变量xi的梯度值。目标函数对设计变量的梯度可表示为：

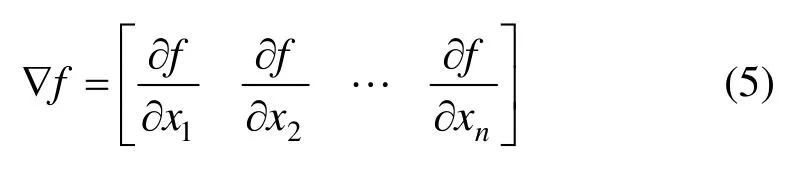
对于设计变量xi，其梯度可用下式近似计算：

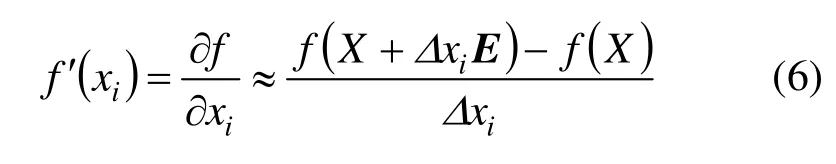
式中：E为单位列向量，在与设计变量xi相应的位置为1，在其他位置为0；Δxi为设计变量的摄动。

值得注意的是，对于非线性结构，参数摄动过大将会损害计算中的局部线性假定而产生过大的计算截断误差；而如果参数摄动过小，过大的计算条件误差将使得计算精度达不到要求。为了衡量各设计变量对目标函数的影响量值，引入如下结构参数的敏感系数：

si为一组无量纲的非负实数，它反映了在基准状态下目标函数对设计变量xi的敏感程度。通过对si中各实数大小的比较，可以对基准状态下各结构参数的敏感性进行评价。

对于矮塔斜拉桥而言，对结构受力影响较大的参数主要有主梁、主塔、拉索和桥墩的刚度，塔跨比，边跨长度，无索区长度等[6-12]，本文通过计算各结构参数的敏感系数评估其对结构性能的敏感性。

2 工程背景及静动力分析

2.1 工程背景

温州瓯江特大桥为三塔四跨预应力混凝土矮塔斜拉桥，采用塔、梁、墩固结-刚构体系。主桥全长710 m，孔径布置为140 m+2×225 m+120 m。主梁采用变高度斜腹板单箱三室断面，顶板宽36.0 m，悬臂长7.0 m。跨中梁高3.8 m，根部梁高6.8 m。主塔为钢筋混凝土结构，中间主塔塔高45 m，两边主塔塔高35 m，塔墩为双肢薄壁结构。斜拉索布置在主梁中央分隔带处，塔根两侧无索区长63 m，140 m边跨无索区长36.5 m，120 m边跨无索区长16.5 m，中跨无索区长18.0 m。

主桥桥型布置图如图1所示，主跨编号从左到右依次为①～④跨，主塔所处位置分别为Z1，Z2和Z3。

图1 桥型布置图Fig. 1 General arrangement of Oujiang bridge

2.2 结构静动力性能及参数分析

采用有限元程序 Midas Civil建立瓯江特大桥主桥有限元模型，全桥一共离散为855个节点，725个单元。主梁、桥墩和桥塔均用空间梁单元模拟，斜拉索用桁架单元模拟。计算模型如图2所示。

图2 有限元计算模型Fig. 2 Finite element calculation model

瓯江大桥成桥阶段各控制截面在不同荷载工况下的位移和内力等计算结果见表1～表4。由于结构基本对称，故表中只列出了一半结构的计算结果。

由表1可以看出，跨中竖向位移受移动荷载影响最大，均匀升温的影响次之；Z1塔顶水平位移受均匀升温影响最大，其次是移动荷载；Z2塔顶水平位移受移动荷载影响最大。

由表2可以看出，对于刚构体系矮塔斜拉桥，均匀升温和梯度升温对结构的作用效应很大，尤其是对主梁边跨和边墩的弯矩。主梁和桥墩在移动荷载作用下的弯矩值也很大，而制动力和支座沉降的作用效应相对较小。

表1 跨中竖向和塔顶水平位移Table 1 Vertical displacement at the middle span and thehorizontal displacement on the top of the tower cm

表3为各工况下拉索索力，为减少篇幅，只列出了边塔Z1左侧和右侧、中塔Z2左侧的最长索和最短索，并依次编号为A～F。

从表3可以看到，移动荷载对索力的作用效应最大；均匀升温对长索的影响大于对短索的影响；梯度温度和支座沉降对索力也有一定影响。由于刚构体系斜拉桥桥墩刚度相对较大，制动力对索力的影响很小。

瓯江桥的前十阶振型如表4所示。

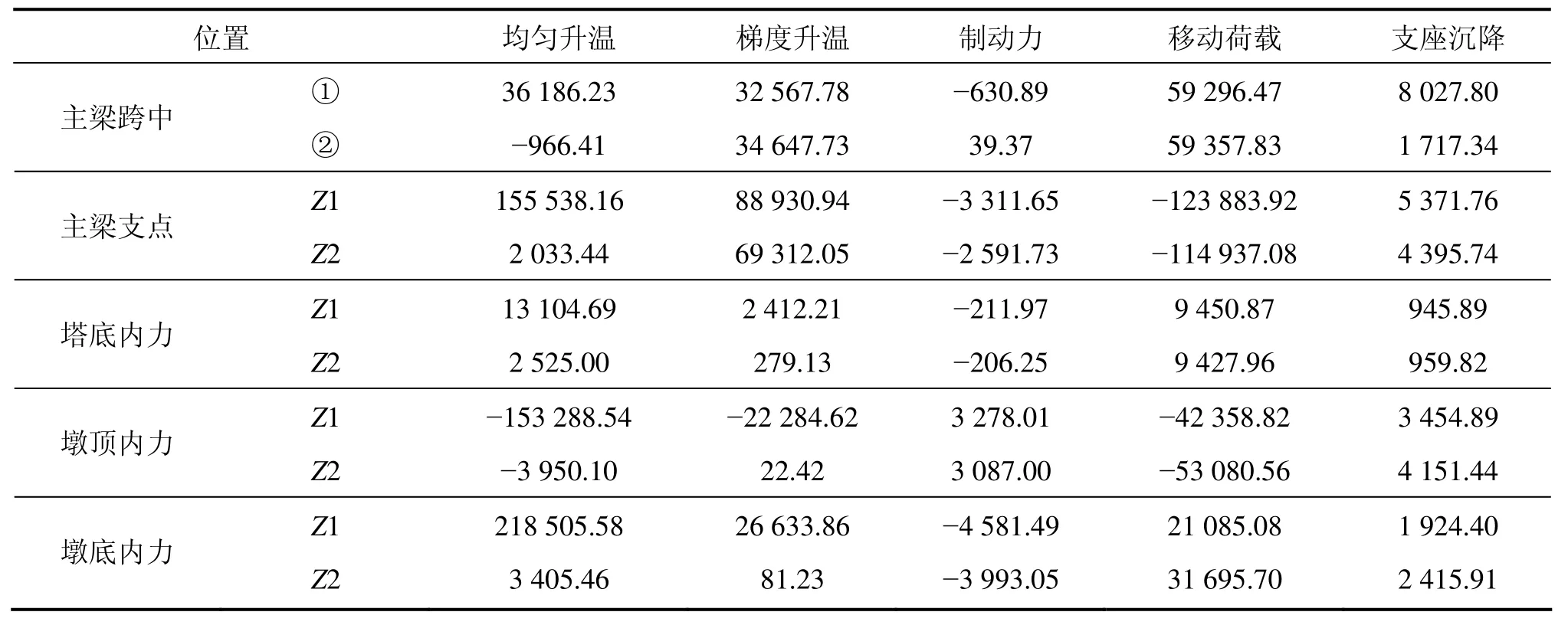
表2 结构内力Table 2 Structural internal force kN·m

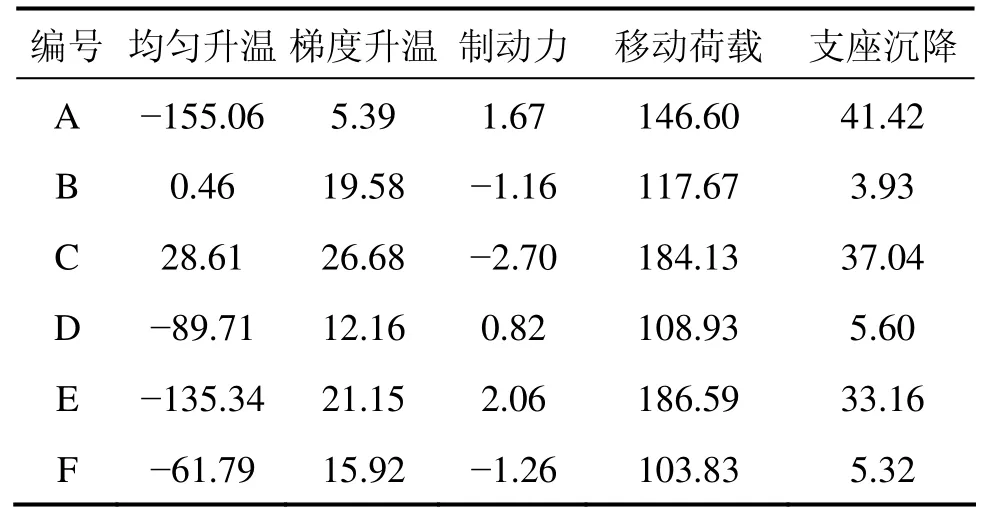
表3 索力Table 3 Cable tension kN

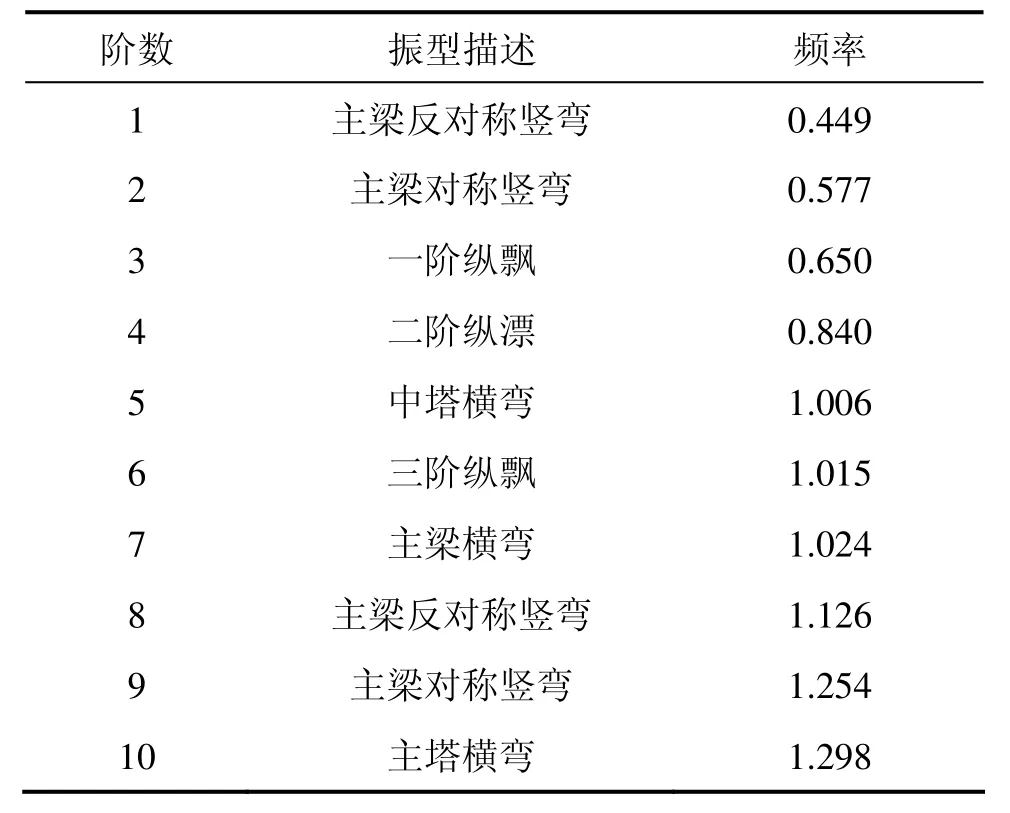
表4 自振频率Table 4 Natural Frequency Hz

可以看到，主梁竖弯频率最低，结构一阶纵漂、中塔横弯、主梁横弯分别在第 3，第 5和第 7阶频率。

3 多塔矮塔斜拉桥结构参数敏感性分析

取摄动大小为 1%，根据式(7)分别计算主梁刚度，主塔刚度，拉索刚度等参数对位移、内力和频率的敏感系数。

3.1 位移的参数敏感性

结构在荷载作用下的位移大小主要反映体系的刚度，由前文知，移动荷载和均匀升温对位移的影响较大，表5给出了各参数对跨中竖向位移和塔顶水平位移在移动荷载下的敏感系数。

由表5可以看出，边跨竖向位移对边跨长的变化最为敏感，对主梁刚度和桥墩刚度变化的敏感度次之；主梁刚度的变化对中跨竖向位移影响最大，塔跨比、桥墩刚度、跨中无索区长度、拉索刚度也有一定影响。塔跨比、主梁刚度、桥墩刚度对塔顶水平位移的影响均较大，但 Z1塔顶水平位移对边跨长的敏感程度最高。值得注意的是，主塔刚度对位移的影响相对较小。

3.2 结构内力的参数敏感性

在均匀升温和移动荷载工况下主梁跨中和支点、塔底、墩顶和墩底弯矩的部分参数敏感性系数计算结果如图3所示。在计算塔跨比、边跨长和跨中无索区长度等参数敏感系数时均采用 1.0%的摄动值，分别调整桥塔、边跨和跨中主梁的等截面区域的构件长度。

表5 跨中竖向位移和塔顶水平位移的参数敏感性系数Table 5 Sensitivity coefficients of the vertical displacement at the middle span and the horizontal displacement on the top of the tower

图3 结构内力参数敏感性系数Fig. 3 Sensitivity coefficient of structural internal force

由图3可以看出，主梁刚度和桥墩刚度对结构内力的敏感系数较大；塔跨比、主塔刚度的变化对相应塔底内力影响较大；边跨长的变化则对边跨、边墩顶内力的有较大影响；拉索刚度、跨中无索区长度对结构内力的影响相对较小。

3.3 索力的参数敏感性

分别计算参数变化对各工况下索力的敏感系数，结果表明，各工况下不同拉索的对各结构参数的敏感系数有一定差异，塔跨比、拉索刚度、主梁刚度是影响荷载作用下索力的主要因素。边跨长、桥墩刚度对索力也有一定影响，但边跨长主要对边塔拉索影响较大。主塔刚度、跨中无索区长度的变化对索力影响较小。温度梯度和移动荷载下部分拉索力的参数敏感性系数计算结果见图4。

3.4 结构自振特性的参数敏感性

表6分别给出了主梁竖弯、纵漂、主塔横弯、主梁横弯的一阶自振频率的参数敏感性系数。

表6 自振频率的参数敏感性系数Table 6 Sensitivity coefficients of the natural frequency

图4 索力参数敏感性系数Fig. 4 Sensitivity coefficient of cable force

由表6可以看到，主梁刚度、桥墩刚度和边跨长对主梁振型的影响较大，塔跨比、主塔刚度则对主塔的振型影响较大，拉索刚度和跨中无索区长度对结构自振特性的影响相对较小。这也反映了矮塔斜拉桥以梁和墩为主要受力构件，拉索分担的荷载比例不大的特点。

4 结论

1) 边跨长对边跨竖向刚度、边塔水平刚度、边跨和边墩墩顶内力的敏感度都很高，适当减小边跨长可以有效提高结构刚度，调整结构内力分布；主梁刚度和桥墩刚度对中跨竖向刚度、结构内力的敏感系数均较大；塔跨比和主塔刚度对塔底内力影响较大，但对结构刚度的影响较小；拉索刚度、跨中无索区长度对结构内力的影响相对较小。这些均表明矮塔斜拉桥主要受力构件为主梁，与一般斜拉桥存在较大差异。

2) 塔跨比、拉索刚度、主梁刚度是影响荷载作用下索力的主要因素，因此，在结构设计时需选择合适的上述参数值。边跨长对边塔拉索索力影响较大，主塔刚度、跨中无索区长度的变化对索力的影响较小。

3) 由于矮塔斜拉桥以梁和墩为主要受力构件，拉索分担的荷载比例不大。因此，主梁和桥墩刚度、边跨长度对主梁振型的影响较大；塔跨比、主塔刚度则对主塔的振型有较大影响；拉索刚度和跨中无索区长度对结构自振特性的影响相对较小。

4) 通过本文的方法计算各结构参数的敏感系数，可以定量地了解各参数对结构力学性能的影响程度，为结构设计和施工过程监控提供参考。

参考文献：

[1] 刘旭政, 黄平明, 许汉铮. 独塔斜拉桥参数敏感性分析[J]. 长安大学学报(自然科学版), 2007, 27(6): 63-66.

LIU Xuzheng, HUANG Pingming, XU Hanzheng.Analysis of parameters’ sensitiveness of cable-stayed bridges with single tower[J]. Journal of Chang’an University (Natural Science Edition) 2007, 27(6): 63-66.

[2] Lozano Galant, Paya Zaforteza. Analysis of Eduardo Torroja’s Tempul aqueduct an important precursor of modern cable-stayed bridges, extradosed bridges and prestressed concrete[J]. Engineering structures, 2017(11):955-968.

[3] 张鹏. 嘉绍大桥参数敏感性分析[D]. 成都: 西南交通大学, 2012.

ZHANG Peng. Analysis of parameters sensitivity of Jiashao Bridge[D]. Chengdu: Southwest Jiaotong University, 2012.

[4] Konstantinos Kris Mermigas. Behaviour and design of extradosed bridges[M]. Ajar American Journal of Neuroradiology, 2009, 20(8): 1470-1475.

[5] 樊小林. 预应力混凝土矮塔斜拉桥施工控制与结构参数敏感性分析[D]. 西安: 长安大学, 2014.

FAN Xiaolin. Analysis of prestressed concrete extradosed cable-stayed bridge construction control and structure parameters sensitivity[D]. Xi’an: Chang’an University,2014.

[6] 秦龙. 矮塔斜拉桥参数敏感性分析及拉索损伤研究[D].西安: 长安大学, 2014.

QIN Long. Parameter sensitivity analysis and cable damage research of extradosed cable-stayed bridge[D].Xi’an: Chang’an University, 2014.

[7] 雷忠伟. 矮塔斜拉桥结构参数敏感性分析[D]. 哈尔滨:东北林业大学, 2015.

LEI Zhongwei. Structure parameter sensitivity analysis for an extradosed cable-stayed bridge[D]. Harbin:Northeast Forestry University, 2015.

[8] 刘沐宇, 孙向东, 涂开智, 等. 四塔单索面矮塔斜拉桥结构参数敏感性分析[J]. 华中科技大学学报(城市科学版), 2009, 26(4): 10-14.

LIU Muyu, SUN Xiangdong, TU Kaizhi, et al. Sensitivity analysis for the structural design parameters of four-tower extradosed cable-stayed bridge with single plane[J].Journal of Huazhong University of Science and Technology (Urban Science Edition), 2009, 26(4): 10-14.

[9] ZHONG San, LI Jun, QING Lei, et al. Analysis of parameters’ sensitiveness of long-span hybrid girder cable-stayed bridge[J]. Key Engineering Materials, 2012:517(1): 817-823.

[10] 刘来君, 倪富陶, 张筱雨, 等. 预应力混凝土矮塔斜拉桥参数敏感性分析[J]. 中外公路, 2015, 35(4): 142-144.

LIU Laijun, NI Futao, ZHANG Xiaoyu, et al. Parameter sensitivity analysis of prestressed extradosed cable-stayed bridges[J]. Journal of China & Foreign Highway, 2015,35(4): 142-144.

[11] LIU Jian, WANG Da. Static parameter sensitivity analysis of long-span cable-stayed bridge based on RSM[J]. Journal of Highway and Transportation Research and Development, 2016, 10(1): 64-71.

[12] Nariman N A. Aerodynamic stability parameters optimization and global sensitivity analysis for a cable stayed bridge[J]. Ksce Journal of Civil Engineering, 2017,21(5): 1-6.