高速铁路换乘需求统计算法研究

李丽辉 ，朱建生，史峰，单杏花

截至2016年底，中国高铁里程已经达到2.2万km，占全球高铁运营里程的65%以上。高铁为旅客出行提供了便利，2017年春运期间，高铁旅客发送量高达近2亿人次，占铁路旅客总发送量的50%以上。虽然高铁线路的开通和开行方案的制定充分考虑了经济、地域和客流时变性等因素，但仍存在部分旅客的出行需求不能通过直达方式满足的情况。因此，弄清中国高铁旅客换乘情况，每种情况下换乘出行量大小，以及占总出行量的比例，对设计高铁列车开行方案的组织策略具有指导意义，对于编制和评价开行方案，为旅客提供中转换乘咨询服务，对旅客换乘方案优化以及研究节点换乘方式都有重要价值[1-3]。换乘研究广泛存在于城市轨道交通中[4-9]。相对于城市轨道交通，高铁旅客换乘具有换乘路网复杂、出行需求随季节变化的特点。由于换乘数据在数据存储时没有进行标记，无法从客票系统中直接获取，因此本文根据24 h内旅客出行数据，进行换乘需求筛选。首先采用换乘方向算法进行全路网换乘需求统计，由于此算法在较大数据量时性能较差，因此，本文提出一种基于OD最短距离的算法统计换乘需求。

1 问题描述

正常情况下，旅客出行会选择一站直达的方式。但目前的列车开行方案不能满足所有站间都能开通直达旅客列车，或是旅客决定出行时无法买到所需区间票额，这两种情况都使旅客无法通过直达的方式完成出行目的，使其不得不选择换乘的方式。本文旨在通过更高效的换乘算法得到旅客的换乘信息，了解换乘情形，进一步分析旅客换乘的原因，从而解决旅客不能直达的问题。

换乘行为是一种多段出行行为，指乘客同一天为了从起始地A到达目的地B，通过不止一次的乘车行为达到目的。多段出行并不全是换乘行为，可分以下几种情况：

1) 换乘行为。换乘行为是指旅客为了到达最终目的地而采取中转乘车方式的乘车行为，包含同城同站换乘行为以及同城异站换乘行为。例如：长沙南->北京，北京->哈尔滨西属于同城同站换乘行为。长沙南->北京西，北京->哈尔滨西属于同城异站乘车。

2) 往返行为。往返行为是指旅客从出发地前往目的地，然后又从目的地返回出发地的旅行行为。往返行为又包括了直接往返和部分往返行为。直接往返行为是指出发地和最终目的地一致的乘车行为，而部分往返行为指出发地和目的地不一致的行为，如：长沙南->武汉、武汉->广州南，此种乘车属于部分往返出行。

3) 多任务出行。多任务出行是指某些旅客到达中转站所在城市办理业务，随后乘车离开再去其他城市的行为，这种也不能算作换乘需求。如：第 1段行程长沙南到武汉，到达武汉的时间是上午9点，第2段行程下午19点从武汉出发去郑州，中间停留了大量的时间在中转城市。

通过以上3种行为对比，总结换乘行为有如下特点：

1) 方向一致性。指每次乘车过程都朝着远离起始地的方向进行。

2) 里程拼接性。指每段行程最短路径里程都小于最初起始地和最终目的地的最短路径。

3) 时间连续性。指换乘等待时间不超过全部行程时间的设定阈值。

因此换乘需求求解思路可概括为，首先利用实名制信息获得同一天多次乘坐高铁的旅客乘车信息；再根据方向一致性特点，排除往返乘车的情形；然后根据里程拼接性特点，排除部分往返乘车的情形；最后判断时间连续性特点是否满足，最终确定换乘旅客。

2 换乘需求统计算法分析

本文根据高铁换乘问题描述的定义，基于高铁路网的基础数据，以及乘客的乘车行为数据进行分析，用于精确统计高铁路网的乘客换乘需求。其中高铁路网数据应包含高铁路网的路线，站点，站序，所属城市，间距里程等信息。而旅客乘车数据则包含了去除敏感信息之后的旅客乘车行为数据。包含了脱敏转化的乘车人标识，乘车日期，每段行程乘车车次，始发终到时间，乘车起始站以及乘车终到站等相关信息。表1为示例的乘车行为数据。

表1 换乘旅客O-D客流数据示例Table 1 Control mode switch principles

对整个问题进行数学模型转化，整个高铁的路网可以映射为一个完整的图结构，其中各个车站为图的顶点，车站之间的路径为图的边。设高铁换乘网络G=(E,V)，其中V为高铁路网中的高铁站点集合，E为高铁站间连接线集合。对于高铁网络上的任意车次，其运行站点及途经路径隶属于高铁路网中的一个子集 G ′= ( E ′,V ′)。

在高铁的路网中，存在多个车站隶属于同一城市的情况，因此在同城换乘统计的情况下，需要建立城市集合及同城车站字典集合。例如天津西站，天津南站及天津站，属于天津同城车站。定义城市集合为 C ={C1, C2,… ,Cm}，定义有同城车站字典集合Sc= {Sc1,Sc2,… ,Scm}，对于其中任意Sck是对应城市 Ck的所有车站集合，有 Sck={V1,V2,… ,Vn}。

依据以上分析和定义，本文建立全路网换乘人数统计步骤如下。首先建立路网模型，之后对路网中的任一站点的所有车次进行换乘人数计算，然后计算同城所有车站的换乘总和，即为一个城市的换乘需求统计，将所有城市换乘人数求和得到全路网换乘需求。在统计过程中的每一个步骤，详细结果都可以单独保存，最终形成对整个路网的换乘数据的多维存储，用于高铁线路规划，开行方案优化的数据支撑和决策支持。

依据问题分析，高铁换乘客流统计的核心转化为一个对于某站换乘客流的统计。本文首先对直观的换乘方向的算法模型进行探讨，讨论其时间复杂度。之后通过分析换乘特点，提出了一种基于 OD最短距离的算法模型，通过与换乘方向算法模型比较，证明该算法可以有效提升统计效率。

2.1 基于换乘方向的高铁换乘需求统计算法

当高铁站只有一条高铁线通过时，如图1(a)所示，基于换乘方向的高铁换乘需求统计算法是对该站上下行方向分别进行统计。首先针对上行方向，统计该站上行方向所有到达人数 Du和出发人数Ou，再统计该站上行到达和出发的 ID 数量 Su。Ou+ Du- Su即为该站在上行方向的换乘人数。由于基于换乘方向的数据统计直接过滤了返程数据和部分往返数据，因此只需判断等待时间是否小于全部旅程时间的60%，将不符合要求的数据过滤，存储结果。在进行 ID数量的统计时采用散列方式以提升运行效率。之后再对下行方向采用同样的方式进行分析，得出下行换乘人数结果。上下行换乘人数之和即为该站的总换乘人数。

当该站为2条高铁线路交汇站时，如图1(b)中所示，则需要按上述方法分别计算2条铁路的不同方向共12个。

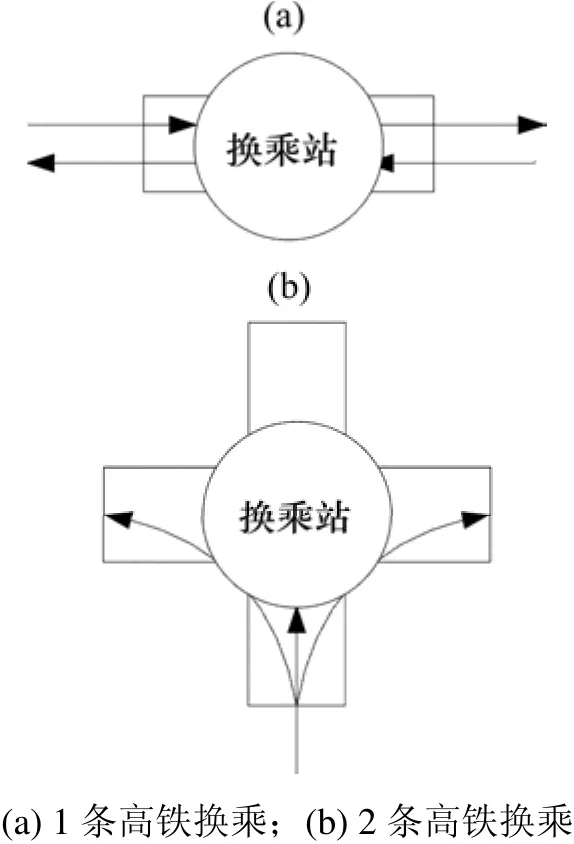
图1 高铁换乘站示意图Fig. 1 Diagram of High-speed transfer station

对该算法进行复杂度分析。设全路网出行总数为N，全路网车站个数为V，对单一车站进行上行到达及出发旅客筛选遍历N次，再进行下行方向分析。假设出行人数均匀分布于所有节点上，则每个站需要筛选 2N/V次，对于交叉站点则需要筛选12N/V。由于交叉节点约占整体路网的 10%左右，由此得到全路网的算法复杂度为

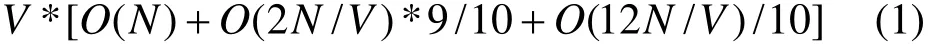
因此全路网的时间复杂度为

最终的算法复杂度约为 O (V * N)。

在实际的应用时，由于高铁乘车数据N的数据量级很大，虽然算法复杂度只是 O (V * N)，但是需要较长的时间，对于单日数据统计达到小时级别，无法满足快速分析响应的需求。

2.2 基于OD最短距离的高铁换乘需求统计算法

根据问题分析中高铁乘客多段出行定义，乘客的出行行为主要包括了换乘行为、返程和部分返程行为及多任务出行行为。则依据换乘行为的定义，进行算法优化。考虑铁路出行成本和旅程距离呈线性关系，因此旅客出行时会尽可能采取最短路径出行。考虑起始地和目的地在路网中的最短距离AB→，以及乘客行车过程中的最短路径AC→和CB→，需满足ABAC＞，ABBC＞且wP≤60%*(P1+ P2)时才属于换乘需求，否则为接续行为，其他则为返程需求和部分返程需求。

那么进行换乘算法优化流程如下：

2) 寻求高铁路网中任意两站间最小出行成本。

3) 依据乘客中转数据判断是否属于换乘出行。

具体的程序流程图如图2所示

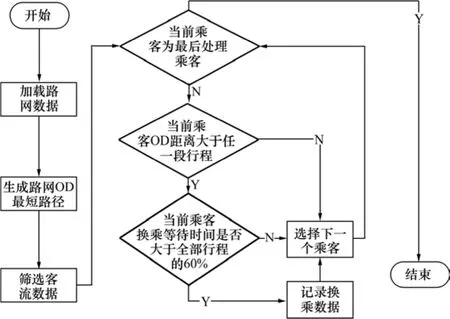
图2 算法流程Fig. 2 Diagram of algorithm flow

2.2.1 建立高铁全路网的图网络模型

对于任意2站之间的边kEE∈有权重W，W为对应的出行成本，在本文中将距离作为出行成本。将高铁线路和车站里程表信息按照线码，里程排序，依照高铁线路设置将高铁站点逐一加入图中的顶点集合；获取线码，线名，车站和里程信息，得到各高铁线路相邻2站里程表，将相邻2站里程作为权重，加入图中的边集合。

2.2.2 寻求高铁路网中任意 2个顶点中最小出行成本

对于寻求全路网中任意两站之间的最小出行成本问题，可以转化为高铁路网模型中的任意两点的最短路径问题。Floyd-Warshall算法是解决全网最短路径的常用算法[10]，简称Floyd算法。在高铁网络和既有铁路网络上计算任意两点之间的最短路，Floyd算法计算复杂度为 3( )^On 。由于路网的节点数较多，为降低复杂度，可以采用分步计算的方法。

（4）共识方面：共识机制从单一向混合方式演进。导致区块链性能降低的重要因素之一是共识算法。PoW、PoS、股份授权证明（DPoS）和拜占庭容错等，各据优势，各有最适用的场景。为提升效率，需在安全性、可靠性、开放性等方面进行取舍，根据场景切换共识机制成了新趋势，并且将从单一的共识机制向多类混合的共识机制演进，运行过程中支持共识机制动态切换，或系统根据当前需要自动选择相符的共识机制。

第1步：在以网络交汇站为节点的简化网络中求解任意两点之间的最短路径。

构建以网络交汇站为节点的简化路网：以交汇站为节点，2个交汇站 u,v若在同一条铁路线上，则连接一条边，两站之间的线路里程为边长为d(u,v)；

采用Floyd-Warshall算法求解简化路网任意两点之间的最短路长，即获得任意2个网络交汇站之间的最短路长p(u,v)。

第2步：对于任意2个高铁站s, t，逐一求解最短路长p(s,t)。

当这2个高铁站s,t都不是网络交汇站时，不妨设 s,t分别在简化网络的边(u1,u2)，(v1,v2)对应的线路段上，d(s,u1)，d(s,u2)，d(v1, t)和d(v2, t)分别为相应线路段的长度，由此可得高铁站s,t之间的最短路长为

当高铁站S是网络交汇站、t不是网络交汇站时，可得最短路长为

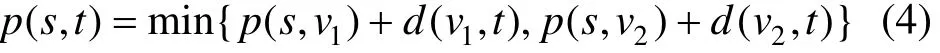
当高铁站S不是网络交汇站、t是网络交汇站时，可得最短路长为

2.2.3 依据旅客换乘数据进行换乘行为判断

得到全路网任意两点的最短路径后，对旅客换乘人数进行统计。依据定义得出换乘需求统计的算法流程如下：

1) 记录同一旅客24 h内所有的出行记录。

2) 根据旅客乘车记录的起始车站和终到车站进行分析，得到中转城市。在分析中转城市时，借助同城车站字典表。

3) 对旅客换乘行为进行判定。定义起始车站到中转车站最短距离为 d1,中转车站到终到车站最短距离为d2，依据最短路径算法执行结果得到起始车站到终到车站的最短距离为d3，当满足d3＞d1并且d3＞d1时，记为旅客换乘。

4) 如果当前乘客满足换乘定义，则对该乘客两次乘车车次的换乘行为人数+1，同时将中转乘车车次放入该中转城市的中转车次集合。

5) 对所有旅客乘车记录执行步骤1～4，得到所有换乘车次人数，以及中转城市与中转车次的集合。

6) 对于每个城市的中转车次的换乘结果进行求和，得出该城市的换乘人数结果。

7) 所有城市的换乘结果求和得到全路网换乘人数。

该算法对所有潜在换乘旅客逐一进行分析，可以得到换乘车次，中转城市，以及全路网不同粒度的换乘数据。

对该算法复杂度进行分析。首先建立路网图结构，其算法复杂度为O(E+V)；优化后的最短路径算法着重分析了交叉站点得到路网最短路径，其算法复杂度为 O (V ^3)/10。最后换乘人数的统计，则变成了对于每个中转行为的依次判断。因此其算法复杂度为对中转行为的遍历，其算法复杂度为O(N)。由于路网图结构和最短路径的结果在路网不变的情况下不会变化，因此只需进行一次构建。之后对于换乘数据的分析都可以依据此前构建和运算结果进行。由此可见基于OD最短距离的换乘需求算法复杂度为O(N)，相对于基于换乘方向的换乘需求算法的复杂度 O (N * V )有了数据量级的提升。

3 算法比较及结果分析

3.1 算法比较

本文基于 2015年全路网基础数据和部分乘车数据作为基础数据，得到换乘结果信息。选择部分车站数据用于2种算法的验证和比较。

3.1.1 算法精度

由于换乘方向算法与人工统计方法思路一致，可假定其得到的换乘数据是准确的。将OD最短距离算法的统计结果与其对比，如图3所示，可知2种算法结果相近，达到 3%以下的相对误差，说明该算法精度较高。

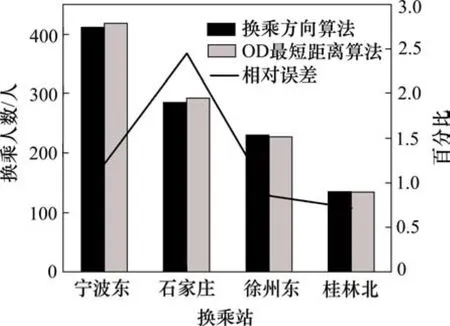
图3 2种算法在部分车站统计结果对比Fig. 3 Diagram of comparison between two algorithm

3.1.2 算法效率

在分析算法复杂度的时候已经指出，基于 OD最短距离的换乘需求统计算法 O(N)的复杂度相对基于换乘方向的算法 O (N * V )的复杂度有了数量级别的提升，则基于样本数据的运行时间比较如图4所示。

从图中可以看出，基于OD最短距离的换乘算法其运行时间大约是换乘方向算法的 1%。由于该算法在实际执行过程中记录了大量数据，因此执行时间较长。但由于全高铁线路具有几百高铁站点，实际运行时间符合算法分析预期。基于OD最短距离的换乘算法在进行全年数据统计时，可以在 4 h内完成。

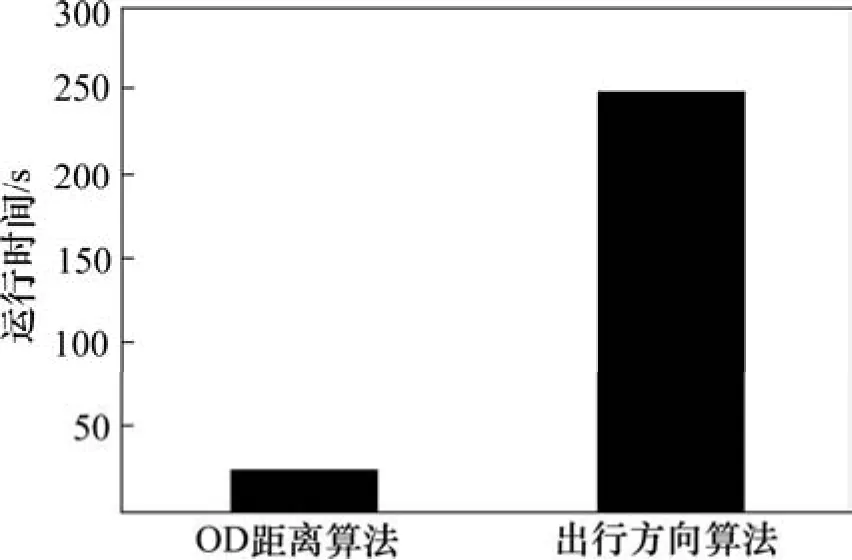
图4 算法运行时间对比Fig. 4 Diagram of comparison between two algorithm running time

3.1.3 算法结果

比较2种算法存储结果，基于换乘方向的算法是针对同城车站进行研究，得出的结果是基于每个城市的换乘人数的总和。基于OD最短距离的换乘算法则记录了具体换乘车次之间的换乘人数，可以作为基础数据做进一步的分析和应用。

3.2 换乘结果分析

3.2.1 换乘人数多的城市

选取某天换乘人数较多的城市，分析OD最短距离算法统计的换乘结果，如图5为所示。发现这些城市都地处交通重镇，并且有多条高铁线交汇。以广州为例，经过广州的高铁线有广珠城际、广深港、京广和南广等多条高铁线，该天的换乘人数高达0.8万人，数据较大，对于分析优化开行方案具有现实意义。

3.2.2 换乘人数多的区间

选择某天换乘人数较多的区间广州南-深圳北-厦门北进行分析，该天换乘人数高达 518人。分析当日换乘的车次组合共有85个，换乘情况如图6所示。

图5 换乘需求大的城市Fig. 5 Diagram of high transfer demand city

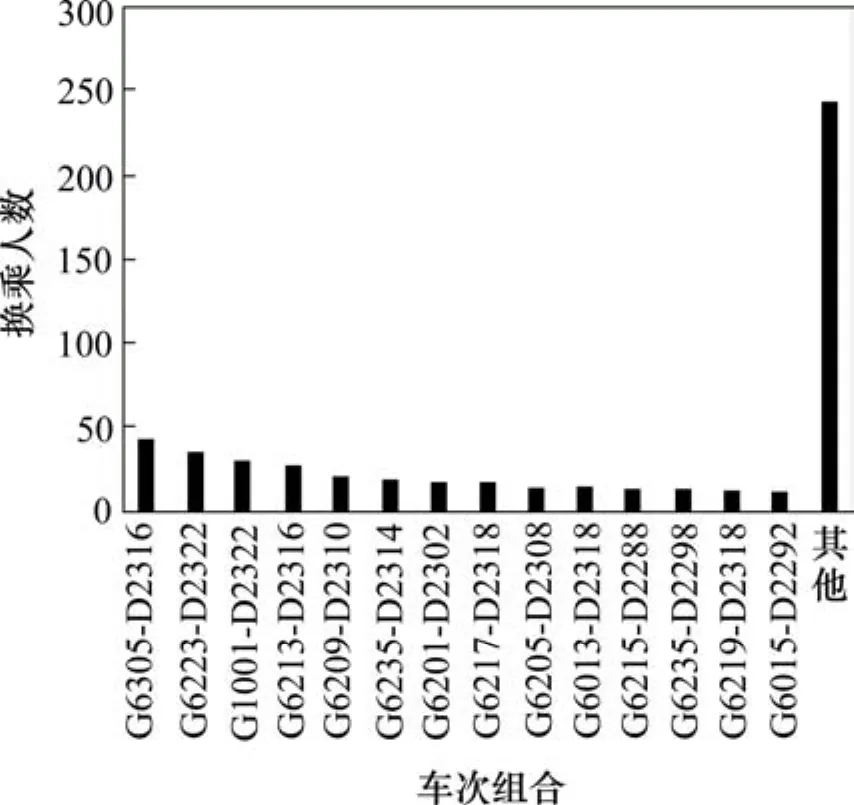
图6 不同车次组合换乘人数Fig. 6 Transfer number of different train combinations

其中换乘人数排在前 3位的车次组合如表 2所示。

表2 换乘人数较多的车次组合Table 2 Train combination of high transfer number

分析上表可知，换乘人数最多的时间是上午，且换乘的整个行程耗时大约5.5 h，换乘等待时间约1 h，此时换乘等待时间占整个行程的20%左右。由于广深线和厦深线车次多、间隔时间短，使广州到厦门的旅客能够方便换乘。

4 结论

1) 分析空间换乘需求，支撑列车开行方案制定以提高运营效率。

2) 分析时间换乘需求，规划列车开行时间来改善出行体验。

3) 分析同城换乘需求，保证同城异站之间换乘的交通接驳。

参考文献：

[1] 史峰, 邓连波. 旅客换乘网络优化设计[J]. 铁道科学与工程学报, 2004, 1(1): 78-82.

SHI Feng, DENG Lianbo. Optimal design of passenger transfer network[J]. Journal of Railway Science and Engineering, 2004, 1(1): 78-82.

[2] ZENG J, YU R R, GUO J, et al. Optimization research of transfer services plan based on heterogeneous demand of railway passengers[C]// Intelligent System Design and Engineering Application. Hainan, 2012: 877-882.

[3] 林冬梅, 刘军. 限制网络上的铁路旅程规划快速求解算法[J]. 铁道学报, 2013, 35(2): 8-13.

LIN Dongmei, LIU Jun. A fast algorithm for railway route planning on restricted network[J]. Journal of the China Railway Society, 2013, 35(2): 8-13.

[4] 刘刚, 李永树. 基于复杂网络理论的铁路换乘系统鲁棒性分析[J]. 计算机应用研究, 2014, 31(10): 2941-2943.

LIU Gang, LI Yongshu. Robustness analysis of railway transfer system based on complex network theory[J].Application Research of Computers, 2014, 31(10):2941-2943.

[5] 禹丹丹, 韩宝明, 董宝田, 等. 基于换乘协同的轨道交通网列车时刻表优化模型[J]. 中国铁道科学, 2015,36(4): 129-135.

YU Dandan, HAN Baoming, DONG Baotian, et al.Optimization model of train timetable for rail transfer network based on transfer synchronization[J]. China Railway Science, 2015, 36(4): 129-135.

[6] SUN X B, ZHANG Y, QIN G Y, et al. Pedestrian transfer time optimization of urban rail transit based on ACP approach[C]// Automation and Logistics. Zhengzhou,2012: 95-100.

[7] 张永生, 姚恩建, 代洪娜. 成网条件下地铁换乘量预测方法研究[J]. 铁道学报, 2013, 35(11): 1-6.

ZHANG Yongsheng, YAO Enjian, DAI Hongna. Transfer volume forecasting method for the metro in networking conditions[J]. Journal of the China Railway Science,2013, 35(11): 1-6.

[8] 李明高, 毛保华, 蒋玉琨, 等. 城市轨道交通网络换乘便捷性研究[J]. 中国铁道科学, 2015, 36(3): 113-118.

LI Minggao, MAO Baohua, JIANG Yukun, et al. Transfer convenience of urban rail transfer network[J]. China Railway Science, 2015, 36(3): 113-118.

[9] XU Y N, YU S J, LIU Y S. Transfer efficiency evaluation between urban metro and buses with grey correlation method[C]// 5th Advanced Forum on Transportation of China, 2009.

[10] Thomas H. Cormen. Introduction to algorithms[M].Boston: The MIT Press, 2002: 629-632.