CRH3型动车组辅助供电系统可靠性分析
2018-05-24赵峰曹茜王开铭
赵峰 ,曹茜,王开铭
高速动车组具有高可靠性,高舒适性,高速性,以及低碳环保等诸多优点,而随着越来越多持有我国自主知识产权的各种国产“和谐号”系列动车组陆续在不同高铁线路上承担重要运输任务,动车组的安全运行始终被高铁运营部门列为首要的工作内容。众所周知,铁路的安全运营问题是生死攸关、涉及人身安全及国民经济的大事,一旦出现故障就可能造成无法挽回的重大事故。动车组电气系统主要由牵引传动系统和辅助供电系统这2个子系统组成,各子系统的可靠性直接影响电气系统及整个动车组的稳定运行。所以,对我国高速铁路上运营的动车组进行相关可靠性分析研究,对于确保我国高速电气化铁路安全可靠运行具有十分重要的意义。国外对列车的可靠性研究起步较早,主要代表有日本、德国及法国[1],已设立了专门的研究机构。我国相关研究始于 2009年,已有学者分别用动态故障树法[2]和贝叶斯网络法[3]等完成了不同型号动车组各子系统的可靠性研究。王华胜等[4-5]首次对动车组进行可靠性研究,完成了CRH2型动车组各子系统可靠性指标分配,并计算了系统百万km可靠度;刘建强等[6]应用最小路集不交化算法,完成了3型动车组辅助供电系统可靠性分析。既有文献未考虑动车组辅助供电系统故障后,工作于降级运行模式下的可靠性,且对系统部件的可维修性及停工相关性[7]考虑不全面。本文拟通过建立CRH3型动车组辅助供电系统的 S-T终端对网络图可靠性模型,根据模型分别用蒙特卡罗-元胞自动机(Monte Carlo Simulation-Cellular Automata, MCS-CA)算法,及其改进算法,即在MCS-CA中融入最小二乘支持向量机(Least Squares-Support Vector Machine, LSSVM)计算,并对比分析系统在不同工作模式下的可靠度与可用度,以期为动车组辅助供电系统的维修、设计提供理论依据。
1 算法简介
1.1 MCS-CA算法原理
网络图可靠性模型近几年开始应用于电力系统、交通系统等可靠性研究中[8-12]。采用CA的传播特性,在 MCS过程中计算系统可靠性,且在离散演化周期内不断地判断系统网络的连通性,这就是利用 MCS-CA算法对网络模型可靠性的评估方法。
MCS是基于区间(0,1)均匀分布产生的随机数进行模拟计算的随机过程,若随机变量Y服从区间(0,1)上的均匀分布,则有随机变量X=F-1(Y),其中Y与X同分布,因此可由随机变量X来代替随机变量Y。
MCS法实质是基于区间(0,1)均匀分布产生的随机数进行模拟计算,产生随机数常用的方法是逆变换法,即,若随机变量Y服从区间(0,1)上的均匀分布,则有随机变量X=F-1(Y),其中Y与X同分布,因此,随机变量Y可以用随机变量X进行替换。
在本文所使用的MCS-CA算法中,CA的工作原理可阐述如下:对于任意网络系统有 G=(V,E),其中,V和E都是集合,分别表示网络中的节点集合和对节点起连接作用的链路(边)集合。此时,网络中的每一个节点可视为1个CA,也就是元胞,每一条链路对应系统中的每一个单元。这里CA为2状态,即激活态或未激活态,它们所对应的状态值可分别为S(j,t)=0与S(j,t)=1。这里每条链路也是2状态,即正常工作状态(对应正常工作概率 pij)或失效状态(对应失效概率 qij),它们所对应的状态值分别为wij=1与wij=0。用CA进行模拟仿真时,只需根据其更新规则来更新每个CA的当前状态,如式(1)所示,也即其及局部转换函数,通过对元胞不停地检测与更新进而来判断系统网络连通与否[13-14]。
MCS-CA算法是将利用蒙特卡罗法模拟产生服从(0,1)均匀分布的随机数ijP′作为CA判断网络连通性的依据。设系统由m个元胞和n条链路组成,共进行N次模拟,在t时刻每个元胞的状态函数为S(j, t), j=1, 2, …, m。每条链路对应的工作概率为pij,通过比较ijP′与pij大小,然后使用CA判断系统网络的连通性。当系统中末端元胞的状态函数值等于 1时表示系统连通,此时系统的状态值为Xc(t),c = 1 ,2,… , N,并记此时的系统结构函数ψ( Xc(t )) = 1,当完成 N次模拟后,统计结构函数ψ( Xc(t ))= 1的次数,记为 M;最后用无偏估计值A˜=M/N计算系统的可用度[15]。
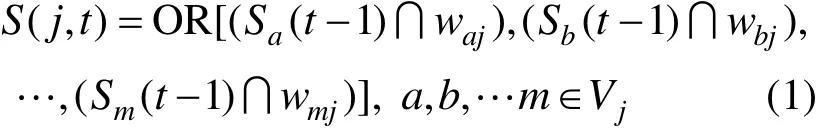
其中: a ,b,… ,m ∈Vj,OR为逻辑或运算,Vj={ j ∈ V , (i,j) ∈ Nn×n,i ≠ j} 。
1.2 LS-SVM分类器原理
设二分类问题的训练集 D={(xi, yi)}, i=1, 2,3, …, n,其中 xi∈ Rd, yi∈ Rd,xi为样本数据,yi为样本,n为样本维数。二分类问题的目标是确定决策函数y(x)=sign(f(x)),分类函数f(x)的表达式如式(2)所示,其中w权重向量,b为偏置项,φ(x)为映射函数[16]。

根据结构最小化原则确定分类函数的参数w和b,可建立如式(3)所示目标函数,其中,C为正规化参数,ξi为松弛变量为二次损失函数。
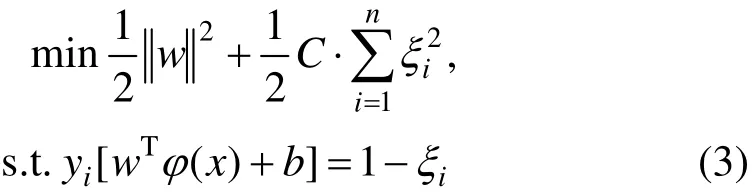
根据目标函数可构造拉格朗日函数如式(4)所示,其中,α=[α1, α2, …, αn]是拉格朗日乘子。
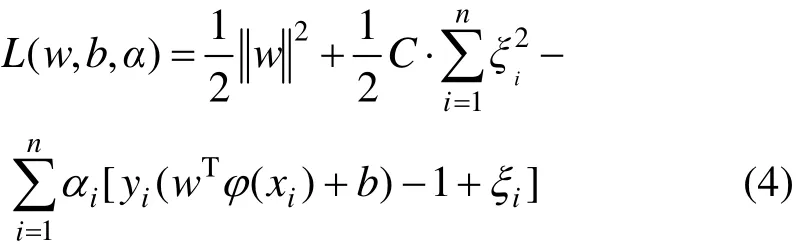
根据KKT优化条件求解式(4),可得:
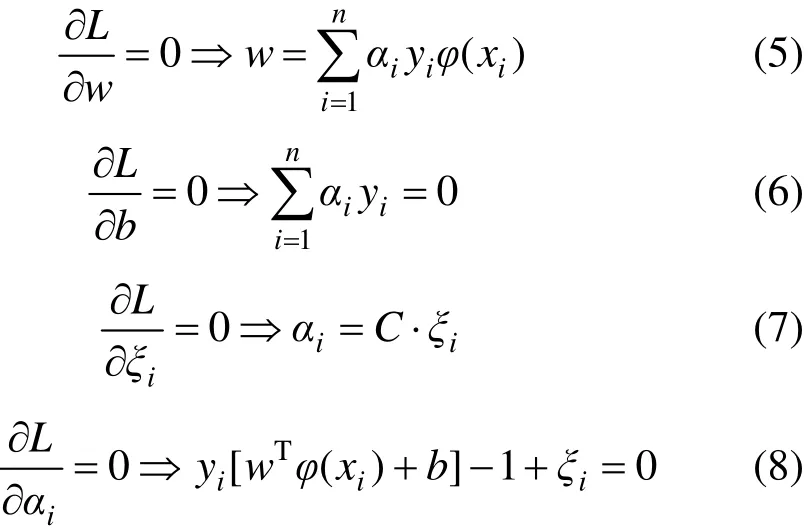
最后可将式(5)~(8)写成线性方程,表达式为:

其中:Ωi,j,α,Y及1v分别为:Ωi,j=yiyjK(xi, xj), i, j=1,2, …, n,K(xi, xj)定义为核函数,它是SVM的核心,本文拟选用径向基核函数(RBF);α=[α1, α2, …,αn]T;Y=[y1, y2, …, yn]T;1v=[1, …, 1]T。
最后通过最小二乘法,可求出参数α与b,并得出如下非线性分类模型:
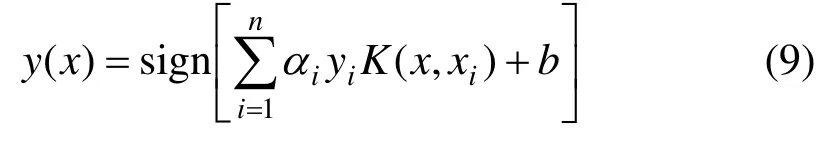
2 系统的可靠性建模及可靠性参数计算
2.1 CRH3型动车组辅助供电系统结构
辅助供电系统从IC03和IC06车中的牵引变流器的中间直流电获取到DC 3 000 V的直流电能,然后在经过辅助变流器单元,变换为三相 AC 440 V/60 Hz交流电作为输出,而车内采用DC 110 V直流供电制式供电。其中,AC 440 V/60 Hz供电母线为充电机供电,而充电机则进一步为蓄电池供电,与此同时,充电机还作为110 V直流母线的电源,向DC 110 V负载供电,其系统结构如图1所示,其中,图示中所对应的各编号说明如表1所示。
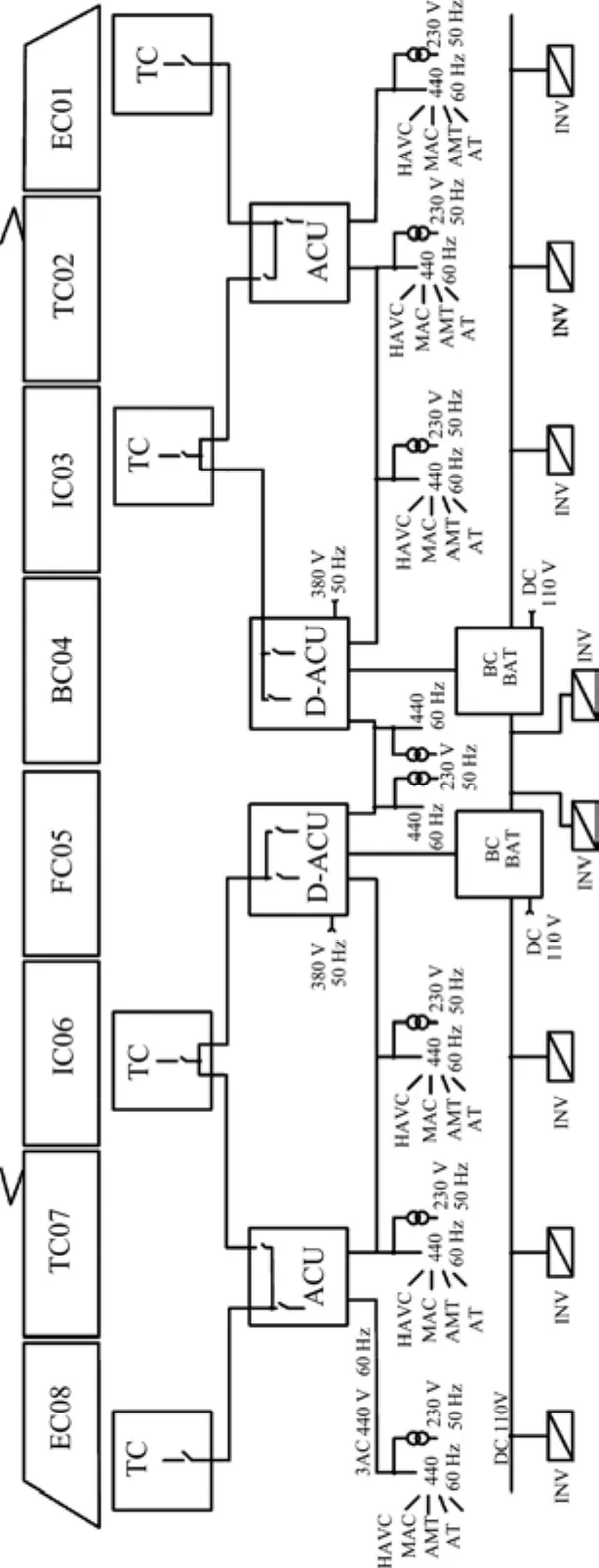
图1 辅助供电系统结构图Fig. 1 Structure diagram of auxiliary power system
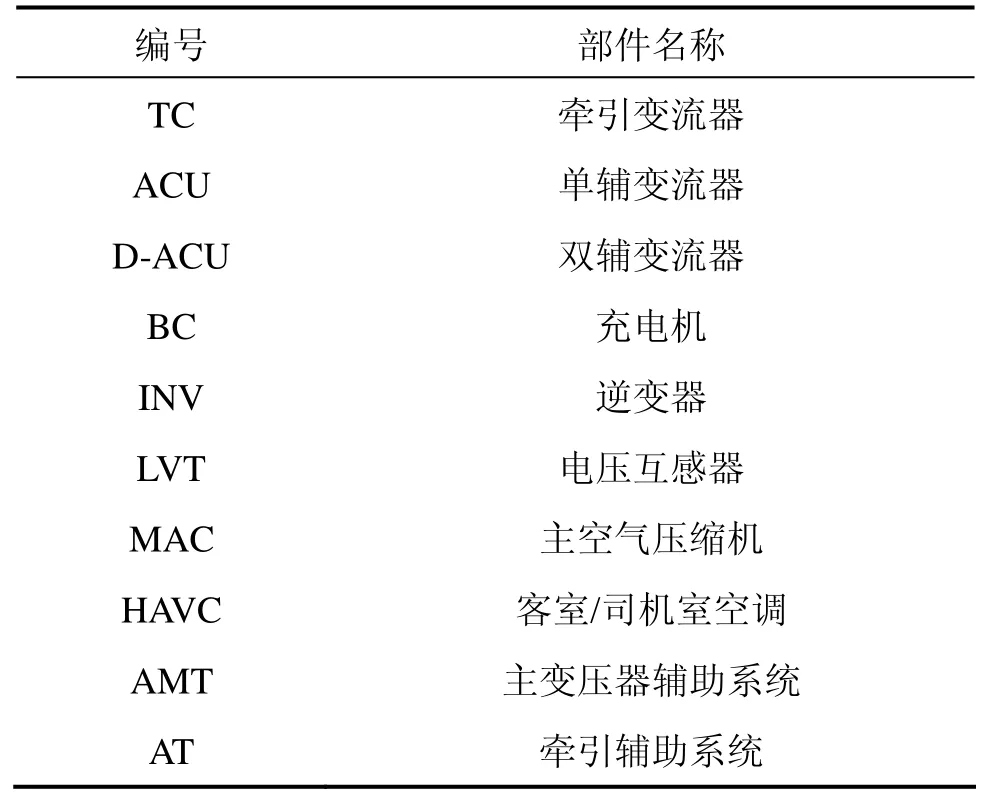
表1 动车组辅助供电系统结构图图示说明Table 1 Illustration of the structure diagram of auxiliary power system
2.2 CRH3型动车组辅助供电系统可靠性模型建立
根据辅助供电系统失效率服从指数分布规律,分别建立了其可靠性框图模型与可靠性网络图模型。
2.2.1 辅助供电系统可靠性框图模型
结合系统结构、工作原理及其部件之间的串、并联逻辑关系分别建立了其可靠性框图模型与可靠性网络图模型。如图 2所示,由不同等效单元(A~Z)组成的可靠性框图模型。
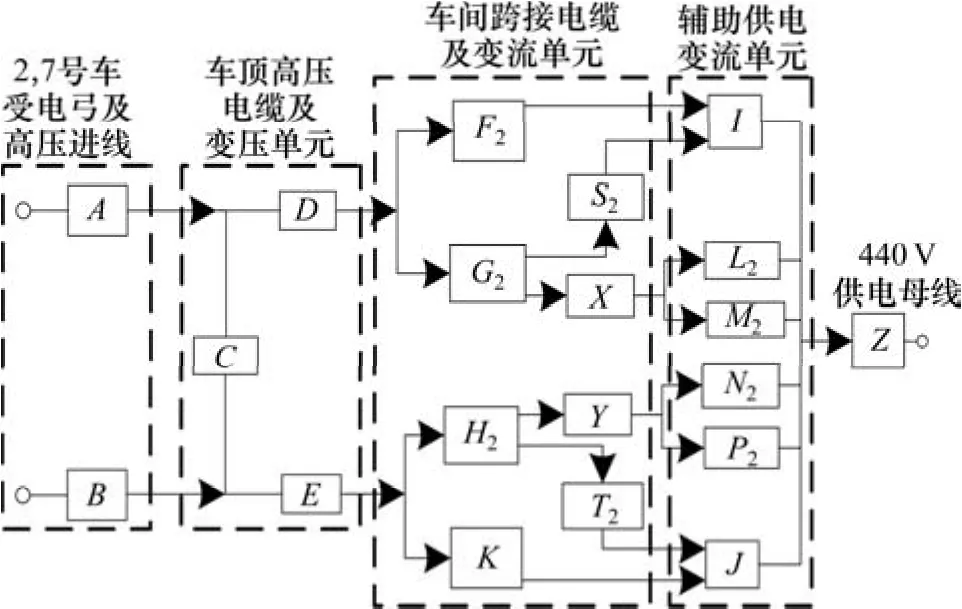
图2 辅助供电系统可靠性框图模型Fig. 2 Reliability block diagram of auxiliary power system
2.2.2 辅助供电系统可靠性网络图模型
动车组操作手册明确规定:当列车处于运行状态时只能升起1个受电弓来获取电能,2个受电弓互为备用系统,故通过等效可将其视为一个单元A1。由于电能可在等效单元C(主要包括车顶高压电缆及跨接电缆)中双向传递,故在网络图模型中,链路C是双向的,而计算系统可靠性时,链路A1由节点S连接至节点2或由S连接至3是等效的。论文中选用链路A1由节点S连接至节点2这一连接方式进行计算分析,网络模型如图3所示。
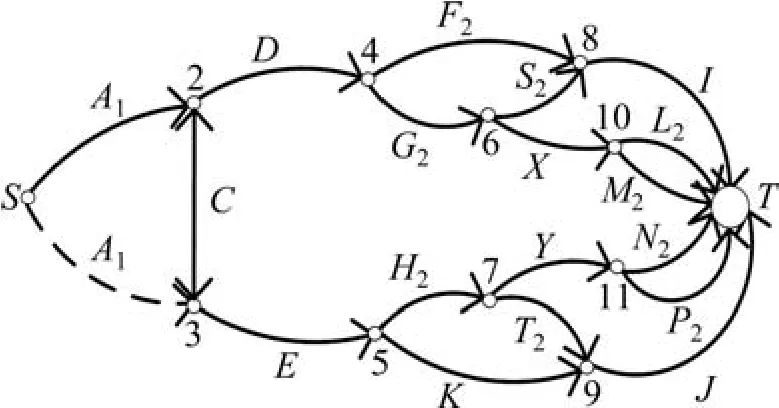
图3 辅助供电系统可靠性网络图模型Fig. 3 Reliability network diagram of auxiliary power system
2.3 辅助供电系统各等效单元可靠性参数计算
1) 串联等效单元可靠性参数计算
n个停工相关的串联部件参数计算公式如下:
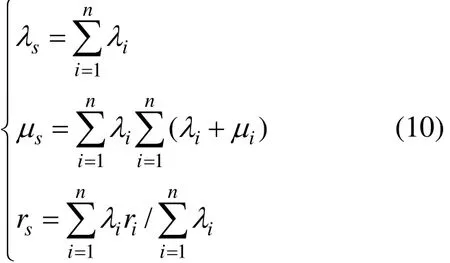
式中:λs,rs和 μs分别为等效单元的故障率、故障维修时间及维修率;λi,ri和μi分别为部件i的相应参数。
2) 并联等效单元的可靠性参数计算
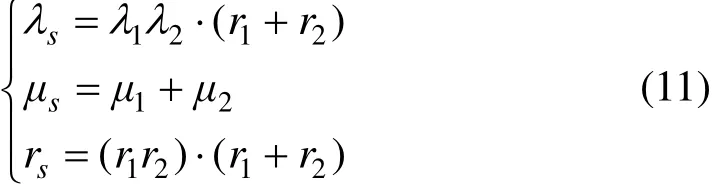
式中:λs,rs和 μs分别为并联单元的故障率、故障维修时间及维修率;λ1,2,r1,2和μ1,2分别为等效单元中部件相应参数。
3) 完全切换储备系统等效单元可靠性参数计算
大多数由复杂系统构成的产品在设计最初,往往采用冗余配置的方式,即在其单元内增设储备部件。完全切换储备等效单元是指当等效单元内的重要部件故障时,备用部件会切换投入运行[17],完全切换储备等效单元的故障率λr、维修率μr、平均维修时间rr的表达式分别为:
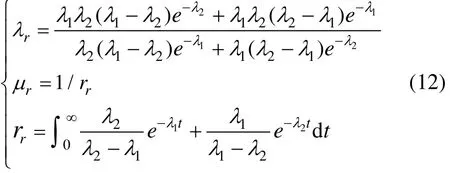
式中:λ1与λ2分别为2个互为储备的部件的故障率。
4) 其他可靠性指标计算公式
平均工作概率PR(1)、瞬时可用度A(t)及可靠度R(t),对应公式分别如下:
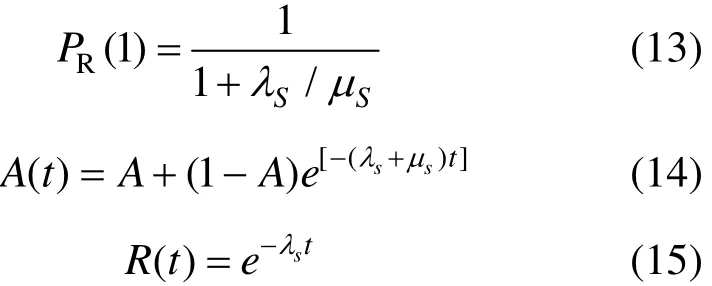
将辅助供电系统各部件可靠性参数代入式(10)~式(12)可得各等效单元的可靠性参数,见表2。
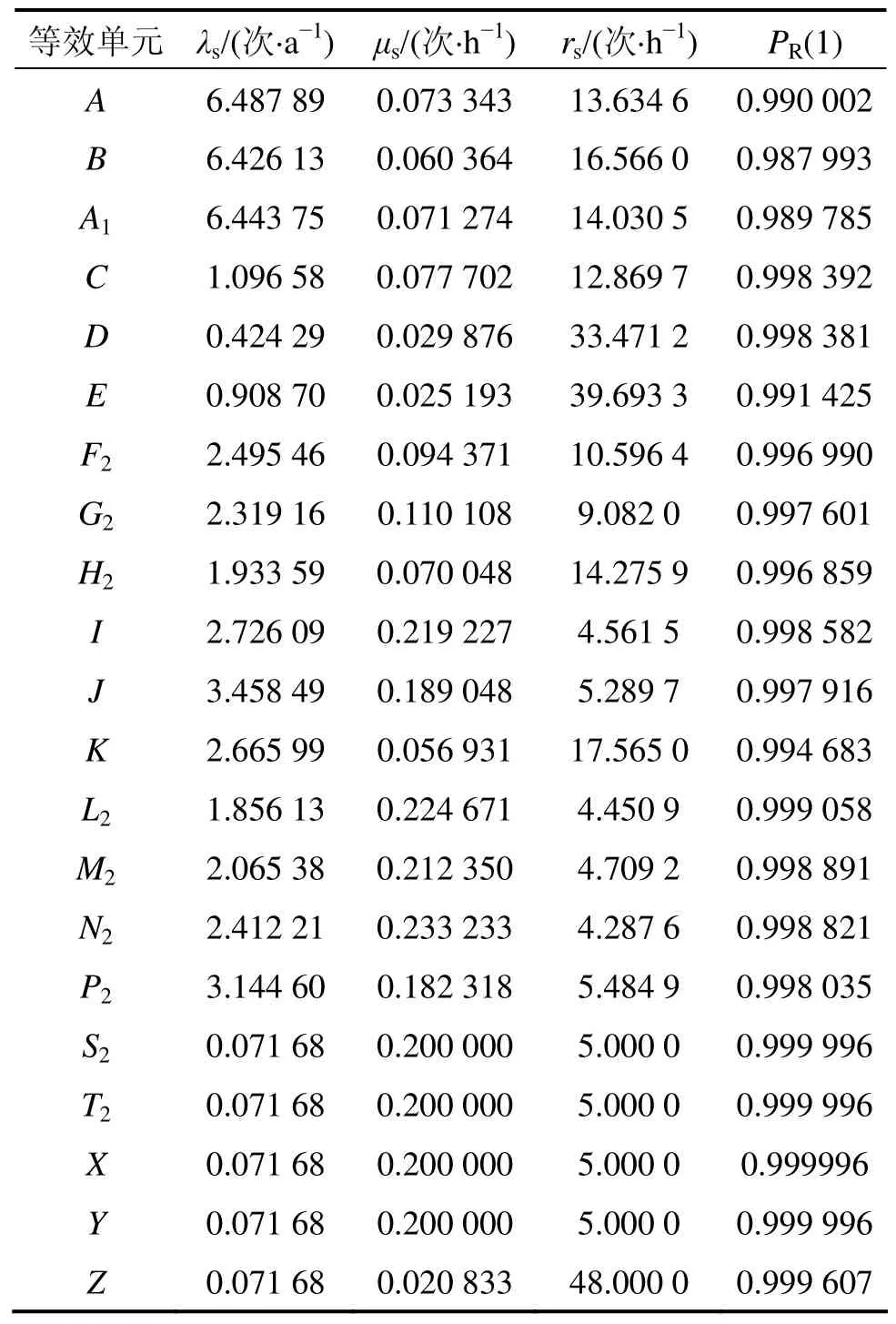
表2 辅助供电系统各等效单元可靠性参数Table 2 Reliability indices of each equivalent unit of auxiliary power system
3 系统可用度及可靠度计算
3.1 可靠性计算的前提假设
1) 动车组电气系统各部件可修,且故障修复后部件或单元可以恢复正常功能。
2) 系统中每一个部件(或等效单元)的工作状态只有失效或正常,即,在系统的可靠性网络模型中每条链路(边)只有2种状态:失效或正常工作。
3)系统中各等效单元之间工作状态相互独立,即存在网络中不同链路(边)之间的状态相互独立。
4) 系统网络图可靠性模型中每个节点完全可靠工作。
3.2 MCS-CA算法计算步骤
基于 MCS-CA算法计算系统可用度的计算步骤中t是元胞CA的离散时刻状态,m是网络图模型中节点的总数,m-1表示用元胞自动机判断网络连通性时最大迭代次数,N表示MCS当前模拟次数,Nmax是MCS总模拟次数。
1) 令 m=17,Nmax=1×105,t=0,N=0,M=0;
2) 设置所有元胞的状态,令S(1,0)=1,S(j,0)=0,其中j=2, …, m;
3) 基于MCS产生一组系统各等效单元的伪随机数ijP ′, i=1,…, m 且 i≠j;
4) t=t+1;
5) 将步骤(3)中产生的ijP′及表2中各等效单元的平均工作概率 PR(1)代入式(1),并对系统所有元胞的状态进行更新;
6) 若 S(m,t)=1表示网络的始端至其中一个终端连通;
7) 若t 8) 若S(j, t)=1,j=10,…, 17代表系统的网络模型处于连通状态,M=M+1; 9) N=N+1; 10) 若N 11) 否则,若N=Nmax则计算系统可用度等同计算网络连通概率即A=M/N。 因为 MCS是一个随机过程,只有当进行模拟次数越多所得结果才能越精确。为保证结果的准确性,论文中用 MCS-CA算法计算时,程序内设定Nmax为1×105,这样虽然可保证结果的准确性,但增加了计算量。所以,为减小计算负担且保持结果的准确性,文中在MCS-CA算法中融入了LS- SVM分类器。 1) 令 m=17,N'max=3500,t=0,N=0,M=0; 2) 用 CA对系统网络模型连通与否进行预分类,生成K组LS-SVM训练数据集; 3) 采用10倍交叉验证法,结合步骤2)中训练数据训练LS-SVM,可得到LS-SVM最优正规化参数C,及RBF参数σ; 4) 利用步骤3)中所得参数C与σ,并结合步骤2)中的训练数据集训练LS-SVM; 本文待分析的数据涉及员工基本信息表、工种表、部门表、出勤表和勤种表五张表。其中主关系表有5000条记录,联系表有44万条记录。系统的开发环境为Visual C++2010,后台数据库为SQL Server 2008。系统主要包括数据导入、数据预处理、系统配置、频繁项集挖掘和关联规则导出五个功能模块。 5) 基于MCS产生一组系统各等效单元的伪随机数ijP ′,i=1,...,m 且 i≠j; 6) 应用训练好的 LS-SVM 的预测模型对步骤5)中的ijP′进行分类,网络连通时归为一类,不连通时归为另一类,当其连通时记M=M+1; 7) N=N+1; 8) 若N 9) 否则,若N=N'max则计算系统可用度等同计算网络连通概率即A=M/N。 本文所有涉及训练LS-SVM时的训练数据集为K=3 000组,其中训练集选择前1 200组,测试集为后1 800组。 TC02/TC07车中各有 1个单辅助变流器(Auxiliary Converter Unit, ACU),即单元I和J,它们分别连接至 EC01/EC08车内的牵引变流器的中间电路。在FC05/BC04车中各有1个双辅助变流器(Double-Auxiliary Converter Unit, D-ACU),均由2个ACU并联组成,即单元L2+M2和单元N2+P2。 动车组辅助供电系统的负载可分为4类,第1类:客室空调系统、通风采暖设备等负载;第2类:主压缩机、各重要设备的冷却系统等负载;第3类:充电机及其他负载;第4类:司机室相关负载。 辅助供电系统正常工作时,6个ACU均投入工作,可保证系统的4类负载全部接入运行。其稳态可靠性指标计算结果见表3。 表3 辅助供电系统正常工作稳态可靠性指标Table 3 Steady state reliability index of auxiliary power system in normal working mode 正常工作模式下基于改进 MCS-CA算法训练LS-SVM的最优参数分别为C1=7.932,σ1=1.460。 将表3相关指标代入式(14)和式(15),所得系统正常工作模式下的可用度及可靠度表达式如下: 表4 辅助供电系统非正常工作稳态可靠性指标Table 4 Steady state reliability index of auxiliary power system in abnormal working mode 3.4.2 辅助供电系统非正常工作模式 1个ACU故障,系统通过冗余操作,增大其余5个ACU的出力,而保证4类负载全部接入运行。 文中考虑了6个ACU依次作为故障单元的情况,情况1:M2故障;情况2:L2故障;情况3:I故障;情况4:N2故障;情况5:P2故障;情况6:J故障。稳态可靠性指标计算结果见表4。 非正常工作模式下基于改进 MCS-CA算法训练 LS-SVM 的最优参数分别为 C2-1=4.835,σ2-1=1.413;C2-2=7.228,σ2-2=1.225;C2-3=5.376,σ2-3=1.006;C2-4=3.611,σ24=1.529;C2-5=4.853,σ2-5=1.056;C2-6=6.594,σ2-6=1.555。 将表4相关指标代入式(14)和式(15),所得系统在非正常工作模式下的可用度及可靠度表达式如下: 3.4.3 辅助供电系统降级运行模式 2个ACU或1个D-ACU出现故障时,辅助供电系统进入降级运行模式,系统只减少第1类负荷,将主要供暖装置及空调系统减少至 1/2的连接输出。 文中考虑了6个ACU中任意2个故障的所有组合情况。分为,情况1:N2+P2故障;情况2:J+P2故障;情况3:N2+J故障;情况4:N2+M2故障;情况5:M2+P2故障;情况6:M2+J故障;情况7:I+P2故障;情况8:N2+I故障;情况9:I+J故障;情况10:M2+I故障;情况11:L2+I故障;情况12:L2+M2故障;情况13:L2+P2故障;情况14:N2+L2故障;情况15:L2+J故障。稳态可靠性指标计算结果见表5。 表5 辅助供电系统降级运行模式稳态可靠性指标Table 5 Steady state reliability index of auxiliary power system in degraded working mode 降级运行模式下基于改进 MCS-CA算法训练LS-SVM的最优参数分别为C3-1=3.774,σ3-1=1.201;C3-2=6.407,σ3-2=1.501;C3-3=6.321,σ3-3=1.309;C3-4=7.622,σ3-4=1.642;C3-5=4.043,σ3-5=1.486;C3-6=8.713,σ3-6=1.374;C3-7=3.695,σ3-7=1.157;C3-8=4.555,σ3-8=1.002;C3-9=6.449,σ3-9=1.441;C3-10=6.001,σ3-10=1.334;C3-11=7.274,σ3-11=1.029;C3-12=7.762,σ3-12=1.383;C3-13=7.203,σ3-13=1.471;C3-14=5.196,σ3-14=1.082;C3-15=5.669,σ3-15=1.408。 将表5相关指标代入式(14)与式(15),所得系统降级运行模式下的可用度及可靠度表达式如下: 对动车组辅助供电系统,分别将其在非正常工作模式与降级运行模式下的不同子情况综合考虑后,得到2种工作模式稳态可靠性指标计算结果见表6。 表6 辅助供电系统2种工作模式稳态可靠性指标Table 6 Steady state reliability index for two kinds of working modes of auxiliary power system 将表6相关指标代入式(14)和式(15),所得系统在2种工作模式下的可用度及可靠度表达式如下: 根据式(16)~式(17),式(60)~式(63),得到辅助供电系统正常工作模式、非正常工作模式和降级运行模式下可靠度及可用度曲线。图4为可靠度对比曲线,图5为可用度对比曲线。 图4 可靠度对比曲线Fig. 4 Contrast of reliability curves 图5 可用度对比曲线Fig. 5 Contrast of availability curves 由图4和图5可知不同工作模式下系统可靠度与可用度大小趋势一致,为正常工作模式<非正常工作模式<降级运行模式。 由表2可知,在3型动车组辅助供电系统中,是ACU变流单元故障率较高,故需对ACU单元增大检修力度。由表4及表5可知,系统在2种故障模式中,若故障单元为I或J,亦或I+J时,其对应系统可靠度低于同等工作模式下其余 ACU或 DACU单元故障的可用度。这是由于单元I和J为独立的 ACU,而其余 4个 ACU,两两并联组成 DACU,当D-ACU中的任意一个ACU故障,可通过另一个ACU继续为D-ACU所在支路提供电能。 1) 基于MCS-CA及其改进算法的计算结果近似相等;融入LS-SVM分类器后,极大地减少了计算所需样本数据及仿真次数,这表明改进算法既提高了计算效率,同时也保证了计算结果的准确性。 2) CRH3型动车组辅助供电系统的6个ACU中,单元 I,J,N2及 P2故障率较高。应加强对这几个单元的检测,以便及时发现故障并抢修。 3) 通过几种工作模式的对比可知,当系统发生故障时,系统单元间的并联连接模式及系统采取不同冗余措施后的不同工作模式(非正常工作模式和降级运行模式),均可有效提高系统可靠性,而保证动车组的稳定运行。 参考文献: [1] 贺帅. 动车组基础制动系统可靠性研究[D]. 太原: 太原科技大学, 2013. HE Shuai. Research on reliability of foundation breaking system for EMU[D]. Taiyuan: Taiyuan University of Science and Technology, 2013. [2] 王健. 基于动态故障树的 CRH2动车组制动系统可靠性分析研究[D]. 北京: 北京交通大学, 2014. WANG Jian. Reliability analysis for CRH2 EMU brake system based on dynamic fault tree[D]. Beijing: Beijing Jiaotong University, 2014. [3] 王衡量, 陆正刚, 张保安. 基于故障树和贝叶斯网络的动车组走行部运用可靠性分析方法[J]. 中国铁道科学,2012, 33(增1): 60-64. WANG Hengliang, LU Zhenggang ZHANG Baoan.Analysis method for operational reliability of EMU running gear based on fault tree and Bayesian network[J].China Railway Science, 2012, 33(Suppl 1): 60-64. [4] 王华胜, 王忆岩, 谢川川, 等. CRH2型动车组可靠性建模与仿真[J]. 铁道学报, 2009, 31(5): 108-112. WANG Huasheng, WANG Yiyan, XIE Chuanchuan, et al.Reliability modeling and assign for CRH2 EMU[J].Journal of the China Railway Society, 2009, 31(5): 108-112. [5] 王华胜. 动车组整车可靠性的验证方法[J]. 中国铁道科学, 2010, 31(3): 82-86. WANG Huasheng. Reliability method of the whole electric multiple unit[J]. China Railway Science, 2010,31(3): 82-86. [6] 刘建强, 郭怀龙, 杜会谦, 等. CRH3型动车组辅助供电系统可靠性研究[J]. 铁道学报, 2015, 37(11): 44-51. LIU Jianqiang, GUO Huailong, DU Huiqian, et al.Research on reliability of auxiliary power system of CRH3 EMU[J]. Journal of the China Railway Society,2015, 37(11):44-51. [7] 赵峰, 梁丽, 王思华. 基于GO-FLOW法的高速铁路接触网系统可靠性分析[J]. 电工技术学报, 2015, 30(12):351-356. ZHAO Feng, LIANG Li, WANG Sihua. A reliability evaluation of high speed railway overhead contact systems based on the GO-FLOW methodology[J].Transactions of China Electrotechnical Society, 2015,30(12): 351-556. [8] Pindoriya N M, Jirutitijaroen P, Srinivasan D, et al.Composite reliability evaluation using monte carlo simulation and least squares support vector classifier[J].IEEE Transactions on Reliability, 2011, 26(4): 2483-2490. [9] 宗刚, 张超, 王华胜. 基于复杂网络理论的高速列车牵引系统部件可靠性研究[J]. 中国铁道科学, 2014, 35(1):94-97. ZONG Gang, ZHANG Chao, WANG Huasheng.Reliability study of the components for the traction system of high speed train based on complex network theory[J]. China Railway Science, 2014, 35(1): 94-97. [10] 宗刚, 张超, 刘文芝. 网络视角下高速列车部件维修关系网络复杂性研究[J]. 中国铁道科学, 2013, 34(3):105-108. ZONG Gang, ZHANG Chao, LIU Wenzhi. Study on complexities in relational network of component maintenance for high-speed train in network perspective[J]. China Railway Science, 2013, 34(3): 105-108. [11] Zio E, Librizzi M, Sansavini G, et al. A combined Monte Carlo and Cellular automata approach to the unreliability analysis of binary network systems[J]. Proceedings of the Institution of Mechanical Engineers Part O Journal of Risk and Reliability, 2008, 222(1): 31-38. [12] Hardy G, Lucet C, Limnios N. K-terminal network reliability measures with binary decision diagrams[J].IEEE Transactions on Reliability, 2007, 56(3): 506-515. [13] Rocco C M, Zio E. Solving advanced network reliability problems by means of cellular automata and Monte Carlo sampling[J]. Reliability Engineering and System Safety,2005, 89(2): 219-226. [14] 阮渊鹏, 何桢. 基于 MCS-CA的考虑共因失效的复杂系统可靠性评估[J]. 系统工程与电子技术, 2013, 35(4):900-904. RUAN Yuanpeng, HE Zhen. Reliability evaluation of complex system with CCF based on MCS-CA[J]. System Engineering and Electronics, 2013, 35(4): 900-904. [15] Yeh Weichang. A MCS-RSM approach for network reliability to minimise the total cost[J]. International Journal of Advanced Manufactuuring Technology, 2002,22(9): 681-688. [16] Johan A, Suykens K, Tony Van Gestel, et al. Least squares support vector machines[M]. Singapore: World Scientific Publishing Co. Pte. Ltd, 2002: 71-111. [17] 郭永基. 可靠性工程原理[M]. 北京: 清华大学出版社,2002: 45-55. GUO Yongji. Principles of reliability engineering[M].Beijing: Tsinghua University Press, 2002: 45-55.3.3 改进MCS-CA算法计算步骤
3.4 辅助供电系统可用度及可靠度计算
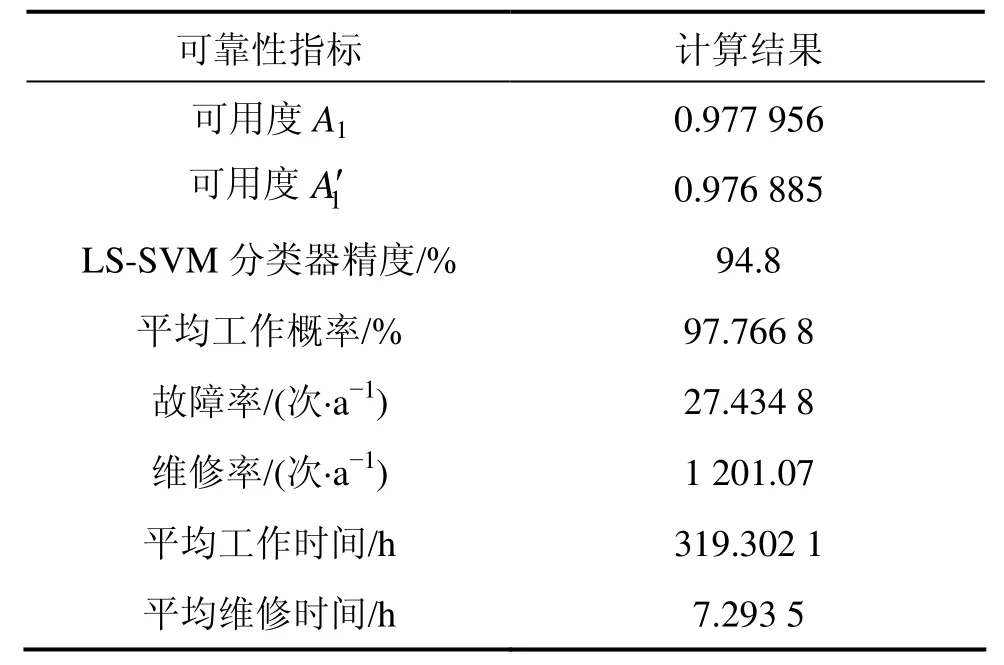

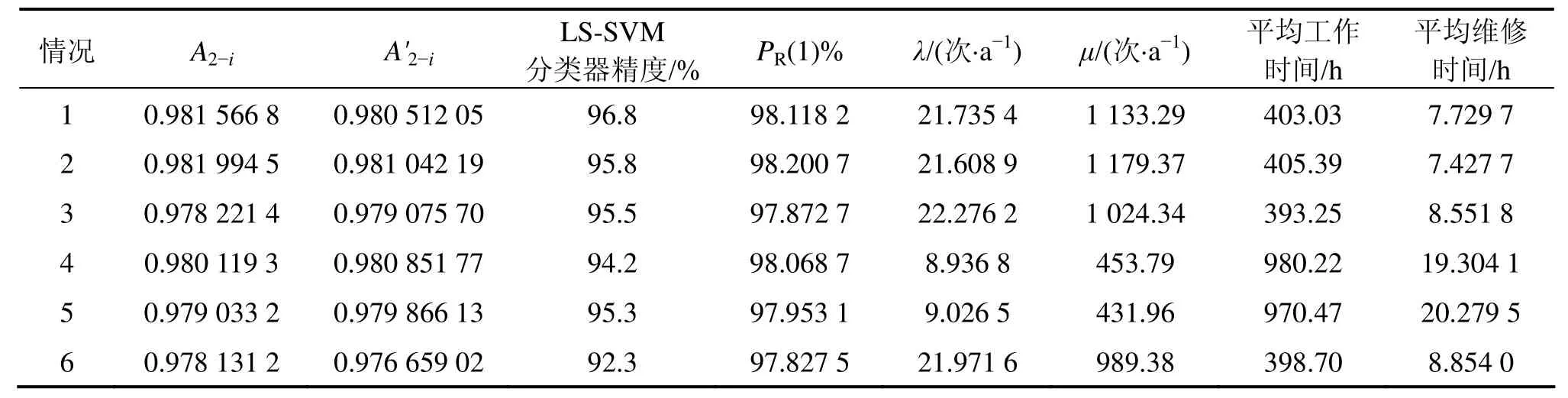
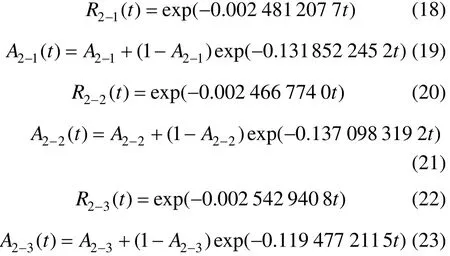

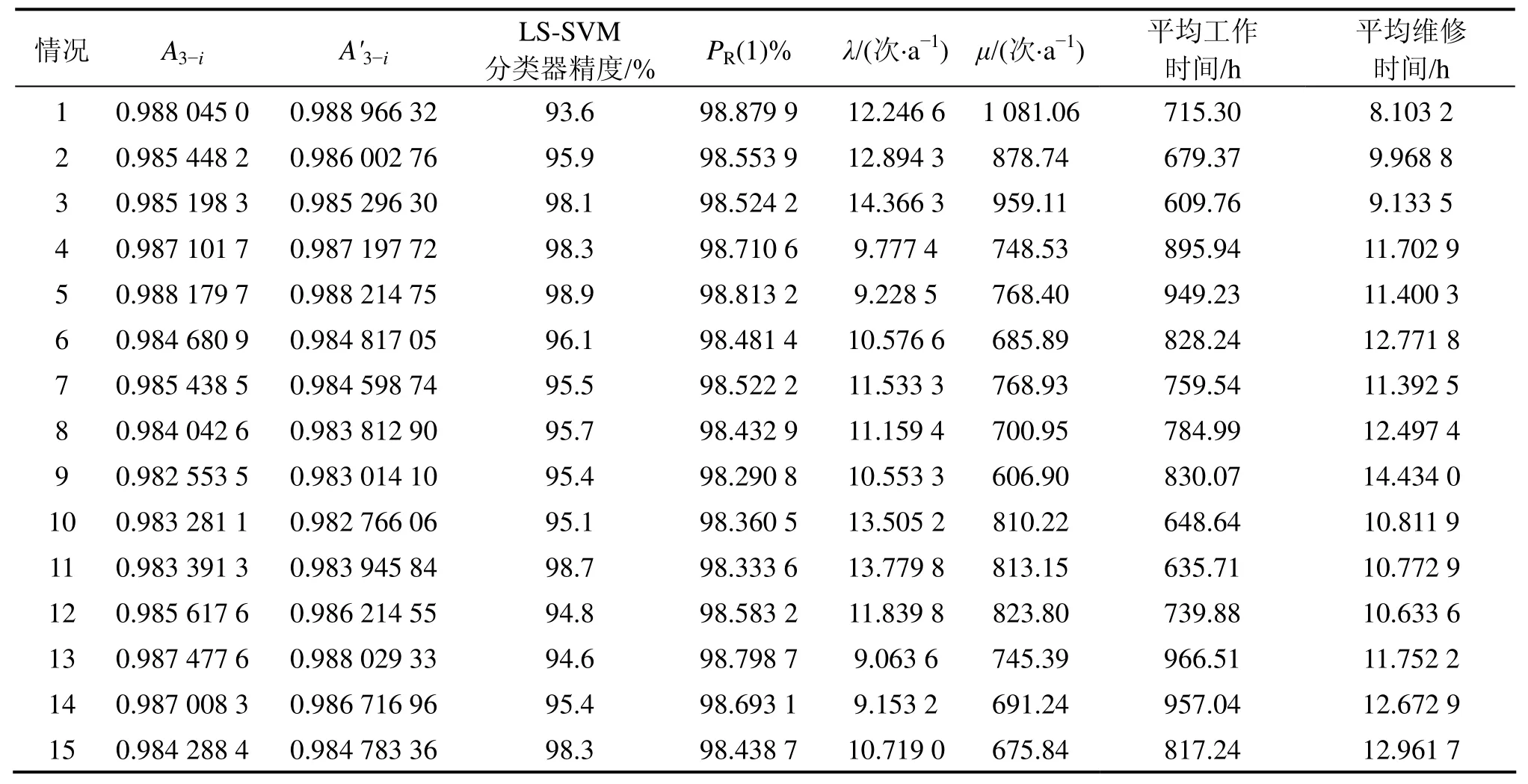


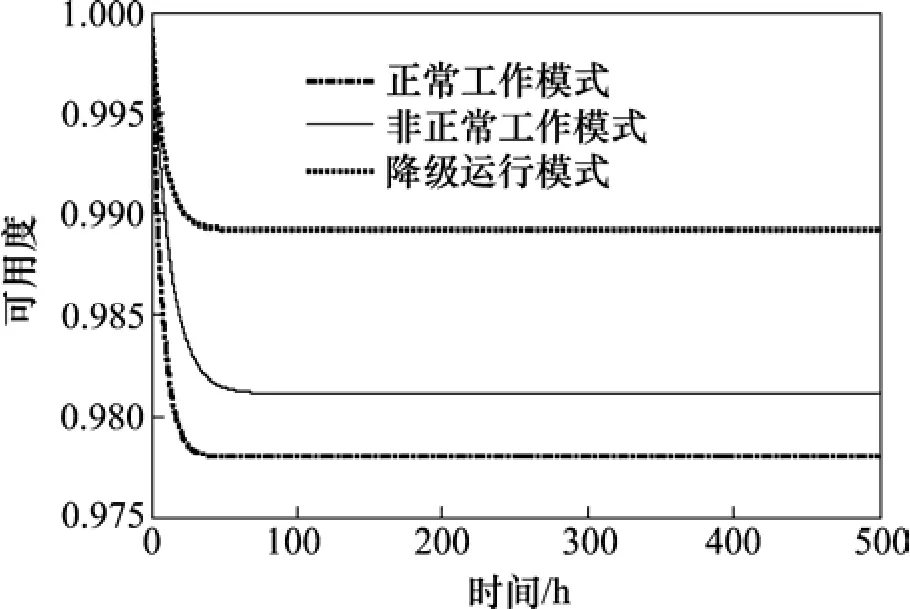
3.5 几种工作模式的对比分析
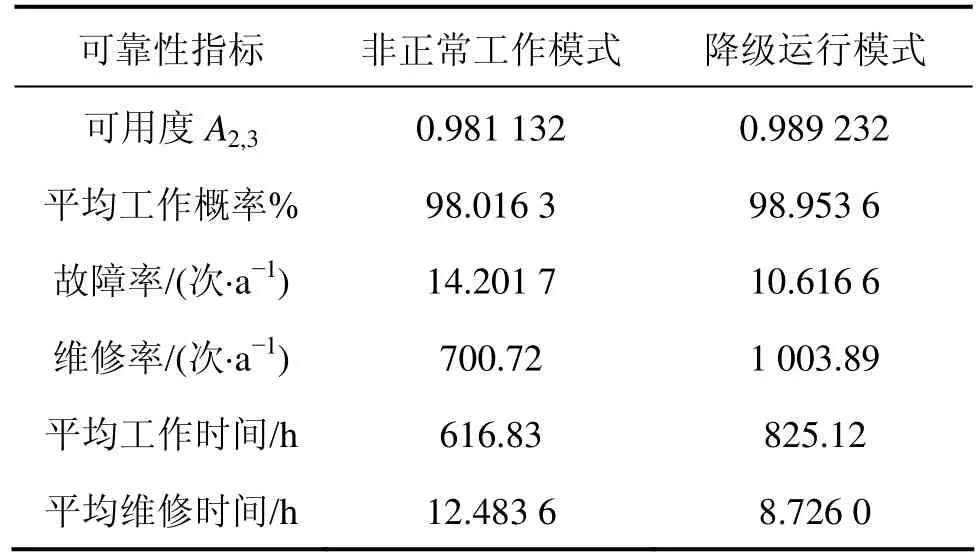

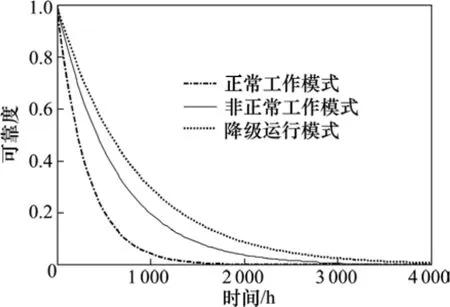
4 结论
