低惯量后梁的创新设计
2018-05-23金亮周巧燕
金亮, 周巧燕
(1.浙江理工大学 现代纺织设备重点实验室,杭州 310018;2.万利纺织机械研究院,杭州 311243)
0 引言
后梁结构是织机送经系统中重要组成部分,目前多采用双后梁结构,即一根固定后梁和一根活动后梁。其中,固定后梁可用于支持经纱并改变经纱方向,活动后梁可缓解由于织机开口、打纬等运动造成的经纱张力波动,同时可感知经纱张力的改变并对其作出响应,该响应特点会影响织造效率及织物品质。但当织机主轴转速较高时,活动后梁摆臂摆动频率加快,由于活动后梁自身重量较大,将产生较大惯性力,不能对经纱张力的变化做出及时响应,经纱张力瞬时波动无法得到有效的缓解。目前,研究剑杆织机后梁的学者比较多,涉及到后梁系统的结构参数与经纱路径关系的研究[1],后梁机构的调整与改进[2-3],积极式活动后梁机构的研究,后梁机构动静态载荷特性的分析[5-6],松经装置的研究[7-9],活动后梁力学模型的建立以及经纱张力分布特点的研究[10-14],但很少涉及到低惯量后梁以及变刚度后梁结构创新设计方面的研究。
针对传统后梁所存在的问题,提出一种新型后梁结构,说明其结构组成以及工作原理,对关键零部件进行详细的设计并说明设计意图。分析其性能特点及该结构的优势,为低惯量后梁结构的优化设计和后续深入研究提供依据。
1 传统后梁
1.1 传统后梁结构
以浙江万利纺织机械有限公司生产的WL450型剑杆织织机为例,机构简图见图1,经纱2从经轴1上退绕出来,经过固定后梁3、活动后梁4、停经架7、综框8到达织口O,再进入卷取系统。固定后梁3铰接于机架O1点处,后梁摆臂5一端铰接于机架O2点处,另一端与弹簧6铰接于E点,中部与活动后梁4铰接于O3点,弹簧6借助滑块铰接于机架O4点。

图1 传统后梁结构经纱和织物走向图
1.2 后梁系统功能特点
织机中的后梁结构具有检测并缓解经纱张力的作用。后梁结构对于经纱张力变化的响应能力与自身结构相关,且该响应能力对经纱张力的缓解有重要意义。
传统后梁结构主要由固定后梁、活动后梁、活动后梁摆臂、弹簧所组成。固定后梁3可稳定经纱在活动后梁上的包角,以减少经轴直径的变化对活动后梁的影响。活动后梁摆臂可以O1为圆心摆动,当经纱张力因开口等运动发生改变时,活动后梁摆臂可带动活动后梁相应旋转,同时弹簧6压缩或者回弹。经纱路径随之改变,从而达到缓解经纱张力的作用。弹簧6用来平衡经纱张力、活动后梁自身重力以及活动后梁的惯性力。这种后梁可利用活动后梁摆臂的旋转改变经纱路径,进而缓解经纱张力变化,使经纱张力变化趋于平缓[1]。
但是这种后梁有一定缺点:当织机门幅较宽时,活动后梁为了满足刚度要求,一般情况下重量都较重,当织机转速相对较高时,活动后梁往复摆动频率高,惯性力大,活动后梁来不及对经纱张力的改变做出及时响应,不能很好地缓解经纱张力波动,影响织物的品质和效率。为了宽幅或高速织机活动后梁能快速及时响应开口或打纬等高频动作引起的经纱张力瞬间波动,设计一种低惯量后梁结构,减少高速织造过程中经纱张力的瞬时波动。
2 低惯量后梁
2.1 低惯量后梁结构组成
如图2所示,由板簧活动后梁1,弯形板簧2,直形板簧3,弹性介质4,垫块5,支撑架6,固定后梁7组成低惯量后梁系统。固定后梁7与支撑架6固连,且固定后梁7与6连接处设有长槽;板簧活动后梁1作为一个整体横跨于整个织机门幅;若干个弯形板簧2和直形板簧3以一定间距固定在支撑架6上,支撑架6是一个整体;弯形板簧2、板簧活动后梁1、直形板簧3,三者于a点固定连接;弹性介质4与支撑架6上的垫块5固连,弹性介质4数量与弯形板簧2数量相等,其位置与弯形板簧2(直形板簧3)位置对应。

图2 低惯量后梁织机经纱与织物走向图
2.2 工作原理
经纱从经轴9退解后经过固定后梁7、板簧活动后梁1到达综框,参与织造。当经纱张力由于开口等原因发生变化时,板簧活动后梁1受到经纱张力的作用并迫使弯形板簧后梁2(3)发生弯曲形变。弯形板簧2的形变使板簧活动后梁1位置改变,进而改变经纱路径,从而缓解经纱张力的变化。
经纱张力变化的缓解主要靠弯形板簧2,直形板簧3的自身弹性变形进而改变经纱路径来实现的,固定后梁7可稳定经纱在活动后梁上的包角。当织造需要经纱张力较大时,可调节弹性介质4的位置,与弯形板簧(直形板簧)接触,增大其刚度,减小板簧活动后梁的位置变化量。
2.3 主要零部件设计
2.3.1 板簧活动后梁
板簧活动后梁主要作用是让经纱在其上表面经过,支持经纱并且承受经纱张力。如图3所示,板簧活动后梁上部为类圆弧状,下部有螺钉孔可与弯形板簧,直形板簧连接。由于其上表面与经纱接触,表面光洁度要求较高,且需要耐磨。
2.3.2 弯形板簧

图3 板簧活动后梁结构
在新型后梁结构中,弯形板簧的弹性变形对于改变经纱路径,缓解经纱张力意义重大。如图4所示,弯形板簧为变截面梁,且分为上下两部分。下部形为等腰梯形,上部为弯曲结构。上部的弯曲结构端部可顶靠在板簧活动后梁内侧,因此可增大板簧活动后梁刚度。使得后梁的变形主要依靠弯形板簧而不是板簧活动后梁。变截面梁的设计可使梁的抗弯刚度从下至上逐渐递减,使得在经纱张力作用下,下部可牢固连接而且有利于增大上部的变形量。
2.3.3 直形板簧
对于改变经纱路径,缓解经纱张力,直形板簧的弹性变形也同样重要。如图5所示,直形板簧结构与弯形板簧结构类似。直形板簧可叠放于弯形板簧一侧从而增加弯形板簧的刚度,可以增加或者减少直形板簧的数量以调节弯形板簧的刚度。

图4 弯形板簧结构
2.4 性能讨论
以WL450型门幅为540 cm剑杆织机为例,表1所示为传统活动后梁和板簧活动后梁结构参数。

图5 直形板簧结构
织机工作过程中,活动后梁受到自身重力以及经纱张力作用会产生弯曲变形,后梁各处变形的均匀程度会影响各处经纱路径,进而影响织物品质。由于传统活动后梁只有两端铰支,而板簧活动后梁以一定间距分段铰支,固将两种活动后梁可简化如图6所示。
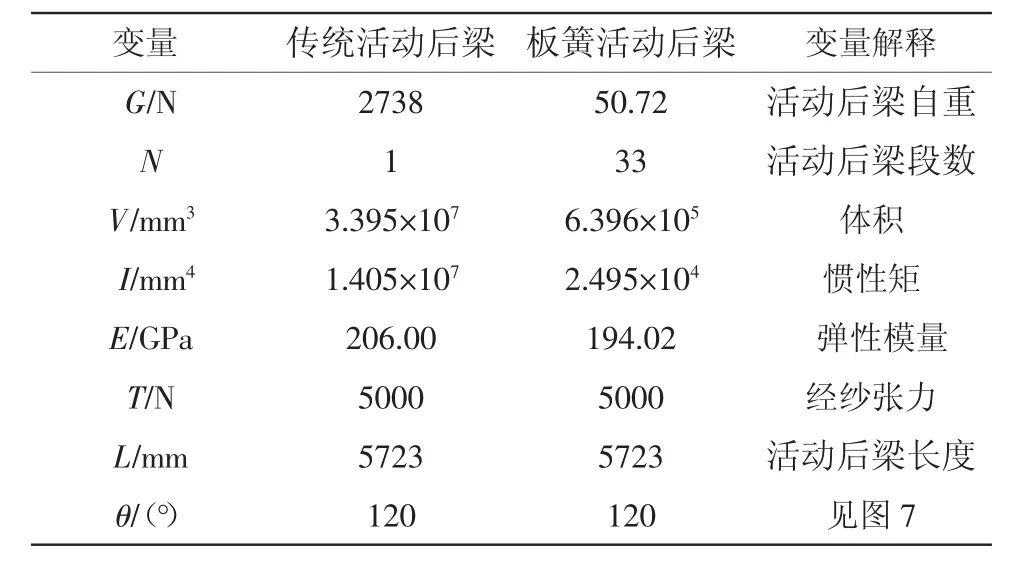
表1 原始参数表
其中:q1为传统活动后梁重力集度;q2为经纱合力集度;q3为板簧活动后梁重力集度。
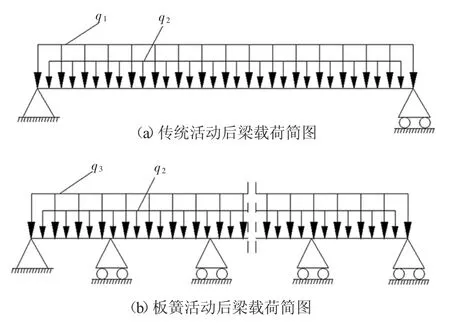
图6 两种活动后梁载荷简图
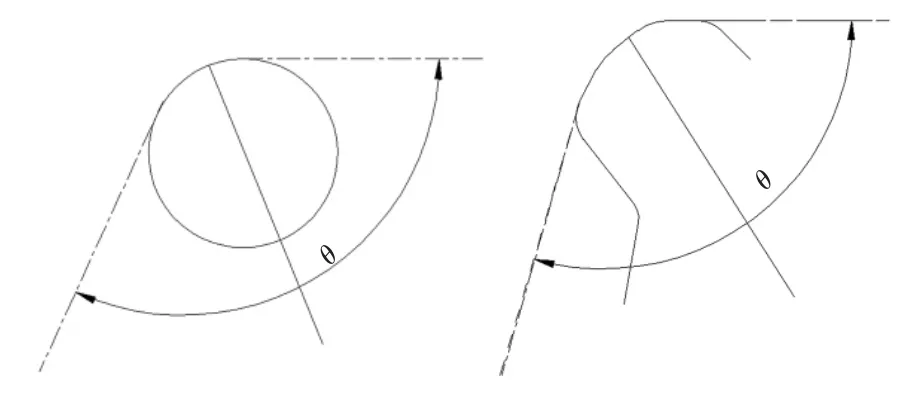
图7 纱线包绕活动后梁图
重力集度为
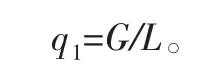
经纱合力集度为

利用挠曲线方程[15]可求得传统活动后梁在重力作用下的最大挠度(梁中点处挠度)为

同理,传统活动后梁在经纱张力作用下的最大挠度(梁中点处挠度)为

将传统活动后梁的参数带入式(1)、式(2)中,得到f1=2.308 mm,f2=4.215 mm。
由于板簧活动后梁各段载荷相同,故只分析其中一段即可。板簧活动后梁在重力作用下的最大挠度(梁中点处挠度)为

板簧活动后梁在经纱张力作用下的最大挠度(梁中点处挠度)为

将板簧活动后梁的参数带入式(3)、式(4)中,得到f3=2.14×10-5mm,f4=0.0696 mm。
由于f3、f4远远小于f1、f2,可知同样载荷条件下,与传统活动后梁相比,板簧活动后梁变形量更小且更均匀。而且板簧活动后梁体积小,更加节省空间。
3 结论
针对传统后梁结构存在的问题,设计出一种新型的后梁结构。板簧活动后梁、弯形板簧、直形板簧三种构件相互拼合而成以及弹性介质的使用,可方便调整后梁系统刚度,从而适应更多织物种类。而传统后梁的弹性元件只有弹簧,故其适应的织物种类范围与新型后梁相比必定较小。
当织机门幅较宽时,同样载荷情况下,板簧活动后梁直线度远远好于传统活动后梁,经纱路径变化同步性更好,该特性对织物品质有重要意义。
板簧重量远比传统活动后梁重量轻,即使织速较高,弯形板簧后梁(直形板簧后梁)弹性变形频率较快时,其惯性力远小于传统活动后梁的惯性力。所以相对传统后梁而言,没有了过大惯性力的影响,该后梁能够对经纱张力的改变做出更及时的响应,能更好地缓解经纱张力的瞬时波动,提高织造效率以及改善织物品质。
[参考文献]
[1] 周香琴,刘宜胜.织机开口引起的经纱张力变化规律[J].纺织学报,2014,35(5):153-158.
[2] 陈革,孙志宏,陈明.织机后梁系统的研究[J].东华大学学报(自然科学版),2001,27(1):41-43.
[3] 贺斌,姚景宏.G1820型喷气织机后梁的设计[J].机械工程与自动化,2003(4):33-34.
[4] 周骏彦.伺服驱动技术在织机电子送经与卷取的应用[J].上海纺织科技,2008,36(9):13-16.
[5] 丁辛.织机后梁动态性能分析[J].中国纺织大学学报,1993,19(2):58-62.
[6] 王斯勇,冯志华,孙浪,等.喷气织机单双后梁系统动态分析与比较[J].苏州大学学报(工科版),2010,30(1):56-59.
[7] 董敬宇.ZA200系列喷气织机松经机构对经纱张力的影响分析[J].纺织器材,1996,26(5):24-27.
[8] 刘忧华.喷气织机松经机构与后梁配合的应用探讨[J],化纤与纺织技术,2015,44(1):40-44.
[9] 杨晔,冯志华.喷气织机松经装置改进与经纱张力控制[D].上海:东华大学,2011.
[10] 杨文强,陈家新.髙速喷气织机经纱动张力特性及控制技术[D].上海:东华大学,2013.
[11] CHEN Ge,MAO Liming,ZHOU Yaqin,et al.Study on the back rest system of looms[J].Journal of Donghua University,2004,14(1):109-111.
[12] 来震.织机经纱张力模型的建立和分析[J].丝绸,2004(8):34-37.
[13] 陈家新,宋楠,白洋,等.织机经纱动态张力分布特征研究[J].纺织机械,2013(1):40-45.
[14] 吴飞青,马修水,关宏伟,等.基于模糊专家控制的织机经纱恒张力控制研究[J].中国机械工程,2008,19(4):384-387.
[15] 刘鸿文.材料力学[M].北京:高等教育出版社,2008.
