开端情况下自紧身管应力分布简化计算数值仿真
2018-05-23杜中华
杜中华
(军械工程学院,石家庄 050003)
0 引言
自紧身管通过制造时在身管内膛施加高压,使身管内壁发生塑性变形,高压撤除后,在身管内壁产生残余应力,这些残余应力可以使身管在发射时承受更高的膛压,从而提高身管的强度。目前高膛压火炮普遍采用自紧身管[1-4]。
由于自紧身管制造时材料要发生塑性变形,研究自紧身管应力分布通常采用第三强度理论(Tresca准则)和第四强度理论(Mises准则)。采用第四强度理论时由于要考虑轴向应力,又分为开端和闭端等不同情况。开端情况下(平面应力,如图1所示)的应力表达式十分复杂,为了便于工程应用,文献提出采用修正屈服准则来代替Mises屈服准则[3-4]。为考察这种代替的误差大小,本文用数值仿真方法对2种屈服准则下的应力分布进行了比较研究。

图1 开端平面应力情况

图2 自紧身管截面
1 基于Mises屈服准则的开端自紧身管应力分布理论
假定自紧身管某截面内半径为a,外半径为b,自紧半径为ρ,则自紧度为如图2所示。材料采用理想弹塑性模型,材料屈服极限为σs。由厚壁圆筒理论,3个主应力为:σt、σr和σz。
对于开端情况,σz=0。故mises屈服准则为
应力分析主要考察任意半径r处的压力p和
弹塑性交界处
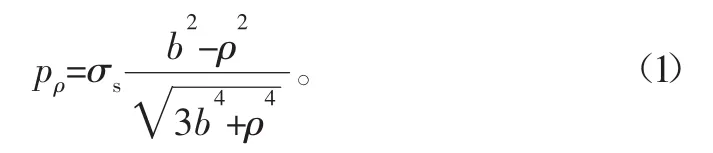
弹性区(ρ≤r≤b)

塑性区(a≤r≤ρ)
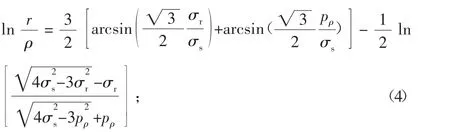

塑性区的p=-σr要由式(4)求得,鉴于式(4)的复杂性,工程上应用不便,文献提出用修正屈服准则来代替mises屈服准则可满足工程应用需要。
要指出的是,借助式(4)求出身管的自紧压力——身管强度也十分困难。
2 基于修正屈服准则的开端自紧身管应力分布理论
代替mises屈服准则的修正屈服准则为σt-σr=1.08σs。
由该准则,在弹塑性交界处:

弹性区(ρ≤r≤b)

塑性区(a≤r≤ρ)

由式(9)可知对应自紧半径ρ的自紧压力:
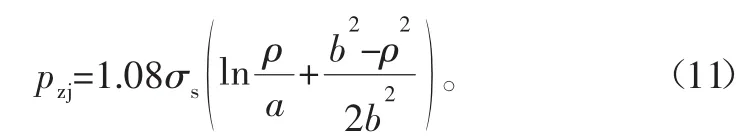
应指出的是,上面的修正屈服准则和Tesca屈服准则相近,工程上对tresca屈服准则的修正也采用同样的形式。
3 两种准则下数值仿真研究
实际上,对于复杂的式(4)完全可以借助Matlab中的数值求解方法进行求解[5],这也是本文开展研究的基础。某型火炮自紧身管毛坯典型截面的内半径为90 mm,外半径为160 mm,自紧半径130 mm,自紧度约0.57,材料屈服极限为1100 MPa。为了便于比较,利用上面公式分别计算身管各半径处的p和q,q定义为屈服指标,采用mises屈服准则采用修正屈服准则时
计算中为了确保对式(4)求解的正确性,对求得的解代入式(4)进行了验算。残余应力是用制造应力减去附加应力获得的,附加应力是身管内部承受自紧压力且假定身管只发生弹性变形的应力,其计算理论详见文献[1]~[3]。
数值仿真得到制造时身管管壁各半径处应力分布曲线分别如图3和图4所示。可以看出,两种准则下弹性区的p和塑性区的q是基本一致的。但是弹性区的q存在一定误差,越靠近身管外表面误差越大,外表面处修正准则比mises准则减小了7.3%。误差最大的应力是塑性区的p,越靠近身管内表面误差越大,身管内表面处修正准则比mises准则增大了33.8%。身管内表面的p就是自紧压力,它决定了自紧身管能够承受的最大内压强,实际上就是自紧身管的强度。对于该例,按照mises准则,身管该截面强度为477 MPa,而按照修正准则,身管该截面的强度将达到639 MPa,两者相差很大。高压撤除后,身管壁内残余应力的分布分别如图5和图6所示,可以看出两种准则下,残余应力差别也相当大。

图3 制造时p分布曲线

图4 制造时q分布曲线

图5 制造后p分布曲线

图6 制造后时q分布曲线
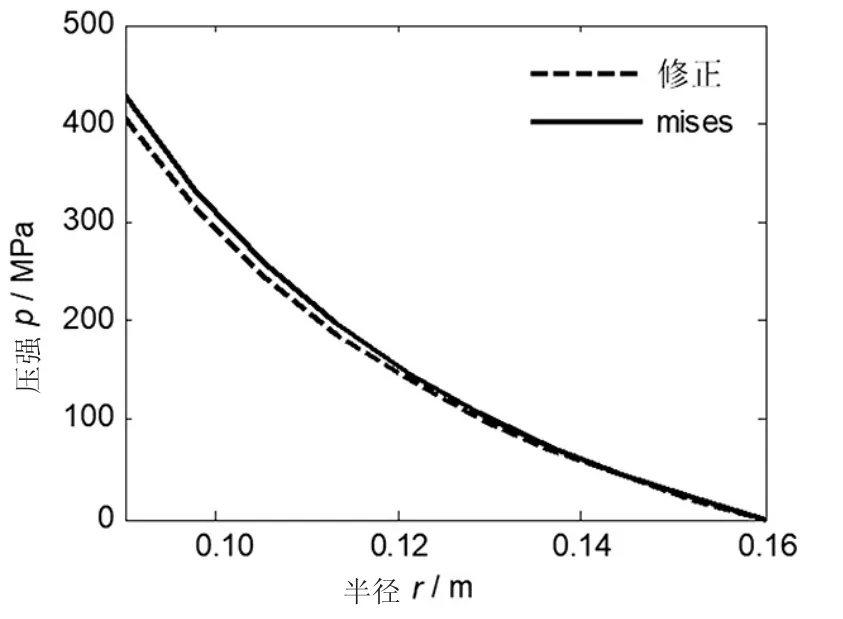
图7 制造时p分布曲线(ρ=90 mm)
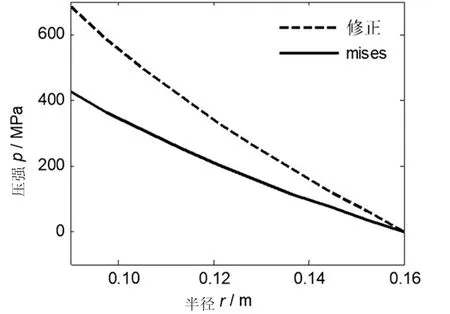
图8 制造时p分布曲线(ρ=160 mm)
将该例中自紧度分别更换为0(ρ=90 mm)和1(ρ=160 mm),即单筒身管和全塑性自紧身管的情况,此时得到制造时p分布曲线分别如图7和图8所示。可以看出,自紧度为0时,修正准则相对mises准则身管强度减小5%,自紧度为1时,修正准则相对mises准则身管强度增大61%。这说明用修正准则代替mises准则只在自紧度为0附近误差较小,自紧度越大,误差越大。文献中关于用修正准则代替mises准则可以满足工程中应用的精确性说法是值得商榷的。
4 结论
采用第四强度理论研究开端自紧身管应力分布时,考虑到塑性区压强的计算公式十分复杂,文献指出用修正屈服准则代替mises准则可以满足工程中应用的精确性。
本文借助数值仿真方法对两种准则下的应力情况进行了分析,对某型身管截面的计算表明,当自紧度分别为0、0.57、1时,修正准则相对mises准则计算出的身管强度分别减小5%、增大33.8%、增大61%。鉴于两者之间存在较大的误差,故用修正准则代替mises准则用于工程实际可能存在一定的问题。
[参考文献]
[1] 张相炎,郑建国,袁人枢.火炮设计理论[M].北京:北京理工大学出版社,2014.
[2] 潘玉田.炮身设计[M].北京:兵器工业出版社,2007.
[3] 曾志银,张军岭,吴兴波.火炮身管强度设计理论[M].北京:国防工业出版社,2004.
[4] 才鸿年,张玉诚,徐秉业,等.火炮身管自紧技术[M].北京:兵器工业出版社,1997.
[5] 薛定宇,陈阳泉.基于Matlab/Simulink的系统仿真技术与应用[M].北京:清华大学出版社,2002.
