各向异性度对水平井井壁稳定性的影响

肖钦萍，贺云婷，何雅文

（1.西安石油大学机械工程学院，陕西西安 710065；2.西安石油大学石油工程学院，陕西西安 710065）

在钻井过程中由于原位应力场，往往存在力学稳定性问题，因此需要进行井壁稳定力学研究[1]。在以往的工程设计中，往往粗略的将岩体近似为各向同性体，这对于浅部地层来说是合理的；但是随着钻井深度的增加，深度井井壁围岩表现出强烈的各向异性特性从而导致井壁失稳，此时采用简单的各向同性应力方程已经不能满足安全钻井的要求[2，3]。在各向异性地层井壁应力分布研究方面，Lekhnitskii、Amadei、Aadnoy 和Ong[4-7]建立了考虑各向异性介质的井壁应力计算模型；衡帅等[8]研究了岩石的力学特性、强度特性和破裂模式的各向异性，给出了横向各向同性体的五个材料参数；王汉等[9]建立了各向异性岩石的井壁应力计算模型，分析了岩石力学参数各向异性对井壁应力分布的影响；王倩等[10]通过实验和理论计算的方法验证了各向异性度可评价岩石的各向异性程度。但是这些研究都没有进一步分析各向异性度对井壁稳定性的影响，鉴于此，本文基于层理地层岩石力学特性，用Matlab软件获得了各向异性度对水平井壁应力分布的规律，然后通过考虑拉伸失效准则和剪切失效准则来研究各向异性度对水平井壁稳定性的影响。

1 各向异性度

各向异性度k定义为层理面的杨氏模量E与垂直于层理面的杨氏模量E'之比，即k＝E/E'，即k=1为各向同性。各向异性度越大，各向异性的程度越高，不同的材料其各向异性度也不一样。

2 各向异性度对水平井壁应力分布的影响

当井眼轴线平行于最大主应力方向，作用在水平井壁上两个相互垂直的σv和σh，min之间的值差异较大时，各向异性度对水平井壁应力分布的影响较为突出[11]，所以本文在建立的横向各向异性岩石水平井壁应力分布模型的基础上，只计算此种情况下水平井壁应力分布情况。取最大水平地应力σh，max=45 MPa，最小水平地应力 σh，min=35 MPa，上覆地应力 σv=70 MPa，αb=45°，βb=90°，αs=ατ=0°，βs=45°，βτ=30°，弹性模量 E=31.75 GPa，泊松比v=0.28，钻井液液柱压力pw=45 MPa。

由于进行井壁稳定性分析时，只用到最小主应力，所以这里只分析水平井壁上的情况。最小主应力分布用圆柱坐标系画出（见图1）。由于图1关于中心对称，所以分析图形时只讨论井周角θ在0°～90°这部分圆弧。从图1可以观察到：最小主应力受各向异性度的影响较小。只有当θ在0°～20°时，对于不同的各向异性度最小主应力的值才存在差异，各向异性度越大，其最小主应力的值越小，θ=0°时最小主应力的值最小；θ≥20°时，对于不同的各向异性度最小主应力的值近乎一样。

考虑了不同各向异性度水平井壁处的切应力分布图（见图2）。切应力分布图关于中心对称，所以分析图形时也只讨论井周角θ为0°～90°这部分圆弧。从图2可以观察到：当θ角接近0°和 90°时，各向异性度越大其切应力的值越小；当θ=0°时切应力总是最小的，θ=90°时切应力总是最大的；每四分之一个圆弧上切应力曲线有两个交点，第一个交点大约在θ=20°处相交，相交之后各向异性度越大其切应力的值越大；第二个交点大约在θ=60°处相交，相交之后各向异性度越大其切应力的值越小；当k≥4时，切应力曲线近乎一致。

3 水平井壁稳定性分析

分析了水平井壁处的主应力分布和切应力分布，还需要进一步分析水平井壁在该应力状态下是否稳定。当作用在井壁上的应力状态超过地层强度时，认为井壁开始失效，在进行水平井壁稳定性分析时通常只关注拉伸失效和剪切失效[12]。

图1 井壁处的最小主应力分布

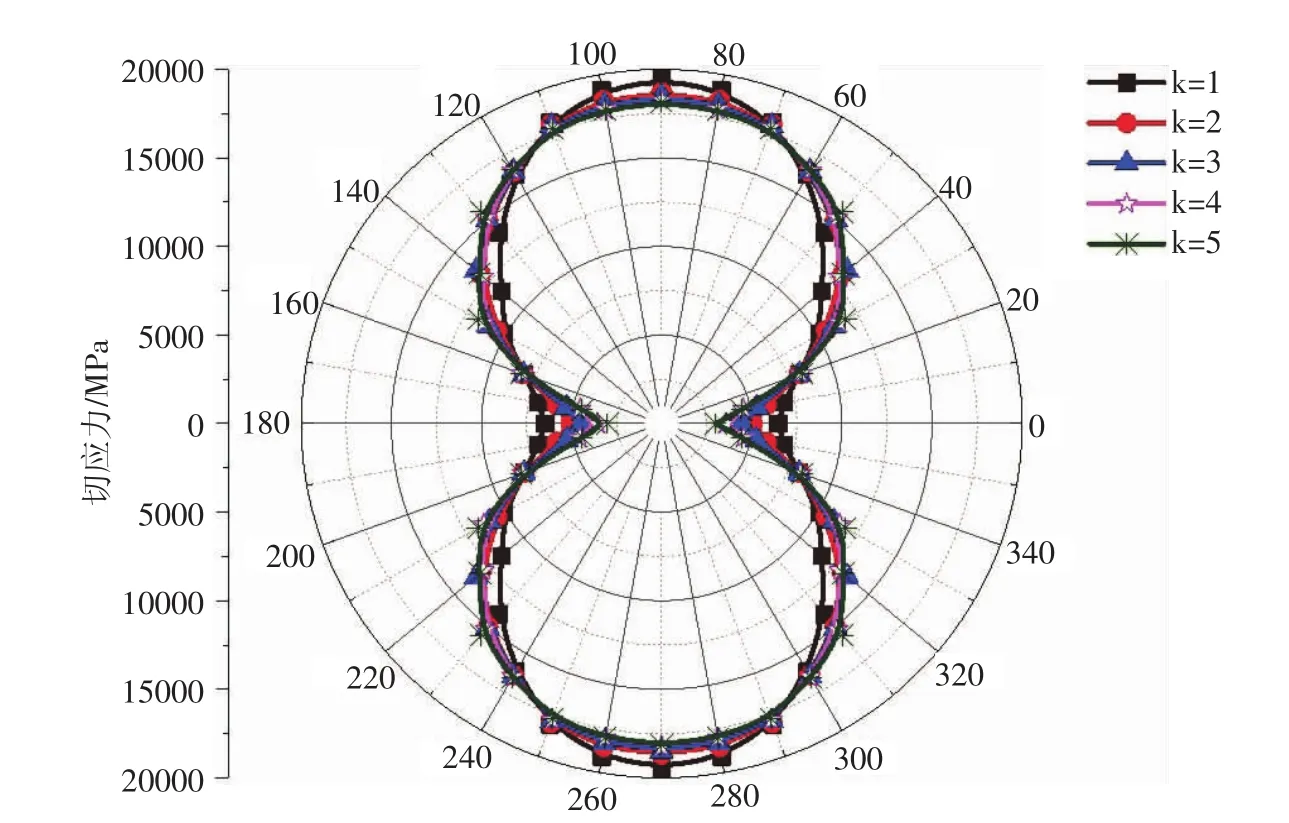
图2 井壁处的切应力分布

拉伸失效准则选用最大主应力强度理论来分析水平井壁稳定性，只要一个主应力达到岩石的抗压强度或者岩石的抗拉强度，岩石便失效。井壁的拉伸破坏通常是由最小主应力来定义的，所以本文用最小主应力与岩石的抗拉强度来做比较。而常用的剪切失效准则有Mohr-Coulomb准则、Tresca's准则、Lade准则和Drücker-Prager准则，Mohr-Coulomb 准则是使用时间最长和最常用的准则，本文选用Mohr-Coulomb准则分析水平井壁稳定性。

3.1 拉伸失效准则

当井壁处的最小主应力大于或等于岩石的拉伸强度时，岩石开始失效，即当σ3≥-σt时，发生失效。

当θ=0°时最小主应力达到最小值，所以只分析θ=0°时不同各向异性度的最小主应力曲线。不同各向异性度的拉伸失效准则曲线（见图3），水平黑线在纵轴上的值为岩石的拉伸强度，如果最小主应力在黑线对应值的下方，表明水平井壁拉伸失效。从图3可以观察到：当k≤2时，对于任何方位角α，水平井壁都是稳定的；当k=3时，水平井壁在α为0°～20°时发生拉伸失效，α为20°～90°时稳定；当k=4时，水平井壁在α为0°～30°时发生拉伸失效，α 为 30°～90°时稳定；当 k=5 时，水平井壁在 α 为 0°～40°时发生拉伸失效，α 为 40°～90°时稳定；当k≥3时，随着各向异性度的增加，水平井壁发生拉伸失效的角度在逐渐增大。

3.2 剪切失效准则

剪切失效准则为[13]：

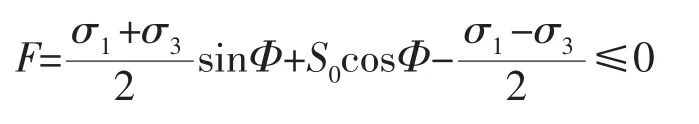
其中Φ为内摩擦角，当F≤0时发生失效。

当θ=90°时切应力达到最大值，所以只分析θ=90°时不同各向异性度的切应力曲线，不同各向异性度的Mohr-Coulomb失效准则曲线（见图4），根据Mohr-Coulomb失效准则，F≤0时发生剪切失效。从图4可以观察到：对于k=1的情况，大约在α≤35°时水平井壁发生剪切失效，α≥35°时水平井壁稳定，所以用k=1假设获得的井壁稳定性预测仅适用于α≥35°的情况；当k≥2时井壁不发生剪切失效，并且随着各向异性度的增加，曲线远离失效线（F=0）。

图3 不同各向异性度的拉伸失效准则曲线

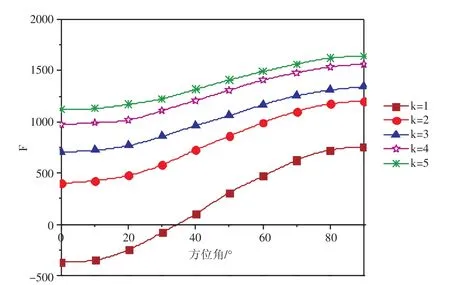
图4 岩石不同各向异性度的Mohr-Coulomb失效准则

4 结论

（1）最小主应力在 θ为 0°～20°时，各向异性度越小，其应力分布越接近k=1的应力分布，随着各向异性度的增加，其应力分布与k=1的应力分布之间的差距增大；θ≥20°时不受各向异性度的影响，其应力分布与k=1的应力分布一致。所以在实验中确定各向异性度时务必谨慎，以提高稳定性预测的准确性。

（2）当各向异性度 k≤2，α≥35°时水平井壁既不发生拉伸失效也不发生剪切失效，这时岩石可以做各向同性假设；随着各向异性度k的增加，井壁的拉伸失效趋势增加，而剪切失效趋势减小。

参考文献：

[1]陈勉，金衍，张广清.石油工程岩石力学[M].北京：科学出版社，2008.

[2]Lajtai E.Z.Strength of discontinuous rocks in shear[J].Geotechnique，1969，19（2）：218－233.

[3]陈新，杨强，何满潮，等.考虑深部岩体各向异性强度的井壁稳定性分析[J].岩石力学与工程学报，2005，24（16）：2882－2888.

[4]Lekhnitskii，S.G.Theory of Elasticity of an Anisotropic Body[M].Trranslated by Fem P.San Francisco，Holden－Day lne，1963.

[5]Amadei B.In situ stress measurements in anisotropic rock[J].International Journal of Rock Mechanics and Mining Science&Geomechanics Abstracts，1984，21（6）：327－338.

[6]Aadnoy B S，Chenevert M E.Stability of highly inclined boreholes[J].SPE Drilling Engineering，1987，2（4）：364－374.

[7]Ong S H.Borehole stability[M].Norman：University of Oklahoma，1994：201－210.

[8]衡帅，杨春和，张保平，等.页岩各向异性特征的试验研究[J].岩土力学，2015，36（3）：609－616.

[9]王汉，陈平，张智.页岩力学参数各向异性对井壁应力分布的影响[J].长江大学学报（自然版），2015，12（20）：41－46.

[10]王倩，王鹏，等.页岩力学参数各向异性研究[J].天然气工业，2012，32（12）：62－65.

[11]BHARGAVA R，SHARMA K.A study of finite size effects on cracked 2-D piezoelectric media using extended finite elementmethod [J].ComputationalMaterialsScience，2011，50（6）：1834-1845.

[12]Mclean，M.R.，&Addis，M.A.Wellbore stability：The effect of strength criteria on mud weight recommendations[J].SPE Annual Technical Conference and Exhibition，1990：23－26.

[13]Yi，X.，Russell，J.E.，&Ong，S.H.Improving Borehole Stability Analysis by Quantifying the Effects of Intermediate Principal Stress using Polyaxial Rock Strength Test Data[M].The 40th U.S.Symposium on Rock Mechanics（USRMS），Anchorage，AK，2005.