面板堆石坝的渗流监测模型研究
2018-05-22张海龙殷建峰仇建春周明明
张海龙 殷建峰 颜 蔚 仇建春 周明明
(1.河海大学 水利水电学院,南京 210098;2.河海大学 水资源高效利用与工程安全国家工程研究中心,南京 210098;3.河海大学 水文水资源与水利工程科学国家重点实验室,南京 210098;4. 无锡市水利设计研究院有限公司,江苏 无锡 214023;5. 江苏省江都水利工程管理处,江苏 扬州 225200)
面板堆石坝是以堆石体为主体,并在其上游表面设置面板作为挡水防渗的一种堆石坝.当坝体发生变形产生混凝土面板开裂,或者周边缝发生破损或破坏,上游库水将会对坝体产生渗透作用,考虑到堆石体主要为松散堆积体组成,面板堆石坝出现渗透破坏将对坝体变形、结构和安全产生负面影响.因此,对面板堆石坝展开渗流监测与分析具有重要的意义.为正确及时的分析和监控大坝的渗流状态,需要建立渗流监控安全模型,以便发现大坝渗流隐患,从而确保大坝的安全稳定运行[1].影响面板堆石坝渗流状态的因素有库水位、降雨、温度、时效等,目前对面板堆石坝的渗流监控模型仅限于统计回归模型,岑黛蓉[2]研究了面板堆石坝各部分及整体的渗流场特性,根据坝工理论,推导了库水位分量、降雨分量、温度分量和时效分量的数学表达式,建立了面板堆石坝的渗流监控统计模型,并在那兰面板堆石坝的渗流安全监控中取得了较高的精度;徐镇凯[3]等针对库水位与降雨对面板堆石坝渗流影响的滞后效应,在综合考虑覆盖层厚度、筑坝材料对大坝渗流影响的基础上,建立了考虑滞后效应的面板堆石坝渗流安全监控模型,该模型不仅较好地反映库水位、降雨对渗流的滞后影响,模型精度及预测效果也优于一般的渗流统计模型.而大坝渗流监控模型的方法还包括神经网络和模糊数学等.为此,本文首先研究建立了考虑库水位和降雨滞后效应[4-5]的面板堆石坝渗流监控模型,并用量子遗传优化算法求解得出了最优的滞后效应参数.然而,统计回归模型仅从显函数的角度进行监测分析了,实际上面板堆石坝渗流监测效应量所受影响因素复杂,难以用显函数常全面精确的模拟,鉴于小波神经网络模型的优势,可以克服显函数模型的困难,本文从隐函数角度建立了基于小波神经网络的面板堆石坝渗流监控模型.综合所建立两个模型的优势,在两者基础上,根据最大熵理论构建了面板堆石坝渗流监控组合式模型,该模型能够融合两个模型的优势,进一步优化面板堆石坝渗流监控模型.
1 考虑库水位和降雨滞后效应的面板堆石坝渗流统计模型
面板堆石坝的渗流状态受到库水位、降雨、温度及时效的共同作用,其中库水位和降雨对渗流的影响存在着滞后的效应,且影响基本服从正态分布.在采用正态分布曲线模拟滞后效应时,库水位和降雨对面板堆石坝渗流影响的滞后天数和影响天数不易确定,一般的计算方法计算效率较低.为此引用量子遗传优化算法[6],优化求解库水位与降雨的滞后天数和影响天数,得到最优的面板堆石坝渗流统计模型.
通过研究滞后效应的库水位和降雨分量,以及温度分量和时效分量,则面板堆石坝的渗流统计模型为:
H=hH+hP+hT+hθ+he=A0+aHd+bPd+

(1)

(2)
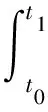

(3)
式中,A0为常数项;a,b为回归系数;x1为待定的水位滞后天数;x2为待定的水位影响正态分布标准差;H(t)为t时刻的实际库水位;x3为降雨滞后天数;x4为降雨影响分布参数;P(t)为t时刻的雨量;Pd为等效降雨量;β为入渗变换指数,0<β<1.
式(1)中的参数可以利用实测资料以模型的复相关系数和剩余标准差为目标函数,运用量子遗传优化算法,计算模型的因子系数和库水位、降雨的滞后参数,具体流程如图1所示.

图1 量子遗传算法优化流程
2 基于小波神经网络的面板堆石坝渗流监控模型
面板堆石坝渗流效应量与环境量之间关系复杂,难以用显函数来表达.神经网络算法能够在复杂关系中建立隐函数关系,并且具有较强的非线性拟合能力,自学习、自适应能力强,而小波变换是时间-频率的局部化分析,可以抓住实测数据的局部细节,更好的反映其特性.因此,本文结合小波分析和神经网络算法[7],建立基于小波神经网络的面板堆石坝渗流监控模型.
小波神经网络融合了神经网络算法和小波理论,具有多尺度分析和隐函数优势,由其建立的渗流监控模型能更客观的反映断层结构的渗流特性.其中神经网络结构与BP神经网络类似,隐含层结点的传递函数为小波基函数,通过误差反传来调整网络的权值阀值.具体的如图2所示.

图2 小波神经网络拓扑结构
图2中,X1,X2,…,X4为输入因子,分别为水压分量、降雨分量、温度分量、时效分量,Y为输出值,即为渗流效应量,wij和vj为权值.
当输入因子的数据序列为Xi(i=1,2,…,4)时,隐层输出为:
(4)
式中,h(j)为隐层第j个节点的输出值;wij为渗流因子输入层和隐层之间的权重;hj为小波基函数;bj为小波基函数hj的平移因子;aj为小波基函数hj的伸缩因子.
本文采用Morlet母小波,函数图像如图3所示,具体公式为:
(5)

图3 Morlet母小波基函数
渗流效应量的输出为:
(6)
式中,Y为输出的渗流效应量;其余参数的意义与式(4)、式(5)及图2相同.
3 基于最大熵的面板堆石坝渗流监控组合模型
上述两个面板堆石坝渗流监控分别从显函数及隐函数两个角度考虑了滞后影响下的库水位及降雨、温度因子及、时效因子;两个渗流监控模型各有其长处和缺点,渗流统计模型,在一定程度上反映了面板堆石坝的渗流状况,但渗流影响因素机理的复杂性常难以选择合理的显函数来反映;小波神经网络模型克服了这一缺陷,可以抓住实测数据的局部细节,从隐函数角度建立了面板堆石坝渗流监控模型.在两者基础上,本文应用最大熵原理[8],融合两个模型的优点,建立面板堆石坝渗流监控组合模型,对进一步把握面板堆石坝的渗流性态有积极意义.
一般的,将Shannon定义的熵称为信息熵,具体的表达式为:
(7)
式中,Pi为信息源中信号xi出现的概率;S(x)为熵值的大小,是系统状态不确定性的量度.
对于面板堆石坝渗流效应量,最大熵原理可以表示为如下优化问题:
(8)
约束条件为:
(9)

(10)
熵值最大时有:
(11)
式中,S(X)为渗流效应量X的熵;pi为渗流效应量X取值为xi时的概率;fk(xi)为X的函数,如一阶中心距、二阶中心距等;Fk为函数fk(xi)的均值;λk为拉格朗日乘子;k=1为渗流混合模型的情况,k=2为小波神经网络监控模型的情况.
面板堆石坝渗流监测效应量可以看作是随时间连续变化的离散序列,分别用基于量子遗传算法的渗流统计模型和基于小波神经网络的渗流监控模型对其进行预测,并计算预测值与实测值的偏差,将其作为预测量的约束信息,应用最大熵原理对这些约束信息进行求解,以达到提高模型预测精度的目的.具体的求解步骤如下:
1)模型特征值计算

(12)
2)最大熵概率密度函数求解
面板堆石坝渗流监测效应量X为离散型随机变量,根据最大熵原理,建立如下模型:
(13)
约束条件:
(14)

(15)
将式(23)代入式(26)和式(27)得:
(16)

(17)
联立式(27)和(28)可求得拉格朗日乘子λ0和λk(k=1,2)的值,即可以得到第i个实测值的概率函数为:
(18)
3)模型效应量预测

(19)
对概率进行积分求得期望值,即为这一天的预测值xt.然后重复步骤(3)即可得到T个面板堆石坝渗流的效应量预测值序列.
4 算例分析
4.1 工程概况
某水库控制流域面积326 km2,水库正常蓄水位115.13 m,校核洪水位为123.53 m,总库容1.14亿m3,防洪保护面积1.27万公顷,灌溉面积0.3万公顷,是一座综合的大(2)型水库.该水电站的渗流监测项目包括坝体测压管水位、坝基渗压、绕坝渗流和大坝渗漏量监测.
本文选取该面板堆石坝某测压管水位进行分析,建模时段为2011年1月1日至2011年12月31日,应用渗流监控模型拟合该测点的测压管水位,并用来预测2012年1月1日至2012年2月29日的渗流状态.图4及图5分别为2011年1月1日至2012年2月29日的降雨及库水位过程线.

图4 降雨监测资料

图5 库水位监测资料
4.2 监测模型在测压管监测中的应用
基于统计模型式(11),采用量子遗传算法,将库水位滞后与降雨滞后的影响参数优化求解,选取种群60个,以模型的复相关系数R为造适应度函数,求解出最优的统计模型.表1给出了测点统计模型的所求参数,包括滞后天数、复相关系数和均方根误差.

表1 统计模型求解的滞后参数及其复相关系数
小波神经网络模型的输入为等效的水位分量及降雨分量、温度分量、时效分量,输出为测压管水位的测值序列,其中温度分量按半年周期考虑,有4个因子,时效分量有2个因子,即8输入、1输出的结构,隐层结点数目选为6个结点,网络的拓扑结构为8-6-1.
通过对统计模型及小波神经网络模型的求解,模型对测点的拟合曲线如图6所示.可以发现,两者模型均有着较好的拟合效果,其中统计模型的均方根误差为0.572,小波神经网络的均方根误差为0.735.

图6 统计模型及小波神经网络模型的拟合效果
此外,将渗流统计模型及小波神经网络模型应用于对测压管水位2012年1月1日至2012年2月29日进行预测,在两者基础上,根据最大熵理论,通过对式(25)~(31)进行求解可以得到拉格朗日乘子λ0和λ1、λ2,其中λ1对应于面板堆石坝渗流混合模型,λ2对应于基于小波理论的面板堆石坝渗流监控模型.
对于预测序列,测点测压管水位的3个模型的预测值见表2.表3给出了3个模型的预测均方根误差.

表2 3个模型的预测值

表3 3个模型的预测精度
3个模型均有较好的预测精度,对比3种模型的预测结果,可以发现,基于最大熵理论将统计模型及小波神经网络模型融合,有着最小的均方根误差,即基于最大熵理论的面板堆石坝渗流监控组合模型的预测精度最高.
5 结 论
本文针对面板堆石坝渗流监测展开了3个模型监测试验研究,主要内容包括:
1)通过引入库水位和降雨的滞后天数和影响天数的概念,将水压分量、降雨分量进行等效处理,得到了等效水位和等效降雨.建立了面板堆石坝渗流的统计模型.
2)融合小波理论和神经网络模型的优势,建立了基于小波神经网络的面板堆石坝渗流监控模型,该模型具有高度的非线性映射能力,能反映渗流监测数据的细部特征.
3)针对单一模型的不足,利用最大熵原理,建立了组合监控模型,有效提高了面板堆石坝渗流监控模型的精度.
4)通过将3个监测模型应用于某面板堆石坝的测压管测点进行监测分析,发现3个模型有着较好的精度,其中组合模型融合了两个模型的优势,具有最优的精度,这相较于以往渗流监控模型精度有着进一步的提高,3个模型一起,成为一个整体,可为同类面板堆石坝的渗流监测提供技术支持.
参考文献:
[1] 徐 蔚.土石坝渗流监测资料分析方法的研究[D].杭州:浙江大学,2005.
[2] 岑黛蓉.覆盖层上面板堆石坝坝区渗流场特性及分析模型研究[D].南京:河海大学,2007.
[3] 徐镇凯,彭圣军,魏博文等.基于云自适应遗传算法的深覆盖层上面板堆石坝渗流监控模型研究[J].水电能源科学,2013,31(12):58-61.
[4] 仇建春,蔡婷婷,蒋 玮,等.大坝渗流统计模型在棉花滩水电站右岸绕坝渗流分析中的应用[J].水电能源科学,2013,31(5):49-51.
[5] 庞 琼,王士军,谷艳昌,等.基于滞后效应函数的土石坝渗流水位模型应用[J].水土保持学报,2016,30(2):225-229.
[6] 方国华,曹 蓉,刘 芹,等.改进遗传算法及其在泵站优化运行中的应用[J].南水北调与水利科技,2016,14(2):142-147.
[7] 江 婷,沈振中,徐力群,等.基于支持向量机-小波神经网络的边坡位移时序预测模型[J].武汉大学学报(工学版),2017,50(2):174-181.
[8] 孟 江.最大熵频谱分析与反褶积研究[D].西安:长安大学,2009.
