随机数据缺失条件下避税行为的逆威布尔渐近估计

余 萍

（1.中南财经大学 财政税务学院，武汉 430073；2.湖北经济学院 财政与公共管理学院，武汉 430205）

0 引言

政府为了保证国家机构的正常运行，需要通过征收税收的形式获取相应收入，通过把个人资源转移为社会资源，推动国民经济的良性循环，因此税收具有固定性、无偿性和强制性等特征。理性的企业为了追求利润最大化，往往通过合法的形式对政府的征税行为进行避税，企业的避税行为根据避税金额和避税频率的不同对社会造成的损害也会有所不同。很多学者对企业的这种避税行为进行研究，Lingert（2013）使用向量自回归模型对企业避税金额影响国民经济的情况进行实证研究，Poiere（2015）基于反事实法通过蒙特卡洛模拟对企业避税频率的社会危害进行分析。由于主客观等方面的原因，研究者无法获取企业经营的所有数据资料，为了更为准确地进行实证研究，研究者往往需要花费大量的人力、物力和财力进行数据搜集和整理，但很多情况下结果并不能让人满意。为了克服现有研究所存在的局限性，本文试图通过借鉴逆威布尔模型的基本思想，对企业避税行为周期进行数理推导，研究在数据缺失情况下逆威布尔模型对企业避税金额和避税频率估计参数的渐进一致性，并推导参数的置信区间。利用逆威布尔模型对企业避税行为周期进行蒙特卡洛模拟，检验模拟结果是否和随机数据缺失数量有关，分析模拟结果是否和企业避税金额大小及避税频率高低有关。各参数的模拟结果表明，模拟结果均处于相应置信区间内，且模拟结果不随随机样本数据缺失数目的变化而变化，也不因企业避税金额和企业避税频率的变化出现不一致情况。本文所构建的逆威布尔模型对企业避税行为周期的估计是渐进无偏的一致估计量，企业避税金额和企业避税频率的蒙特卡洛模拟结果具有较高的可信度。

1 数理推导

1.1 总体分位数求解

借鉴逆威布尔模型（2016）本文假设企业的生命周期为t年，用m表示企业的避税金额，n表示企业避税行为的频率，并且m和n均大于零，我们可以用以下公式表示企业避税行为的分布函数G和密度函数g：

对k个企业的避税行为周期进行分析，且满足以下初始条件：

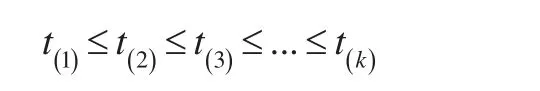
由于主客观等方面的原因，可能无法得知某些企业的具体避税行为，即所获得的数据可能存在缺失情况，当数据缺失时剩余L个企业的避税行为周期为：

为了使用逆威布尔模型，对企业避税行为周期取自然对数得：

则X的分布函数F和密度函数f变为：

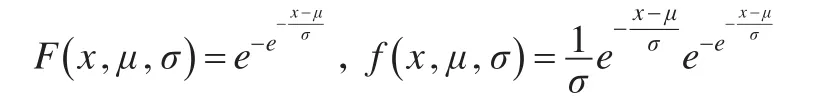
其中，Xi为企业避税行为周期的相应数据：

用正数p表示企业避税行为周期的样本分位数，满足以下公式：

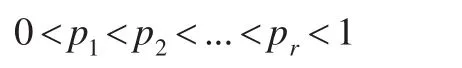
企业避税行为周期的总体分位数为q：

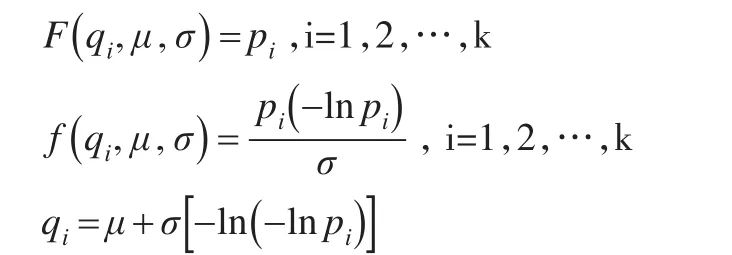
1.2 周期参数估计值

接下来利用上述企业避税行为周期的分位数构建计量模型，通过求解证明参数的渐近无偏性，当企业数量n趋向于无穷大时，可得：

根据上述公式构建如下计量模型：

基于最小二乘法对上述计量模型的参数进行求解可得参数的估计值：

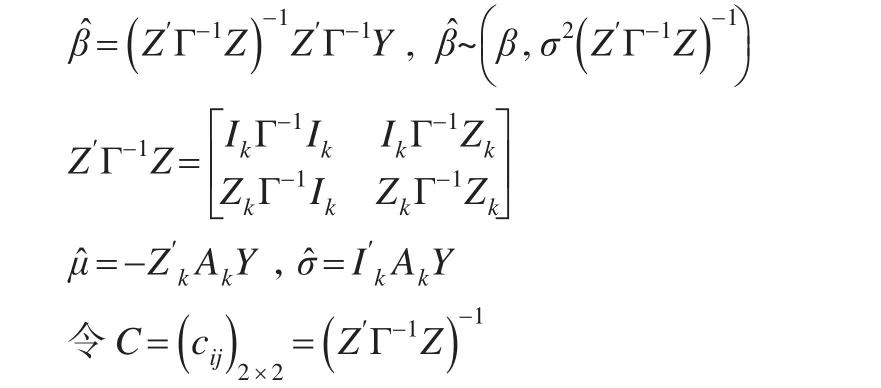
所以上述参数估计值的形式可以表述为：

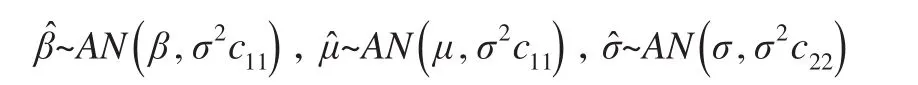
即得到的企业避税行为周期参数估计值是渐近无偏的估计值。

1.3 参数置信区间测度

为了进一步分析参数的精确度，对参数的置信区间进行测度，当置信水平为α时，假设企业避税行为周期分位数N属于正态分布，则σ的置信区间形式为：

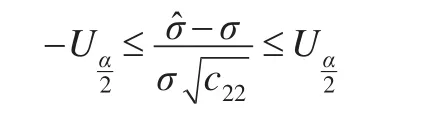
对上述公式求解可得σ的置信区间为：，根据前面假设σ=，因此可得

参数m的置信区间：

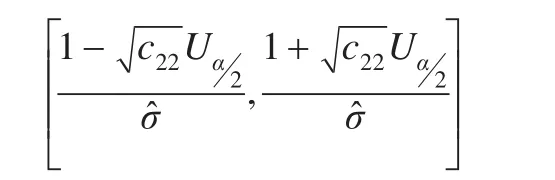
以表述为：

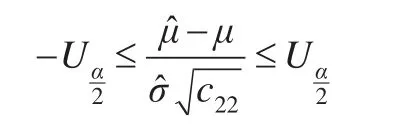
根据上述公式可得μ的置信区间形式为：

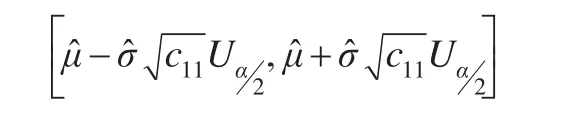
因为μ=lnq，可得q的置信区间为：

至此，对随机数据缺失条件下企业避税行为周期通过数理推导完成参数的渐近估计，并对参数的置信区间进行了测度，接下来利用上述模型使用统计数据对企业避税行为周期进行蒙特卡洛模拟研究。

2 模拟检验

2.1 β的模拟结果

为了检验模拟结果是否和随机数据缺失数量有关，随机数据缺失选择为20和40个；为了分析模拟结果是否和企业避税金额大小有关，企业避税金额分别选择1和10个标准单位；为了检验模拟结果是否和企业避税频率有关，企业避税频率分别选择5和50个标准单位。β的模拟结果见表1和图1。从模拟结果来看，当企业避税金额为1和10个标准单位时，蒙特卡洛模拟平均值分别为1.0482和10.1846，标准差分别为0.0461和1.0748，均方误差分别为0.0027和0.0534，模拟值的平均值在置信区间范围内，而且标准差和均方误差比较小，表示逆威布尔模型对企业避税金额的蒙特卡洛模拟结果具有较高的可信度。从逆威布尔模型对企业避税频率的蒙特卡洛模拟结果来看，当企业避税频率分别为5和50时，模拟结果分别为4.9837和50.3124，标准差分别为0.5372和5.3276，均方误差分别为0.0036和0.0849，模拟结果处于相应置信区间内，表示逆威布尔模型对企业避税频率的蒙特卡洛模拟也具有较高的可信度。即逆威布尔模型对企业避税行为周期的蒙特卡洛模拟认为相关系数β是无偏的，且模拟结果不随随机样本数据缺失数目的变化而变化。

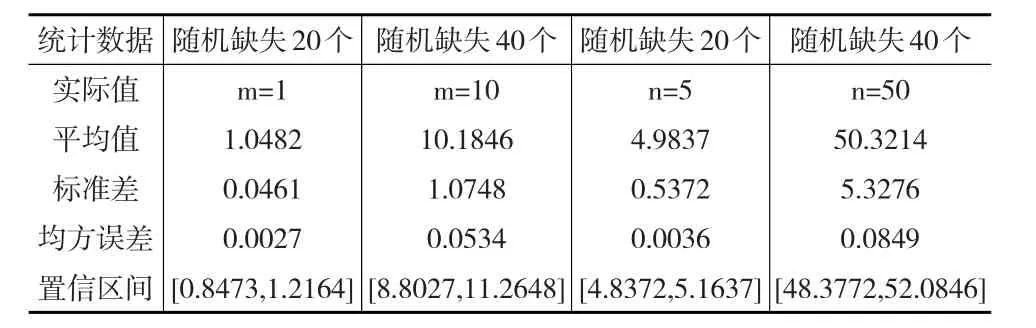
表1 β的蒙特卡洛模拟结果

图1 β的800次蒙特卡洛模拟结果和实际值

2.2 μ的模拟结果

接下来对参数μ进行蒙特卡洛模拟（见表2和图2），这里和参数β的模拟方法相似，数据缺失数量分为20和40两种情况，企业避税金额分别为1和10个标准单位，蒙特卡洛模拟的平均值分别为1.0524和10.0947，标准差分别为0.0593和1.0748，均方误差分别为0.0044和0.0534，且模拟平均值在置信区间之内。从逆威布尔模型对企业避税频率的蒙特卡洛模拟结果来看，当企业避税频率分别为5和50时，模拟结果分别为4.9635和50.3521，标准差分别为0.5421和5.3411，均方误差分别为0.0072和0.0614，模拟平均值在置信区间之内。表示逆威布尔模型对企业避税行为周期μ的蒙特卡洛模拟结果均处于置信区间之内，可信度较高。

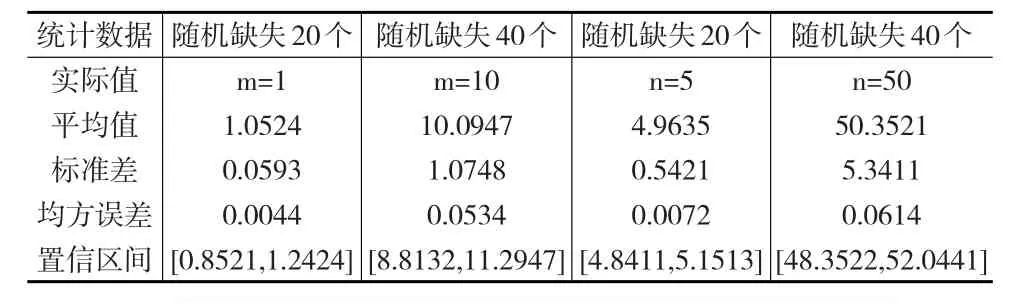
表2 μ的蒙特卡洛模拟结果

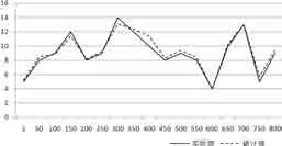
图2 μ的800次蒙特卡洛模拟结果和实际值

2.3 σ的模拟结果

基于逆威布尔模型对企业避税行为周期σ的蒙特卡洛模拟结果见表3和图3。表3和图3的模拟方法和表1与图1、表2与图2相同，依然分为数据随机缺失20个和40个。从模拟结果来看，当企业避税金额为1和10个标准单位时，蒙特卡洛模拟平均值分别为1.0938和10.1903；标准差分别为0.0331和1.0524，均方误差分别为0.0088和0.0590；模拟值的平均值在置信区间范围内，而且标准差和均方误差比较小，表示逆威布尔模型对企业避税金额的蒙特卡洛模拟结果具有较高的可信度。从逆威布尔模型对企业避税频率的蒙特卡洛模拟结果来看，当企业避税频率分别为5和50时，模拟结果分别为4.9635和50.3940；标准差分别为0.5562和5.3614，均方误差分别为0.0062和0.0872，模拟结果处于相应置信区间内，表示逆威布尔模型对企业避税频率的蒙特卡洛模拟也具有较高的可信度。即逆威布尔模型对企业避税行为周期的蒙特卡洛模拟认为相关系数σ是无偏的，且模拟结果不随随机样本数据缺失数目的变化而变化。

表3 σ的蒙特卡洛模拟结果

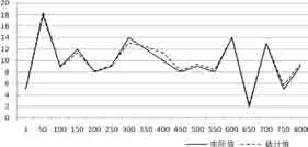
图3 σ的800次蒙特卡洛模拟结果和实际值

3 实证结果

上文借助逆威布尔模型对我国企业避税行为周期进行数理推导，并进行蒙特卡洛模拟，模拟结果验证了所构建模型的可信度。接下来使用我国上市公司2000—2016年的统计数据进行实证检验，原始数据来源于2000—2016年《中国上市公司统计年报》，共搜集了1000家上市公司数据，其中年营业额5000万元以上的大企业500家。年营业额5000万元以下的中小企业500家，由于某些企业的统计数据不完整，应该获取数据17000个，实际获取13000个，数据缺失率23.53%。由于存在数据的大量缺失，使用传统回归方法将会导致估计结果的偏颇，这里使用本文构建的逆威布尔模型对数据情况下的企业避税行为进行实证研究，分别对企业的避税金额、避税频率和避税行为进行检验，检验结果见表4。从检验结果可以看出，拟合系数在0.95左右表示实证结果的拟合性较好，相关系数β均通过了显著性检验且显著为正，表示我国企业缺失存在很明显的企业避税行为，其中营业额5000万以上的大企业和5000万以下的中小企业的避税行为存在较大不同，大企业的避税金额较大但避税频率较小，中小企业的避税金额较小而避税频率较高，从总体避税行为来看中小企业的避税行为较为明显，0.6424显著大于0.4837。

表4 企业避税行为实证检验结果

为了对我国企业避税行为的年度发展趋势进行研究，本文计算出大企业和中小企业2000—2016年避税行为的相关系数（见下页图4）。从图4可以看出2000年营业额高于5000万的大企业避税行为要高于营业额低于5000万的中小企业，但无论是大企业还是中小企业在2000年之后，避税行为都在逐年增加；大企业在2010年出现避税行为下降现象，中小企业在2011年左右出现下降现象，表示随着我国社会主义市场经济体制的逐渐健全和完善，企业越来越遵循市场经济规律，避税现象呈逐年下降趋势；目前来看中小企业的避税行为要大于大企业。

图4 2000—2016年企业避税行为发展趋势

4 结束语

本文借鉴逆威布尔模型的基本思想，对企业避税行为周期进行数理推导，研究在数据缺失情况下逆威布尔模型对企业避税金额和避税频率估计参数的渐进一致性，并推导出参数的置信区间。利用逆威布尔模型对企业避税行为周期进行蒙特卡洛模拟800次，为了检验模拟结果是否和随机数据缺失数量有关，随机数据缺失选择为20和40个；为了分析模拟结果是否和企业避税金额大小有关，企业避税金额分别选择1和10个标准单位；为了检验模拟结果是否和企业避税频率有关，企业避税频率分别选择5和50个标准单位。各参数的模拟结果表明，相应模拟结果均处于置信区间内，且模拟结果不随随机样本数据缺失数目的变化而变化，也不因企业避税金额和企业避税频率的变化出现不一致情况。本文所构建的逆威布尔模型对企业避税行为周期的估计是渐进无偏的一致估计量，企业避税金额和企业避税频率的蒙特卡洛模拟结果具有较高的可信度，在现实生活中我们使用该模型对企业避税行为周期进行数理推导和实证研究。实证结果显示，样本分析期的初期大企业的避税行为高于中小企业，由于我国社会主义市场经济体制的逐步健全和完善，所有企业的避税行为在经历逐年递增阶段后开始出现下降，目前来看中小企业的避税行为要高于大型企业。

参考文献：

[1] Nye L S.The Effect of Finance Risk CPI in the city Analsis of Cargo Hanling Operations[J].Physica-VerlagHD,2013,(4).

[2] Weber P.Theory of the Travel Industry Location of city[M].Chicago:The University of ChicagoPress,2015.

[3] Wardman H.Interurban Travel Demand Elasticity and Employment Risk Competition in Great Britain:Evidence from Direct Demand Mod⁃els of City[J].Transportation Research,2013,5(4).

[4] Jieur K.Interurban Travel Demand Elasticity and Employ Riskness Competition in Great Biueyr:Evidence From Direct Demand Models city Eco-tourism[J].Transportation Research,2014,(6).

[5] Geyrre D A.Is Employment Travel Risk Expenditure Productive?[J].Journal of Monetary Economics,2015,（23）.

[6] Kiuejnr E M.The Location of Travel in Economic Activity of inflation.[M].New York:Mc Graw-Hill,2010,（4）.

[7] 林毅夫，赵阳，赵磊.企业避税行为对国民经济运行的危害性分析[J].经济研究,2017,(4).

[8] 唐宜红，刘海兵.企业避税行为周期的影响因素研究——基于避税应对危机的政策选择[J].数量经济技术经济研究,2016,(12).

[9] 郑世林.企业避税行为的纠正:新一轮消费结构升级的重要引擎[J].世界经济，2016,(5).

[10] 卢嘉瑞.消费智能化:新一轮消费结构升级的重要引擎[J].管理学刊，2016,(5).

[11] 谢孟军，汪同三，崔日明.中国的文化输出能推动对外直接投资吗？——基于孔子学院发展的实证检验[J].经济学（季刊），2017，16(4).