四种自相关模式控制图的比较研究

孙小素

（山东工商学院 统计系，山东 烟台 264005）

0 引言

统计过程控制技术（SPC）对于监控过程的稳定性，提升产品品质发挥了巨大的作用。传统的SPC控制图假设观测值相互独立，但在实际应用中，制造过程往往具有自相关性，若将此类型资料以传统的常规控制图进行监控，容易产生误判，从而导致不必要的成本浪费。因此，有部分学者[1]，提出配适原始资料的时间序列模型，由于假设模型的残差彼此独立，若模式配适正确，即可利用传统的SPC控制图监控残差值，达到监控品质的目的。目前已有4种控制图适合侦测自相关过程均值的变动，分别是残差EWMA控制图、残差CUSUM控制图、Autoregressive T2控制图以及ARMA控制图。Lu和Reynolds（2001）[2]指出在监控自相关制造过程上，残差EWMA控制图与残差CUSUM控制图的表现十分相似。Apley和Tsung（2002）[3]认为Autoregressive T2控制图的侦测效果较残差CUSUM控制图佳。Jiang（2000）[4]等认为ARMA控制图较EWMAST控制图佳。张志雷（2012）[5]对ARMA和残差控制图进行了比较研究，认为ARMA更为灵敏。从这些学者的研究内容看，目前尚无对4种自相关控制图的整体性评估。正是由于4者缺乏整体性评估，质量管理人员在面对自相关制造过程时，对于应该采用何种控制图进行监控更为合理常感困惑。本文将针对这4种控制图在监控自相关过程上的表现做详尽的比较分析，并针对这4种控制图的使用时机进行评估并提出建议，为质量管理人员的正确选择提供理论依据。

1 四种自相关模式控制图述评

传统的SPC控制图假设所有观测值相互独立，但如果将具有显著自相关性的过程视为独立时，很容易因低估过程变异使控制界限比实际来得狭窄，而造成过高的误警率与频繁的调整。因此，探讨自相关过程的监控方法非常必要和重要。近年来，在众多学者[6,7]的努力下，已开发出两类适用于监控自相关过程的控制图：其一是先拟合自相关过程的时间序列模型，再利用时间序列模型残差相互独立且服从正态分布的特性，以传统控制图直接监控残差值，即可达到及时侦测异常模式的目的。其二是使用传统的常规控制图，但必须重新调整常规控制图的上下控制界限，因为具有自相关性的过程其变异通常会增大。

1.1 EWMA残差控制图

Montgomery和Mastrangelo（1991）指出过去的学者针对自相关过程的监控准则均先将原始资料拟合时间序列模型，再利用常规控制图对残差进行监控，但若过程均值变动量较小，传统的常规控制图不易侦测其异常点，故他使用EWMA控制图代替常规控制图。

Wardell等（1994）则利用模拟的方式分别比较当过程为ARMA(1,1)模式时，传统的常规控制图、EWMA控制图、有额外控制界限预测值常规控制图与残差值常规控制图的侦测效果。

Harris和Ross（1991）[8]深入探讨数个不同相关性结构的过程，如AR(1)模式、含非相关误差的AR(1)模式（AR（1））、有自相关误差的固定量测等对传统EWMA控制图与CUSUM控制图多造成的影响，结果发现当自相关程度很高时，无论是使用哪一种控制图对于监控过程均值微小偏移的效果均非常不理想，容易产生误判。

Zhang（1998）考虑不使用残差值进行监控，而将原始的EWMA控制图中侦测统计量的标准差估计式，转换成以自相关函数（Autocorrelation Function，简称ACF）的函数形式表示，重新修正原始EWMA控制图的控制界限，使修正后的EWMA控制图较稳健而不容易受过程的自相关性所影响，他将其称为EWMAST控制图。

Lu和Reynolds（1999）[9]构造了过程为ARMA(1，1)模式的残差EWMA控制图。他们分别评估以原始观测值为基础以及以残差为基础的EWMA控制图在面对不同自相关程度过程上的表现，发现在监控低度或中度的自相关过程时，两者的表现非常接近；但针对高相关过程时，残差值EWMA控制图在侦测过程均值偏移时的速度较快。

1.2 CUSUM残差控制图

Runger等（1995）利用马尔科夫链方法推导出AR(1)模型残差值的CUSUM控制图的平均链长计算公式。他们认为，若过程为AR(1)模式，当过程均值发生偏移时，残差值的期望值将不再是一个固定的常数，因此建议将参考值设定为(1-ϕ)σ2。

Lu和Reynolds（2001）[2]构造出以残差值为基础的双侧CUSUM控制图，他们对该控制图在监控自相关过程的侦测效果进行了评估，得到了与他们在1999年关于残差EWMA控制图相类似的结果，即原始观测值与残差值的CUSUM控制图在低中度相关程度上的侦测效果十分相近，在高度自相关时残差值CUSUM控制图的表现为佳。

1.3 AutoregressiveT2控制图

Apley和Tsung（2002）[3]采取一种不同于前面所述的方法监控自相关过程，他们延续了Krieger（1992）[10]等及AlwanA.J和AlwanL.C（1994）[6]的想法，将原始过程的单变量观测值以视窗方式分割成多变量，并仿照HotellingT2控制图的监控方法，提出AutoregressiveT2控制图。他们令xt为自相关过程在t时刻的观测值，假设过程服从正态分布，其均值为μ，自协方差为γk=E[(xt-μ)(xt+k-μ)]。记μ0是已知的目标值。以视窗大小p切割原始观测值得到一个p维向量Xt={xt-p+1，xt-p+2，…，，则Xt服从p维正态分布。若xt为一稳定的ARMA模式，记Xt的协方差矩阵为∑，当过程受控是均值向量为μ0={μ0，μ0，…，，若 ∑已知，则控制统计量就服从自由度为p的卡方分布，在固定的α下，其控制的上限为(p)。

1.4 ARMA控制图

特殊原因控制图SCC（Special-Cause Chart）与EWMAST控制图设计的初衷是，以原始观测值为控制统计量，通过调整常规控制图的控制界限，来消除自相关的影响。但如果仔细比较这两种控制图的侦测效果，不难发现若实际过程表现为ARMA(3，2)，EWMAST侦测过程微小变动的速度较SCC快；当过程为ARMA(2，1)时，SCC的表现又优于EWMAST。可见，这两种控制图的表现会因过程的不同自相关模式而不同。因此，质量管理人员面对不同的过程自相关模式时就存在控制图的选择问题。否则一旦使用错误，会延缓侦测出偏移的最佳时机或产生较高的误警率。故Jiang等（2000）[4]建议使用一种新的控制图——ARMA控制图来取代SCC与EWMAST控制图。

假设过程为一稳定状态的ARMA模式，依据Zhang（1998）构造EWMAST控制图的方法，则ARMA控制图统计量Zt可通过下式计算：

而稳定状态Zt的方差为：

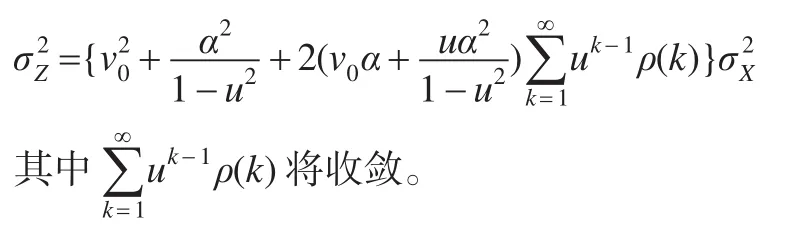
当u=1-λ，v=0时，ARMA控制图即为EWMAST控制图，而当u=θ，v v0=ϕ时，ARMA控制图即为SCC控制图，故EWMAST控制图与SCC控制图可视为ARMA控制图的特例。可见，ARMA控制图适用面更广，侦测均值变动的范围较大，且侦测效果也好于前两种控制图。

2 四种自相关过程控制图的比较

2.1 控制图侦测效果评价标准的设定

衡量控制图侦测效果的指标有很多，如漂移敏感性、误警率、平均链长等，本文选择控制图最常用的评估指标——平均链长（简称ARL），以衡量控制图的控制效果。平均链长依据过程是否处于受控状态，可分为受控状态的平均链长（记为ARL0）以及失控状态下的平均链长（out-of-control ARL，记为ARL1），前者是指当过程处于稳定状态时，从开始到控制图发出异常警报所需的样本数；后者是指当过程失控时，从开始到侦测出失控所需的样本数。一般而言，若过程失控，平均链长越小，说明失控状态被侦测出来的速度越快。因此，本文在对各控制图进行比较研究时，假设所有控制图在受控状态时的平均链长为370，同时设定不同的漂移量（δ=(μ1-μ0)σ），观察其脱离受控状态时的平均链长ARL1。

2.2 不同自相关程度及不同时间序列模型对控制图侦测能力的影响

本文设定5种漂移量——δ=0.25，0.5，1，2，3，每次只有一个观测值（即n=1），在低度、中低度、中度及高度相关程度下，以失控状态下的平均链长并参考Lu和Reynolds（1999）[9]所提及的AR(1)及随机误差模式的作法，来评估残差EWMA、残差CUSUM、Autoregressive T2、ARMA这4种控制图监控过程均值变动的能力。

2.2.1 AR(1)及随机误差模式

若将自相关过程的观测值Xk记为：Xk=μk+εk，式中，μk为时刻k过程的均值；εk为一独立且服从正态分布，均值为0，方差为的随机变量。假设，μk为一AR(1)模式的过程，其均值为ς，则：

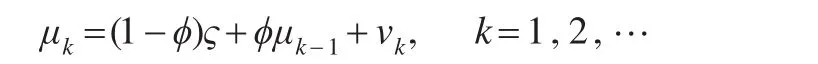
其中，vk为AR(1)模式的随机误差；ϕ为自回归参数，满足 |ϕ|≤1。

若vk~N(0，为一独立的正态随机变量，且vk与εk不 相 关 ，则=(1-ϕ2)。 因 此 ，E(Xk)=ς，Var(Xk)==+。定义ψ==(+，表示AR(1)模式变异占整个过程变异的比例，亦即AR(1)模式影响整体过程的程度。同时，由前面的关系式不难求出，观测值Xk-1与Xk之间的自相关系数为ρ=ϕψ。

2.2.2 ARMA(1，1)模式

若原始过程为ARMA(1，1)模式，则观测值Xk可由下面的关系式表示：

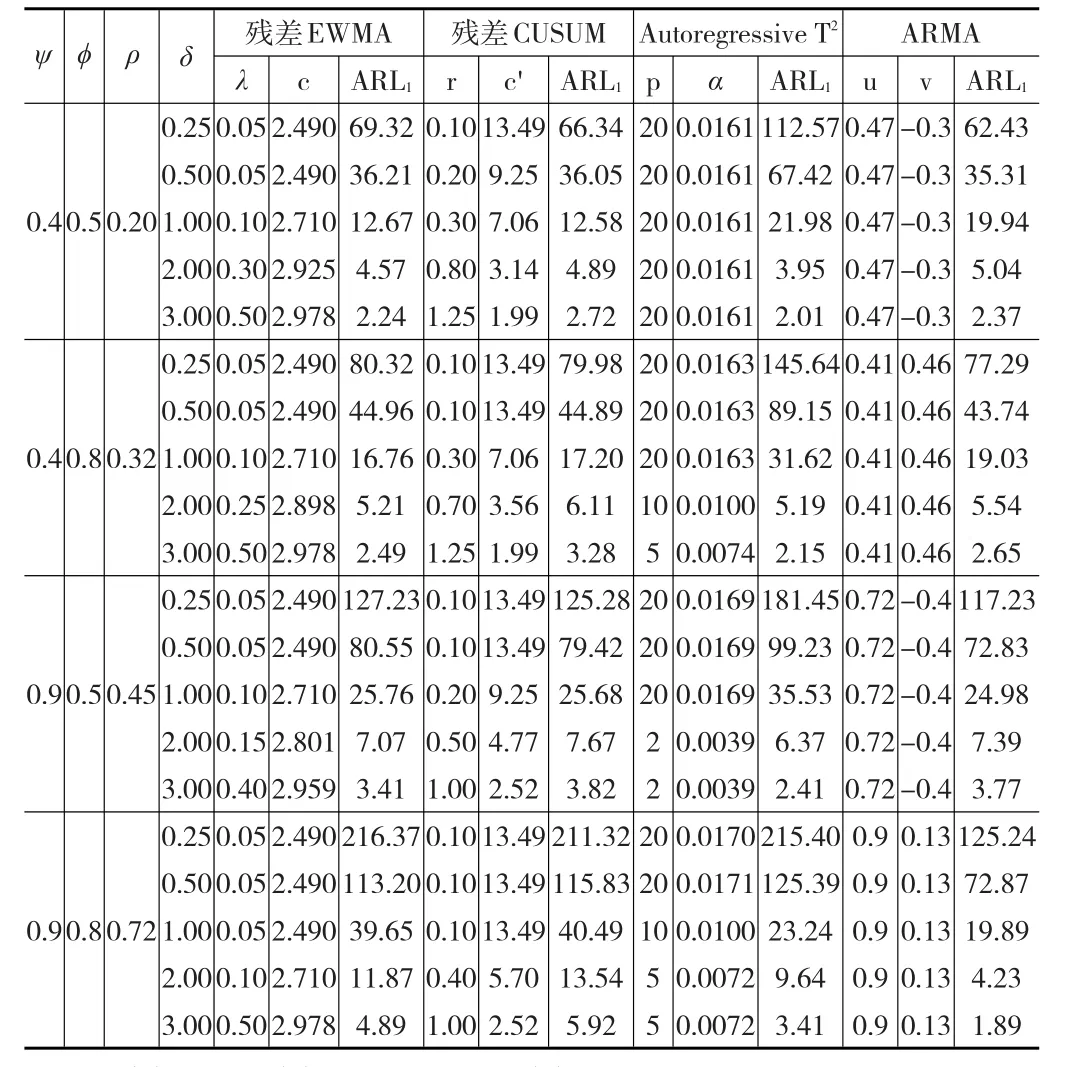
表1 不同自相关程度下，4种控制图的ARL1

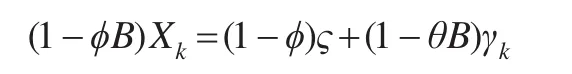
其中，γk为独立的正态随机变量，其均值为0，方差为。θ为移动平均参数，ϕ为自回归参数。

Reynolds等（1996）曾推导出一参数转换公式，可将ARMA(1，1)模式的参数ϕ、θ、以AR(1)加随机误差模式的参数ϕ、σv2、来表示。

若ϕ＞0，即观测值为正自相关，则：

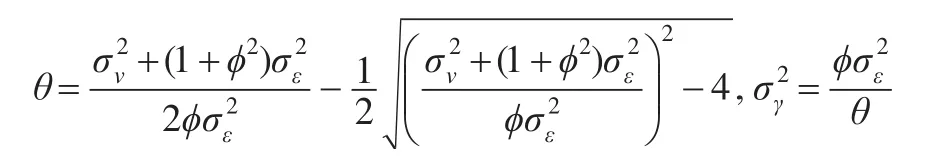
反之，亦可将AR(1)加随机误差模式以ARMA(1，1)模式的参数表示。若ϕ＞0，即观测值为正自相关，则相应的表达式为：

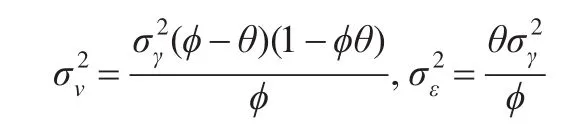
2.2.3 不同自相关程度对控制图侦测能力的影响

假设ς=0，=1.0，=0.5，并考虑自回归参数为正数（这一假定比较合理，因为很多过程自相关的原因均为惯性的作用），在不同的自相关程度下，用前面介绍的4种控制图模拟10000次，计算其失控状态下的平均链长ARL1，整理列入表1中。模拟过程需要说明的是：（1）EWMA残差控制图采用的是Lu和Reynolds（1999）[9]所提及的AR(1)及随机误差模式的作法，该图的控制上下界线为（因为假定ς=0），其中λ为平滑系数，c为与第一类错误α相关的概率度，如α=0.27%时，c=3；（2）CUSUM残差控制图使用的统计量由Lu和Reynolds（2001）[2]定义为：

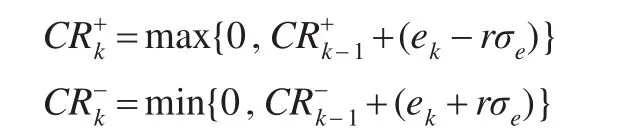
其中，rσ为参考值，若或超出控制界限±c'σ，则控制图将发出警报；（3）Alwan A.J和 Alwan L.C（1994）[6]指出，质量管理人员要使用Autoregressive T2控制图，必须先设定视窗大小p及第一类错误的概率α；（4）关于u，v，则采用Zhang（1998）利用自相关函数（ACF）重新修订原始EWMA控制图，构建ARMA控制图中的参数；（5）4种控制图中的参数的确定方法是，不断试算以确保ARL0约为370。

表1列出的模拟结果表明，在低度自相关(ρ=0.2)，过程均值漂移量较小时(0.25σ,0.5σ)，控制效果最好的控制图为ARMA控制图；在相同的相关程度下，当漂移量达到1.0σ时，则以CUSUM残差控制图为最佳；当漂移量进一步增大，超过1.0σ时，则以Autoregressive T2控制图侦测效果最佳。增加自相关程度，达到低中度相关的0.32，在过程均值较小的漂移量(0.25σ,0.5σ)，仍以ARMA控制图效果最佳；漂移量达到1.0σ时，则以EWMA残差控制图为最佳；当漂移量超过1.0σ时，则以Autoregressive T2控制图侦测变动的速度最快。在中度自相关(ρ=0.45)时，过程偏移量为0.25σ，0.5σ及1.0σ时，侦测效果最好的控制图均为ARMA控制图；超过1.0σ时，则以Autoregressive T2表现最佳。在高度自相关(ρ=0.72)时，在任何漂移量下均以ARMA控制图的侦测效果最佳。

综合上面的分析，不难得到如下的结论：

其一，随着过程的自相关程度增加，资料彼此干扰的现象将变得严重。因此，不论是应用何种控制图，在过程均值发生同等漂移时，都需要更长时间才能侦测到（见各种控制图同一列的ARL1）；

其二，总体来看，以残差为基础设计出的两种控制图——CUSUM与EWMA，其侦测效果十分接近，但在侦测较小偏移量(低于1.0σ)时，以CUSUM残差控制图略佳；而对于大的偏移量(超过2.0σ)，又以EWMA残差控制图略佳；

其三，如同Apley和Tsung（2002）[3]模拟结果显示的那样，Autoregressive T2控制图在侦测大型偏移时(不低于2.0σ)较残差的两种控制图来得迅速，在侦测小的偏移量(低于2.0σ)时，又不如残差的两种控制图。本文认为其中的原因是Autoregressive T2控制图将单变量观测值以视窗方式转换成多变量，在转换的过程中容易丢失过程均值微小偏移的信息。此外，Apley和Tsung两位学者仿照Hotelling T2控制图建立控制图，Hotelling T2控制图本身就对侦测过程的微小变动不灵敏；

其四，在过程低度或中度自相关时，EWMA残差控制图在侦测较大的偏移时(不低于1.0σ)胜于ARMA控制图，但差距并不明显。总体来看，ARMA控制图的监测效果较不易受过程自相关程度的大小所干扰，因此，最适合用于高度自相关过程的异常模式侦测。

综上所述，对具有自相关过程的统计控制，可首选ARMA控制图来侦测其异常模式。

2.2.4 不同时间序列模型对控制图侦测能力的影响

表1比较了不同自相关程度下，4种控制图侦测异常模式的效果，并未区分自相关的时间序列模型。事实上，时间序列可以构建不同的模型，模型不同又会对4种控制图的侦测效果造成什么影响？

这里假设ς=0，=1.0，亦仅考虑正自相关的情形。同样使用模拟的方法，计算4种控制图的ARL1，联同设定的相关参数一并列入表2。

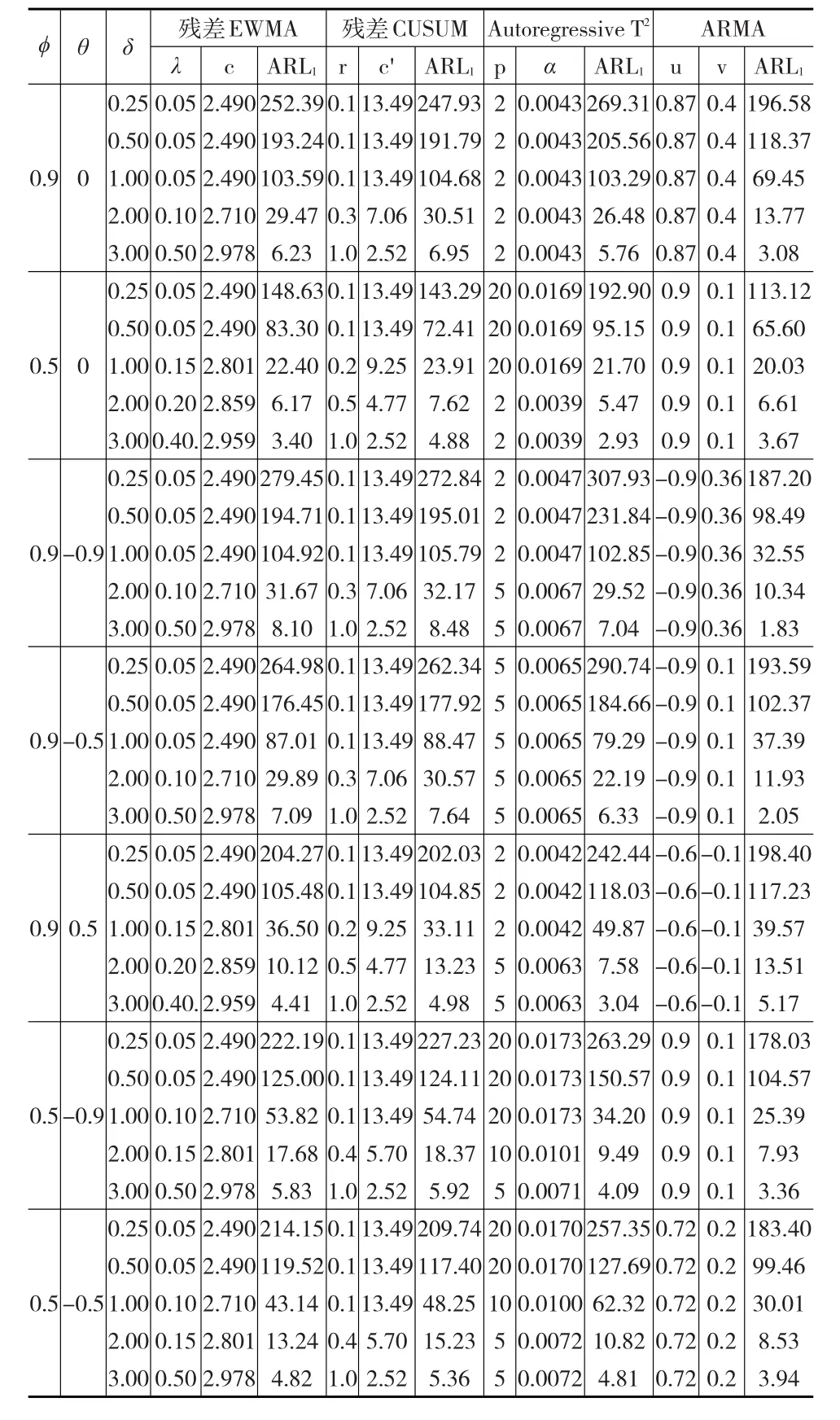
表2 不同时间序列模型下，4种控制图的ARL1

观察表2可知，在过程为AR(1)模式下，当ϕ=0.9时，无论均值偏移大小，ARMA控制图远好于其他3种。当ϕ=0.5时，均值偏移量较小时(不超过1.0σ)，依然是ARMA控制图远好于其他3种；均值偏移量较大时(超过1.0σ)，Autoregressive T2控制图侦测异动最快，但不比ARMA快太多。在过程为ARMA(1,1)模式下，当ϕ=0.9，θ=-0.9或ϕ=0.9，θ=-0.5时，同样无论均值偏移大小，ARMA控制图远好于其他3种。在ϕ=0.9，θ=0.5下，均值小的偏移(0.25σ)，还是ARMA控制图最好；但均值偏移量大(超过1.0σ)后，最灵敏的控制图就变为Autoregressive T2控制图。在ϕ=0.5，θ=-0.9或ϕ=0.5，θ=-0.5时，同样无论均值偏移大小，4种控制图的监测效果以ARMA控制图为最佳。

3 结论

本文通过上面分析和比较，可以得到下述结论：

其一，若过程为AR(1)模式，则自回归系数ϕ越大，任何自相关控制图侦测出异常所需的时间越久，相比较而言，ARMA控制图好于其他3种控制图。

其二，若过程为ARMA(1,1)模式，给定自回归系数ϕ，当移动平均系数θ越小时，则ARMA控制图的ARL1越小，但其他3种控制图却越大。若给定移动平均系数θ，自回归系数ϕ越小时，4种控制图的ARL1均越小。

其三，整体而言，除了在低、中度自相关下，ARMA控制图侦测过程均值大偏移的速度较EWMA残差控制图稍慢外，4种控制图以ARMA控制图的侦测效果为最佳。

综合前文的分析，对具有自相关过程（不管自相关程度如何）的统计控制，无论自相关的过程是AR(1)模式，还是ARMA(1,1)模式，可首选ARMA控制图来侦测其异常模式，但做控制图之前应先确立时间序列模型，因为模型不同ARMA控制图的侦测效果差异很大。

参考文献：

[1] Alwan L C,Roberts H V.Time-Series Modeling for Statistical Pro⁃cess Control[J].Journal of Business and Economic Statistics,1998,(6).

[2] Lu C W,Reynolds M R.CUSUM Charts for Monitoring An Autocorre⁃lated Processes[J].Journal of Quality Technology,2001,(33).

[3] Apley D W,Tsung F.The Autoregressive T2 Chart for Monitoring Uni⁃variate Autocorrelated Processes[J].Journal of Quality Technology,2002,(34).

[4] Jiang W,Tsui K L,Woodall W H.A New SPC Monitoring Method:The ARMA Chart[J].Technometrics,2000,(42).

[5] 张志雷.自相关过程的ARMA控制图[J].统计与决策，2012，（6）.

[6] Alwan A J,Alwan L C.Monitoring Autocorrelated Processes Using Multivariate Quality Control Charts[C].Proceedings of the Decision Sciences Institute Annual Meeting,1994,(3).

[7] Adams B M,Tseng L T.Robustness of Forecast-Based Monitoring Schemes[J].Journal of Quality Technology,1998,(30).

[8] Harris T J,Ross W H.Statistical Process Control Procedure for Corre⁃lated Observations[J].Canadian Journal of Chemical Engineering,1991,(69).

[9] Krieger C A,Champ C W,Alwan L C.Monitoring an Autoregressive Process[C].Presented at the Pittsburgh Conference on Modeling and Simulation,Pittsburgh,PA,1992.

[10] Krieger C A,Champ C W,Alwan L C.Monitoring an Autoregressive Process[C].Presented at the Pittsburgh Conference on Modeling and Simulation,Pittsburgh,PA,1992.