基于误差修正项调整的高阶单整变量差分建模
2018-05-22白鹤松曲振涛
白鹤松,曲振涛
(哈尔滨商业大学 经济学院,哈尔滨150028)
0 引言
传统Granger检验方法的适用要求所有检验的变量必须是平稳的或者是趋势平稳的,如果出现不平稳现象则无法对高阶单整变量的因果相关性做出准确判断。但是现实生活中往往出现变量的单整现象,此时传统检验方法失效。为此,本文推介一种用于检验高阶单整变量因果关系的研究方法,试图从同阶变量和不同阶变量两个方面进行拓展研究。
1 均方误差最小化的传统Granger检验及其适用条件
目前学界使用的Granger因果检验主要是基于均方误差的最小化而进行,假设变量在第t期的数据集为Jt,要想检验变量X预测值的准确性,只需满足改变量的均方误差最小,均方误差(MSE)的公式表达方式为:

此时可以通过求解X的条件均值来确定MSE的最小值,数据集Jt条件下的条件均值可以表述为:

当下述公式成立时认为Granger因果关系不成立,因为变量Y的消除不会改变X的均值;反之,当下述公式不成立时即变量Y的消除会改变X的均值,则可以认为存在Granger因果关系:
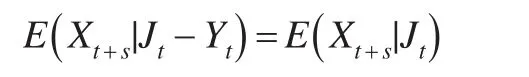
如果变量X为线性函数形式,可以使用变量X的投影来检验,检验公式为:
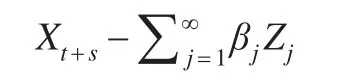
其中为变量X的线性投影,当变量X的预测值与投影值之差和Zh不存在相关关系时,则Y和X之间具有Granger因果关系,即满足:
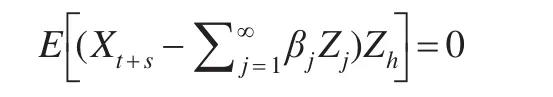
如果用VAR模型检验变量之间的因果关系,则可以表述为如下联合方程式:
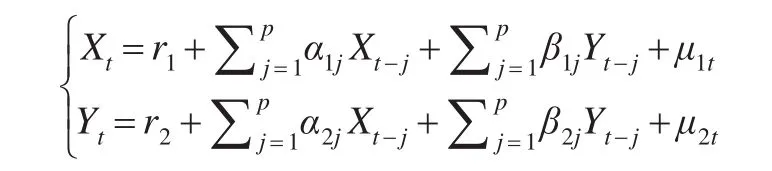
其中μ表示随机扰动项,其均值为1,方差为常数,协方差为零,用公式表示为:
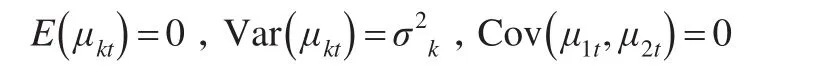
首先确定变量Y是X的因果关系,对于HY→X,如果满足β=0,则变量Y是X的因果关系不成立,如果满足β≠0,则变量Y是X的因果关系成立。此时一般使用F检验,统计量的表达方式为:
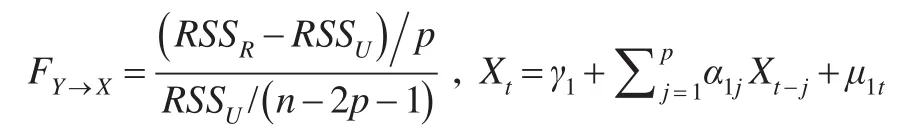
该公式服从F(p,n-2p-1)分布,通过查F分布表把其值与样本值比较确定显著性来判断因果关系是否成立。
然后确定变量X是Y的因果关系,对于HX→Y,如果满足β=0,则变量X是Y的因果关系不成立,如果满足β≠0,则变量X是Y的因果关系成立。此时一般使用F检验,统计量的表达方式为:
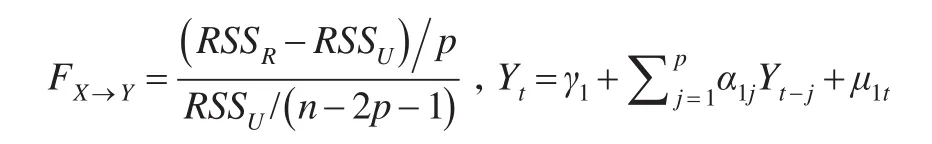
该公式服从F(p,n-2p-1)分布,通过查F分布表把其值与样本值比较确定显著性来判断因果关系是否成立。
使用这种方法进行Granger因果关系检验要求所有检验的变量必须是平稳的或者是趋势平稳,如果出现不平稳现象则无法检验。
2 同阶协整与不同阶协整检验及其建模
2.1 同阶协整变量因果关系检验
传统的Granger因果检验要求变量的平稳性,但是现实生活中往往出现变量的单整现象,此时传统检验方法失效,在出现高阶单整时可以对传统检验模型进行拓展,从而更好地进行因果关系检验:
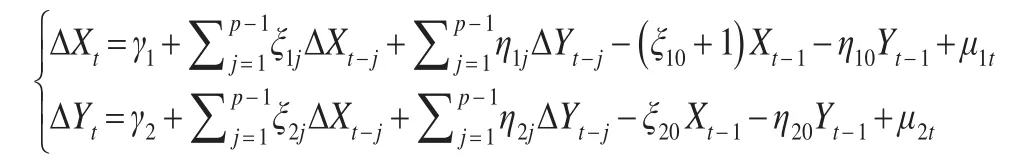
当X和Y具有2阶单整关系时,即满足如下公式:
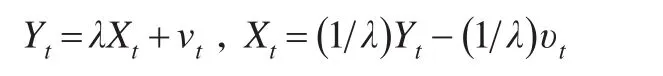
此时,上述检验模型可以等价转化为:
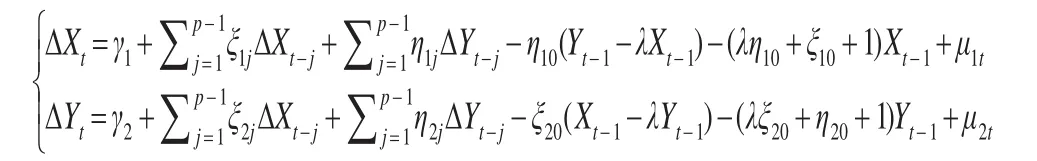
因上述公式为2阶单整模型,所以满足以下公式:
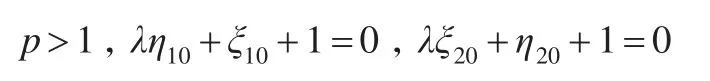
把上述条件带入模型,可得如下公式:
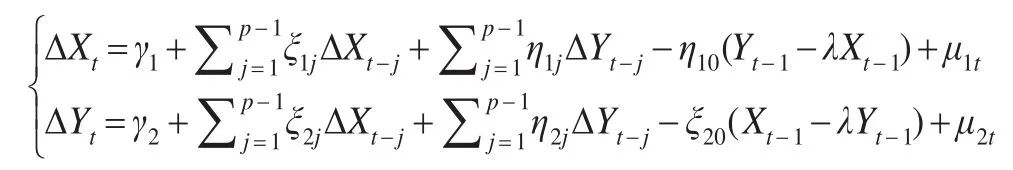
又因ΔX和ΔY两变量具有协整关系,可以推导出:
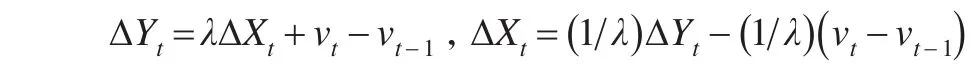
可以进一步把模型转化为如下形式:
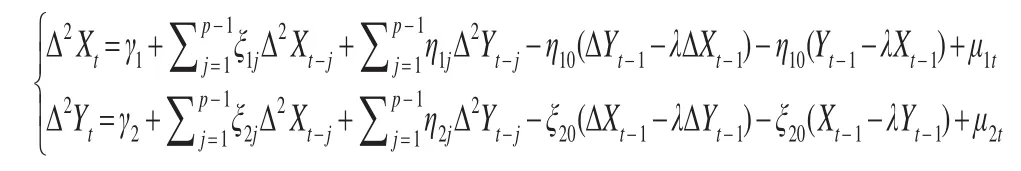
该模型是传统Granger检验模型的修正表达方式,主要通过误差修正项保证变量的平稳性,误差修正项的表达式为:Yt-i-λXt-i和Xt-i-1/λYt-i
如果误差修正项中的修正系数λ已知,可以通过F检验对变量之间的因果关系进行检验,当修正系数λ未知时可以使用以下公式计算修正系数,然后再通过F检验对变量之间的因果关系进行检验:
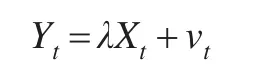
如果要检验的变量属于(d,d)型的高阶单证变量均可使用此方法进行因果关系检验。但是对于两变量不同阶的情况则不能使用此方法,下面对不同阶的协整模型因果关系的检验进行拓展研究。
2.2 不同阶协整变量模型检验
如果变量X和变量Y属于不同阶的协整关系,假设变量属于如下类型:
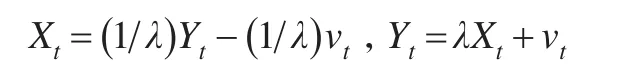
此时模型的形式可以转变为:
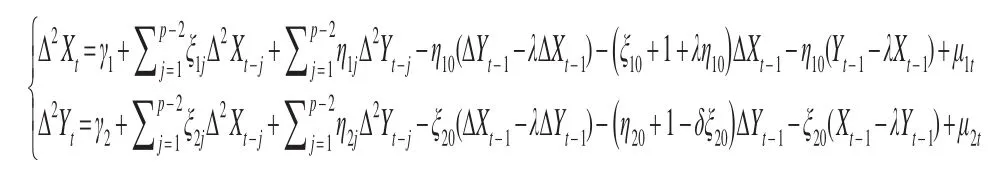
当上述模型中Yt-1-λXt-1和ΔXt-1或ΔYt-1属于协整关系时,可以构建如下误差修正模型进行因果关系检验:
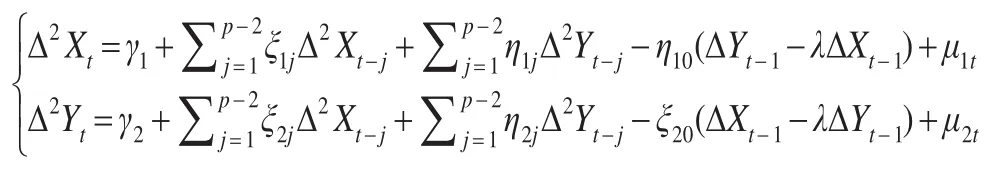
在Yt-1-λXt-1和 ΔXt-1或 ΔYt-1属于协整关系时,即满足以下公式:

把这种协整关系公式带入上述模型可得:
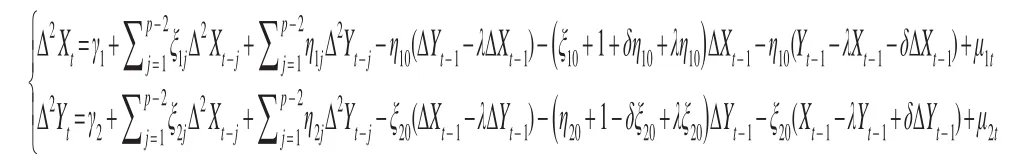
上述模型求解后可得:
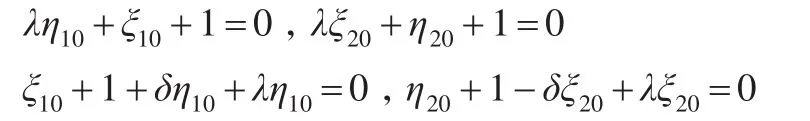
当λ和δ已知时可以把数值带入计算,并通过查F分布表以确定协整关系,如果λ和δ未知,则可以根据以下公式计算然后再检验协整关系:
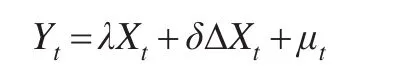
3 不存在协整关系的变量差分检验与建模
上文对具有协整关系的变量之间的Granger因果关系检验方法进行阐释,如果变量之间不存在协整关系则无法使用上述模型进行检验,接下来对这种情况进一步研究。假设X和Y都属于单整变量但不均有协整关系,当单整阶数相同时本文通过构建差分模型进行检验:
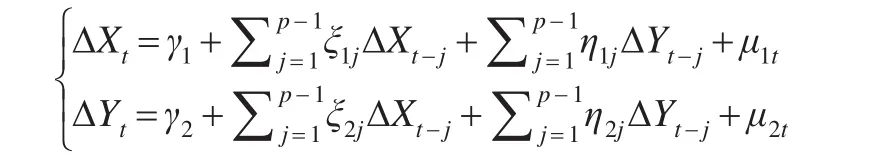
需要对以下差分形式进行因果关系检验:
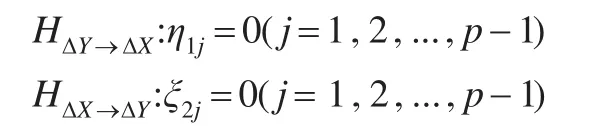
当上述差分检验公式成立时,变量X和Y不存在Granger因果关系,反之如果上述差分公式不成立则变量X和Y之间存在Granger因果关系。即可以通过检验差分形式ΔX和ΔY来确定变量X和Y的因果关系。
如果变量X和Y的单整阶数不同时,本文构建的检验模型如下:

当上述模型满足如下条件时可以进行因果关系检验:
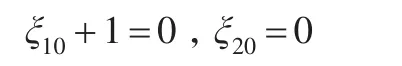
把上述条件带入检验模型可得:
通过这种方法可以解决高阶单整变量且变量之间阶数不同时的协整关系,因此本文推介的Granger因果检验方法对高阶(同阶和不同阶)的单整变量有很强的普适性。
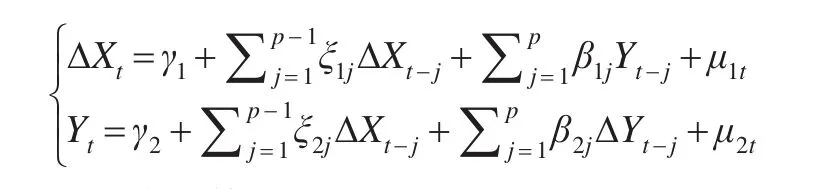
上述模型等价于以下d1-d2差分模型:
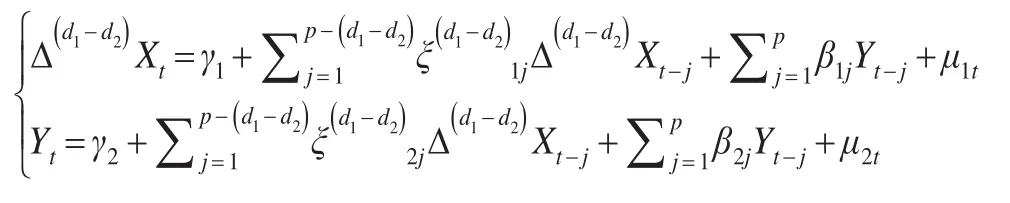
至此,本文把变量之间不存在协整关系的两种情况同阶单整变量和不同阶单证变量的Granger因果关系检验方法进行阐释。模型阶数的确定是因果关系进行检验的前提,所以要想对变量之间的因果关系进行检验需要首先选择变量的阶数。本文可以使用滞后参数值来确定模型阶数,当参数值最大时就是我们所要寻找的合理阶数,最大滞后值的求解方法是似然比,其公式表达形式为:
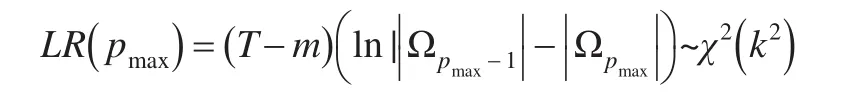
其中m表示需要估计的参数的个数,| Ω |表示待估计因果关系的矩阵行列式。在检验的过程中要保证模型中的误差项为随机扰动项,即变量不能存在自相关现象。这里使用多元LM自相关检验来确定是否存在自相关,对于n阶变量在显著性水平α下,当LM>χ2(k2)时表示变量存在自相关性,如果LM<χ2(k2)则表示变量不存在自相关,可以使用本文推介的方法进行检验。
4 结束语
针对传统Granger因果检验方法无法对互为因果的关系做出准确判断这一局限性,为了对高阶单整变量之间的Granger因果关系进行科学准确地判断,本文推介一种用于检验高阶单整变量因果关系的研究方法。文章首先对基于均方误差的最小化的传统Granger因果检验的基本思路进行数理推导,并指出该方法存在的检验劣势,即使用这种方法进行Granger因果关系检验要求所有检验的变量必须是平稳的或者是趋势平稳,如果出现不平稳现象则无法检验。但是现实生活中往往出现变量的单整现象,此时传统检验方法失效,在出现高阶单整时可以对传统检验模型进行拓展,从而更好地进行因果关系检验,从同阶变量和不同阶变量两个方面进行拓展研究。拓展研究对具有协整关系的变量之间的Granger因果关系检验方法进行阐释,但是如果变量之间不存在协整关系则无法使用上述拓展模型进行检验,接下来本文对不存在协整关系的变量之间的因果关系检验进行进一步研究。本文推介的高阶单整变量因果关系的检验方法具有普适应,可以推广到相关产业领域的实证检验。
参考文献:
[1] Nye S S.The Effect of Finance Risk CPI in the City Analsis of Cargo Hanling Operations[J].Physica-VerlagHD,2000,(4).
[2] Wardman H.Interurban Travel Demand Elasticity and Employment Risk Competition in Great Britain:Evidence From Direct Demand Models of City[J].Transportation Research,2013,5(4).
[3] Hoonoum M.Zhang A M,Zhang Y M.Optimal Demand for Travel Lease of City Eco-tourism[J].Transportation Research,2014,(6).
[4] Geyrre D A.Is Employment Travel Risk Expenditure Productive?[J].Journal of Monetary Economics,2015,(23).
[5] Gienrue.Is Travel Risk Expenditure Stimulative?[J].Contemporary Pol⁃icy Issues,2015,(7).
[6] Weber P.Theory of the Travel Industry Location of City[M].Chicago:The University of ChicagoPress,2007.
[7] 靳庭良.单整变量之间Granger因果关系的一种检验程序[J].数量经济技术经济研究,2013,(2).
[8] 林毅夫.我国旅游文化发展战略研究[J].南开经济研究,2017,(7).
[9] 李志强.中国结构变动和经济增长中的因果关系和结构断点分析[J].统计与决策,2013,(24).
[10] 曹永福.格兰杰因果性检验评述[J].数量经济技术经济研究,2006,(1).
