非参数部分带测量误差的部分线性模型估计

孙 燕，胡美娣

（上海财经大学a.经济学院；b.数理经济学教育部重点实验室，上海 200434）

0 引言

许多个体和企业的决策需要基于相关经济理论揭示其经济关系与经济活动的数量规律，而经济理论涉及的很多变量往往是无法直接观测到的，如永久收入、效用、能力和预期等。在永久收入假说中，可假定记录的某个个体收入是从某个潜在的、期望为“永久性收入”的收入总体中取出的一个样本，因此用记录的收入来测度永久性收入存在着测量误差。微观调查数据也往往存在着上面提到的“误差”[1]，故随着基于微观调查数据的研究的急剧增加，能处理测量误差的计量方法变得越来越重要。这是因为忽略测量误差很可能会产生内生性问题，导致模型参数估计的非一致性[2]，从而很可能会掩盖变量之间的真实关系，由此得到的推断也是不正确的。如在多数商品消费研究中发现的“increasing dispersion”现象[3]，即随着总消费X的增加，某商品消费Y的波动幅度增大（Var(Y|X)随X的增大而增大），并基于这样的行为特征导出了商品需求规律。但Nadai和Lewbel[4]的最新研究发现“increasing dispersion”现象事实上部分是由测量误差引起的，并不能完全用个人消费行为特征进行解释，这对政策制定有重要的含义。又如陈琳[5]在我国城镇代际收入弹性的估计中纠正了测量误差，由此识别出了纯粹由收入因素导致的变动关系。

另一方面，实际应用中许多经济变量之间很可能存在着非线性的关系，有很多学者研究了解释变量带测量误差的非线性模型的估计[6,7]，但实际问题研究中非线性模型设定的依据往往并不充分，因此很可能存在模型设定偏误问题。于是很多学者开始考虑非参数测量误差模型的估计问题，如Fan和Truong[8]在测量误差分布已知的条件下，利用核卷积方法建立了非参数函数的估计；Schennach[9]及Hu和Sasaki[10]则在能够得到解释变量的另一个不精确观测条件下，验证了非参数函数的可识别性，并基于此建立了非参数估计；Nadai和Lewbe[4]基于工具变量验证了非参数函数的可识别性，并基于广义矩（GMM）方法建立了非参数部分的估计。虽然非参数函数的设定具有很好的灵活性，但当解释变量个数较多时会遭遇“维数诅咒”问题，因此难以在实际应用中得到广泛应用。

半参数模型既能充分利用现有信息，把与被解释变量有明确关系的这部分解释变量或控制变量设为参数形式，又能把与被解释变量关系不够明确的或者是研究感兴趣的这部分解释变量设为非参数形式，这种非参数的设定也为实际应用中参数设定是否合理提供了数据证据和检验的框架。关于半参数测量误差模型的研究，Liang[11]在测量误差分布已知的条件下，给出了非参部分带测量误差的部分线性模型的估计；李小莉[12]则基于带测量误差的解释变量的辅助信息，研究了几种半参数模型的估计问题，但她们仅考虑了线性解释变量部分带测量误差但非参数部分不带测量误差的情形的估计，且其提出的辅助信息在经济学问题中难以获得。

综上，为了得到解释变量存在测量误差时模型未知部分的一致估计，需要新增假定条件，该条件往往被称为识别条件，如测量误差分布已知、存在解释变量的另一个不精确度量或者工具变量等。统计学和计量中关于测量误差模型的研究，较大的差异是模型的识别条件，由此建立了不同的估计。现有统计学中的识别条件概括而言有误差分布已知、误差方差已知或存在大量重复不精确观测，这些条件在经济学问题的研究中往往不成立。不同于现有文献，本文将探讨基于微观经济数据的非参数部分带测量误差的部分线性模型，借鉴Schennach[9]的识别方法，基于核估计、Fourier变换和特征函数建立了模型中未知部分的估计，并将其运用于我国城镇居民食品消费与收入关系的研究中，试图识别出纯粹由于永久收入变动导致的商品消费变动的影响效应。

1 非参数部分带测量误差的部分线性模型

1.1 模型

本文考虑如下非参部分带测量误差的部分线性模型：

其中y为解释变量；z∈R是本文感兴趣的解释变量，但z的观测带有测量误差，即观测到的是w1，u1为不可观测的测量误差；g(·)为未知光滑函数；x∈Rp为其他p个解释变量或控制变量（不含常数项），β∈Rp为未知回归系数；ε为随机误差项。模型（1）既充分利用了先验信息，又具有一定的灵活性，也为实证应用中常见的g(·)的线性设定是否准确提供了一个检验的框架，本文感兴趣的正是g(·)的估计。

虽然本文假定x不存在测量误差，但事实上若x中也存在测量误差，只要x中的测量误差与z独立，则x中的测量误差并不会影响g(·)的估计。同样地，若解释变量y中的测量误差与x，z独立，则y中的测量误差也不会影响g(·)的估计。为简单计，本文假定y中也不存在测量误差。

1.2 未知光滑函数的识别与估计

由于模型（1）中的解释变量z存在测量误差，故仅基于(y，w1，x)的观测样本和现有条件是无法唯一确定未知函数g(·)的。同文献[9]，本文假定可以得到z的另一个不精确测量w2：w2=z+u2，其中u2的期望可以为非零，如微观调查中上一年度的收入数据。若进一步假定E(ε|x，z，u2)=0，E(u1|z，u2)=0，z与u2相互独立，则由文献[9]定理 1及文献[10]定理1可得，基于样本 (y，w1，w2，x)，模型（1）中的未知函数g(z)是唯一确定的（即是可识别的）。

为了得到非参部分g(z)的估计，本文采用二步估计方法，即先假定回归系数β已知，利用非参数测量误差模型的估计方法得到g(·)的初始估计，然后将其代入模型（1）并利用非线性最小二乘法得到β的估计，最后将代入得到g(·)的最终估计。具体地：

步骤1：假定参数β已知，(w，w，xj)为样本数据，则可得g(·)的初始估计为（其估计过程见下文）：

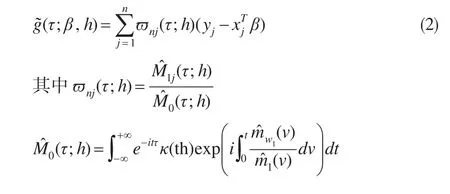
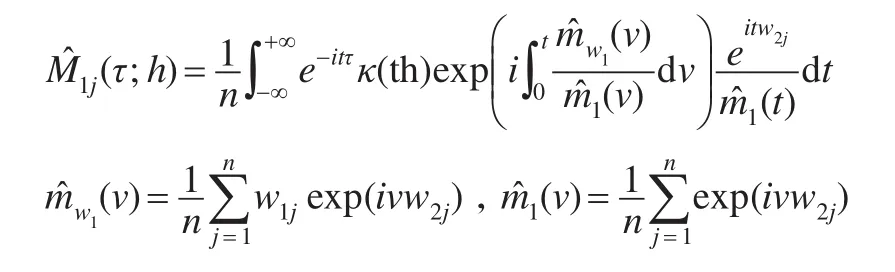
κ(·)表示核函数K(·)的Fourier变换。

步骤2：将估计式（2）代入模型（1），并利用非线性最小二乘法可得β的估计为:

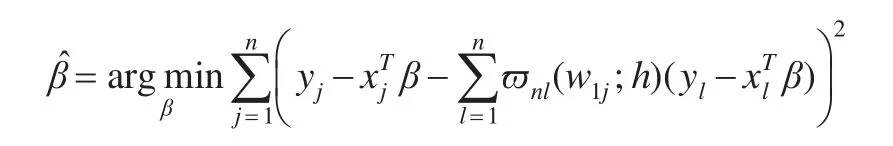
求解该最小化问题可得：

其中：

步骤3：将式（3）代入式（2）即可得g(·)的最终估计。

1.3 回归系数已知时非参数估计式（2）的导出

回归系数β已知时，上文给出的非参数函数估计式（2）并不是显而易见的，本文将给出式（2）的估计过程。若模型（1）中的z可观测，则在回归系数β已知时，模型（1）中非参数函数g(·)在点τ处的常见核估计为式（4）的矩估计：

其中Y=y-xTβ，Kh(·)=K(·/h)/h，K(·)为核函数，h为窗宽。

这里的问题是z是无法观测的，能观测到的是存在测量误差的w1和另一个不精确度量w2。综合借鉴文献[8]、文献[9]定理1的方法，本文将基于式（4）给出式（2）中g(·)的初始估计。具体地：

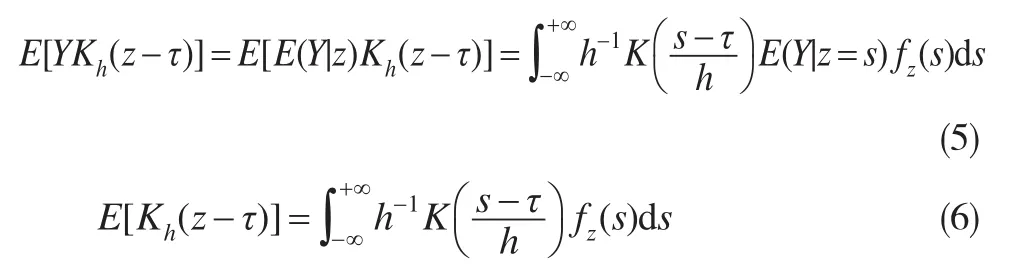
其中fz(·)为z的密度函数。记i=，则K(·)的Fourier变换为

故

将其代入式（5），通过变量代换及积分顺序交换可得：

同理可得式（6）可化为:

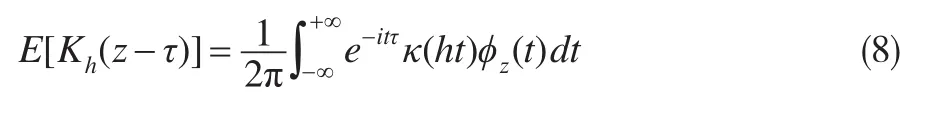
其中ϕz(t)=E(eitz)为随机变量z的特征函数。

下面结合文献[9]定理1和文献[10]定理1的方法给出式（7）、式（8）中 未 知 部 分E(Yeiωz)和ϕz(t)的 基 于(y，w1，w2，x)的表达式。

因为w2=z+u2，z与u2相互独立，故基于特征函数性质可得：

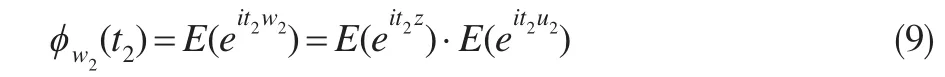
又经计算可得二维随机变量(w1，w2)的特征函数为ϕw1w2(t2)=E(eit1w1+it2w2)，于是由E(u1|z，u2)=0 ，z与u2相互独立可得：

同理由 (Y，w2)的特征函数ϕYw2(t，t2)=E(eitY+it2w2)，式（9）及条件E(ε|z，u2)=0，z与u2相互独立，可导出：

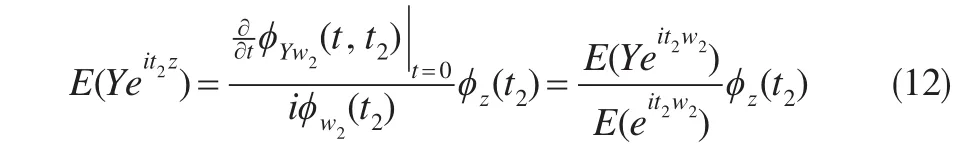
将式（11）、（12）分别代入式（7）、（8），并用样本矩替换总体矩即可得估计式（2）。

2 Monte Carlo模拟

下面将采用Monte Carlo模拟研究验证估计量在实际运行中的表现。数据真实生成过程为：y=xTβ+g(z)+ε,β=0.75，w1=z+u1，w2=z+u2，本文能观测到的就是(y，w1，w2，x)的数据。考虑如下三个不同非参数函数设定的数值模拟例子：

例1：

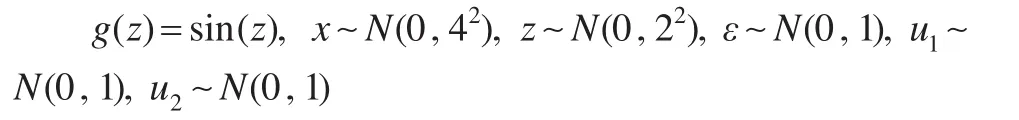
例2：

例3：

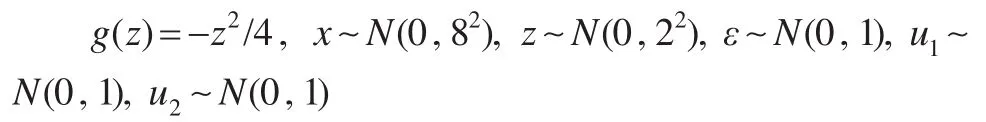
在这三个例子中，考察了不同的非参数函数设定形式，且在第二个例子中，允许第二个观测的测量误差u2均值不为0。另外，在上述三个模拟例子中，带测量误差部分的解释变量其信号噪音比为4:1，观测到的数据中测量误差占比20%，应该不算太大。分别从相应的模型中独立抽取样本容量n=200，500的样本，重复抽取500次，生成样本容量相同的500个仿真数据集。基于文中的估计方法，使用Silverman[13]提出的经验准则选择带宽h，即h=1.06*σ^*n-1/5，其中σ^是w1的样本标准差。

为了比较本文估计的效果，在模拟计算中本文还分别给出了无测量误差的核估计（即将z的数据代入）作为基准，并与带测量误差的核估计（即将z替换为w1）进行对比。这里同样使用两步法给出这两个核估计，即：

步骤1：假定参数β已知，利用NW核估计方法，得到g(·)的初始估计：

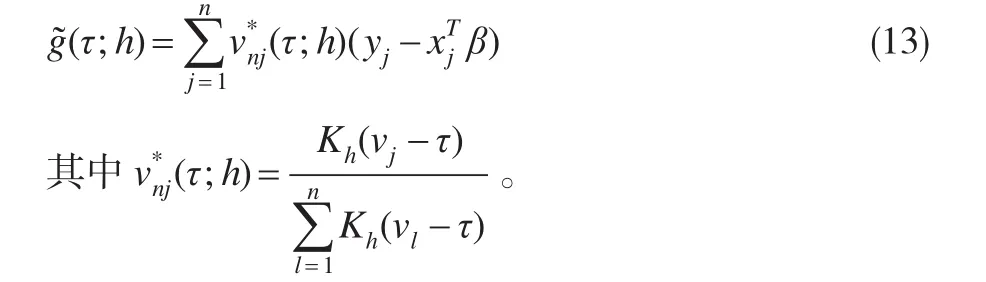
步骤2：将非参数初始估计式（13）代入模型（1），并利用非线性最小二乘法可得β的估计为：

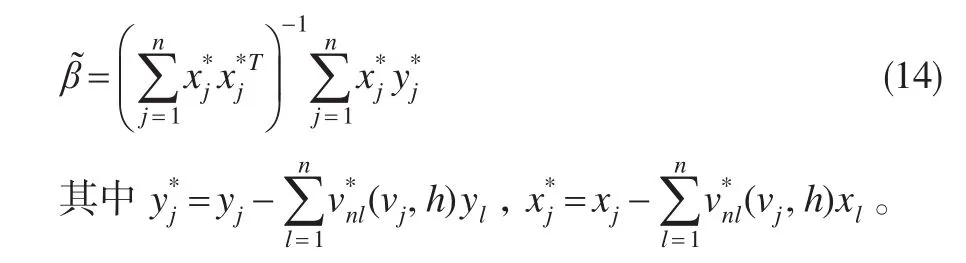
步骤3：将式（3）代入式（2）即可得g(·)的最终估计。

无测量误差下g(·)的核估计为用各zj替换上述步骤中相应的vj（记为NW noerror）；而带测量误差的g(·)核估计为用各w替换上述步骤中相应的vj（记为NW error）。本文NW估计均采用标准正态核，估计结果如图1至图6所示，其中从左至右分别是本文的估计、NW error的估计和NW noerror估计。图中实线表示函数真实值，五条虚线从上至下分别表示非参数估计的90th、70th、50th、30th、10th分位数。由图可见，本文非参估计的中位线几乎与真值重合，且比不考虑测量误差的NW error估计偏差小，尤其在曲线的曲率比较大的地方表现得更为明显。而且在本文的例子中，可观测数据中的测量误差占比较小为20%，可见测量误差的存在导致NW error的核估计偏差较大，尤其在非线性部分偏差更大。显然，随着样本容量的增大，本文提出的非参数部分估计越来越靠近真实曲线。

图1 g(z)=sin(z)时非线性部分估计结果（N=200）

图2 g(z)=sin(z)时非线性部分估计结果（N=500）

图3 g(z)=exp(z)/(1+exp(z))时非线性部分估计结果（N=200）

图4 g(z)=exp(z)/(1+exp(z))时非线性部分估计结果（N=500）

图5 g(z)=-z2/4时非线性部分估计结果（N=200）

图6 g(z)=-z2/4时非线性部分估计结果（N=500）

3 实例应用

根据Friedman[14]的永久收入假说，消费仅依赖于家庭的永久收入。然而，由于永久收入是不可观测的，研究者们往往使用家庭的历史或者当前收入作为其观测值，显然数据中存在着测量误差。本文将基于中国居民收入调查数据库（缩写CHIP）2002年城镇居民的数据，利用模型（1）研究食品消费与收入的关系。本文假定收入消费的函数形式g(·)未知，这种非参数的设定方法能给实证应用中参数形式的设定是否准确提供数据证据。除了收入之外，还有其他因素会影响消费，如袁志刚和宋铮[15]认为人口年龄结构的变化改变了城镇居民的消费行为。因此本文在模型中加入了人口结构的控制变量。由于我国国土辽阔，各地区经济发展水平、消费习惯和客观环境不同，因此，将分东、中、西三组分别探讨城镇居民家庭食品消费与收入的关系。

3.1 数据说明

家庭人口结构变量包含家庭人口年龄结构变化和人口总数变化两个概念，根据邵钢[16]对不同的年龄组食品消费水平的系数假设，本文将家庭成员按年龄分成儿童组：0～14岁、成人组：15～60岁以及老人组：60+岁，并将儿童组和老年组都按0.8折算成标准人，对家庭内所有成员按标准人进行加总得到家庭总标准人量，并取对数作为本文家庭人口结构变量。收入是家庭总年收入（元/年），消费是家庭总年消费（元/年）。本文删掉了其中有缺失数据的样本。数据描述性统计见表1。

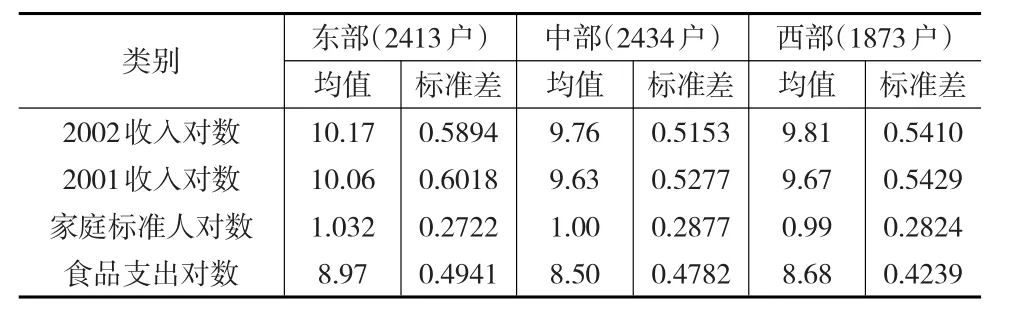
表1 数据的描述性统计

3.2 估计结果

基于模型（1），其中g(·)表示控制人口结构后，东中西三地区的永久收入与食品消费的关系，其斜率表示食品消费的收入弹性；利用上文的估计方法得东中西三地区的永久收入对数与食品支出对数关系g(·)估计如图7所示。由此可见，各个地区食品支出对数与家庭收入对数关系大体呈线性关系，这也验证了在食品消费与收入关系研究中的对数线性模型设定是合理的。且在相同收入水平下，中部地区食品支出最少；而在低收入和高收入水平下，东部地区食品支出最多。程兰芳[17]将东部地区2002年食品支出比重大的原因归于东部地区在肉禽品、奶制品以及外用餐等项上消费支出远远高于中西部地区。而中部地区收入水平较低，因而物价水平更低，从而导致相同收入水平下，中部地区家庭食品支出最小。

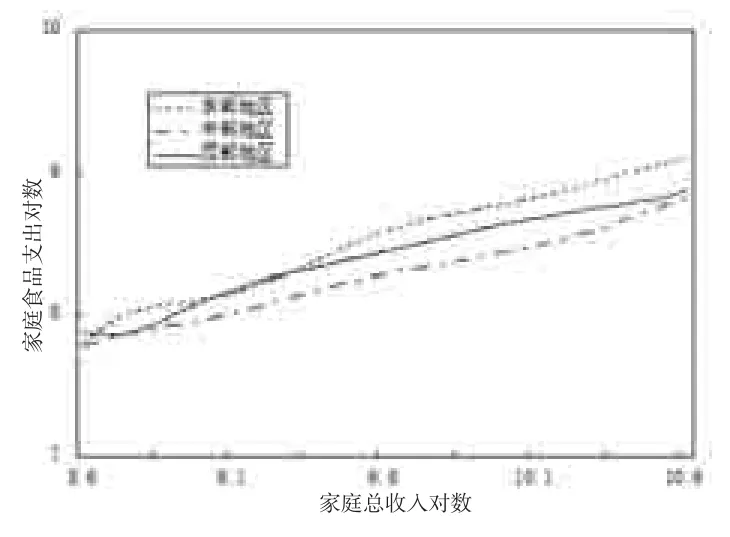
图7 家庭食品支出对数与家庭收入对数关系

4 结论

测量误差的存在往往导致模型存在内生性问题，忽略它将使得线性和非线性模型的估计非一致，因此，本文研究了非参部分带测量误差的部分线性模型的估计，该模型的设定具有很大的灵活性，能防止模型设定偏误导致感兴趣变量估计的非一致性，也为实证应用中参数形式的设定是否合理提供了数据检验的方法。本文在带测量误差的解释变量存在另一不精确度量的前提下，结合核估计、Fourier变换和特征函数方法建立了非参数部分的两步估计。蒙特卡洛模拟结果表明本文的估计量在估计非线性部分时更好，偏差较小。最后本文将该模型及方法运用于我国城镇家庭食品消费与收入关系的估计上，结果发现样本数据支持对数线性模型的设定，更严格的统计检验有待进一步的研究。

参考文献：

[1] Griliches Z.Economic Data Issues,in:Z.Griliches and M.D.Intriliga⁃tor,eds.[M].Amsterdam：North-Holland,1986.

[2] Fuller W.Measurement Error Model[M].New York:Wiley,1987.

[3] Hildenbrand W.Market Demand:Theory and Empirical Evidence[M].New Jersey：Princeton University Press,1994.

[4] Nadai M,Lewbel A.Nonparametric Errors in Variables Models With Measurement Errors on Both Sides of the Equation[J].Journal of Econometrics,2016,(191).

[5] 陈琳.中国城镇代际收入弹性研究：测量误差的纠正和收入影响的识别[J].经济学（季刊），2015,(1).

[6] Carroll R J,Ruppert D,Stefanski L A.Nonlinear Measurement Error Models[M].New York:Chapman and Hall,1995.

[7] Schennach S M.Instrument Variable Estimation of Nonparametric models[J].Econometrica，2007,(75).

[8] Fan J,Truong Y K.Nonparametric Regression With Errors in Vari⁃ables[J].Annals of Statistics,1993,(3).

[9] Schennach S M.Nonparametric Regression in the Presence of Mea⁃surement Error[J].Econometric Theory,2004,(20).

[10] Hu Y Y,Sasaki Y.Closed-form Estimation of Nonparametric Mod⁃els With Non-classical Measurement Errors[J].Journal of Economet⁃rics,2015,(185).

[11] Liang H.Asymptotic Normality of Parametric Part in Partially Linear Models With Measurement Error in the Nonparametric Part[J].Jour⁃nal of Statistical Planning and Inference,2000,(86).

[12] 李小莉.带测量误差的半参数以及结构非参数模型的统计推断[D].上海：上海财经大学博士学位论文，2012.

[13] Silverman B W.Density Estimation for Statistics and Data Analysis[M].London:Chapman and Hall,1986.

[14] Friedman M.A Theory of the Consumption Function[M].Princeton:Princeton University Press,1957.

[15] 袁志刚，宋铮.人口年龄结构、养老金保险制度与最优储蓄率[J].经济研究，2000,(11).

[16] 韶钢.家庭构成对恩格尔曲线的影响[J].数量经济技术经济研究，1985,(10).

[17] 程兰芳.中国城镇居民家庭经济结构研究[D].北京：首都经济贸易大学博士学位论文，2004.