《概率论与数理统计》课程教学创新探索
2018-05-21李宾
李 宾
(吉林大学数学教学中心,吉林 长春 130021)
一、前言
《概率论与数理统计》课程是高等院校理工科专业的一门重要的基础课,也是许多专业研究生入学考试的必考内容,其概念繁多、理论抽象、方法独特,与各专业的其他课程联系紧密。学习这门课不但为后续课程的学习奠定了基础,拓展了视野,也对培养学生的逻辑思维能力、数学建模能力和运用概率统计方法解决实际问题的能力有着极其重要的意义。然而,传统的教学模式和方法往往是“就理论讲理论、就概念讲概念”,枯燥乏味,不能很好地解决学生对抽象的概念和理论理解的难题,使得学生往往因在学习中遇到理解困难而产生抵触情绪,学习兴趣不浓。因此迫切需要对传统的教学模式进行改进,将Mathematica数学软件引入到传统教学中就是一种新的尝试和创新。
Mathematica是1988年由美国Walt Research公司开发的一款综合数学软件包,其操作简单,易学好用。通过编制简单的程序可以解决大量复杂的数学问题,它不但拥有强大的数值计算和符号运算能力,还拥有很强的绘图功能,可以绘制数学上的各种二维和三维图形。将Mathematica软件应用到教学中,用先进的现代化技术辅助数学教学,可以有效地弥补传统教学中的不足,提高教学效果。这样不但能加深学生对抽象概念和理论的理解,还能增强他们的学习兴趣,同时也为学生在以后的学习工作中应用数学知识自行解决实际问题打下基础。
二、利用Mathematica软件显示常用分布的图形
《概率论与数理统计》课程中有很多需要通过图形表示的量,如离散型随机变量的分布律、连续型随机变量的概率密度以及随机变量的分布函数等等。准确地绘制这些函数的图形对于学生深刻理解随机变量的统计规律性有着重要的意义。利用Mathematica软件的绘图功能,可以非常容易地准确地画出函数图形,给学生直观清晰的印象。
图1是二项分布B(20,0.3)的概率分布图。图2是σ=1,μ取不同值时的正态分布概率密度图形;图3是μ=0,σ取不同值时正态分布概率密度图形,通过图形能非常直观地看出μ是‘位置’参数,而σ是‘形状’参数。
对于二维正态分布,其概率密度的表达式较为复杂,很难想象其图形,用Mathematica软件可以很容易地绘制出它的三维立体图,如图4所示。利用该软件的可视化,还可以从不同角度观看立体图形。再比如对于统计中的三大分布,可以把不同自由度对应的概率密度曲线图画在同一坐标系中,这对学生了解三大分布的特征、学习三大分布的上α分位点等都有很大帮助。图5所示的是自由度分别为2、6、9、12、16和22的x2分布的概率密度曲线图,从中很容易看出x2分布概率密度曲线的重心随着自由度的增加逐渐向右下方移动这一特点。

图1 的概率分布图
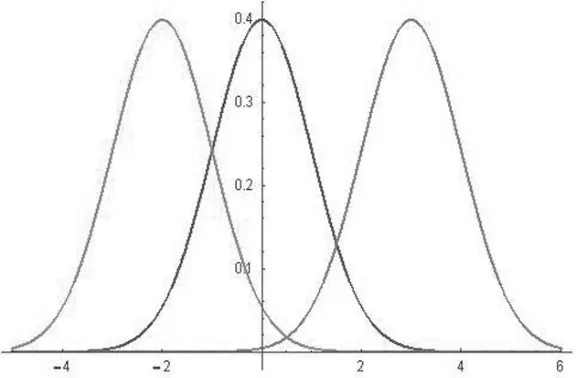
图2 σ=1,μ不同的正态分布图

图3 μ=0,σ不同的正态分布图

图4 二维正态分布概率密度图

图5 不同自由度的分布的概率密度图
三、利用Mathematica软件简化繁琐的推导
在概率统计中,有些定理和结论的推导证明往往需要运用高等数学知识,且需要一定的技巧,课堂推导证明耗时长,一些学生因高等数学知识的欠缺陷入对某一步的思考,无法跟上老师推导的进度,导致教学效果不佳。例如在推导二维正态分布的协方差时,其方法就是用变量替换法计算二重积分,但推导过程繁琐、技巧性强、篇幅也较长。所以在讲授时只简单介绍推导的思路,而推导过程用Mathematica软件编程运算结果代替,只需输入Mathematica软件的命令:

就得到二维正态分布的协方差结果:。
这样做充分利用了Mathematica软件的符号运算能力,用软件运算代替了繁琐的不必要的手算推导,既得到了协方差的结果,又避开了难点,也节省了课上时间,给学生留下了深刻的印象,也激发了他们的好奇心与学习兴趣。
四、利用Mathematica软件演示随机变量的相关性
相关系数是概率统计中的一个重要的数字特征,它表示两个随机变量的线性相关的程度。当两个随机变量的相关系数等于零时,称这两个随机变量不相关。在学习这部分内容时,学生大多并不理解,只能机械地背记相关系数的公式和性质。为了使学生能直观的理解这部分内容,通过下面的例子,再利用Mathematica软件绘制的散点图,非常直观地演示了两个随机变量正线性相关、不线性相关以及负线性相关的各种状态,对学生理解相关教学内容很有帮助。
设随机变量 T 服从[0,2π]上的均匀分布,X=sinT,Y=sin(T+a),(a为常数),讨论随机变量X和Y的相关系数和(线性)相关的情况。
由协方差公式计算可得X和Y的相关系数为ρXY=cos(a),然后利用 Mathematica软件产生服从[0,2π]上均匀分布的 100 个随机数,对 a=0,π/6,π/4,π/3,π/2,π 分别用Mathematica软件绘出X和Y的散点图。当a=0时,ρXY=1,X与Y(线性)正相关,这时X和Y的散点图呈一条直线,X与Y几乎就是线性关系,如图6所示;随着a的逐渐增大,相关系数ρXY的值逐渐变小,X与Y的线性关系逐渐变弱,其散点图也由扁椭圆逐渐变大,如图7、图8和图9所示;当a=π/2时,ρXY=0,X与Y没有线性关系(不相关),这时X和Y的散点图形成一大椭圆,如图10所示;当a从π/2逐渐增大到π,X与Y的线性关系逐渐变强;当a=π时,ρXY=-1,X与Y又几乎是线性关系,这时X和Y的散点图又形成一条直线,如图11所示。
五、利用Mathematica软件验证辛钦大数定律

图6 时的散点图

图7 时的散点图
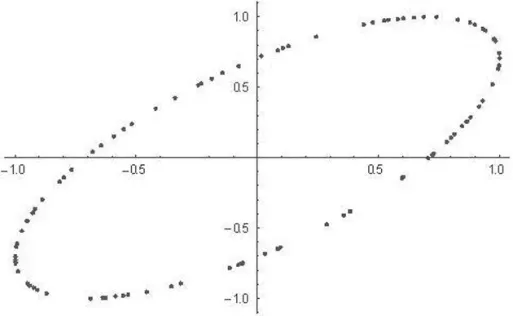
图8 时的散点图
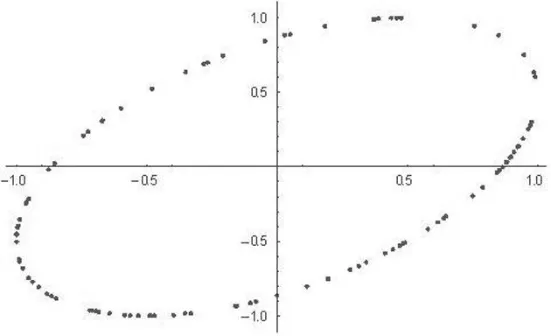
图9 时的散点图
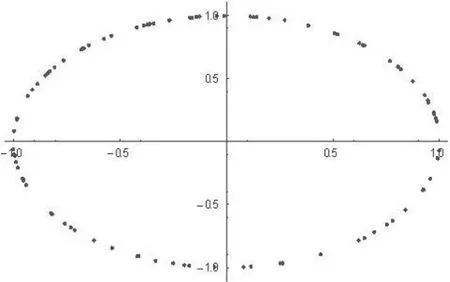
图10 时的散点图
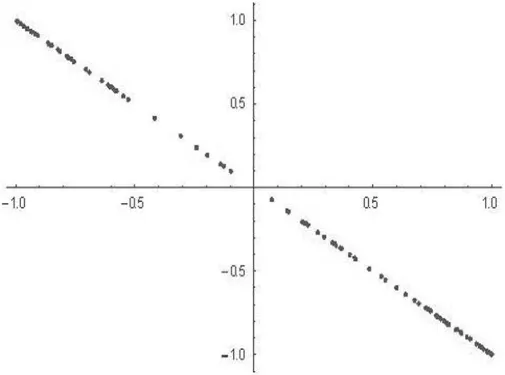
图11 时的散点图
大数定理是概率统计中的非常重要的定理,它揭示了n个相互独立的随机变量的算术平均当n→∞依概率收敛于其数学期望。大数定理非常抽象,很难理解。为了帮助学生更好地理解大数定理的含义,利用Mathematica软件给出了大数定理的直观演示。例如在讲授辛钦大数定理时,就利用Mathematica软件中的Random命令,产生n个相互独立且都服从正态分布 N(2,32)的随机变量 X1,X2,…,Xn,考察当随机变量个数n逐渐增多时,它们的算术平均值的变化情况。下面分别给出了当n=50、1000、3000三种情况下,n个随机变量的算术平均值的分布情况。从图12可以明显看出,当n=50时,50个相互独立的随机变量的算术平均与μ=2有较大的距离。但随着n越来越大了,n个相互独立的随机变量的算术平均越来越密集在μ=2这条直线附近,如图13和图14所示。通过这种方式把抽象定理的结果通过图形直观的演示了出来,使学生耳目一新印象深刻,达到了很好的教学效果。
对《概率论与数理统计》课的教学进行改革和创新,运用Mathematica软件辅助课堂教学,弥补了传统教学的许多不足,不但能方便准确地画出各种二维和三维图形,避免一些繁琐的技巧性较强的推导,还能对抽象的定理和结论给出直观清晰的解释和说明,同时也节约了课堂教学的宝贵时间,活跃了课堂气氛,突破了学生因高等数学知识的欠缺而产生的畏难心理障碍,激发了学生的学习兴趣和自主学习解决问题的积极性,给教学注入了活力,有效地提高了教学效果。相信随着不断将新技术与传统教学方法的有机地结合,必将大大地提高《概率论与数理统计》课程的教学效果。
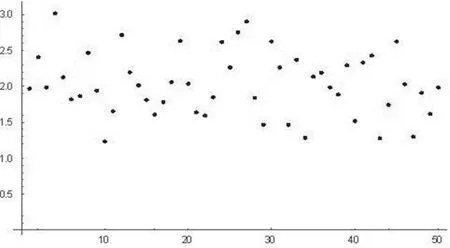
图12 n=50时的散点图

图13 n=1000时的散点图
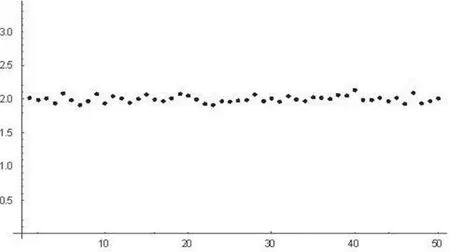
图14 n=3000时的散点图
参考文献:
[1]马淑兰.概率论与数理统计课程教学引入数学实验的尝试和思考[J].内江师范学院学报,2013,28(10).
[2]林志宝,陈玲菊.数学软件Mathematica及其概率统计应用[J],闽江学院学报,2003,24(5).
[3]董小燕.用数学软件直观演示概率论经典定理[J].北京石油化工学院学报,2004,12(1).
[4]刘雄伟,李建平,胡小荣.利用Mathematica软件改善高等数学教学效果的实践[J].中国教育技术装备,2007,(04).
