经历探究过程提升思维能力——“钉子板上的多边形”教学片段及反思

◇任加顺 顾美华

片段一：初探感知

1.引导观察。

大家观察下面的多边形，按要求数一数，在表格里填一填。（每小格1 平方厘米）

（1）数一数或算一算每个多边形的面积各是多少平方厘米。

（2）数一数每个多边形边上的钉子各有多少枚。

（3）想一想多边形的面积和边上的钉子数有怎样的关系。（如图1）

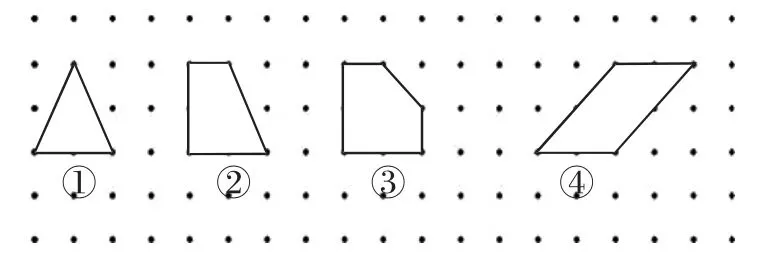
图1

2.交流填表。

通过反馈交流（略），填表1：

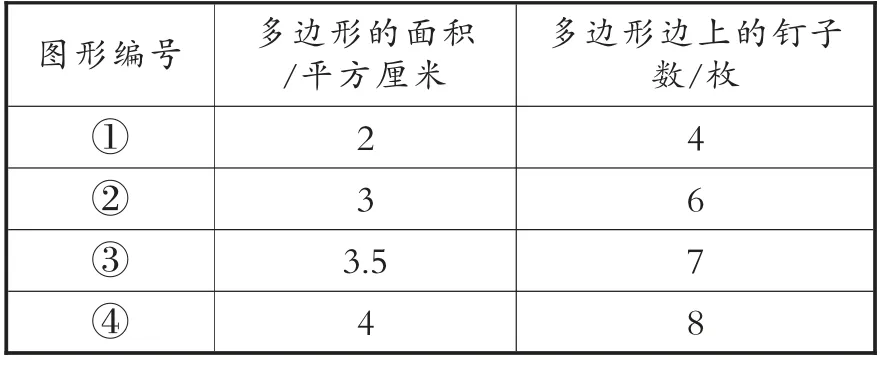
表1

3.观察发现。

师：你能看出这些多边形的面积和边上钉子数的关系吗？

生：多边形边上钉子数是多边形面积的2 倍。

生：多边形的面积是多边形边上钉子数的一半。

生：多边形的面积等于多边形边上的钉子数除以2。

（板书：多边形的面积=多边形边上的钉子数÷2）

师：为了更简洁、方便地表示出这个规律，我们可以用字母来表示。如果用n 表示多边形边上的钉子数，用S 表示多边形的面积，这个规律可以怎样表示？

（生答师板书：S=n÷2）

4．质疑反思。

师：是否钉子板上所有多边形的面积和它边上的钉子数都有这种关系呢？请在下面的多边形中选一个，看看是否也有这样的关系。

（多媒体出示点子图，如图2）

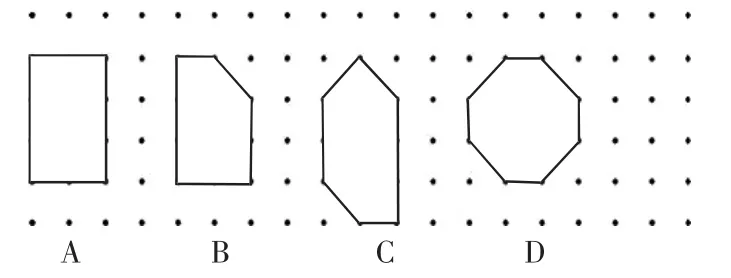
图2

交流（略），填表2：

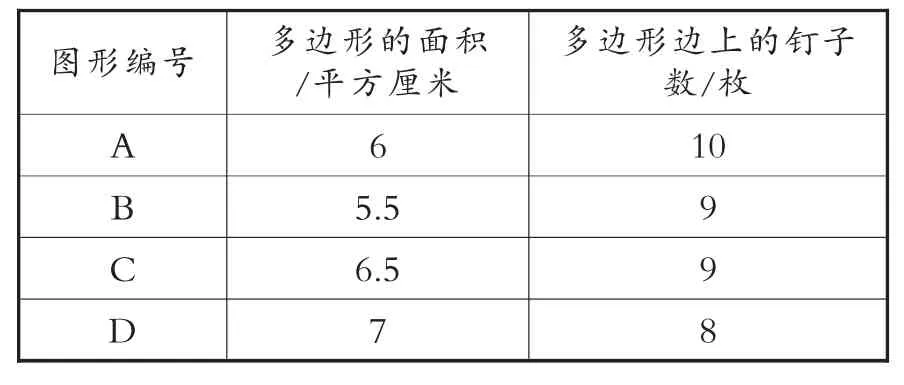
表2

师：现在多边形的面积和边上钉子数还有上面发现的规律吗？这是为什么呢？回过去再看原来的4 个多边形，它们还有什么共同的地方？找找看。现在的4 个多边形与它们有什么不同？

生：原来的4 个多边形内部钉子都只有1 枚。

生：现在的4 个多边形内部钉子不是1 枚，而且不相等，分别是2、3、4 枚。

结合回答，多媒体展示内部钉子闪烁发出声音，并在表1和表2中各增加一栏：多边形内部钉子数/枚。

由此可以看出：多边形的面积不仅与它边上的钉子数有关，还与什么有关？

生：与内部的钉子数有关。

师小结：符合规律的多边形内部的钉子都是1 枚，后面的4 个多边形内部的钉子都不是1枚。这说明多边形的面积不仅与它边上的钉子数有关，还与多边形内部的钉子数有关。刚才我们只是研究了内部钉子数是1 的情况。因此，这个规律，必须加上一个什么条件？

生：多边形内部的钉子数是1。

反思：探究课重在探究，在探究中有所发现，有所收获。 本环节以学生常见的多边形入手，让学生很快发现了第一组4 个图形的规律，既让学生品尝了探究成功的快乐，又为进一步探究埋下了伏笔。正当学生的兴趣被激活，处于愉悦状态时，教师有意质疑：是否钉子板上所有的多边形的面积和它边上的钉子数都有这种关系呢？引发学生进一步探究的欲望，并发现：只有当多边形内的钉子数为1 时，规律才成立。这让学生体会了规律的严密性和探究思考的缜密性。

片段二：再探拓展

1．引发思考。

师：如果多边形内部有2 枚钉子，多边形面积与它边上的钉子数又有什么关系呢？现在请大家进一步观察、比较，看看有没有规律。

2．合作探究。

引导：现在请你们4 人小组合作，按照下面的要求探究多边形的面积。

出示活动要求：

（1）每人画一个内部有2 枚钉子的多边形，数出多边形边上的钉子数，算出它的面积。

（2）每人把获得的数据在小组内交流，并记录在作业纸上的表格中。

（3）观察表格中的数据，小组讨论：你有什么发现？

学生操作、填表、比较、思考，教师巡视。

3．交流发现。

师：组长带着具有代表性的图形上台展示，并现场输入数据，其他组长补充并展示、输入数据。（多媒体出示表格）

……

师：这里多边形的面积还等于n÷2 吗？与n÷2 有什么关系？同桌讨论，看看有什么发现。

生:当多边形内部钉子数是2 时，面积数比多边形边上钉子数的一半多1。

小结：当多边形内部钉子数a=2 时，面积S=n÷2+1。

师板书：a=2，S=n÷2+1。

师追问：检查你画的内部有2 个钉子的多边形，面积符合这个规律吗？如果不符，把你的例子在全班交流。

师：没有反例，说明所有的都符合这个规律。

反思：本环节看似探究多边形内部钉子数是2时，多边形的面积与它边上钉子数的关系，类似于片段一。其实不然，这个环节的探究无论是思维含量还是对学生能力的要求，都有了提升。首先每人自主画图，数钉子数，算出面积；其次小组收集数据、填表；最后通过自主探求、合作交流，在比较、思考中，发现规律，提高了学生的综合探究能力和思维能力。

片段三：猜想验证

1．引发猜想。

师：刚才我们分别探究了多边形内部钉子数分别是1 和2 的情况，那么钉子数a 还可能是几？

生：可能是3、4……

师：根据前面研究的结果，猜一猜，如果多边形内部钉子数是3，它的面积与边上钉子数又有怎样的关系呢。

生：a=3，S=n÷2+2。

追问：如果a=4 或5，又会有什么关系呢？

生：a=4，S=n÷2+3；a=5，S=n÷2+4。

师（引导）：这都是大家的猜想，必须进行验证。这么多的任务，咱们分组验证好吗？

2.分组验证。

出示：小组合作要求：

（1）在组长带领下，每个4 人小组选择一种进行验证。（2）每人画一个“符合要求”的多边形，并算一算面积，数一数边上的钉子数。组长检查后，汇报数据填在表格里。（3）验证面积与边上钉子数的关系式是否正确，小组讨论。

指名学生逐条读。

师：（1）这个要求是什么？（2）“符合要求”的多边形是什么？（可画简单易求面积的多边形）组长检查的是什么？（图形是不是多边形，数据是否正确，图形内部的钉子数是否正确）（3）组长公布组内验证的结果。

小组交流、展示、评价。（过程略）

师追问：有和这个小组一样，验证内部钉子数是3（4、5）个的吗？验证结果与猜想是否一样？有补充吗？

3.推理拓展。

师：同学们真了不起！通过猜测、验证得到了规律。如果a=8 呢？a=100 呢？

生：S=n÷2+7，S=n÷2+99。

师：你们怎么回答得这么快？是怎样想的？

生：多边形面积是它边上钉子数÷2+（多边形内部钉子数-1）。

师板书：S=n÷2+（a-1）。

4.拓展视野。

今天研究的规律，就是数学上著名的皮克定理。有兴趣的同学，可以在网络上或书籍里进一步了解皮克定理。