有界噪声激励下粘弹性碰撞系统的稳定性
2018-05-21谢秀峰李俊林
谢秀峰,李俊林
(太原科技大学应用科学学院,太原030024)
由于粘弹性材料[1]既可以储存能量,又可以耗散能量,因而被广泛用于航空航天、造船、汽车、铁路、建筑、纺织等行业。使得粘弹性系统的动力学行为的研究具有重要的理论意义和工程意义,引起了越来越多学者的关注。关于确定性激励下粘弹性系统的动力学和控制问题已有大量研究。Adhikari[2]研究了粘弹阻尼的线性振子的特征值和定性动力学特征。Potapov[3]研究了非高斯激励下弹性和粘弹性系统的稳定性问题。在实际工程中存在很多随机干扰,其对系统的影响不容忽视,所以研究随机激励下粘弹性系统的动力学行为受到很多学者的关注[4-5]。应用随机平均方法[6],Ariaratnam[7]研究了单自由度线性粘弹性系统的渐近稳定性。Xie[8]研究了有界噪声激励下二维粘弹性系统的矩Lyapunov稳定性。
碰撞是航空航天、机械制造、土木工程等领域广泛存在的一种现象,会影响系统的动态性能,使材料的力学性质发生本质改变,为减少碰撞引起的破坏,碰撞振动系统的动力学行为被广大学者深入研究.由于碰撞问题中含有非光滑因素,增加了动力系统的复杂性[9],光滑系统的很多理论与成果不能直接应用到非光滑系统的分析当中。Dimentberg[10]等利用Dirac delta函数和符号函数对非光滑系统进行光滑化处理,将碰撞系统转化为不含碰撞的动力系统,然后用能量平均法,分析了碰撞振动系统的随机响应问题。应用随机平均法,Xie[11]等研究了高斯白噪声激励下碰撞振动系统的瞬态随机响应。Zhu[12]研究了随机变阻尼的非线性碰撞振动系统的响应问题。Zhao[13]等研究了随机激励下粘弹性碰撞系统的稳态响应。
综上所述,关于粘弹性碰撞问题的相关研究较少,因此有必要研究随机激励下粘弹性碰撞系统动力学行为。本文研究了有界噪声激励下粘弹性碰撞系统的矩稳定性,用恢复系数来描述粘弹性碰撞前后的能量损失,结合Zhuravlev变换和随机平均法给出了系统p阶矩 Lyapunov指数的近似解析解。并讨论了恢复系数、粘弹性系数及随机激励振幅对系统矩稳定性的影响。
1 模型分析
考虑受有界噪声激励的粘弹性碰撞系统可表述为:
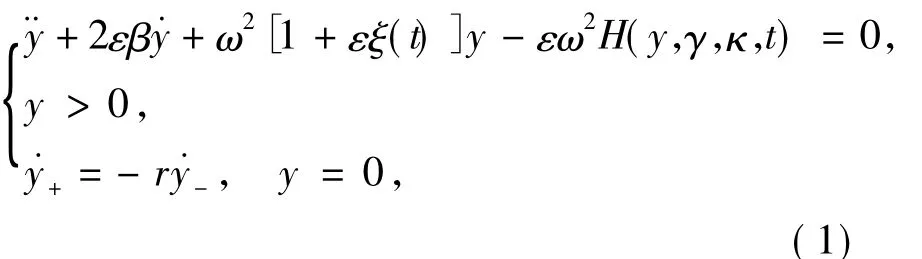
式中:表示y关于时间t的导数;0<r≤1代表碰撞恢复因子;“+”和“-”分别表示碰撞前和碰撞后时刻。β代表系统的阻尼系数,ε≤1为常数。
H表示粘弹性效应,可表示为:
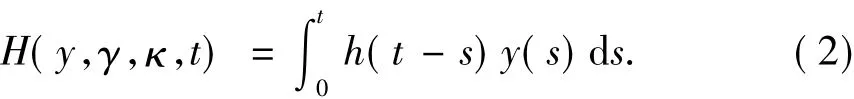
其中,h(t)为粘弹性核函数.
有界噪声ξ(t)可以表示为
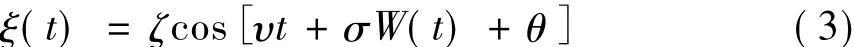
其中,ζ是噪声幅值,σ是噪声强度,W(t)表示标准Wiener过程,θ为[0,2π]上均匀分布的随机变量。ξ(t)的功率谱密度为:

引入非平滑 Zhuravlev变换 y==gn(x),应用Dirac δ函数 δ(x),得到外加项为:(-)δ(t-t*)=(1-r)δ(x).变换后的系统为:
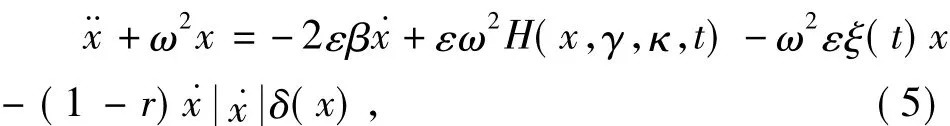
因此,原来的粘弹性碰撞系统(1)转化为新的非连续无碰撞系统(5),其右边的(1-r)δ(x)表示系统的碰撞损失,可以看作外加的阻尼项.ε和1-r都是小参数,记ε^r=1-r.
2 随机平均法
系统(5)的响应可近似表示为:
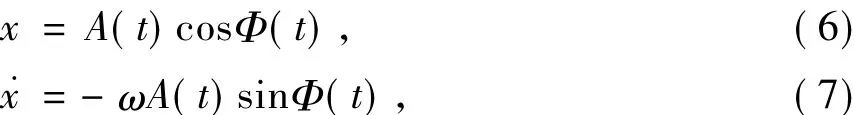
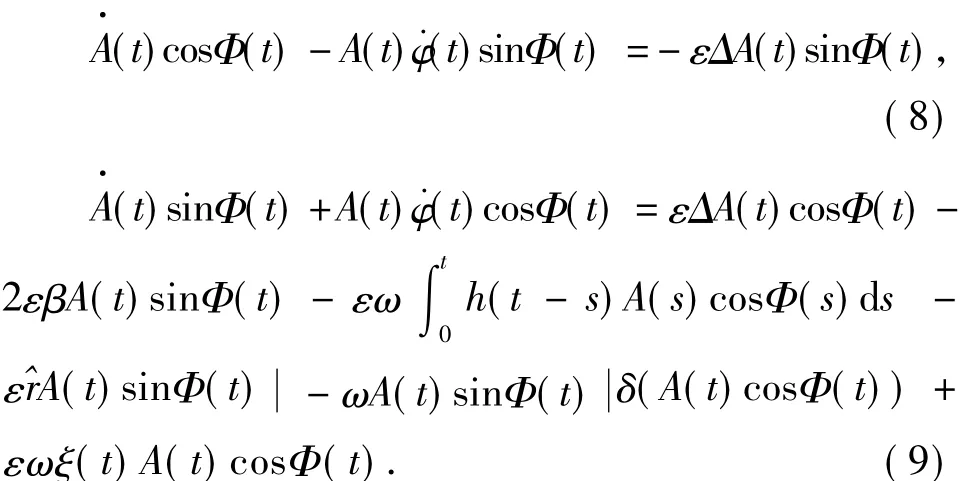
由文献[14]可知,对于一个随机系统的状态变量X(t),其矩稳定性可以用矩Lyapunov指数Λ(p)表示

式中:E[·]表示数学期望,‖·‖2表示二阶范数,系统解p阶矩渐进稳定的充分必要条件是Λ(p)<0,并且Λ'(0)等于系统的最大Lyapunov指数
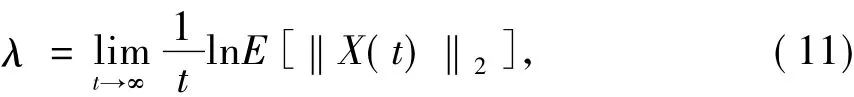
而系统的几乎必然稳定的充分必要条件是λ<0.
为了求出系统的p阶矩Lyapunov指数Λ(p),作变换P(t)=Ap(t),并解式(8)和(9),得P与φ的微分关系:

引入小参数,有界噪声可表示为:
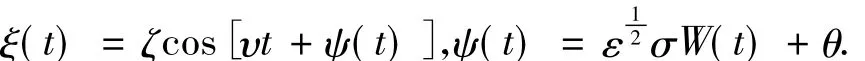
将ξ(t)代入式(13),式(14)中,得:
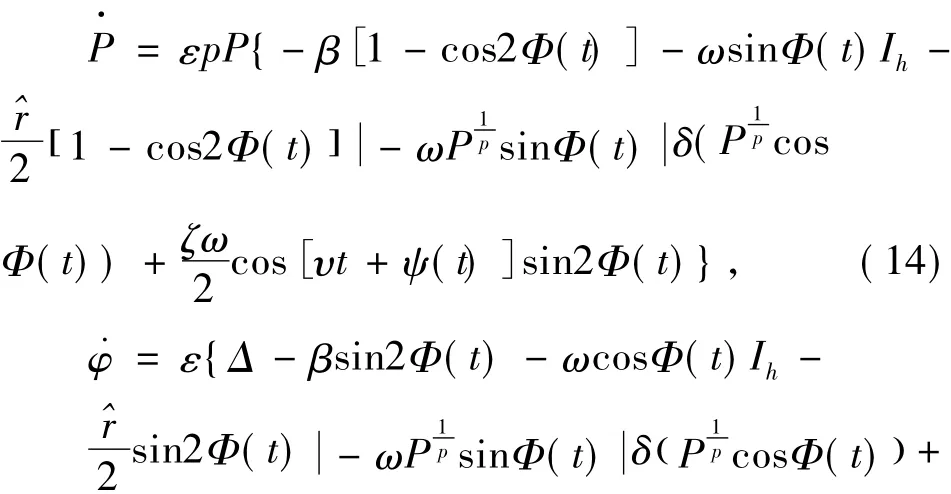
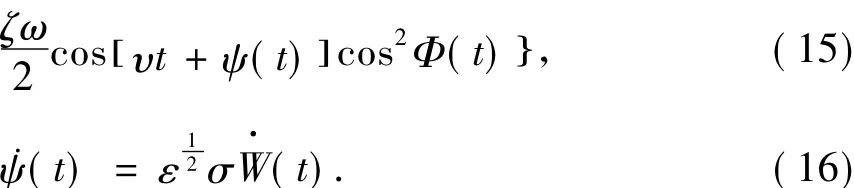
应用随机平均法,得到关于P和φ的平均方程为
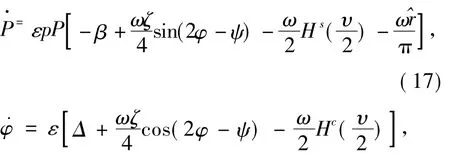
选取Maxwell型粘弹性核函数
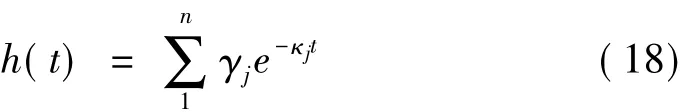
得:

应用变换χ=2φ-ψ,根据Itǒ规则,应用随机平均法,得到关于P和φ的平均Itǒ微分方程为:
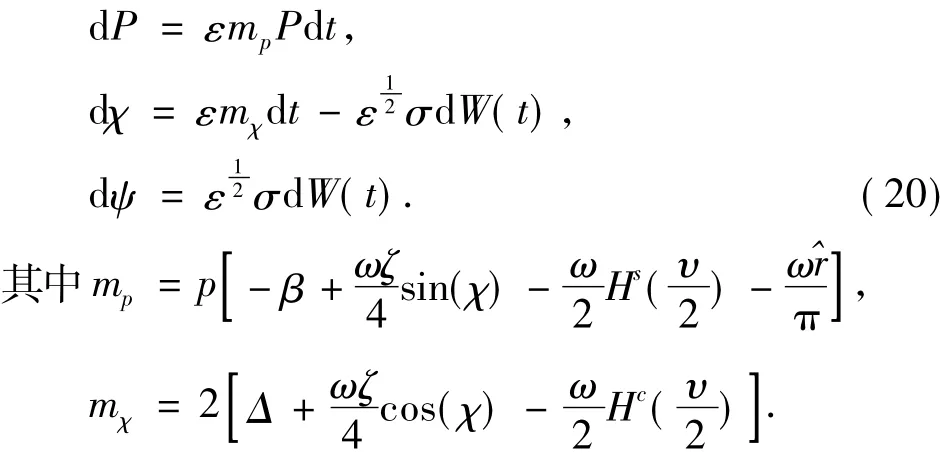
方程组(20)是耦合的,直接求解微分方程组很困难。应用线性随机变换,把p阶矩Lyapunov指数求解问题转化为特征值问题,应用线性随机变换:

其中χ的取值范围是[0,2π].利用Itǒ规则可以将式(21)转化为
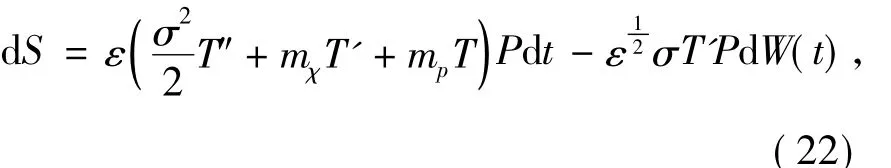
有界非正则变换T(χ)使得P和S有相同的稳定性,使得式(22)的漂移项系数不依赖于χ,有:
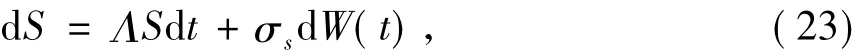
对式(23)两边取数学期望dE[S]=ΛE[S].根据p阶矩Lyapunov指数的定义(10)可知Λ为系统(20)的p阶矩Lyapunov指数。比较式(22)与式(23)的漂移项,得到关于p阶矩Lyapunov指数的特征值问题:
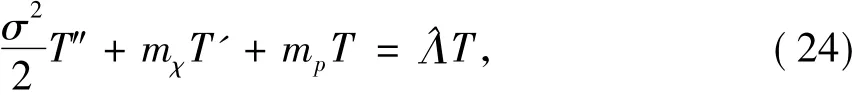
其中Λ(p)=ε^Λ(p).
3 特征值问题的求解
虽然式(1)的碰撞问题转化为特征值问题,但是特征值问题式(24)的精确解析解求解困难。由于式(24)系数的变量χ以2π为周期,因此特征函数T(χ)表示成Fourier级数形式,
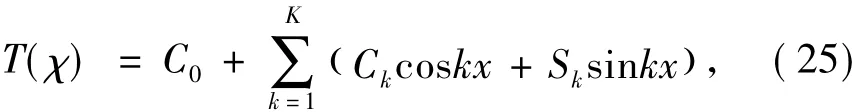
将式(25)代入式(24)得到关于未知参数C0,Ck,Sk的齐次线性代数方程组
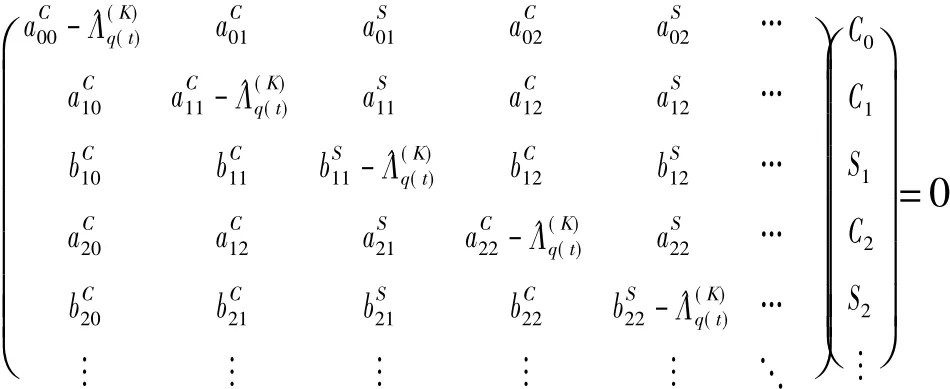
为使C0,Ck,Sk有非零解,系数矩阵的行列式必须为零,得关于近似矩Lyapunov指数(p)的多项式方程
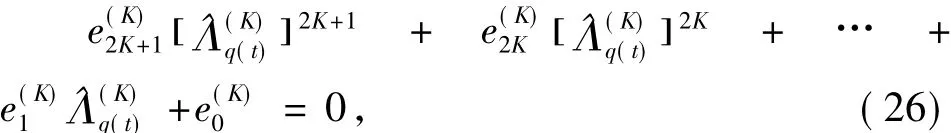
从而系统的矩Lyapunov指数为

当K=0时,T(χ)取为常数 C0,零阶近似矩Lyapunov指数为
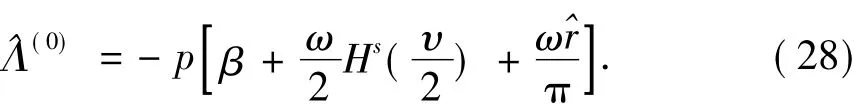
当K=1时,式(26)为三次方程,其系数分别为:
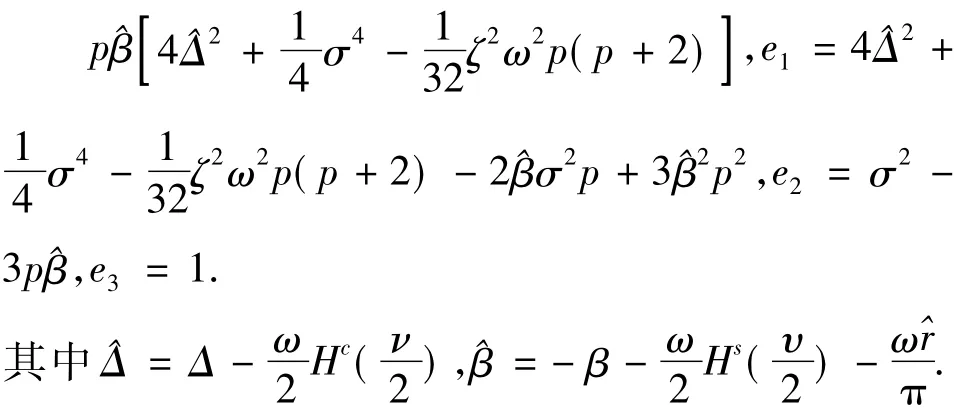
近似矩Lyapunov指数为
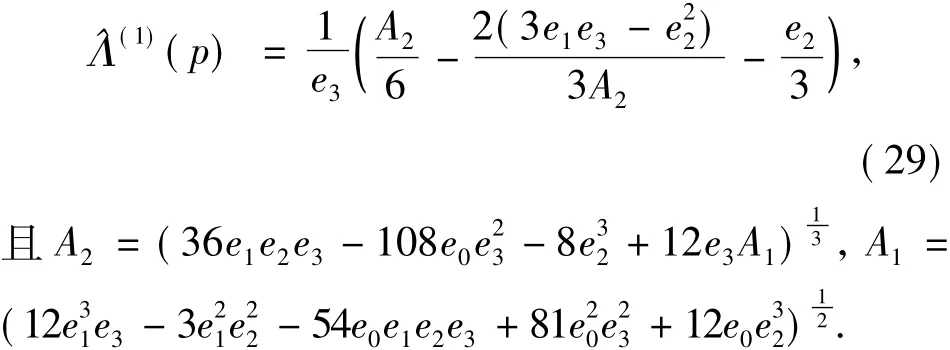
当K>1时,多项式方程(26)没有理论解,可用数值近似解得.
4 稳定性分析
选取粘弹性核函数h(t)=,应 用Maple程序推导出近似矩Lyapunov指数(p)的多项式方程。图1给出当K=1时系统响应的矩Lyapunov指数Λ(p)作为阶数p的函数,随不同的恢复因子r变化的函数曲线,其余系统参数为:ε=0.1,υ =2.0,ω =1.0,β =0.05,σ =2.0,ζ=1.0,γ1= κ1=1,γ2= κ2=0.5,实线表示近似解析解,虚线由Monte Carlo模拟的数值结果。该图表明,在Λ(p)<0的区域内,系统响应的p阶矩渐近稳定,Λ(p)随恢复因子r的增大而增大,即r越大系统的矩稳定性越弱。
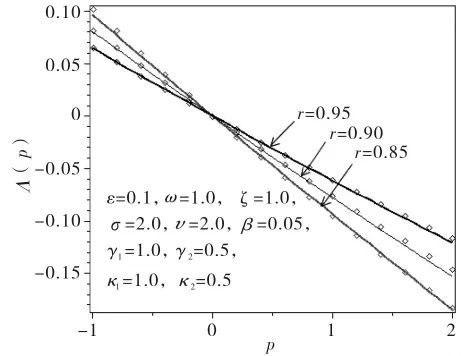
图1 系统的p阶矩Lyapunov指数Fig.1 The pth moment Lyapunov exponent of system(1)
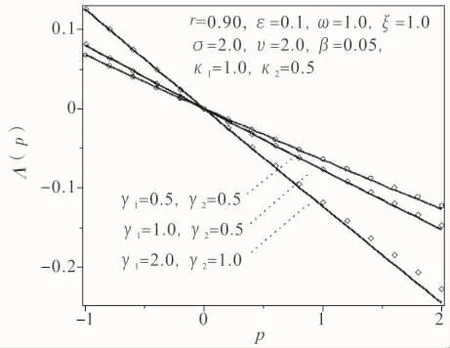
图2 矩Lyapunov指数与不同的粘弹性特征参数γFig.2 The moment Lyapunov exponents for different γ
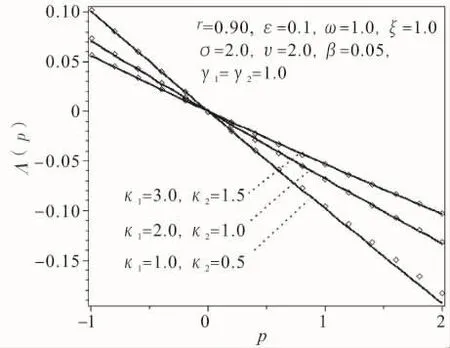
图3 矩Lyapunov指数与不同的粘弹性特征参数κFig.3 The moment Lyapunov exponents for different κ

图4 矩Lyapunov指数与不同的激励振幅ζFig.4 The moment Lyapunov exponents for different amplitude of the parametric excitation ζ
图2 表示粘弹性特征参数γ的变化对矩Lyapunov指数Λ(p)的影响.对于p>0,随粘弹性参数γ增大稳定区域变大,说明粘弹性越强有助于系统的稳定;由图3可以看出矩Lyapunov指数Λ(p)随粘弹性特征参数κ的变化,图3表明松弛时间越长(即κ越小),稳定性越强,说明长的松弛时间有助于系统的稳定。图4给出了矩Lyapunov指数Λ(p)与随机激励振幅ζ的变化关系,取系统参数为:r=0.9,ε =0.1,υ =2.0,ω =1.0,β =0.05,σ =2.0,γ1= κ1=1,γ2=1.0,κ2=0.5,该图表明,随着激励振幅ζ的增大,矩指数变大 ( p >0),可见强的激励振幅使得系统响应的矩稳定性减弱。
5 结论
本文研究了受有界噪声激励下粘弹性碰撞系统的随机稳定性。首先,应用Zhuravlev变换将粘弹性碰撞系统转换为非碰撞系统,然后用随机平均法得到系统的随机微分方程,求得了矩Lyapunov指数的近似解析解,最后通过Monte Carlo模拟数值结果验证了近似解析结果的正确性。讨论了恢复因子、粘弹性参数和随机激励振幅对系统稳定性的影响。研究表明,恢复因子越大系统稳定性越弱;系统的稳定性随粘弹性参数γ的增大,稳定性增强;随松弛时间越长,稳定性越强;强的激励振幅减弱系统响应的稳定性。
参考文献:
[1] GURTIN M E,STERNBERG E.On the linear theory of viscoelasticity[J].Arch Ration Mech Anal,1962,11:291-356.
[2] ADHIKARI S,PASCUAL B.Eigenvalues of linear viscoelastic systems[J].J Sound Vib,2009,325:1000-1011.
[3] POTAPOV V.Stability of elastic and viscoelastic systems under stochastic non-Gaussian excitation[J].Acta Mech,2008,199:167-179.
[4] HAN X,WANG M.General decay of energy for a viscoelastic equation with nonlinear damping[J].J Franklin Inst,2010,347 806-817.
[5] MESSAOUDI S A.On the control of solutions of a viscoelastic equation[J].J Franklin Inst,2007,344:765-776.
[6] 朱位秋.随机振动[M].北京:科学出版社,1992.
[7] ARIARATNAM S T.Stochastic stability of linear viscoelastic systems[J].Probab Eng Mech,1993,8:153-155.
[8] XIE W C.Moment Lyapunov exponents of a two dimensional viscoelastic system under bounded noise excitation[J].ASME J Appl Mech,2002,69:346-357.
[9] 金栋平,胡海岩.碰撞振动与控制[M].北京:科学出版社,2005.
[10] DIMENTBERG M F,IOURTCHENKO D V.Random vibrations with impacts:a review[J].Nonlinear Dyn.2004,36,229-254.
[11] XIE X,LI J,LIU D,GUO R.Transient response of nonlinear vibro-impact system under Gaussian white noise excitation through complex fractional moments[J].Acta Mech,2017,228:1153-1163.
[12] ZHU H.Response of a vibro-impact duffing system with a randomly varying damping term[J].Int J Non-Linear Mech,2014,65:53-62.
[13] ZHAO X R,XU W,GU X D,YANG Y G.Stochastic stationary responses of a viscoelastic system with impacts under additive Gaussian white noise excitation[J].Physica A,2015,431:128-139.
[14] ARNOLD L.A formula connection sample and moment stability of linear stochastic systems[J].SIAM J Appl Math,1984,44:793-802.
[15] DENG J,XIE W C,PANDEY M D.Stochastic stability of SDOF linear viscoelastic system under wide band noise excitation[J].Probab Eng Mech,2015,39:10-22.
