基于极限学习机的小电流接地故障融合选线

梁 喆，杨铁梅

(太原科技大学电子信息工程学院，太原030024)

小电流接地系统发生单相接地故障时，长时间的接地运行极易形成两点或多点接地短路，弧光接地还会引起全系统过电压，破坏系统的安全运行。如何快速准确地排除故障线路，对系统的运行具有重要意义［1-2］。由于单一的故障选线算法中很多对选线有利的故障信息没有得到利用，会导致故障选线时的错选和漏选，其应用具有一定的局限性［3-7］。

前馈神经网络具有良好的学习能力，因此在智能融合选线中广泛应用［8-13］，但此方法大多采用梯度下降法，且网络的隐层节点参数需通过一定的迭代算法进行多次优化，存在训练速度慢、易陷入局部极小点、学习率η的选择敏感等问题。与神经网络算法相比，极限学习机算法(ELM)［14-15］有输入层与隐含层间的连接权值及隐含层神经元的阈值随机产生、学习速度快等优点。因此本文将基于零序导纳法、自适应陷波、改进锁相环的5次谐波方法、小波分析法利用ELM算法进行融合选线研究［16］。

1 极限学习机原理

给定任意Q个不同样本(xi，ti)，其中xi=［xi1，xi2，...，xin］T∈ Rn，ti= ［ti1，ti2，...，tim］T∈ Rm，一个任意区间无限可微的激活函数g:R→R，则对于基于Q个隐层神经元的SLFN，在任意赋值wi∈Rn和bi∈R的情况下，其隐层输出矩阵H可逆且‖H β－T'‖ =0.而给定任意小误差ε(ε ＞0)，总存在一个含有K(K≤Q)个隐层神经元的SLFN，在任意赋值 wi∈ Rn和 bi∈R 的情况下，有 ‖HN×MβM×m－T'‖ ＜ε.因此任意情况下误差都可很小。

因此当激活函数g(x)无限可微时，SLFN的参数不需全部调整，ω和b在训练前可随机选择，β可以通过求解方程min‖Hβ －T'‖ 得β^=H+T'，其中

βH+是隐层输出矩阵H的Moore-Penrose广义逆。

学习算法步骤如下:

(1)确定隐层神经元个数，随机设定ω和b;

(2)选择激活函数(无限可微)，求解隐层输出矩阵 H，其中，Hβ =T'，T= ［t1，t2，...，tQ］m×Q，tj=

(3) 计算输出层权值:=H+T'.

2 基于ELM的故障融合选线

2.1 故障融合选线原理

图2 中性点不接地系统零序导纳波形Fig.2 Simulation of method based on zero sequence conductances in neutral unearthed system

首先在MATLAB中分别建立110/35 kV的基于零序导纳法、自适应陷波、改进锁相环的5次谐波法及小波分析法，应用在小电流系统模型中。其次，分别用小波包变换算法(WPT)提取各模型在不同接地系统、不同接地电阻、不同故障初始角等情况下发生故障时的暂态零序电流信号作为特征分量，然后将采集的数据分为训练集和测试集，将训练集样本输入ELM进行信息融合，获得选线模型，最后将测试样本输入到该模型进行测试。原理图如图1所示。

图1 故障选线原理图Fig.1 Fault line selection principle diagram

2.2 四种模型简述

2.2.1 零序导纳法

零序导纳法(Y故0=I0/Un)在中性点不接地系统中发生故障时的波形如图2所示。

零序导纳法(Y故0=I0/Un)在中性点经消弧线圈接地系统中发生故障时的波形如图3所示。

图3 中性点经消弧线圈接地系统零序导纳波形Fig.3 Simulation of method based on zero sequence conductance in arc suppression coil grounding system

显然故障线路和非故障线路的零序导纳相位相反，非故障馈线的零序导纳的幅值之和与故障馈线的零序导纳幅值相等。

2.2.2 改进锁相环的5次谐波分析

由于故障时谐波电流很小，利用滤波器提取的信号中，其他频次的谐波成分会干扰选线的准确性。因此本文采用改进型的锁相环，其原理图如图4所示。

将得到的曲线利用Simulink中的FFT分析可以得到频谱图，可以看到，通过使用改进锁相环，较准确的得到了5次谐波信号。故障线路的零序电流5次谐波分量约为非故障线路零序电流5次谐波分量的和，而相位也与非故障线路的相位相反。

2.2.3 自适应陷波法

自适应陷波滤波器可通过调节自身的参数自动跟踪到基波信号的变化，有实时、准确的提取信号的优点。原理如图6所示。

图4 改进型锁相环原理图Fig.4 Improved phase locked loop principle diagram

图5 中性点不接地系统5次谐波法波形Fig.5 Simulation of Method Based on Fifth Harmonics of Zero Sequence Current in Neutral Unearthed System

图6 中性点经消弧线圈接地系统5次谐波法波形Fig.6 Simulation of method based on fifth harmonics of zero sequence current in arc suppression coil grounding system

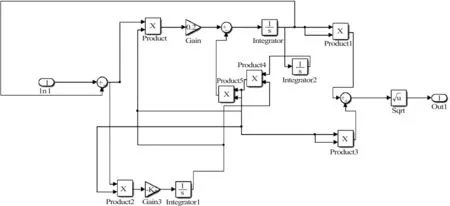
图7 自适应陷波滤波器结构图Fig.7 Structure diagram of adaptive notch filter

图8 中性点不接地系统自适应陷波波形Fig.8 Adaptive notch waveform in neutral unearthed system

图9 中性点经消弧线圈接地系统自适应陷波波形Fig.9 Adaptive notch waveform in arc suppression coil grounding system

2.2.4 小波分析法

小波分析法的选线流程为:

2.3 故障特征量的提取

基于小波包算法的故障特征量具体提取方法如下:

(1)用db6小波包对发生故障时各线路的零序电流信号进行5层分解。

(2)由下式求得每条线路的能量 εij，总能量Eij.

其中(n)为分解后第(j，k)子频段下的系数。选取最大频带为特征频带(除工频外)。

(3)根据式(2)求取各线路的暂态特征值Xm，n.

其中，m为线路数，n为特征频带数。由 上述步骤，得 X= ［X1，1，X1，2，X2，1，...，Xm，n］，从中选取特征典型且包括各种故障类型的特征分量共150组，其中75组用于训练样本，剩下75用于测试样本。

(4)通过极限学习机算法对训练样本进行训练，得到故障选线的模型。

(5)最后用测试样本测试所得模型。

3 实验研究

分别在MATLAB/Simulink中搭建110 kV/35 kV的基于零序导纳法、自适应陷波、改进锁相环的5次谐波方法、小波分析的小电流系统作为故障选线实验仿真模型。共5条线路，线路1发生A相的接地故障，分别采集中性点不接地时及中性点经消弧线圈接地，接地电阻不同(0.001 Ω、1 Ω、5 Ω、10 Ω、1000 Ω)，不同相角(0°、45°、90°)，故障点距母线的距离为 8 km，在0.14 s发生故障时的零序电流。采用的补偿度为10%.表1为模型基本参数。

图10 基于小波变换的故障选线方法流程图Fig.10 Flow chart of fault line selection method based on wavelet Transform

图11 小电流接地系统小波分析波形Fig.11 Waveform of method based on wavelets in arc suppression coil grounding system

表1 模型基本参数Tab.1 Basic Parameters of Model

由实验所得数据较多(按照2.3节的步骤得到)，本文选取其中的150组(5种方法在不同情况下的数据各30组)，将其中的75组作为测试样本，另外75组作为训练样本。

图12、表2所示为各种模型下的极限学习机测试后的结果。以各种模型经2.3节步骤计算后所得的能量特征值为输入，输出“1”为故障，“2”为非故障。表2为部分样本数据及输出结果，表3为ELM与PNN的性能比较。

表2 部分样本数据及输出结果Tab.2 Part of the sample data and output results

图12 测试集预测结果对比(ELM vs PNN)Fig.13 Comparison of prediction results of test set(ELM vs PNN)

4 结论

由实验结果可知，采用ELM算法将零序导纳法、改进锁相环5次谐波法、自适应陷波法、小波分析法的暂态电流信号经过特征提取后的数据进行融合选线，实现100% 精确选线，且选线速度快，不受接地电阻、故障初始角等影响，与单一方法选线相比，由4种模型所得的故障特征向量数据更充分、准确，其中改进锁相环五次谐波法和自适应陷波法更能捕捉到微弱的零序电流信号，防止漏选，本方法适用范围更广。

表3 ELM与PNN的性能比较Tab.3 Performance comparison of ELM and PNN

参考文献:

［1］ 程路，陈乔夫.小电流接地系统单相接地选线技术综述［J］.电网技术，2009，33(18):219-224.

［2］ 姜健，鲍光海.小电流接地系统单相接地故障选线方法综述［J］.电气技术，2015，16(12):1-5.

［3］ ZHANG SHUQING，MA YUE，LI PAN，et al.Application of Improved Generalized Harmonic Wavelet Packet Decomposition and Chaos Oscillator to Fault Line Detection in Small Current Grounding System［J］.Transactions of China Electrotechnical Society，2015，30(3):13-20.

［4］ 殷培峰，刘石红.基于谐波与首半波结合的单相接地选线分析与研究［J］.自动化与仪器仪表，2013，168(4):19-21.

［5］ SUN QIDONG，ZHANG KAIRU，LIU JIAN.Research on single-phase fault earth fault line selection method for the distribution network based on fifth harmonics and wavelet reconstruction［J］.Electrical Measurement ＆ Instrumentation，2016，53(16):1-4.

［6］ 付光杰，盖峰，陈聪，等.基于零序导纳模值差绝对极大值法的定位方法研究［J］.电气自动化，2015，37(6):63-65.

［7］ X Wang，Y Lu，Y Hou.Fault Line Selection Method of Small Current Grounding System Based on Wavelet Packet and Multi Frequency Band Analysis［J］.Digital Content Technology and its Applications，2013，7(6):1176.

［8］ 庞清乐，孙同景，穆健，等.基于神经网络的中性点经消弧线圈接地系统故障选线方法［J］.电网技术，2005，29(24):77-80.

［9］ 李荣明，王官洁，罗建.基于神经网络的小电流接地系统综合智能选线［J］.重庆大学学报:自然科学版，2004，27(5):85-89.

［10］ 曹运刚，陈平，杨茂亭，等.基于人工神经网络的小电流接地故障选线方法研究［J］.国网技术学院学报，2015，18(1):21-25.

［11］ 王晓卫，魏向向，侯雅晓，等.基于小波去噪与改进RBF神经网络的小电流接地系统故障选线方法［J］.工矿自动化，2014，40(4):46-50.

［12］ VAIROOS A，NAVOLOCHNYI AA，OA ONISOVA，et al.Zero-sequence admittance used to protect distribution networks with low earth fault currents［J］.Russian Electrical Engineering，2011，82(1):32-37.

［13］ YF XIONG，S WANG，W ZHANG.A Line-Selection Method of Data Fusion Based on Neural Network［J］.Procedia Engineering，2012，29:520-525.

［14］ 杨乐.张瑞在线序列ELM算法及其发展［J］.西北大学学报:自然科学版，2012，42(6):885-889.

［15］ HUANG G B，ZHU Q Y，SIEW C K.Extreme learning machine:a new learning scheme of feed forward neural networks［C］//Proceedings of the International Joint Conference on Neural Net works(IJCNN 2004).Budapest，Hungary，2004:985-990.

［16］ 吴庆典，王安红.一种基于小波四叉树的无线视频组播方案［J］.太原科技大学学报，2014，35(4):252-257.