级数一致收敛的狄利克雷判别法的相关结论研究

丁 慧 崔国范 王凤玲

（绥化学院信息工程学院 黑龙江绥化 152061；2.黑河学院 黑龙江黑河 164300）

数学分析是数学专业的基础课程，其中判断函数项级数的一致敛散性是一重点及难点问题，其中判别级数收敛的方法很多，如何能深入系统地把握各种方法间的关系，运用判别法灵活、快捷地解决问题是我们积极探索的问题。

一、判别函数项级数一致收敛的方法

判别函数项级数一致收敛的方法有柯西一致收敛原理，M判别法，阿贝尔及狄利克雷判别法等，他们的具体内容如下：

引理1[1]（Cauchy一致收敛原理）级数在D一致收敛的充要条件为：∀ε＞0，∃N，当 n＞N，∀p∈N，∀x∈D，有

引理2[2]（M判别法）设级数un(x)定义在区间D上，是收敛的正项级数。若当n充分大时,对∀x∈D，有则在D上一致收敛。

对于此定理要注意，若级数在区间D上不存在优级数，则不能推出级数在区间D上非一致收敛.

引理3[1]（Abel判别法）设级数满足：

（2）对每个x∈D，数列{vn(x)}单调，且函数列{vn(x)}在D上一致有界,即∃M＞0,使对于∀x∈D，∀n，有 |vn(x)|≤M，则级数在区间D上一致收敛。

引理4[2]（Dirichlet判别法）设级数满足：

（1）级数的部分和函数列在区间D上一致有界；

（2）对于每一个D，数列{vn(x)}单调且在区间D上函数列{vn(x)}一致收敛于零，则级数在区间D上一致收敛。

二、研究结果

凡凡种种的数学分析教材都能指出狄利克雷判别法包含了阿贝尔判别法，狄利克雷判别法还包含了交错级数的莱布尼兹判别法，我们将给出狄利克雷判别法也包含了一致柯西收敛原理,狄利克雷判别法的推广到复数域的形式以及与其他判别法的系统关系图。

（一）狄利克雷判别法包含一致柯西收敛原理。

定理1 若级数满足狄利克雷判别法，则级数满足一致柯西收敛原理。

证明：因为部分和函数列有界，则max{|vk(x)|,|vm(x)}|是有界的，即

同时，由于级数一致收敛，根据柯西收敛原理，对于任意的ε＞0，对于足够大n和k＞n，以及任何x∈E,有

又因为不等式

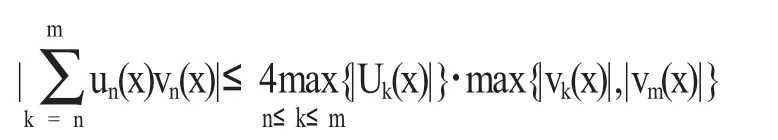
于是，级数满足一致柯西收敛原理。

（二）狄利克雷判别法推广形式。函数项级数一致收敛的狄利克雷判别法不仅在实数域上成立，而且可以推广到复数域上，推广形式如下：

定理 2[3]设 E⊂X，un:X→C,其中 C是复函数，vn:X→R,其中R是实函数，级数满足：

（1）级数的部分和在E上一致有界；

则级数在E⊂X上一致收敛。

由这个定理我们给出为数项级数时，并将条件{vn}弱化为{vn}，其修正后是单调的，且构成绝对收敛级数。

定理3 设E⊂X，un:X→C,其中C是复数，vn:X→R,其中R是实数，级数满足：

（1）级数的部分和在E上有界；

（2）{γn}在 E单调，且构成绝对收敛级数；则级数在E上收敛。

证明:级数的部分和在E上有界，即存在M＞0,使得（不依赖于的常数），则在E上，∀p＞0，恒有

{γn}在 E 构成绝对收敛级数，则满足∀ε＞0，∃N，当 n＞N，∀p∈N，有ε，进而有

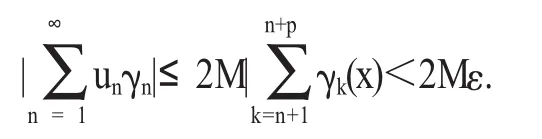
所以级数在E上收敛。

（三）狄利克雷判别法与其他一致收敛判别法的关系图。

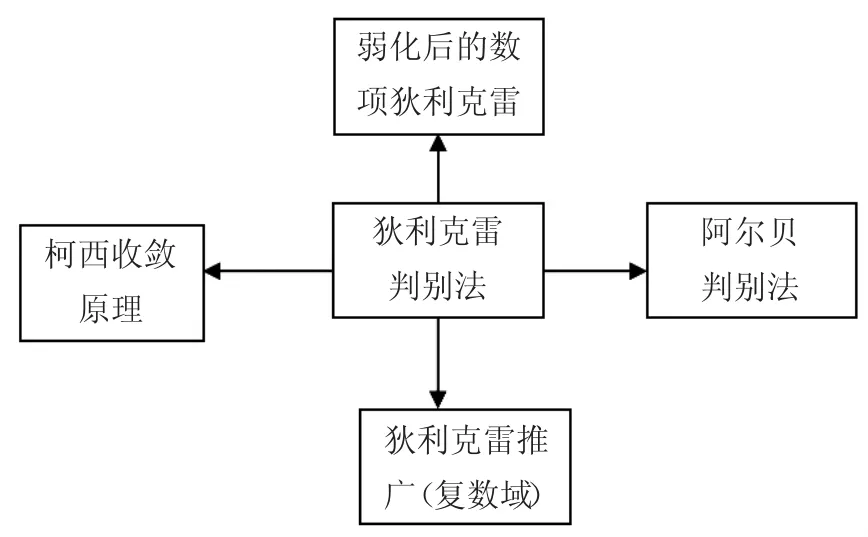
函数项级数一致收敛的狄利克雷判别法包含阿贝尔判别法、柯西收敛原理，同时它也可以推广到对于任意点集的复数域上函数项级数，其中点集可以是有限区间，也可以是无限区间.狄利克雷判别法不仅可以特殊化为交错级数的莱布尼茨判别法，而且可以将数项级数条件弱化为{vn}，当修正后是单调的，且构成绝对收敛级数.

三、结束语

从对于函数项级数一致收敛的狄利克雷判别法入手，详细地论证出了狄利克雷判别法与其它判别法间的关系，展现了知识间的系统联系性.同时，给出狄利克雷判别法的推广及弱化的数项级数的敛散条件，使解决的对象外延扩大，而且便捷有效地解决函数项的一致收敛这一难点问题.

参考文献：

[1]欧阳光中，朱学炎，金福临,等.数学分析（下）[M].高等教育出版社2015：75-88.

[2]刘玉莲.数学分析（下）[M].北京：高等教育出版社，2010：70-75.

[3]B.A卓里奇.数学分析[M].北京：高等教育出版社，2008：330-333.

[4]谢惠民，沐定夷.吉米多维奇数学分析习题集学习指引[M].北京：高等教育出版社，2013：144-145.

[5]文德祥，刘绍武，冯立新.北京大学出版社[M].北京：北京大学出版社，2014：72-75.