基于融合状态递推的非线性联邦滤波器故障检测算法*

卢 航 郝顺义 沈 飞 李保军

空军工程大学航空航天工程学院，西安710038

利用卡尔曼滤波技术对多传感器进行信息融合时有2种途径，集中式卡尔曼滤波和分散化卡尔曼滤波[1]。集中式卡尔曼滤波是利用1个滤波器集中处理所有传感器信息，它可以在理论上得到系统状态的最优估计，但由于其状态维数高，计算负担重，实时性差，且当任意子系统发生故障时，其状态估计都会受到污染，容错性能差，不利于故障诊断。分散化滤波技术的提出很好地解决了上述问题，而在众多的分散化滤波技术当中，Carlson提出的联邦滤波由于其计算量小、设计灵活及容错性能好受到广泛关注，已被美国空军的容错导航系统计划选为基本算法[2-3]。

容错系统设计是为了从系统整体上增强其可靠性，通过监控系统状态，实时检测并隔离故障，将正常系统重新组合，使系统具有自我监控功能，排除由内部故障带来的工作异常，从某种程度上达到提高系统精度的目的[4-6]。容错系统需要实时确定各子系统量测信息的有效性，故在各个子系统中应配备实时的故障检测及隔离算法[7]。早在70年代初，学者们就开始研究动态系统故障检测与隔离算法，发展至今，算法体系已经相对成熟。

本文对联邦滤波器的故障检测算法在非线性滤波框架下进行推广，推导了针对非线性模型的状态χ2检测法，并对算法结构进行改进，提出一种新型故障检测算法。该新型算法结合联邦滤波器的全局最优状态融合和状态递推器获得融合状态递推算法，再由各子系统通过非线性滤波器得到的状态估计与融合状态递推器之间的残差构造检验量，进行故障检测。因为全局最优融合状态的精度高于局部滤波值，所以相对于传统算法，该算法具有更高的检测灵敏度，最后通过一组仿真实验，验证了所提算法的有效性。

1 基于非线性联邦滤波器的故障检测

1.1 非线性系统模型与算法

考虑如下离散非线性系统模型：

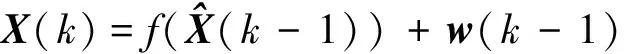
(1)

式中，f(·)为非线性系统方程；h(·)为非线性量测函数；系统状态向量为X(k)∈Rn；量测向量为Z(k)∈Rm；w(k-1)和v(k)为互不相关的高斯白噪声，其方差分别为Q(k-1)和R(k)。

对各子系统采用如下非线性滤波算法：

1.1.1 时间更新

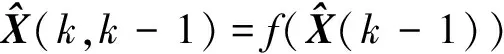
(2)

计算一步预测均方误差P(k,k-1)

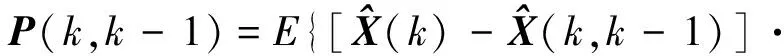
(3)

1.1.2 量测更新

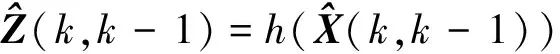
(4)

计算量测一步预测均方误差阵PZ(k,k-1)

(5)

计算状态一步预测与量测一步预测之间的协方差阵PXZ(k,k-1)

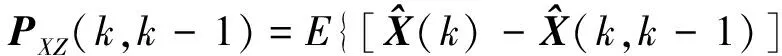
(6)

计算滤波增益K(k)

K(k)=PXZ(k,k-1)(PZ(k,k-1))-1

(7)

计算状态估计均方误差P(k)

P(k)=P(k,k-1)-K(k)PZ(k,k-1)KT(k)

(8)

计算量测一步预测误差r(k)

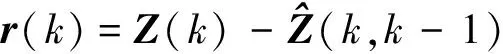
(9)

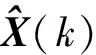
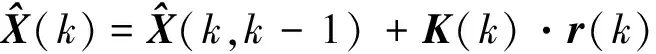
(10)

1.2 联邦滤波器结构

联邦滤波器结构如图1所示：

图1 联邦滤波器结构

联邦滤波采用方差上界技术、信息分配的方法使得各子滤波器估计状态可以按不相关的方式处理[7]，具体算法流程如下：

2) 将主、子滤波器的过程噪声协方差阵按式(23)设置为组合系统过程噪声协方差阵的γi(i=1,2,…,m)倍；

3) 各子滤波器处理自己的量测信息，获得相应估计量；

4) 在得到各子滤波器的局部估计和主滤波器的估计后按式(13)进行最优融合，得到主滤波器的滤波值和方差信息；

5) 用全局融合滤波解重置各主、子滤波器的滤波值和协方差阵。

(11)

(12)

(13)

2 基于融合状态递推的故障检测

2.1 多步融合状态递推器

设联邦滤波器具有N个子系统，每个子系统的量测方程为：

Zi(k)=hi(X(k))+Vi(k),i=1,…,N

(14)

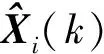
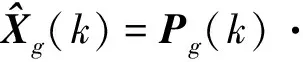
(15)

(16)

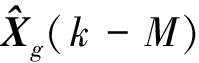
(17)

Ps(k)由下式递推计算：

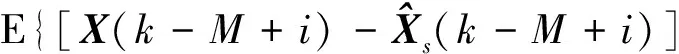
(18)

其中，Ps(k-M)=Pg(k-M)，i=1,…,M。

需要说明的是，重置周期T=M应根据系统的设计要求进行选择，周期太长将会导致递推器的精度降低。

2.2 故障检测原理及结构

2.2.1 故障检测原理

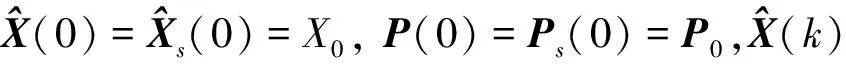
(19)

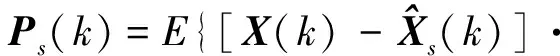
(20)

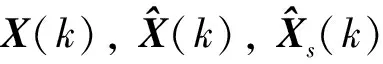
(21)

(22)

则υk的方差为：

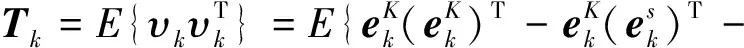
(23)

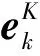
(24)

结合上述分析，只要通过对υk期望的检验即可确定系统是否存在故障。本文提出一种改进的状态χ2检测法对子系统进行故障检测，改进算法利用2个状态之间的不一致性，对子系统进行故障检测。由子系统的状态估计值和由先验信息递推计算得到的状态差值构造检验量，该检验量也是服从零均值高斯分布的随机向量，根据故障检测的统计原理[1]，即可得到故障检测函数。

2.2.2 系统故障检测

根据二元假设理论，对υk作以下二元假设：

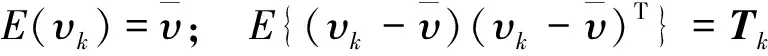
根据统计检验原理，构建故障检测函数如下：

(25)

其中,λk～χ2(n),n为状态估计X(k)的维数。

故障判定准则为：

若λk>TD，判定有故障；

若λk≤TD，判定无故障。

TD为预先设置的门限，可由误警率Pf确定。

2.2.3 故障检测结构

在一般滤波器中，初值误差、系统噪声和建模误差的影响将会由测量更新来克服，使系统的滤波精度逐渐提高，但在状态递推器中没有测量更新，所以这些误差将使状态递推值越来越偏离真值，因此无故障时υk会越来越大，方差也越来越大，降低了故障检测灵敏度。

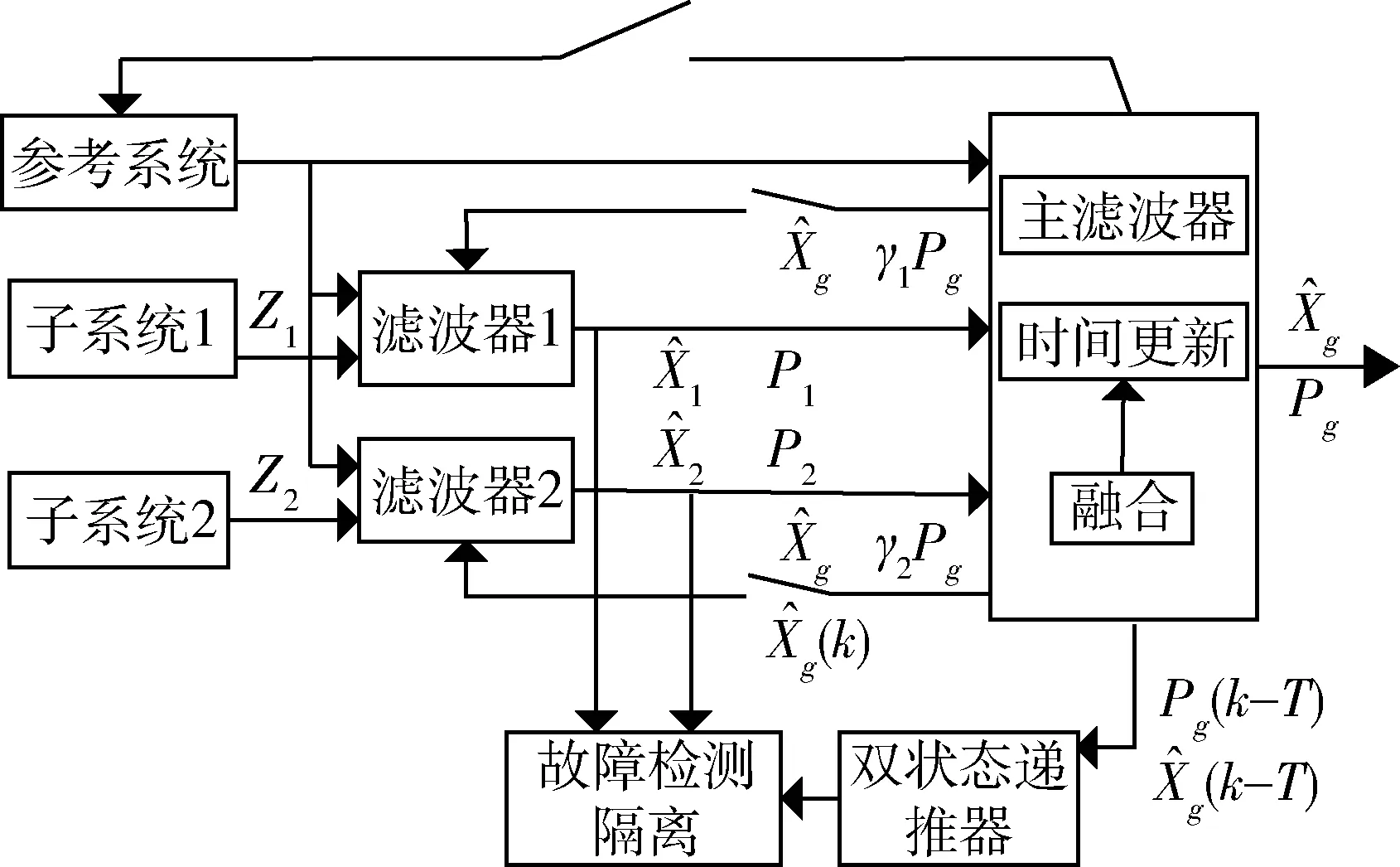
图2 改进的故障检测算法结构

与传统联邦滤波状态χ2检测法相比，可以看出，新的方法具有以下特点：

1) 由于全局融合状态估计精度高于各子滤波器，因此具有更高的故障检测灵敏度；

2) 采用双状态递推结构，使得递推器的误差不会逐渐扩大，减少了先验信息受故障污染的可能性。

3 仿真实验及分析

考虑如下非线性系统：

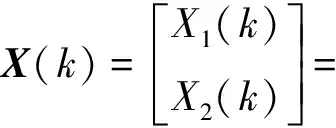
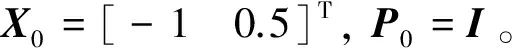
采用容积卡尔曼滤波算法对该系统进行滤波[8-9]，具体算法细节这里不再赘述，设置滤波时间为100s，取误警率Pf=0.01，则故障检测门限值TD=9.21。分别采用基于融合状态递推的检测法和传统状态χ2检测法对其进行故障检测，虚线表示状态χ2检验法，实线表示基于融合状态递推的检测方法。

假设子系统1在60s～80s之间发生突变故障，故障量为f1=6，仿真结果如图3所示。从图3中可以看出，在发生突变故障之前，2种故障检测算法函数值均低于故障检测门限值，没有出现误报现象，当系统在60s处发生突变故障后，函数值迅速增大并且超过故障检测门限值。说明2种故障检测算法此时均可以作出有效的判断，但是在68s处以及73s～77s这一时间段内，传统的故障检测算法灵敏性迅速下降甚至出现不报警的现象，而改进的故障检测函数值始终大于故障检测门限值和传统的故障检测函数值，这说明本文所提出的故障检测法具有对突变故障较高的灵敏度，优于传统故障检测算法。

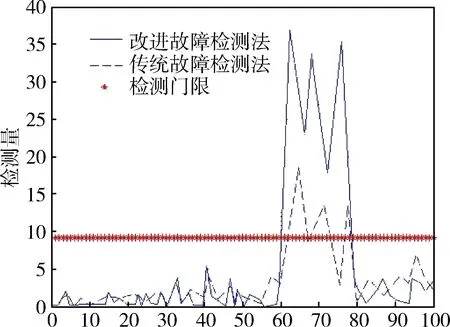
图3 突变故障检测

为了进一步检验改进故障检测算法的性能，假设系统在在60s～100s内发生缓变故障，故障量为f2=0.1×(k-60)，其余条件不变，仿真结果如图4所示。通过仿真结果可以看出，当系统出现缓变故障时，改进的故障检测算法的函数值迅速增大并始终大于传统的故障检测函数值，说明当系统出现缓变故障时，本文所提算法灵敏度始终要高于传统故障检测算法，所以当系统出现缓变故障时可以比传统检测算法更及时地检测出系统故障状态。

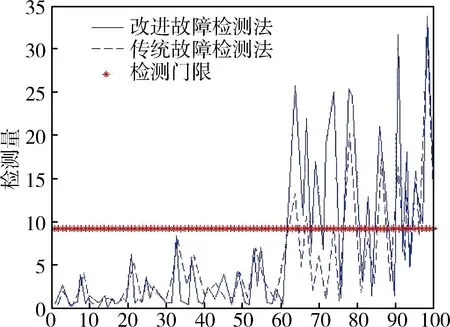
图4 缓变故障检测

4 结论

针对联邦滤波器结构的特殊性，全局最优融合状态的精度高于局部滤波值的特点，本文提出了一种改进的故障检测方法。该算法结合联邦滤波器的全局最优状态融合和状态递推器获得融合状态递推算法，再通过各子系统的非线性滤波器得到状态估计与融合状态递推器之间的残差构造故障检测函数的检验量。仿真实验结果表明，该算法对于突变故障和缓变故障均具有比传统的故障检测算法更高的检测灵敏度，验证了所提算法的有效性。

参 考 文 献

[1] 卞鸿巍,李安,覃方君,许江宁等. 现代信息融合技术在组合导航中的应用[M].北京:国防工业出版社,2010.

[2] 高运广,王仕成,刘志国, 赵欣. 一种基于LS-SVM的联邦滤波故障检测方法[J].控制与决策, 2011, 26(9): 1433-1435. (Gao Yunguang, Wang Shicheng, Liu Zhiguo, Zhao Xin. Fault Detection Method Based on LS-SVM for Federated Kalman Filter[J]. Control and Decision, 2011, 26(9): 1433-1435.)

[3] 张科,刘海鹏,李恒年,钱山. SINS/GPS/CNS组合导航联邦滤波算法[J].中国惯性技术学报, 2013, 21(2): 226-230. (Zhang Ke, Liu Haipeng, Li Hengnian, Qian Shan. SINS/GPS/CNS Integrated Navigation Federal Filtering Algorithm[J]. Journal of Chinese Inertial Technology, 2013, 21(2):226-230.)

[4] 荣军,邱恺,陈天如,吴训忠. 基于量测一致性的联邦滤波故障检测方法研究[J].传感技术学报, 2006, 19(4): 2556-2558.(Rong Jun, Qiu Kai, Chen Tianru, Wu Xunzhong. Fault Detection Method for Federated Filtering Structure Based on the Consistency Between the Measurements[J]. Chinese Journal of Sensors and Actuators, 2006, 19(4): 2556-2558.)

[5] 熊智,邵慧,华冰,等. 改进故障隔离的容错联邦滤波[J].航空学报, 2013, 36(3): 929-938. (Xiong Zhi, Shao Hui, Hua Bing, et al. An Improved Fault Tolerant Federated Filter with Fault Isolation[J]. Acta Aeronautica et Astronautuca Sinica, 2015, 36(3): 929-938.)

[6] Carlson, N.A., Federated Filter for Distributed Navigation and Tracking Applications[C], Proc. ION 58th Annual Meeting, June 2002:340-353.

[7] A. Maier, S. Kiesel, G. F. Trommer. Performance Analysis of Federated Filter for SAR/TRN/GPS/INS Integration[J]. Gyroscopy and Navigation, 2011, 2(4):293-300.

[8] Arasaratnam I, Haykin S. Cubature Kalman Filter[J]. IEEE Trans on Automatic Control, 2009, 54 (6): 1254-1269.

[9] 沈飞,郝顺义,吴训忠,郭创,杨彬. 简化平方根容积卡尔曼滤波的INS/GPS紧组合算法[J].航天控制, 2016, 34(1): 15-19. (Shen Fei, Hao Shunyi, Wu Xunzhong, Guo Chuang, Yang Bin. INS/GPS Tightly Integrated Algorithm Based on Reduced Square-Root Cubature Kalman Filter[J]. Aerospace Control, 2016, 34(1): 15-19.)