基于双幂次趋近律柔性火箭滑模变结构控制
2018-05-18于亚男王海鹰
于亚男 吴 颀 王海鹰 金 龙
上海航天控制技术研究所,上海 201109
运载火箭在飞行过程中飞行空域变化很大,其气动参数变化范围也较大,有些干扰或者参数甚至是无法确定的。飞行时,不仅内部燃料消耗、液体晃动引起的质心偏移会影响运载火箭的转动惯量,还会受到风干扰力矩等的影响。这些不确定因素对运载火箭姿态控制的影响很大,箭体弹性与主体的耦合作用以及各种不确定性的影响可能会导致运载火箭控制失效,因此要求运载火箭姿态控制算法具有较好的鲁棒性。在传统控制方法中,通常采用变增益和变网络的方法,在不考虑外界干扰和耦合的条件下在不同时间点进行频域设计,这就要求控制系统有较好的裕度,对于不同的飞行阶段,采用不同的动静态增益和校正网络。这种方法对于发射不同有效载荷的运载火箭来说,每一发都需要重新设计,设计效率低,对外界不确定干扰的鲁棒性较差。因此,自适应性和鲁棒性能较好的运载火箭姿态控制方法成为现阶段研究的热点问题。
滑模变结构控制算法是一种自适应性鲁棒性能好的控制方法,广泛应用于具有不确定特性的飞行器姿态控制算法中[2],但是传统的滑模变结构控制算法在实现控制时存在严重的抖振问题,这对控制器执行机构的性能有很高要求,实现困难[3]。国内外很多学者针对滑模变结构抖振问题提出了一些解决方法,一种方法是在滑动平面的两边引入边界层,文献[4]利用饱和函数代替符号函数达到抑制抖振的目的,但这种方法边界层厚度的值是固定的,是以减弱滑模变结构控制的鲁棒性为代价的。文献[5]提出一种具有动态边界层的饱和函数控制法,可使边界层随状态轨迹的收敛而逐渐收缩到与滑模面重合,使状态轨迹最终收敛到切换平面上。随着遗传算法等人工智能控制算法的发展,文献[6]以输入输出反馈线性化进行模型转换,采用模糊控制理论改进指数趋近律,并通过遗传算法进行控制参数优化。但这些方法中均没有具体地考虑模型不确定性和外界干扰的影响。对于柔性运载火箭这种模型较为复杂的系统,国内研究的内容较少,文献[7]针对柔性运载火箭的滑模变结构姿态控制问题提出了一种基于超螺旋算法的解决方法,超螺旋算法可以在不需要增加观测量的基础上解决滑模变结构的抖振问题,但是超螺旋算法仅适用于系统相对阶为1的问题,使用时需要有此类证明。根据文献[8]的结论,双幂次趋近律具有固定的时间收敛特性,又能有效消除滑模变结构的抖振问题,当系统存在有界集的扰动时,能保证滑模及其一阶导数有限时间内收敛到稳态误差内。
在以上研究的基础上,本文建立了具有弹性特性的运载火箭俯仰方向的小偏差数学模型,设计基于快速幂次趋近律的滑模变结构控制器,为了改善控制器的鲁棒性和抗干扰能力,提出了应用双幂次趋近律算法实现的滑模变结构控制器,最后验证了此算法的优越性。
1 运载火箭数学模型
考虑运载火箭的弹性振动,根据小偏差线性化方法将姿态动力学方程进行简化,得到的俯仰通道模型为
(1)
弹性振动方程为:
(2)
弹性振动模态被看作扰动项,将模型规范化,写成状态方程的形式为:
(3)
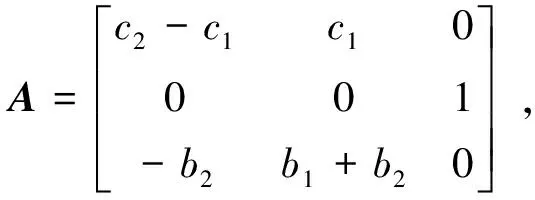
2 基于弹道倾角观测器的状态反馈控制系统设计
由于弹道倾角θ在实际的火箭飞行过程中无法精确测量,所以要通过设计状态观测器对其进行观测得到,观测器的引入使得受控系统状态反馈的物理实现成为可能。
定理:对于n维连续时间线性时不变被观测系统:
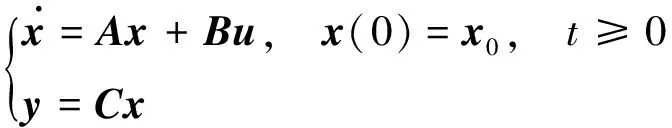
(4)
其中,A∈n×n,B∈n×p,C∈q×n,{A,C}完全能观测。那么,若系统输出矩阵C为满秩,即rankC=q,则系统降维状态观测器ΣROM的最小维数为
dimΣROM=n-q
进而,若观测系统为单输出即q=1,则降维观测器ΣROM的最小维数为n-1。若被观测系统为多输出即q>1,则降维观测器ΣROM的最小维数为n-q,则q越大ΣROM的最小维数越小,即降维观测器ΣROM结构越简单。
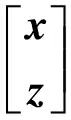
取降维观测器为n-q维降维状态观测器:
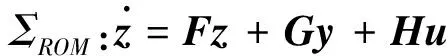
(5)
其中,(n-q)×(n-q)矩阵F的特征值可按期望要求任意配置,系数矩阵满足关系式:

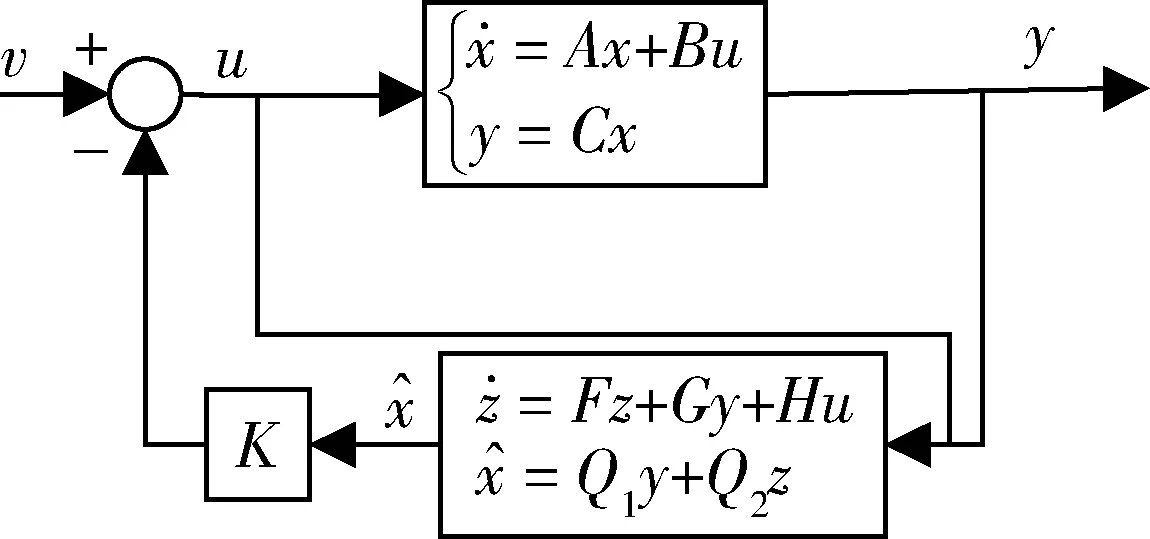
图1 基于观测器的状态反馈控制系统
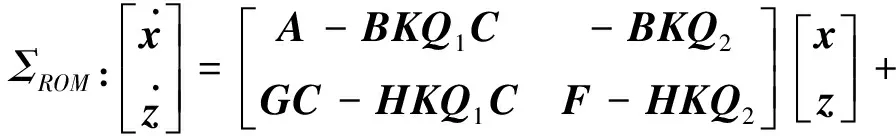
(6)

(7)
系统状态观测器的结构图如图2所示

图2 状态观测器的结构图
状态观测器的参数G=c1,F=c2-c1,H=c3。
3 运载火箭滑模变结构姿态控制
为了确保设计的滑模变结构控制具有良好的手链特性和鲁棒性,本文使用具有固定时间收敛特性的双幂次趋近律进行趋近律设计。
双幂次趋近律如下:
(8)
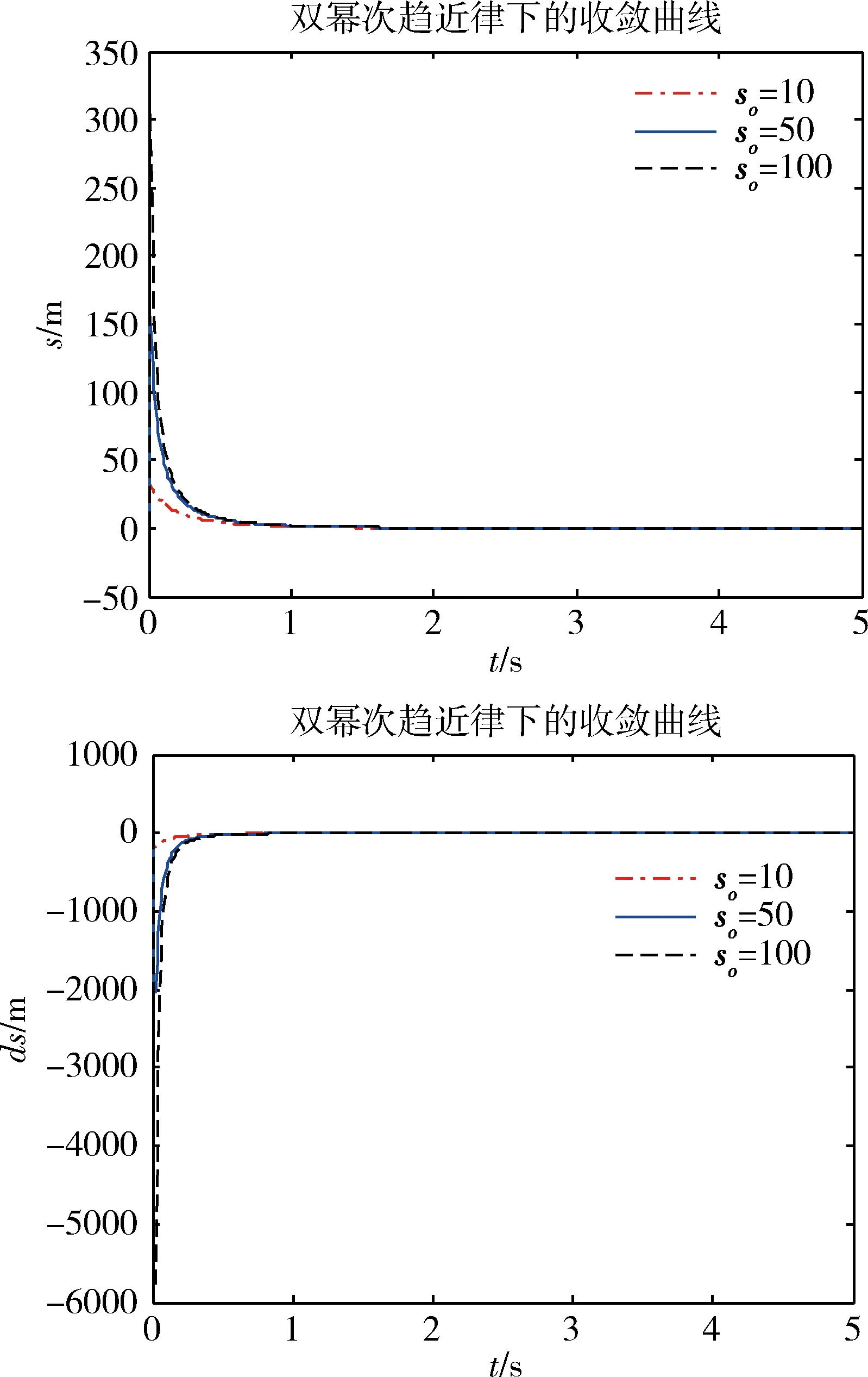
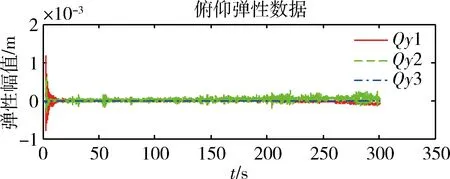
其中:k1>0,k2>0,a1>1,0 本双幂次趋近律具有固定时间收敛特性的证明: (9) (10) 证明:当s>0时,满足a1+a2=2,若双幂次趋近律可以有 方程两边同时除以sa2,则上式可以写为 令y=s1-a2,则s=y1/(1-a2),带入上式化简后得到广义的Riccati微分方程为 其通解为 由s(0)=s0可得 由上式可得,滑模初值s0仅出现在反正切函数里,由反正切函数y=arctan(x)∈[0,π/2),x≥0 因此,这类双幂次趋近律的收敛时间存在上确界Tsup,且Tsup与滑模初值s0无关。 (11) 根据双幂次趋近律的定义 (12) 根据式(11)和(12),可得 则控制变量: (13) 为了验证基于观测器双幂次趋近律的滑模变结构控制在运载火箭姿态控制上应用的有效性,应用实际动力学参数,将其控制效果和基于观测器的状态反馈控制方法进行了仿真比较。 1)不同初值条件下的收敛时间 图3 不同初值条件下双幂次趋近律s和收敛曲线 2)系统存在有界集总扰动时的控制效果 考虑运载火箭箭体3阶弹性振动模态,将弹性振动对箭体姿态运动的影响作为干扰项,箭体的俯仰方向弹性振动曲线如图4所示,将外界干扰和姿态角初值干扰作为耦合干扰项,考虑实际情况中发动机摆角限幅,设计滑模控制器控制参数,并对控制效果曲线进行仿真。 图4 弹性振动干扰曲线 图5 基于双幂次趋近律的姿态角控制效果曲线 图6 基于双幂次趋近律的发动机摆角Δδ曲线 由以上仿真分析可知:基于双幂次趋近律设计的控制器具有全局快速的固定时间收敛特性,收敛时间存在与滑模初值无关的上界。双幂次趋近律能保证滑模及其一阶导数在有限时间收敛到稳态误差界内;在控制力矩受限的条件下,基于双幂次趋近律算法的滑模变结构控制器能实现箭体柔性振动等有界集总扰动条件下的姿态稳定控制,并消除了滑模控制抖振的问题。 提出了一种基于弹道倾角观测的运载火箭滑模变结构控制器设计方法,该方法采用双幂次趋近律滑模函数,具有全局固定时间收敛特性的同时能够有效抑制变结构控制引起的高频抖振。数值仿真表明,考虑实际情况控制受限时,在箭体系统存在有界集总扰动作用下,提出的控制器表现出良好的自适应能力和鲁棒性。基于双幂次趋近律的滑模变结构算法具有全局固定时间收敛特性并解决了滑模算法高频抖振的问题,但是应用于实际系统仍存在不足,滑模控制参数选择仍采用试凑法,后续工作中考虑进一步研究滑模参数自适应的控制方法。 参 考 文 献 [1] 刘刚, 李传江, 马广富,等. 应用SGCMG的卫星姿态快速机动控制[J]. 航空学报.2011, 32(10):1905-1913.(Liu Gang, Li Chuanjiang,Ma Guangfu, et al. Time Efficient Controller Design for Satellite Attitude Maneuvers Using SGCMG[J], Acta Aeronautica ET Astronautica Sinica, 2011, 32(10): 1905-1913.) [2] Pukdeboon,C.Zinober,A.S.I. Optimal Sliding Mode Controllers for Spacecraft Attitude Manoeuvres[C]. ROCOND'09-6th IFAC Symposium on Robust Control Design, Proceedings, 2009: 173-178. [3] 高为炳. 变结构控制的理论及设计方法[M]. 北京:科学出版社,1996. [4] 席雷平,郭辉,何东.基于饱和函数的机械臂模糊滑模趋近律设计[J]. 河北科技大学学报.2011,32(5):482-487.(Xi Leiping, Guo Hui, He Dong. Design of Fuzzy Trending Law Based on Saturation Function in Sliding Mode Control for Robotic Manipulators[J]. Journal of Hebei University of Science and Technology, 2011, 32(5): 482-487.) [5] 金鸿章, 罗延明, 肖真,等. 抑制滑模抖振的新型饱和函数法研究[J]. 哈尔滨工程大学学报, 2007,28(3):288-291.(Jin Hongzhang, Luo Yanming,Xiao Zhen, et al. Investigation of A Novel Method of Saturation Function for Chattering Reduction of Sliding Mode Control[J]. Journal of Harbin Engineering University, 2007, 28(3) :288-291.) [6] 王健, 杜庆余. 基于模糊策略的高速飞行器滑模控制律设计[J]. 航天控制.2011,29(4):49-54.(Wang Jian, Du Qingyu. The Design of Sliding Mode Control Law Based on Fuzzy Strategy for Hypersonic Vehicle[J]. Aerospace Control, 2011, 29(4):49-54.) [7] 王青,王昭,董朝阳.一种基于二阶滑模的柔性运载火箭姿态控制[J]. 系统仿真学报.2009,21(7):2006-2009.(Wang Qing, Wang Zhao, Dong Chaoyang. Attitude Control of Flexible Launch Vehicles Based on Second-order Sliding Mode[J].Journal of System Simulation,2009,21(7): 2006-2009.) [8] 李慧洁, 蔡远利. 基于双幂次趋近律的滑模控制方法[J]. 控制与决策. 2016,11(3):499-502.(Li Huijie, Cai Yuanli. Sliding Mode Control with Double Power Reaching Law[J]. Control and Decision, 2016, 11(3): 499-502.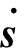
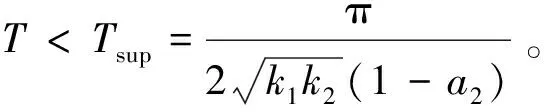
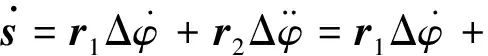
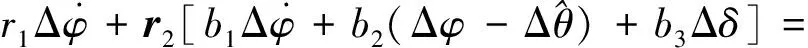
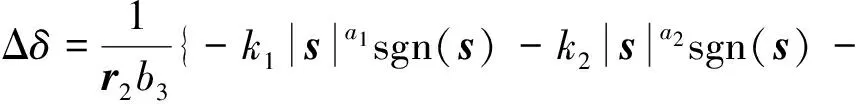
4 仿真结果
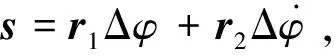
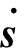
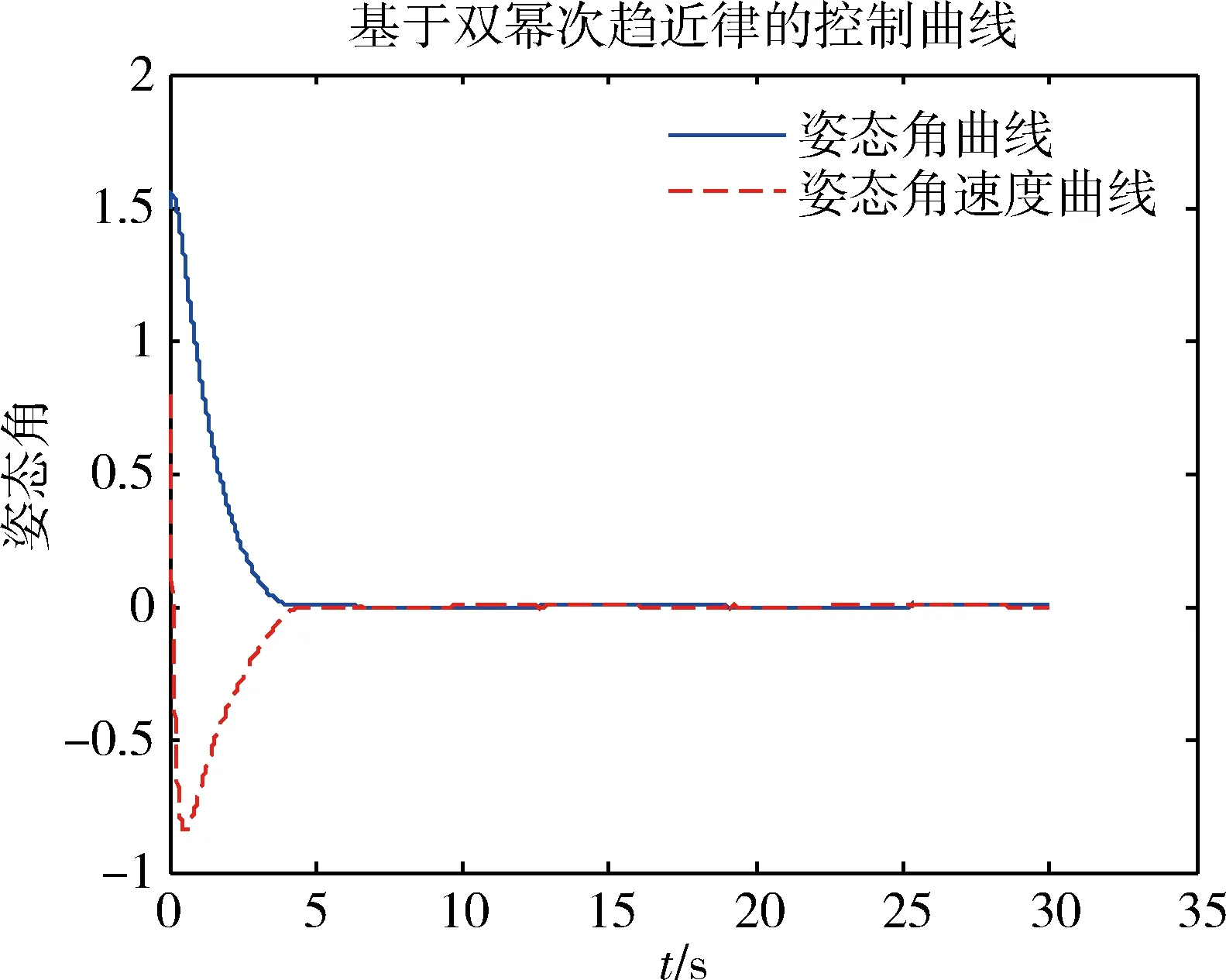
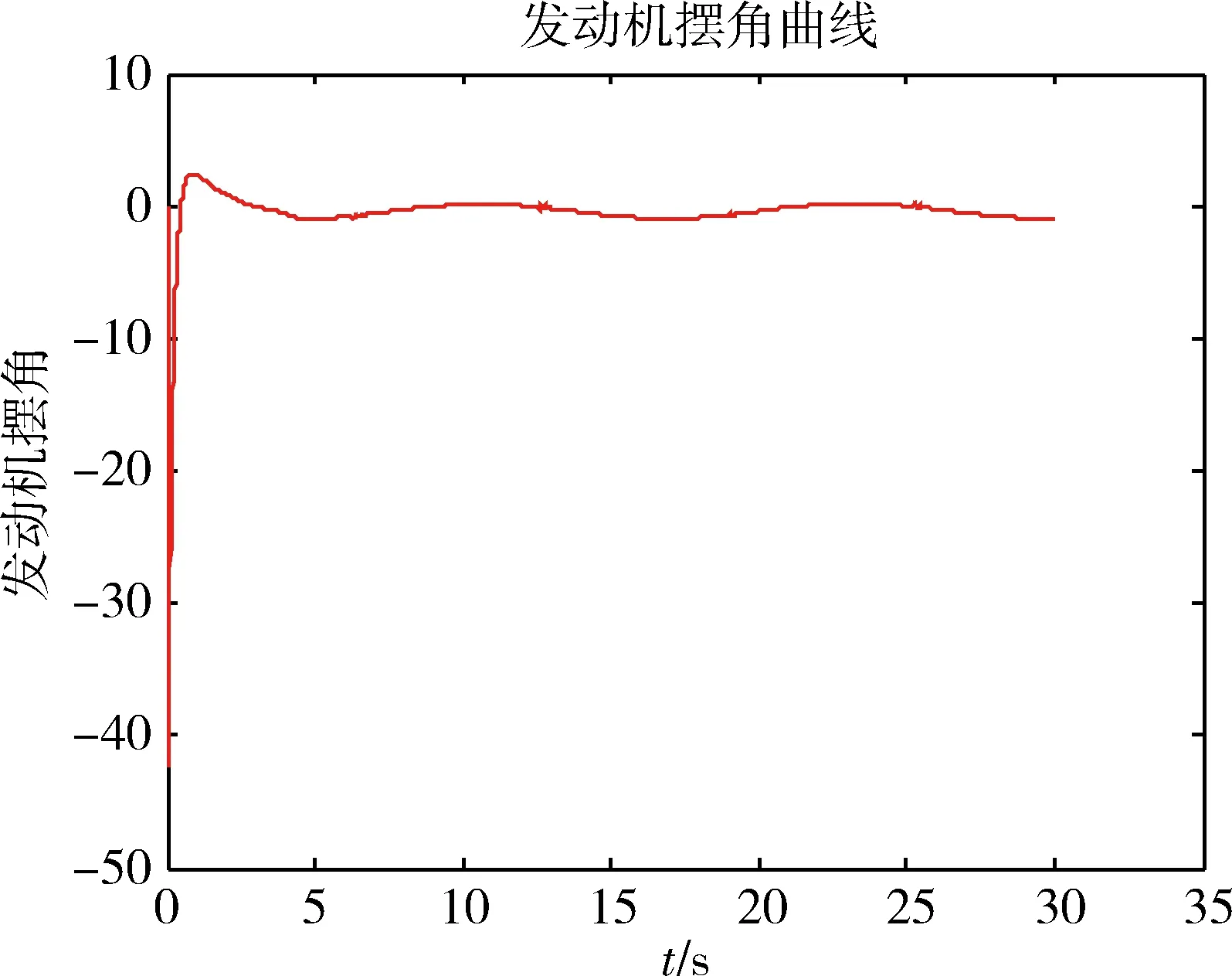
5 结论
