GPS/INS组合导航中两步自适应滤波方法*
2018-05-18易清明陆景龙
易清明 陆景龙 石 敏
暨南大学信息科学与技术学院, 广州 510632
单一的导航系统有着本身无法克服的缺点,近年来,融合多个导航系统的组合导航系统越来越受到关注,成为研究的热点领域[1-3]。全球定位系统(GPS)可以实时地提供全天候、高精度的位置和速度信息,但是在森林、多山地区、隧道和城市峡谷等场景则无法进行定位导航[2-4];惯性导航系统(INS)具有自主导航的特点,但是误差会随着时间累积,无法保证导航系统的准确性[1,4-5]。GPS观测值可以抑制INS系统的漂移,而INS系统则对GPS导航结果进行了平滑并补偿信号中断,GPS/INS组合导航系统结合2种技术优势,提供连续、高带宽和高精度完整的导航信息[4-6]。卡尔曼滤波器在GPS/INS组合导航系统中得到广泛应用,在系统模型确定的情况下,利用贝叶斯估计理论以及迭代理论可以得到最小均方误差(MMSE)意义下的最优滤波效果。然而,有时无法获取精确的实际模型或受到多种因素的干扰导致观测噪声不确定,这将影响参数估计的精度和可靠性,甚至导致滤波结果发散[1,3,6]。解决系统模型不确定、噪声干扰等问题的一个有效途径是采用自适应滤波技术[1,7-10]。
针对以上问题,文献[8]提出了基于贝叶斯方差估计的自适应算法,文献[10-14]提出自适应渐消滤波算法,文献[15]提出抗粗差自适应滤波。文献[5,16-20]提出基于信息估计的自适应算法,但是当误差矩阵以及测量矩阵均未知时,导致结果不确定。对此,文献[1,7]提出多模型自适应算法,文献[13-14]基于遗传学自适应算法,可以进一步解决以上问题,但是计算量巨大,建立模型过程复杂。
渐消卡尔曼滤波器通过渐消因子减少过去噪声与当前噪声的相关性,对不确定的模型也能进行很好的滤波[6-9]。在噪声干扰少、匹配性好的情况下,渐消因子的“渐消”速度慢,否则,“渐消”速度加快[1,4,20]。自适应卡尔曼滤波器通过自适应因子调整增益[5,10-14]。为了减少外界噪声以及模型不确定性,需要同时调整渐消因子和自适应因子。由于是单一因子只能进行整体调整,无法精确调整各个通道,使调整结果不精确[1-5,16-18]。
本论文提出一种2步自适应滤波算法:1)构造多重渐消因子减少对过去信息的记忆长度,同时保证误差协方差的对称性;2)利用多重自适应因子精确调整通道增益,降低噪声干扰,克服系统模型不确定的影响。多重自适应因子和多重渐消因子可以限制滤波器的记忆长度,增加当前观测数据权重,对各个通道进行精确调整,其中关键问题是多重因子的定义。
1 卡尔曼滤波器系统模型
卡尔曼滤波是导航系统中大多数状态估计算法的基础。卡尔曼滤波器之所以能够获得最小均方误差(MMSE)意义下的最优滤波效果,关键是对实际系统建立合理、准确的模型。
卡尔曼滤波器在得到有效信息后,利用系统参数的确定特性和统计特性等先验知识及观测结果来获得最优估计。在提供初始值的基础上,用先验值和最新观测数据中得到的新值的加权平均更新状态估计[6]。首先,介绍系统状态方程和观测方程。
系统状态方程表示为[7]:
Xk=Φk,k-1Xk-1+wk
(1)
观测方程表示为:
Zk=HkXk+vk
(2)
式中,Xk∈Rn是被估计状态向量;Φk,k-1∈Rn×n是k-1到k时刻的一步状态转移矩阵;Zk∈Rm是观测向量;Hk∈Rm×n是观测矩阵;wk和vk分别是系统噪声和观测噪声,均为零均值白噪声,其协方差分别是Qk和Rk;其中要求Xk,wk和vk三者互不相关。
接下来,介绍标准卡尔曼滤波器递推方程[6],式(3)~(7)不仅描述了卡尔曼滤波递推公式,同时也描述滤波器的工作流程。
Xk,k-1=Φk,k-1Xk-1,k-1
(3)
(4)
(5)
Xk,k=Xk,k-1+Kk(Zk-HkXk,k-1)
(6)
Pk,k=(I-KkHk)Pk,k-1
(7)
式中,Pk是Xk的协方差矩阵,在GPS/INS组合系统中则为误差协方差矩阵,对角线元素为各个状态的方差,非对角元素表示不同状态估计误差之间的相关性;I是单位矩阵;Kk是增益矩阵,它的大小体现了实际的观测数据在估计中的作用。当已知初值X0和P0,再利用k时刻的观测值Zk进行更新,就可以得到k时刻的系统状态向量Xk[5-8]。
2 两种单因子自适应滤波器
自适应卡尔曼滤波器跟踪参数变化而进行相应的动态调整,被视为解决模型不确定的一种主要途径。这里介绍2种主要的自适应卡尔曼滤波器。
2.1 渐消卡尔曼滤波
渐消卡尔曼滤波器与标准卡尔曼滤波器的不同在于引入渐消因子λk,增加新数据在迭代中的作用,减少旧数据的权重。其误差协方差变成如下形式[5-9]:
(8)
基于残差定义一步最佳渐消因子λk如下[8-10]:
γk=Zk-HkXk,k-1
(9)
(10)
(11)
(12)
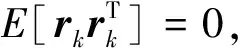
渐消因子λk的作用是减少观测值对递推过程中系统建模不确定性和噪声特性未知对滤波的影响。当残差γk误差增大时,引起残差序列自协方差增大,渐消因子λk相应增大,抑制噪声影响,以抑制滤波发散[7-10]。
2.2 自适应增益滤波器
在传统卡尔曼滤波中存在2点不足:1)缺少冗余观测信息时,导致卡尔曼滤波的稳定性和效率下降,误差增大;2)观测卫星数少于4颗时,无法用GPS系统纠正INS的精度。针对这2个问题,引入自适应因子。
引入自适应因子αk(0<αk≤1)后的增益方程,变成如下形式:
(13)
自适应因子αk有2种确定方法:基于预测状态和基于残差。基于残差的方法更适合在GPS/INS松耦合系统中使用,因此,文中采用基于残差的方法确定自适应因子αk:
(14)
(15)
(16)
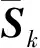
3 两步自适应滤波算法
通过上节分析可知,单一渐消因子和自适应因子可以降低噪声的干扰,但是只能进行整体调整,不能精确滤波[15-17],这里提出一种改进的自适应滤波算法,即两步自适应滤波算法。在GPS/INS组合系统中,状态变量Xk是一组多维向量矩阵,含有多个状态变量,当存在外界噪声干扰时,需要一个因子矩阵进行逐个精确调整,即λk和αk都应该是一个因子矩阵,但按上述方法,λk和αk实际上是一个数值,只对整个协方差矩阵Pk和增益矩阵Kk进行整体调整,并没有对各个通道进行调整,导致调整效果不佳。为此,论文引入多重因子,它可以精确调整各个通道,而不是平均调整。其中关键是多重渐消因子和自适应因子的定义。
两步自适应滤波算法的基本思想是:第1步利用多重渐消因子抑制噪声,减少记忆长度,减少噪声相关性,减少模型偏差;第2步利用多重增益因子调整卡尔曼增益矩阵,优化滤波结果。
3.1 多重渐消因子定义
把状态预测协方差矩阵Pk,k-1写成如下形式:
(17)
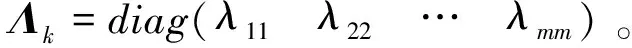
把式(17)带入式(15)中,得到:
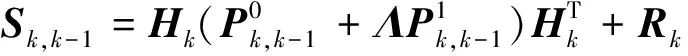
(18)
以Λ为优化变量,采用Frobenius范数的平方表示代价函数,如下:
(19)
(20)
其中,
(21)
式(21)对Λk进行微分,考虑到β为反对称矩阵,有:
(22)
求取代价函数J(Λ)的最小值,则有:
(23)
由于多重渐消因子Λk为对角矩阵,联合式(21)和式(23),得到:
(24)
由于仅对误差协方差矩阵的对角元素进行加权,其仍然满足MMSE准则,因此仍然有MMSE条件下的最优解。不论是单一渐消因子还是多重渐消因子都是依据残差定义[16-17],单一因子仅能对整体进行平均调整,而多重自适应因子可以精确调整各个通道的权重,可以获得精确的滤波效果。
3.2 多重自适应因子定义
引入多重自适应因子后,式(13)变为如下形式:
(25)
在k时刻的多重自适应因子αk为对角矩阵,表示为:
(26)
推广式(14)~(16)的自适应因子的定义,可以得到多重自适应因子的定义:
(27)
(28)
diag(·)是对角矩阵,对于矩阵而言,diag(·)即把矩阵主对角元素构成对角矩阵;di为Dk对角矩阵上的第i个元素。
基于残差定义的多重自适应因子可以直接对增益矩阵进行多通道、精确调整,降低噪声的干扰,增加真实观测对滤波器的调整作用,避免使用多个平行卡尔曼滤波器。
依据残差进行定义的多重自适应因子,可以满足调整各通道增益的需求。当存在粗差时,第1步多重渐消因子可以减少粗差干扰,降低观测异常的影响,修正模型;第2步多重自适应因子调整卡尔曼滤波增益,降低噪声影响,滤波效果得到提高[14-15]。
4 实验及分析
为了验证算法,GPS/INS组合导航系统采用松耦合方式。松耦合方式采用速度、位置的组合形式,以GPS的位置和速度作为参考值,以INS和GPS系统的位置和速度差值作为观测值,由于结构简单,工程易于实现,因此获得广泛使用。
4.1 实验环境介绍
组合导航系统安装在一台测试车辆上,如图1所示,图1中的图a为搭载组合系统车辆的示意图,b为组合系统平台,固定在车上的实验台上,c为GPS接收机,它的天线安装在车顶部(保证能搜到4颗星),d表示INS固定在实验台底部,与车辆相对静止,Y轴指向车前进方向,Z轴正方向指向天向,根据右手法则确定Y轴,如图1(a)所示。
图2 部分车辆测试路线
测试车辆在广州天河区进行道路测试,以北纬22.7°,东经113.6°为起点,行驶1h,回到起点,部分测试路线如图2所示。由于数据量巨大,为了减少数据量,提高处理速度,截取60s的一段数据,包括直线和90°转弯。获取的数据在MATLAB 12.0环境下进行仿真验证。平台硬件采用加拿大NovAtel公司基于OEM6的LCI系列产品,它采用SPAN技术,可以获得连续的速度、位置、姿态信息,满足高精度、高稳定性的需求,表1给出INS的主要技术参数。

表1 INS的主要技术参数
4.2 实验结果及分析
这里给出标准卡尔曼滤波器与3种自适应卡尔曼滤波器的对比:渐消卡尔曼滤波器,常规自适应卡尔曼滤波器以及改进后的自适应卡尔曼滤波器。
值得注意的是,论文中采用松耦合的组合导航直接获取的观测数据为位置和速度,滤波效果对位置、速度反映灵敏,在姿态上则不明显。由于论文篇幅受限,这里以北、东及地速度误差结果对比进行说明。
图3~5分别为4种算法在北、东、地方向上的速度误差对比。实验模拟路线既有直线路段,也有90°转弯,覆盖实际路况。在开始的2s内,由于滤波器还无法进行跟踪,因此出现从负值大幅度跳动到正值的情况,之后则正常跟踪。
从图3~4的仿真结果可以看出,原始卡尔曼滤波出现1个较大上下波动,1个较低的波谷以及2个较高的波峰,渐消卡尔曼滤波器和自适应滤波器相对原始卡尔曼滤波的波动小,在车辆速度变化时,波动较小,在波峰波谷部分有明显改进,说明这2种算法可以较好地抑制噪声干扰。改进的自适应算法的跟踪性最好,误差波动更小,尤其在图4的东向速度分量中可以看出。改进的自适应算法分2步进行滤波,并且以多重因子代替单因子,可以较好地抑制噪声,实现动态增益,滤波效果得到较好的改进,速度误差波动较小,跟踪性能较强,收敛趋势更加迅速,稳定性得到提高。图4是在地向速度误差对比,3种方法都对原始滤波有优化,但是由于没有高度计辅助观测,原始数据误差较大,优化效果差别不是很明显。当路线长度增加,相应数据增加或存在粗差时,多重因子可以控制各个通道进行精确滤波,提高滤波器的稳定性和可靠性。

图3 北向误差对比
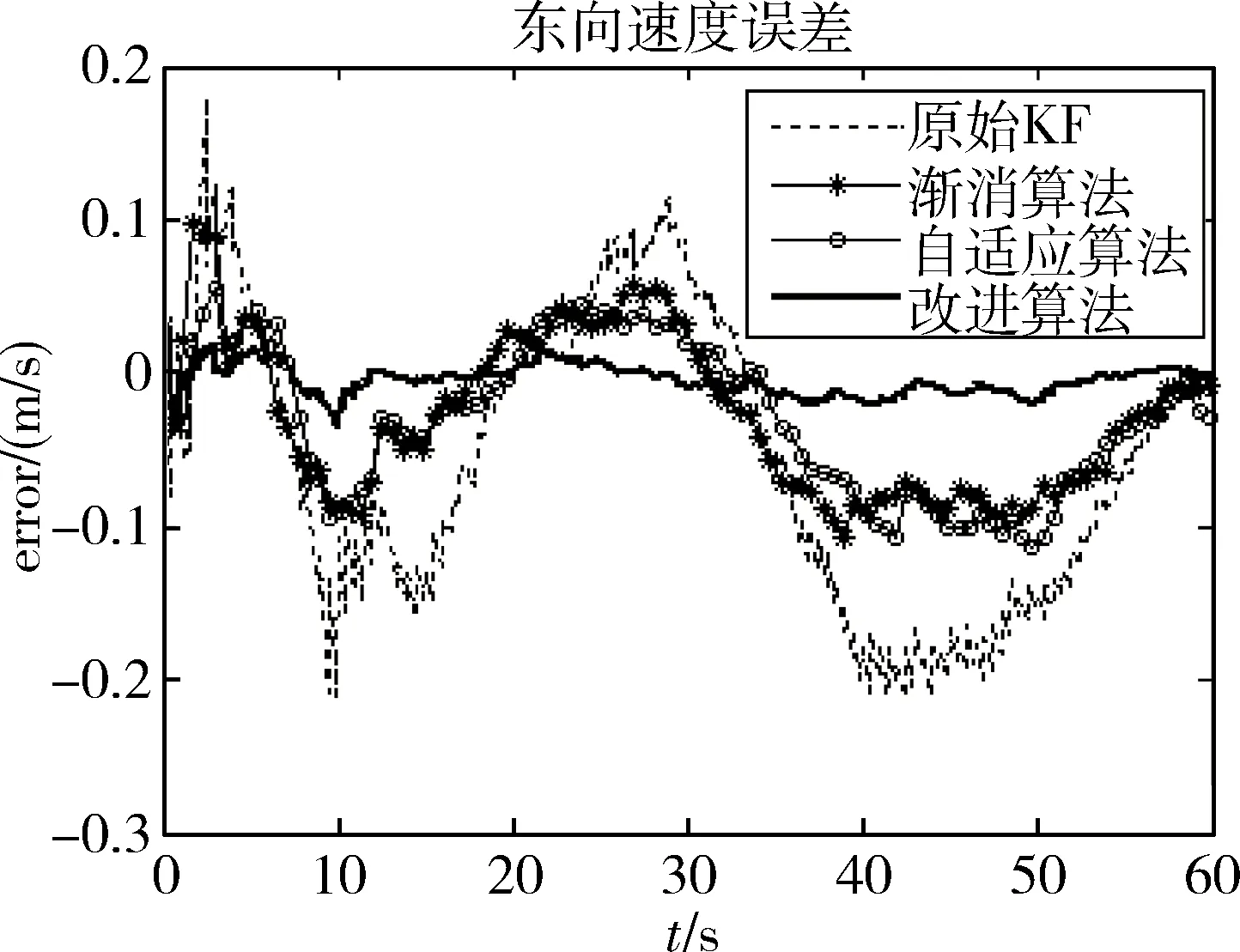
图4 东向误差对比
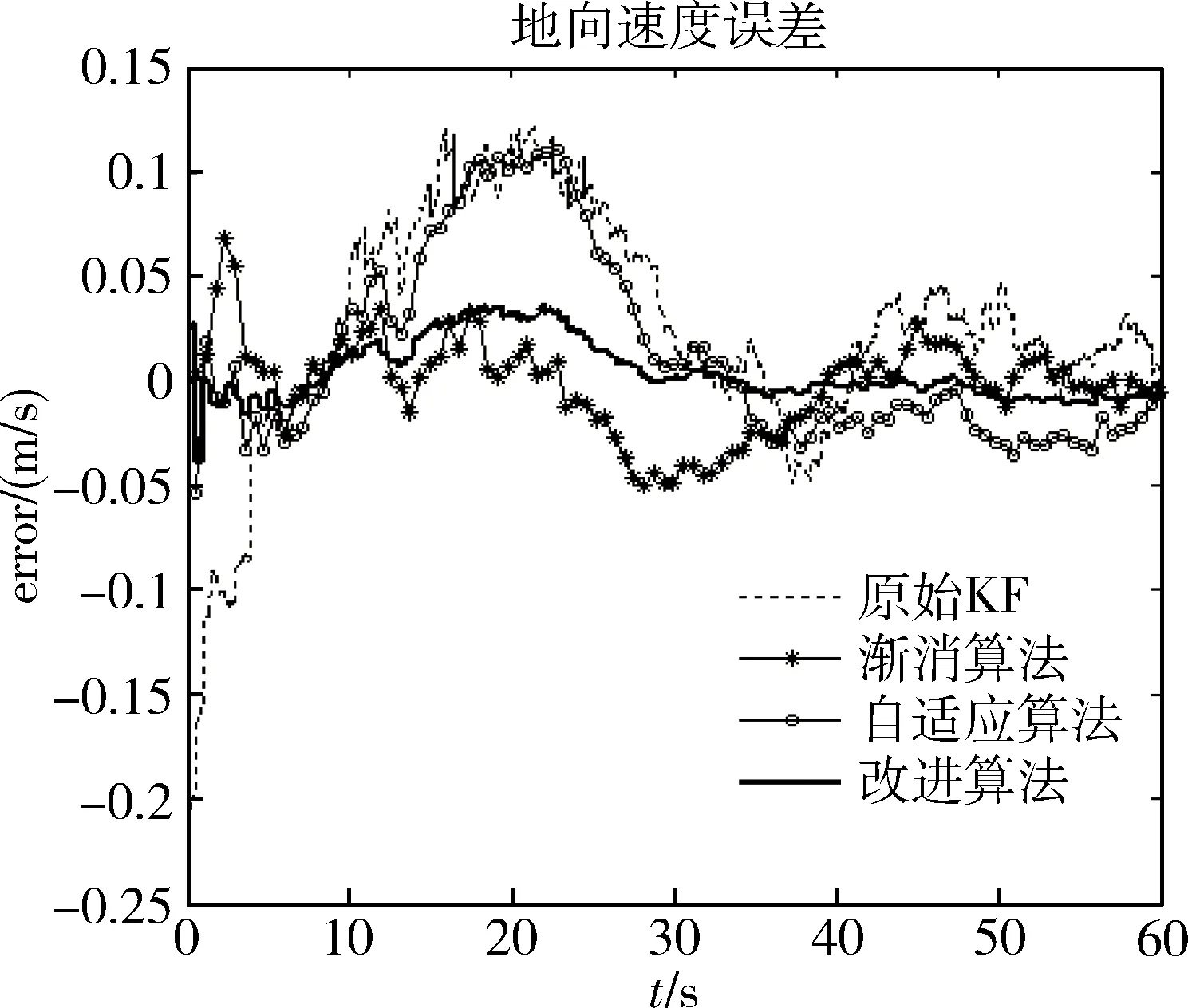
图5 地向误差对比
5 结论
单因子的渐消卡尔曼滤波器和自适应卡尔曼滤波器可以部分解决噪声模型抖动和偏差问题,但只能进行整体、平均调整,不能精确调整各个通道。本论文提出的2步自适应卡尔曼滤波算法,构造基于残差协方差估计的多重渐消因子和自适应因子,精确调整误差协方差矩阵和增益矩阵的各个通道,克服动态环境下跟踪性差的局限性。实验和仿真结果表明,改进后的自适应卡尔曼滤波算法可以精确调整各通道,增强系统的定位精度和鲁棒性、多变量跟踪能力,对算法改进以及实际应用有一定指导意义。
参 考 文 献
[1] Gao Weixi, Miao Lingjuan, Ni Maolin. Multiple Fading Factors Kalman Filter for SINS Static Alignment Application[J]. Chinese Journal of Aeronautics, 2011,4: 476-483.
[2] Mohammad A K J, Mamoun F A H. Enhanced, Delay Dependent, Intellignen Fusion for INS/GPS Navigation Systemt[J]. IEEE Sensors Journal, 2014, 14(5): 1545-1554.
[3] 周卫东,乔相伟,吉宇人,等.基于残差和残差的自适应UKF算法[J].宇航学报,2010,31(7): 1798-1804.(Zhou Weidong, Qiao Xiangwei , Ji Yuren, et al. An Innovation and Residual-Based Adaptive UKF Algorithm[J]. Journal of Astronautics, 2010,31(7): 1798-1804).
[4] Zhou Yang, Wu Panlong, Li Xingxiu, et al. A New Adaptive Extended Kalman Filter for Cooperative Localization[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017:1-14.
[5] Liu Yahui, Fan Xiaoqian, Lv Chen, Wu Jian, et al. An Innovative Information Fusion Method with Adaptive Kalman Filter for Integrated INS/GPS Navigation of Autonomous Vehicles[J]. Mechanical Systems and Signal Processing,2017,100:605-616.
[6] 杨元喜,任夏,许艳等.自适应抗差滤波理论及应用的主要进展[J].导航定位学报,2013,(1):9-15. (Yang Yuanxi, Ren Xia, Xu Yan, et al. Main Progress of Adaptively Robust Filter with Applications in Navigation[J]. Journal of Navigation and Positioning, 2013, (1): 9-15.)
[7] Gao Bingbing, Gao Shesheng, Zhong Yongmin, et al. Interacting Multiple Model Estimation-based Adaptive Robust Unscented Kalman Filter[J]. International Journal of Control, Automation and Systems, 2017, 15(5):2013-2025.
[8] Wang Shiyuan, Chao Yin, Duan Shukai, et al. A Modified Variational Bayesian Noise Adaptive Kalman Filter[J]. 2017,36(10): 4260-4277.
[9] Chen Jie, Song Jian, Li Liang, et al. UKF-based Adaptive Variable Structure Observer for Vehicle Sideslip with Dynamic Correction[J]. IET Control Theory & Applications, 2016, 10(14): 1641 - 1652.
[10] Roozbeh D, Mohammad S E, Edward R D. Intrinsically Bayesian Robust Kalman Filter: An Innovation Process Approach[J]. IEEE Transactions on Signal Processing, 2017, 65(10): 2531 - 2546.
[11] Bao J L, Gu Y L, Hsu L T, et al. Vehicle Self-localization using 3D Building Map and Stereo Camera[J]. Intelligent Vehicles Symposium (IV), 2016, 927 - 932.
[12] Kaiser S. A., Christianson A. J., Narayanan R. M.. Global Positioning System Processing Methods for GPS Passive Coherent Location [J]. IET Radar, Sonar & Navigation 2017, 11(9): 1406 - 1416.
[13] 谭兴龙,王坚,赵长胜.神经网络辅助的GPS/INS组合导航自适应UKF算法[J].测绘学报, 2015,44(4):384-392.(Tan Xinglong, Wang Jian, Zhao Changsheng. Neural Network Aided Adaptive UKF Algorithm for GPS/INS Integration Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2015,44(4):384-392.)
[14] Miao Zhiyong, Shi Hongyang, Zhang Yi, et al.Neural Network-aided Variational Bayesian Adaptive Cubature Kalman Filtering for Nonlinear State Estimation[J].
[15] Huang Fuyi, Zhang Jiashu, Zhang Sheng. Maximum Versoria Criterion-Based Robust Adaptive Filtering Algorithm[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2017, 64(10): 1252 - 1256.
[16] 马龙,李晓明.基于GPS/INS组合导航的改进自适应渐消卡尔曼滤波算法[J]. 科学技术与工程, 2013, 13(33):9973-9977. (Ma Long, Li Xiaoming. Improved Algorithm of Adaptive Fading Kalman Based on GPS/INS Integrated Navigation[J].Science Technology and Engineering, 2013,13(33): 9973-9977.)
[17] 薛海建,郭晓松,周召发.基于自适应多重渐消因子卡尔曼滤波的SINS初始对准方法[J].系统工程与电子技术, 2017,(3):620-626. ( Xue Haijian, Guo Xiaosong, Zhou Zhaofa. SINS Initial Alignment Method Based on Adaptive Multiple Fading Factors Kalman Filter[J]. Systems Engineering and Electronics Technology, 2017, 39(3):620-626.)
[18] Deng Fang, Chen Jie, Chen Chen. Adaptive Unscented Kalman Filter for Parameter and State Estimation of Nonlinear High-speed Objects[J]. Journal of Systems Engineering and Electronics,2013, 24(4): 655-665.
[19] 胡高歌,高社生,赵岩.一种新的自适应UKF算法及其在组合导航中的应用[J].中国惯性技术学报,2014,22(3):357-362. (Hu Gaoge, Gao Shesheng, Zhao Yan. Novel Adaptive UKF and Its Application in Integrated Navigation[J]. Journal of Chinese Inertial Technology, 2014,22(3):357-362.)
[20] Yu M. J..INS/GPS Integration System Using Adaptive Filter for Estimating Measurement Noise Variance[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012,48(2):1786-1792.
