基于最优控制解析解的直接入轨自适应制导律

王 智 李佳峰 张 婕 王 鹏 李 强

北京宇航系统工程研究所,北京 100076

随着空间发射任务的复杂多样化，传统制导方法在满足飞行器的灵活性、机动性及高入轨要求方面显得力不从心，需要研究制导精度更高、自适应能力更强和计算实时性更好的制导方法[1]。

在直接入轨飞行器主动段运动过程中，从当前位置飞至入轨点的轨迹不止一条，但总期望飞行器能以某种最优的轨迹入轨。因此，直接入轨飞行器的制导问题就是一个以满足入轨条件为约束、以入轨速度最大为性能指标的最优控制问题[2-5]。

本文基于最优控制理论，根据直接入轨飞行器的运动特点，在采取一些有益假设的基础上，得到了直接入轨飞行器的一种基于最优控制理论的显式解析制导律。

1 主动段运动模型

飞行器第二级及其以上的各级已处于稀薄大气层中飞行，此时的空气动力对飞行程序角选择的影响可以忽略不计。

在发射坐标系建立运动方程，并认为地球扁率及其自转角速度对主动段终点运动参数的影响甚微，则其运动方程为[6-7]

(1)

式中，x,y为位置分量；vx,vy为速度分量；P为发动机推力；m为飞行器质量；φ为俯仰角；r为地心到飞行器质心的距离；fM为地球引力常数与地球质量的乘积；R为地球半径；v为飞行器速度大小；θ为弹道倾角。

2 最优控制模型

由主动段运动模型可以看出，大气层外直接入轨飞行器的制导问题是一个寻找最优推力方向、在满足入轨约束的同时以最大速度入轨的最优控制问题[8-11]。

令

u=sinφ

(2)

则有

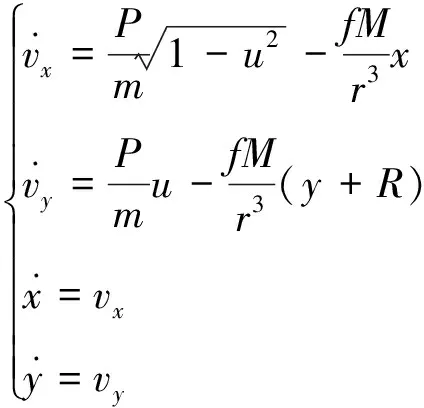
(3)

因此，直接入轨飞行器的多约束控制问题转化为在法向速度和高度满足一定约束情况下的切向速度最大问题，即

(4)

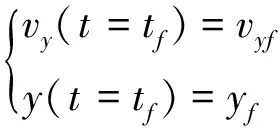
(5)

3 最优控制模型的解析解

3.1 模型简化

为得到大气层外直接入轨飞行器基于最优控制制导律的解析解，需要对运动模型进行一些简化处理[12-16]。认为飞行器所受推力为常数、地球引力场为平行而均匀的不变引力场时，则相应的简化运动模型为

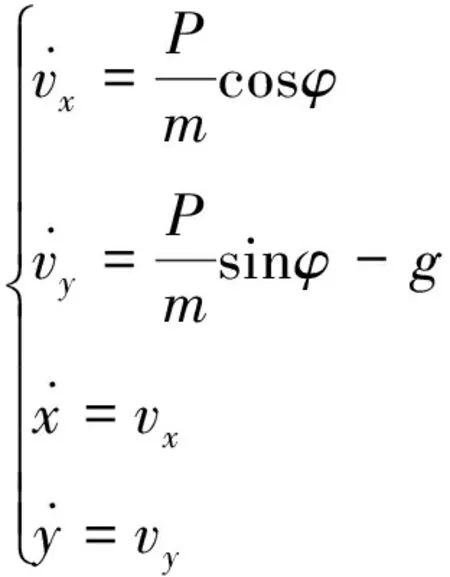
(6)

式中，g为引力加速度。

3.2 基于最优控制的显式制导解析解

对于飞行器法向运动，根据状态方程有

(7)

(8)

式中，tgo=tf-t0为剩余工作时间。

式(8)是一对联立的线性积分方程组，理论上有无穷多个解。在性能指标J的约束下，存在唯一解。定义函数

(9)

式中，c1,c2为常量，p1(t)和p2(t)为线性无关的函数。

根据式(7)和(9)，选择p1(t)和p2(t)为如下线性无关的可积函数

(10)

则有

(11)

令

(12)

则有

(13)

于是可得

(14)

式中

则有

(15)

式中

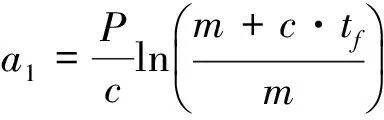
由式(14)，可得到攻角指令的解析解为

α=asin(u)-θ=asin(c1)-θ

(16)

同时，攻角指令需满足如下幅值和变化率约束

(17)

4 仿真验证

为了验证所提制导方法的有效性和鲁棒性，首先基于偏差极限组合的偏差轨迹进行仿真计算，接着进行蒙特卡洛打靶仿真。

偏差轨迹仿真结果见图1～4。从仿真结果可以看出，所提制导方法均能满足终端高度和倾角要求，验证了所提制导方法的有效性。

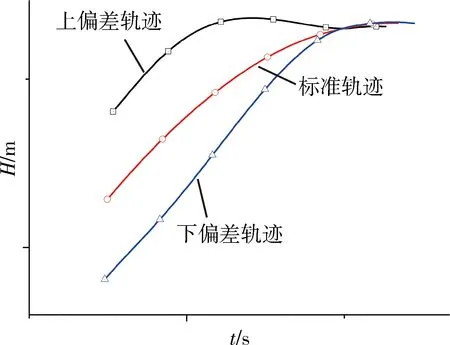
图1 飞行高度随时间变化曲线

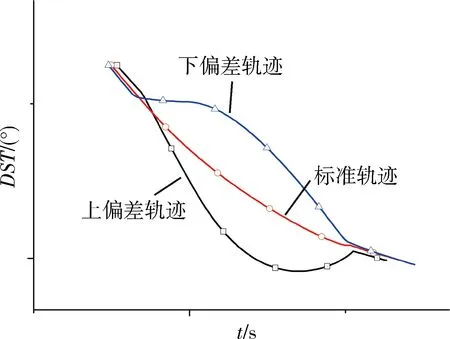
图3 当地弹道倾角随时间变化曲线

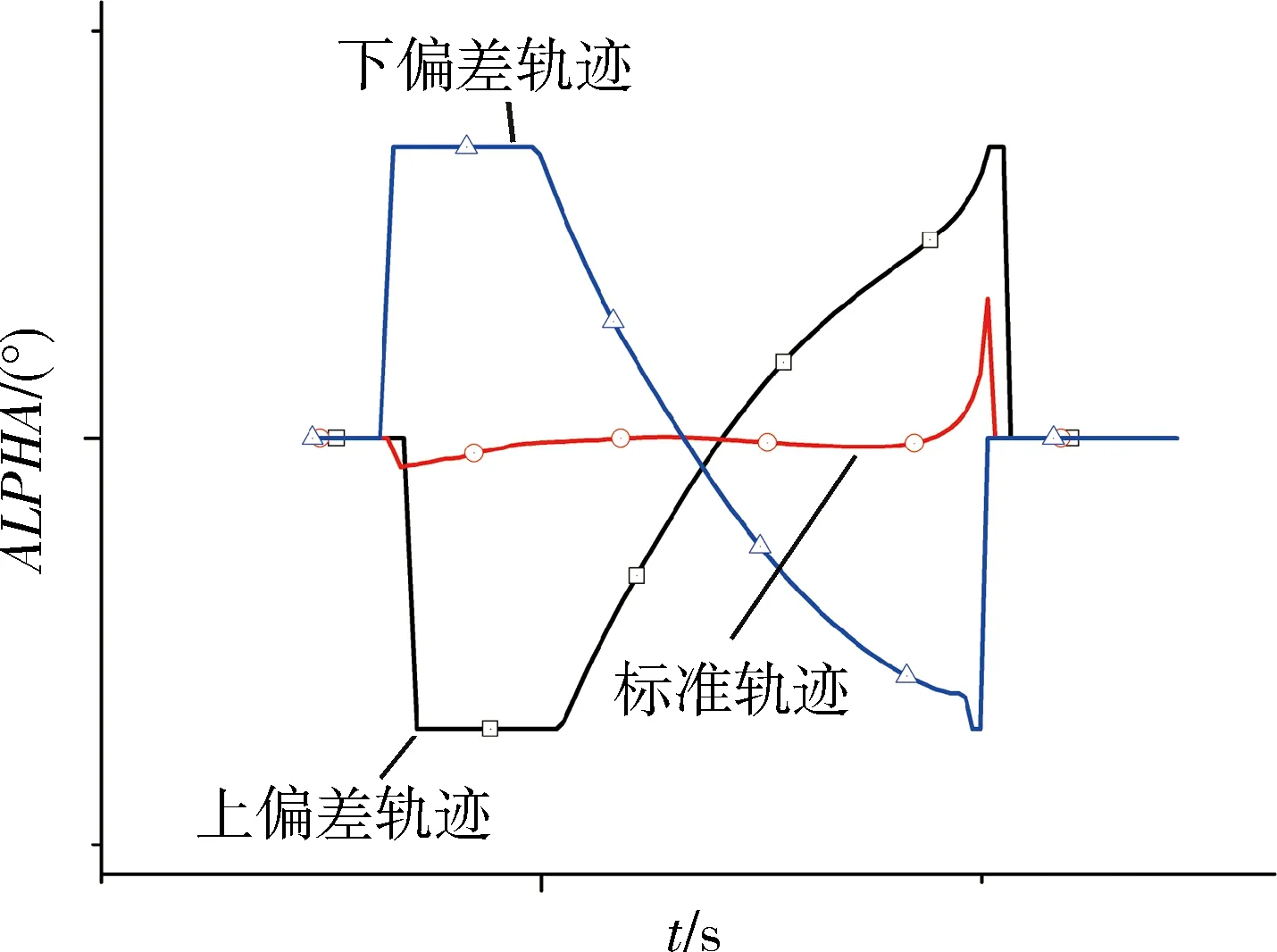
图4 攻角随时间变化曲线

2000次蒙特卡洛打靶结果见图5～7，入轨终端参数对应的标准差统计结果见表1。

图6 终端速度散布情况

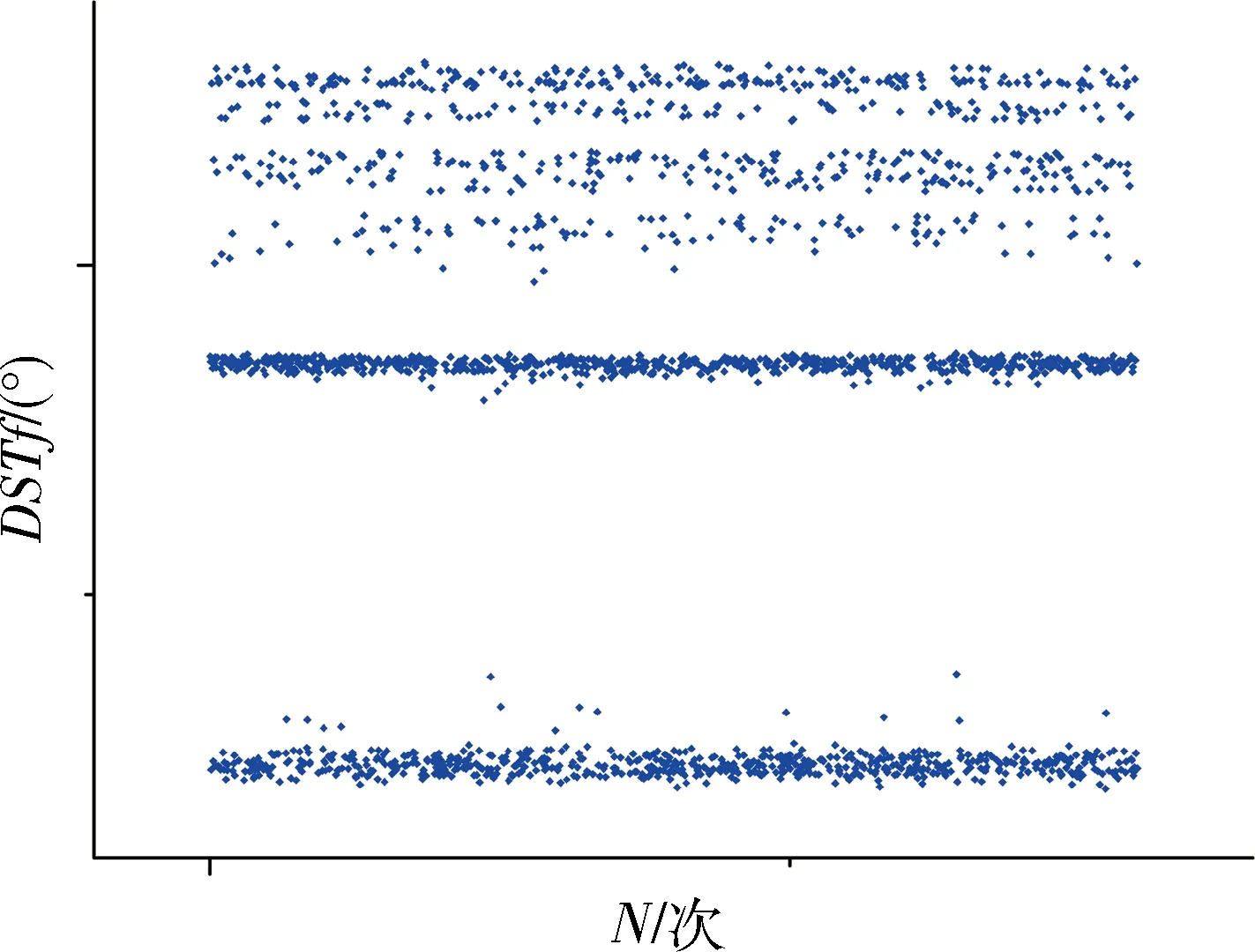
图7 终端当地弹道倾角散布情况

项目单位标准差高度m38速度m/s43当地弹道倾角(°)0．2

从图5～7和表1可以看出，所提制导方法对偏差有较好的控制作用，具有较好的鲁棒性。

5 结论

基于最优控制理论，根据直接入轨飞行器的运动特点，在采取一些有益假设的基础上，得到了直接入轨飞行器一种基于最优控制理论的显式解析制导律，并进行了相应的仿真验证，获得以下结论：

1) 该制导方法能够适应大的偏差范围，实现直接入轨飞行器的高精度入轨；

2) 制导方法基于解析解，适应性较强，计算量小，易于实现，具有较好的工程应用价值。

参 考 文 献

[1] Hanson J M, Shrader M W, Cruzen C A. Ascent Guidance Comparisons[J]. The Journal of the Astronautical Science,1995, 43(3): 307-326.

[2] Dukeman G A. Atmospheric Ascent Guidance for Rocket Powered Launch Vehicles[R]. AIAA-2002-4559, 2002.

[3] Lu P, Sun H S, Tsai B. Closed-loop Endo-atmospheric Ascent Guidance[J]. Journal of Guidance, Control, and Dynamics, 2003,26(2):283-294.

[4] Lu P, Zhang L J, Sun H S. Ascent Guidance for Responsive Launch: A Fixed Point Approach[R]. AIAA-2005-6453, 2005.

[5] Cherry G W. A General, Explicit, Optimizing Guidance Law for Rocket-propelled Spaceflight[C]. Proceeding of the AIAA/ION Astrodynamics Guidance and Control Conference. New York: American Institute of Aeronautics and Astronautics,1964: 1-32.

[6] 贾沛然,陈克俊,何力.远程火箭弹道学[M]. 长沙: 国防科技大学出版社,1993.(Jia Peiran ,Chen Kejun, He Li. Long Range Rocket Ballistics[M]. Changsha:National Defense University Press. 1993.)

[7] 张嵩.固体运载火箭弹道设计与优化[J].固体火箭技术, 1997,20(1):1-5.(Zhang Song. Calculation and Optimization of Solid Launch Vehicle Trajectory[J].Journal of Solid Rocket Technology,1997,20(1):1-5.)

[8] Huang P X, Wei C Z, Gu Y B,et al. A Symplectic Optimization Method for Rapid Endo-Atmospheric Ascent Trajectory Planning[J]. International Journal of Modelling, Identification and Control, 2015,24(3): 196-205.

[9] Lu P, Pan B F. Highly Constrained Optimal Launch Ascent Guidance[J]. Journal of Guidance, Control, and Dynamics, 2010,33(2): 404-414.

[10] Gath P F, Calise A J. Optimization of Launch Vehicle Ascent Trajectories With Path Constraints and Coast Arcs[J]. Journal of Guidance, Control, and Dynamics, 2001,24(2):296-304.

[11] Brown K R, Harrold E F, Johnson G W. Some New Results on Space Shuttle Atmospheric Ascent Optimization[C]. AIAA Guidance, Control and Flight Mechanics Conference, Santa Barbara, California, America, 1970:3-8.

[12] 傅瑜,陈功,卢宝刚,等. 基于最优解析解的运载火箭大气层外自适应迭代制导方法[J]. 航空学报,2011,32(9):1696-1704.(Fu Yu, Chen Gong, Lu Baogang. A Vacuum Adaptive Iterative Guidance Method of Launch Vehicle Based on Optimal Analytical Solution[J]. Acta Aeronautica & Astronautica Sinica, 2011,32(9):1696-1704.)

[13] Jezewski D J. An Optimal, Analytic Solution to the Linear Gravity, Constant Thrust Trajectory Problem[J]. Journal of Spacecraft and Rockets, 1971,8(7):793-796.

[14] Mac Pherson, Duncan. An Explicit Solution to the Powered Flight Dynamics of a Rocket Vehicle[R]. TDR-169(3126) TN-2,1962.

[15] Jing W X, Zheng X, Wei P X, et al. An Ascent Iterative Guidance Algorithm for Solid Rocket Concerned with Multi-Constraints [C]. 27th Chinese Control and Decision Conference ( CCDC),2015,Qingdao,China.

[16] Calise A J Tandon S, Young D H, et al. Further Improvements to a Hybrid Method for Launch Vehicle Ascent Trajectory Optimization[C].AIAA Guidance, Navigation, and Control Conference and Exhibit,Denver,CO,America,2000:1-10.