数控电加工机床伺服跟踪软件算法及应用研究
2018-05-18顾洪良倪敏敏陆晓华
吴 强,顾洪良,倪敏敏,陆晓华
(苏州电加工机床研究所有限公司,江苏苏州215011)
对于数控电火花加工设备(如:电火花成形机床、高速电火花小孔加工机床和电火花线切割机床等),必须通过监测放电间隙状况来控制数控伺服轴的插补运动,这类控制伺服轴运动的方法被称为“伺服跟踪”。这种伺服跟踪控制方法的优劣,直接影响电火花加工设备的加工性能。在加工过程中,伺服跟踪通过控制加工轴的运动,保证了放电加工持续、稳定、高效地进行。
1 电加工机床数控系统伺服跟踪实现方法
1.1 传统硬件伺服跟踪电路结构
以往的电加工机床一般采用传统的硬件伺服系统实现伺服跟踪,其电路主要由间隙采样、电压比较、压频变换等单元组成,如图1所示。系统采样间隙伺服电压通过运放得到间隙电压与给定电压的差值,即 △U=Kv·(Ve-Vg),其中 Ve 为间隙平均电压;Vg为伺服给定电压;Kv为运放放大倍数。电压差值一路送入电压比较器,得到伺服方向信号Dir,其受控于 △U 的电平正负,即:Ve>Vg时,伺服跟踪方向为正向;Ve≤Vg时,伺服跟踪方向为反向。另一路△U送入线性压控振荡器,得到伺服脉冲信号 CP,脉冲频率 Fs=Kf·△U=Kv·Kf(Ve-Vg)。

图1 伺服跟踪方法结构框图
由此可求得伺服跟踪参数:伺服跟踪方向为Dir=Ve-Vg,这里Dir只取符号;伺服跟踪速度(即为脉冲频率)为 Fs=K·(Ve-Vg),这里 K=Kv·Kf,其实质是伺服跟踪系统的放大倍数,可通过调节Kv达到调节跟踪灵敏度的目的。
由以上分析得知,传统伺服跟踪系统是通过检测放电间隙的平均电压,设定伺服跟踪控制参数(给定电压和灵敏度),并经过电路计算,求得伺服跟踪信号,即跟踪方向和跟踪速度。
1.2 伺服跟踪原理分析
通过传统伺服跟踪系统的分析可知,机床数控轴对于放电间隙状况的跟踪,其实质是对放电间隙电压的跟踪。因此,系统可简化为对一电压值进行反馈调节的自动控制,其过程是通过不断调节伺服轴的运动参数,即方向和速度,控制间隙电压值一直保持等于给定电压值。但在实际情况下,间隙放电状况错综复杂、瞬息万变,且控制的伺服轴是个较大的惯性系统,控制滞后较大。因此,能将间隙电压尽可能地控制于给定电压附近,达到动态平衡状态,是较佳的控制目的。实际加工实验表明,当间隙电压控制于给定电压附近时,系统的灵敏度应较小,甚至趋近于零,使伺服轴保持在当前运动状态;当间隙电压远离于给定电压时,系统灵敏度要加大至合适的值,使其伺服轴尽快地跟上电压变化的节奏。这种传统伺服跟踪方法,其实质是一个线性系统,功能简单可靠,在要求不高的情况下也能胜任加工要求。但对于伺服跟踪要求较高,特别是针对电火花微小孔加工、单向走丝电火花线切割加工及多轴联动的电火花加工而言,显然力不从心,其缺陷主要有以下几方面:
(1)稳定性差。系统采用全部硬件的方法,所有的检测参数和设定跟踪参数均为模拟量,易受电路的干扰而变得失真且不可靠。
(2)性能有限。系统为线性系统,所有工作点的灵敏度都一样,伺服跟踪性能会大打折扣。
(3)适应性差。不能适应不同的应用,电路调整繁琐。
因此,理想的系统是能自动调节的非线性系统,而不是传统的线性系统。为了实现非线性控制,本文提出了采用下位机微处理器的伺服跟踪方法。
2 微处理器的伺服跟踪实现方法
本文提出了一种针对不同类型的数控电加工机床及采用下位机微处理器完成此类伺服跟踪的方法和软件算法。根据放电间隙状态的反馈参数,微处理器通过伺服跟踪算法向上位数控系统传递伺服跟踪参数,再由伺服系统完成插补指令。
电加工设备的数控系统有别于传统的数控机床。在加工过程中,伺服轴的每一步动作指令与当前放电间隙的状况息息相关。这就要求数控系统具备卓越的实时性能,以便快速响应下位微处理器传递的伺服跟踪参数。如此,由下位微处理器组成的控制系统持续地检测放电间隙状况,通过软件算法,计算出伺服跟踪参数,传递给上位数控系统,再由数控系统根据跟踪参数和插补指令控制伺服轴的运动,保证放电加工持续、稳定、高效地进行,这就是系统的控制过程。
(1)间隙电压的检测
间隙电压检测是由SPI接口的高速AD采样,微处理器通过SPI中断不间断地完成数据采集。经多次采集,并计算出电压的平均数,可得到间隙平均电压Ve。
(2)伺服跟踪控制参数
伺服跟踪控制参数包含伺服给定电压Vg和伺服灵敏度K,由主机设定并通过串口传递给微处理器。图2是系统的结构框图,上位机为数控系统主机,下位机为一微处理器。主机通过RS485串口向微处理器传送加工过程中设定的伺服跟踪给定电压Vg和伺服灵敏度K等参数,由专用的快速IO端口向主机传递伺服方向Dir和脉冲CP等跟踪参数。由于实时性要求,主机配有快速定时中断,以便快速响应跟踪参数。数控系统每接收到一个运动脉冲,并根据方向信号,决定插补指令向前或向后移动一个步当量。这里,运动脉冲的频率Fs即为伺服运动轴的运动速度。反映间隙状况的信号为间隙平均电压,由串口AD采样检测,发送至微处理器。

图2 系统架构框图
3 微处理器的伺服跟踪算法
3.1 微处理器伺服跟踪系统的数学模型
由以上分析可知,理想伺服跟踪的系统应该是一种合适的非线性系统。本文采用较简单且易于实现软件算法的二次函数作为系统数学模型。系统相关参数的函数表达式如下:
伺服方向:Dir=Ve-Vg+△V
伺服脉冲:Fs=K·(Ve-Vg)2+△F
其中:Ve为间隙电压;Vg为给定电压;K为系统预设的灵敏度;△V为电压偏移量;△F为频率偏移量;Dir表达式只取符号值;Fs为脉冲频率,即为伺服速度。
图3是二次函数曲线,通过观察可发现:
(1)最佳伺服跟踪点为曲线的极值点,即Ve=Vg时。伺服跟踪的稳定区域在极值点附近,该区域曲线较平滑,斜率较缓,即系统倍率最小,系统最“迟钝”。加工在此区域内,跟踪易被“咬住”,且一旦落入此区域内,也不会轻易“跑出去”。
(2)越是远离极值点,即△U绝对值越大,曲线斜率越陡,系统倍率越大,系统越灵敏。系统就能较快地找到稳定状态。
(3)为设定不同K值,而相同Vg值的两条曲线,即为灵敏度不同而给定电压相同,两曲线的极值点为同一点。当给定不同的Vg时,只需将原曲线在X轴方向作平移即可。这说明,伺服给定电压Vg和灵敏度K作为跟踪控制参数,均是单独控制,不会相互串扰而影响结果。
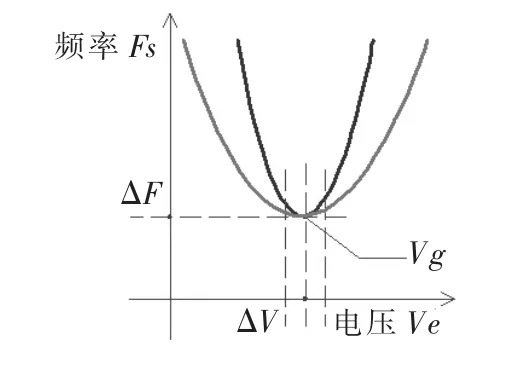
图3 非线性伺服控制算法曲线
3.2 针对不同电加工机床的伺服跟踪算法应用
前文只是给出了一般控制的伺服跟踪数学模型,针对不同的应用场合,必须为适应加工而采取不同的算法。针对电火花成形、电火花小孔、电火花线切割等3种应用最广泛的电加工机床,其二次函数曲线分别见图4a~图4c。

图4 典型电加工机床伺服控制算法的二次函数曲线
3.2.1 电火花成形加工
根据电火花成形加工特点,给出其伺服跟踪函数的数学表达式:
当 Ve>Vg 时,Fs=K·(Ve-Vg)2;
当 Ve 该表达式包含了伺服跟踪的方向和脉冲速度两个跟踪参数,表达式的值为伺服速度,表达式的正负号为伺服方向。 3.2.2 高速电火花小孔加工 高速电火花小孔加工与成形加工相类似,区别是多了一个参数Fg,其数学表达式如下: 当 Ve>Vg 时,Fs=K·(Ve-Vg)2+Fg; 当 Ve 与成形加工一样,表达式的值为伺服速度,表达式的正负号为伺服方向。这里的参数Fg所代表的实际意义是:高速小孔加工不同于成形加工,在加工过程中,其蚀除工件的速度较快,当伺服跟踪处于最佳状态时,即Ve=Vg,伺服轴的跟踪速度即为Fg。当Ve 电火花成形加工的表达式本质是一样的,只是其蚀除工件速度较慢,Fg趋近于零。 3.2.3 电火花线切割加工 电火花线切割加工与小孔加工相类似,区别是其伺服方向只有正向,其数学表达式如下: 当 Ve>Vg 时,Fs=K·(Ve-Vg)2+Fg; 当 Ve 线切割加工与小孔加工的共同点是都需要参数Fg,表达式是一样的。区别在于当Ve 3.2.4 初始进给速度Fg的整定 上述小孔加工和线切割伺服控制中都增加了一个控制参数Fg,其实质是最佳跟踪速度。Fg的整定可由微处理器根据加工状况通过一定算法自动设定。其过程如下:在开始加工初期,设置一段时间的试加工状态,先将系统灵敏度K设为零,再由零开始逐步增加Fg的值,直至间隙电压接近于给定电压,此时的Fg值就整定结束。然后,在正式加工过程中,根据稳定情况小幅修正Fg的值。这样,系统也有了智能化的自学习功能了。 经试验验证,本文提出的伺服跟踪方法在电火花成形、线切割加工中,间隙电压稳定度和脉冲电源放电效率均获得了较满意的提升,对间隙空载率、短路率及放电异常率也有较明显的抑制,且在精细放电加工应用时,由于稳定的跟踪性能,间接提升了脉冲电源的性能。该方法基本具备了微处理器自动计算最优控制参数的智能化功能,但仍需设定伺服电压及灵敏度两个参数,若能将此参数通过系统算法自动进行整定,就能初步实现无人工干预的完全智能化,这也是将来需进一步研究的方向。4 结束语
