基于SAS与R软件的主成分分析
2018-05-18胡良平
胡良平
(1.军事科学院研究生院,北京 100850;2.世界中医药学会联合会临床科研统计学专业委员会,北京 100029 *通信作者:胡良平,E-mail:lphu812@sina.com)
1 概 述
1.1 基本概念
在科学研究中,经常需要从同一个体(或观测单位)上观测多个指标,这些指标从不同方面反映个体的性质。但指标太多,不仅会增加计算的复杂性,也会给合理分析问题和解释问题带来困难。表面上,各指标之间地位相同。实际上,各指标所包含的信息量参差不齐,且指标间往往不是相互独立的,它们所包含的信息有交叉或重叠的部分。所以,需要对众多指标进行适当的处理,以便更好地反映事物的本质特征。
1.2 何为主成分分析
主成分分析(principal components analysis)是将多个定量指标转换为少数几个综合指标的一种统计分析方法。它是将彼此相关的一组变量转化为彼此独立的一组新变量,并以其中少数的几个新变量综合反映原先多个变量所包含的主要信息,且这少数几个综合变量具有独特的专业含义。主成分变量实际上就是由原变量X1~Xm线性组合出来的m个互不相关、且未丢失任何信息的新变量,也称为综合变量。
1.3 主成分分析的作用
多指标的主成分变量常被用来揭示某种事物或现象内在规律性的综合指标,研究者结合基本常识和专业知识对综合指标所蕴藏的信息予以恰当解释,就可以更深刻地揭示事物的内在规律。主要应用于以下三个方面:①降维,即利用较少的几个主成分变量就可以取代原来众多的变量所承载的信息;②基于消除多重线性回归分析中自变量间共线性关系之后的主成分变量再进行回归分析,即所谓的“主成分回归分析”;③应用于综合评价领域,就是基于综合评价指标在各个体上的“取值或得分”对全部个体或观测单位进行排序,还可进一步对其进行分档。这种做法和结果事实上就是将原先的“无序样品”转变成“有序样品”,此时,就相当于对“有序样品”进行聚类分析了。
1.4 适合进行主成分分析的数据结构[1]
1.4.1 问题与数据结构
【例1】某文献计量学家收集到23种肿瘤类期刊的载文量(X1)、基金论文比(X2)、总被引频次(X3)、影响因子(X4)、5年影响因子(X5)、即年指标(X6)、被引半衰期(X7)和Web即年下载率(X8)8个指标的具体数据。见表1。
1.4.2 对数据结构的分析
在表1中,23种期刊都是肿瘤学方面的期刊,故可认为它们具有“同质性(简单地理解,就是具有可比性)”;X1~X8这8个计量指标都是用来反映每种学术期刊的影响力、知名度、学术和社会价值等,而且,这些指标的取值都是越大越好,即所谓的“高优指标”。显然,从“性质”上来看,这些指标也是具有“同质性(简单地理解,就是具有可比性)”的。满足以上两方面(横向被称为“样品”、纵向被称为“变量”)要求的资料,称为“单组设计多元定量资料”。
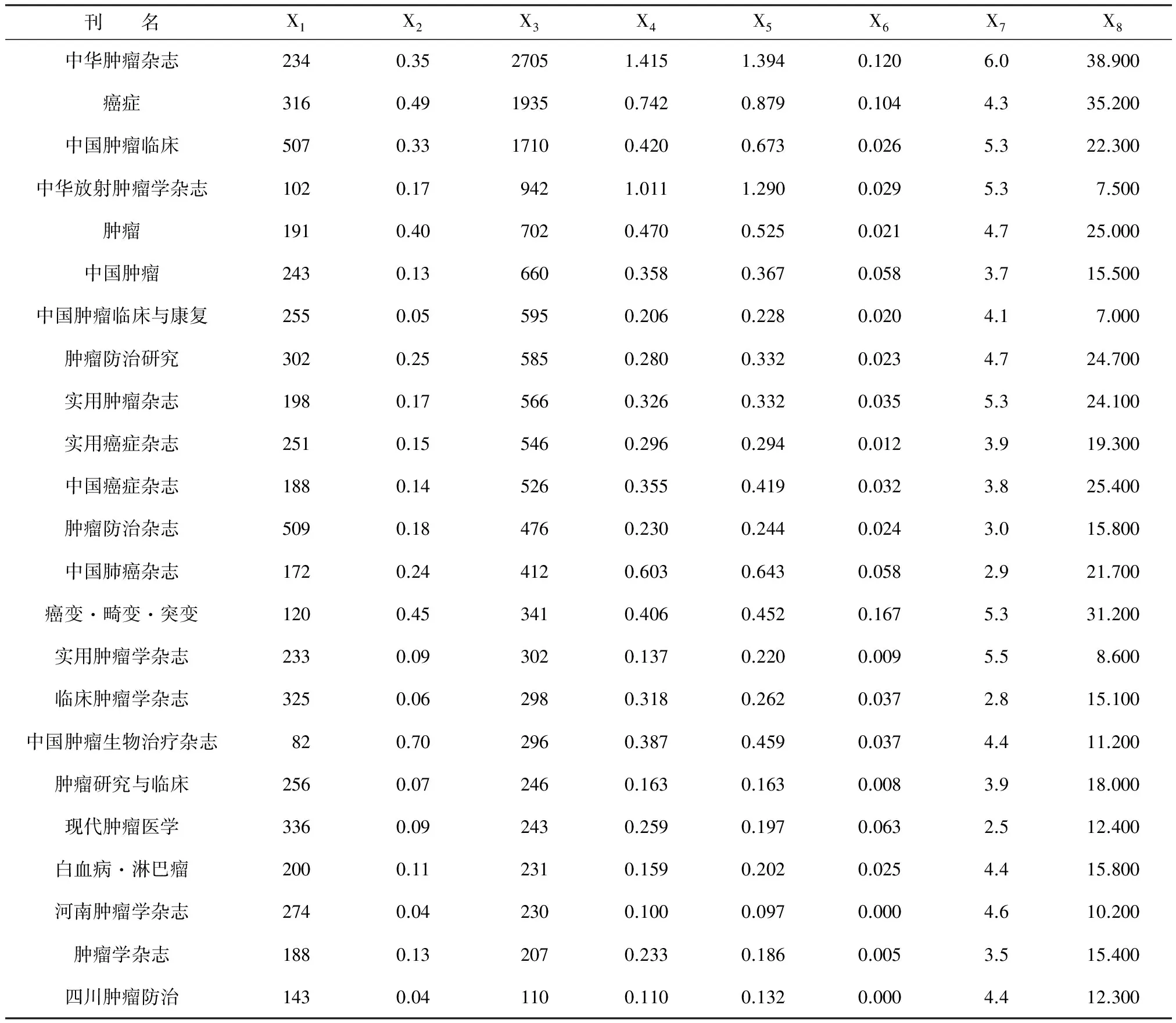
表1 23种肿瘤类期刊的文献计量学指标及其取值
1.4.3 适合选用的统计分析方法
对于前面所呈现的“单组设计多元定量资料”而言,可以选用哪些多元统计分析方法呢?使人惊讶的是:适合分析这种数据结构的多元统计分析方法占据了全部多元统计分析方法的绝大部分。具体来说,需要按以下两种情形来划分:
(1)不提供任何附加信息
可以选择的多元统计分析方法有以下5种:①无序样品聚类分析法;②变量聚类分析法;③主成分分析法;④探索性因子分析法;⑤对应分析法。
(2)提供某些附加信息
可以选择的多元统计分析方法有以下7种:①单组设计多元方差分析(需要提供各指标的标准值);②通径分析(需要提供通径图,即依据基本常识和专业知识绘制出变量之间相互依赖关系的图形);③证实性因子分析[需要提供通径图,即依据基本常识和专业知识绘制出变量之间相互依赖关系的图形,变量包括“显变量(可观测其取值的变量)”与“隐变量(不可观测其取值的变量)”];④结构方程模型分析[需要提供通径图,即依据基本常识和专业知识绘制出变量之间相互依赖关系的图形,变量包括“显变量(可观测其取值的变量)”与“隐变量(不可观测其取值的变量)”];⑤多维尺度分析(需要提供任何两个样品之间相似度或不相似度系数,全部系数构成相似度或不相似度矩阵);⑥典型相关分析(需要依据基本常识和专业知识将全部变量划分为两类);⑦复相关分析(需要指出一个变量为因变量、其他变量为自变量)。
2 主成分分析的实现
2.1 基于SAS实现计算
2.1.1 所需要的SAS程序
将表1中的23行9列数据按文本格式存储在“F:CCC”文件夹中,命名为“23种肿瘤类期刊文献计量学指标资料.txt”;设所需要的SAS程序名为“基于肿瘤类期刊文献计量学指标进行主成分分析.SAS”:
data a1;
infile 'F:CCC23种肿瘤类期刊文献计量学指标资料.txt';
input name $20. x1-x8;
run;
proc princomp data=a1 out=b1 prefix=z;
var x1-x8;
run;
2.1.2 SAS程序主要输出结果及解释
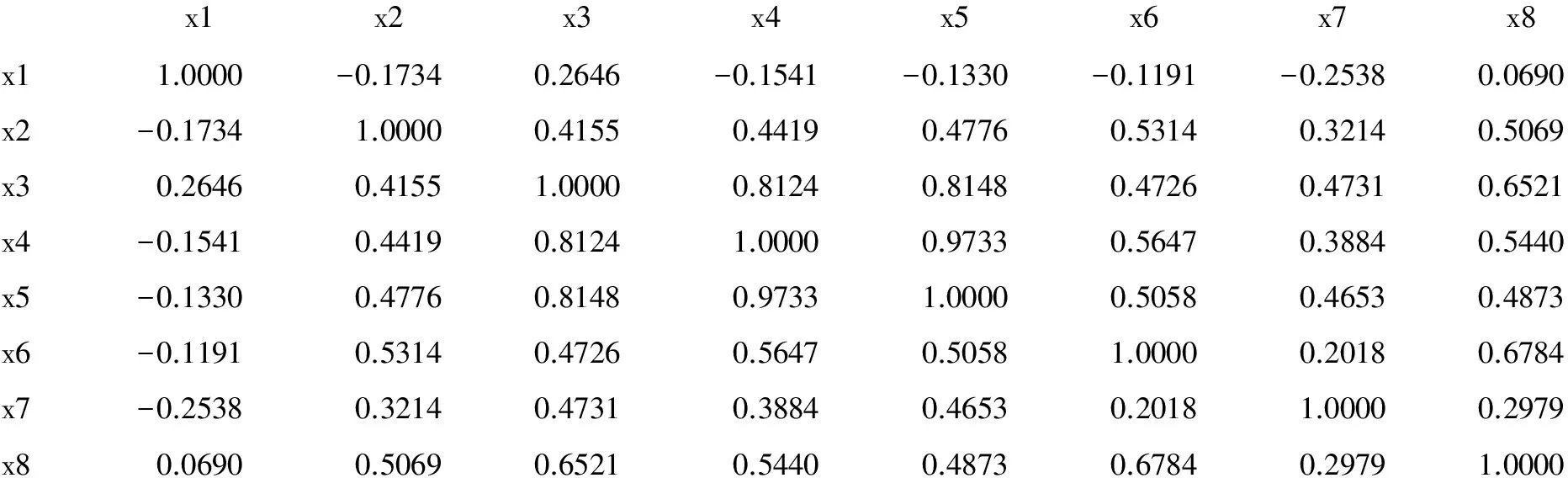
相关矩阵
以上为8个计量变量两两之间的Pearson相关矩阵。
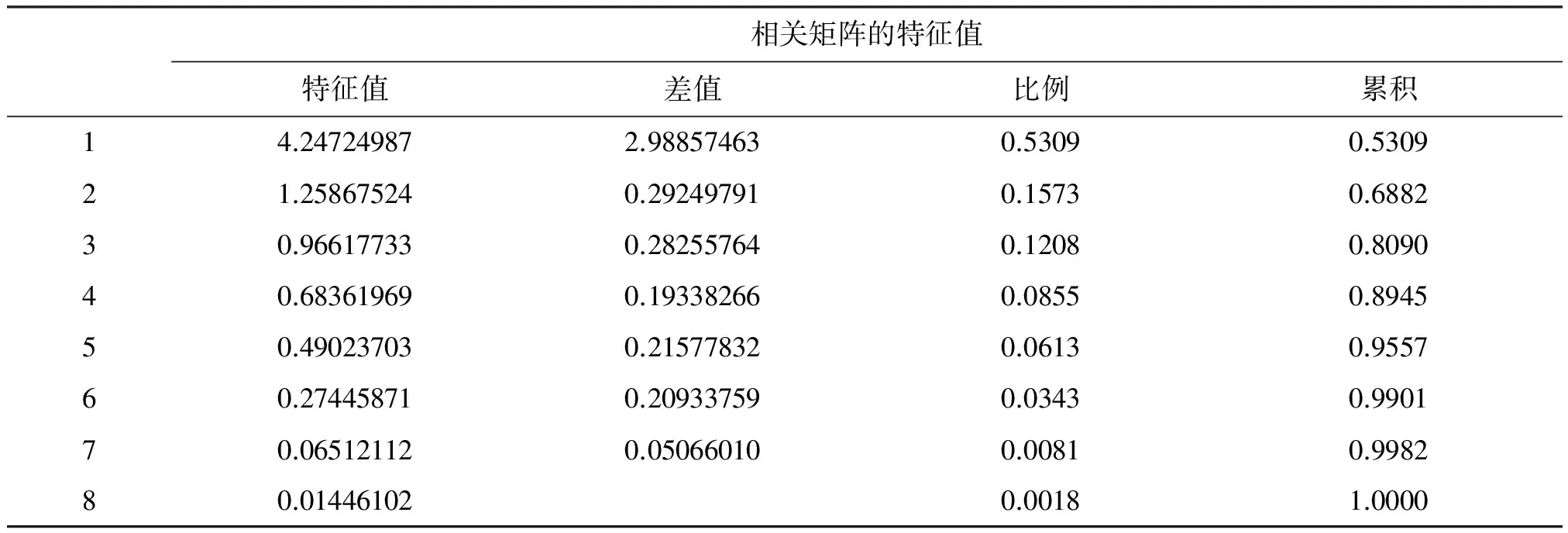
相关矩阵的特征值特征值差值比例累积14.247249872.988574630.53090.530921.258675240.292497910.15730.688230.966177330.282557640.12080.809040.683619690.193382660.08550.894550.490237030.215778320.06130.955760.274458710.209337590.03430.990170.065121120.050660100.00810.998280.014461020.00181.0000
以上为相关矩阵的特征值、相邻两特征值之差量、各特征值占总特征值(=8)的比例和累计百分比。
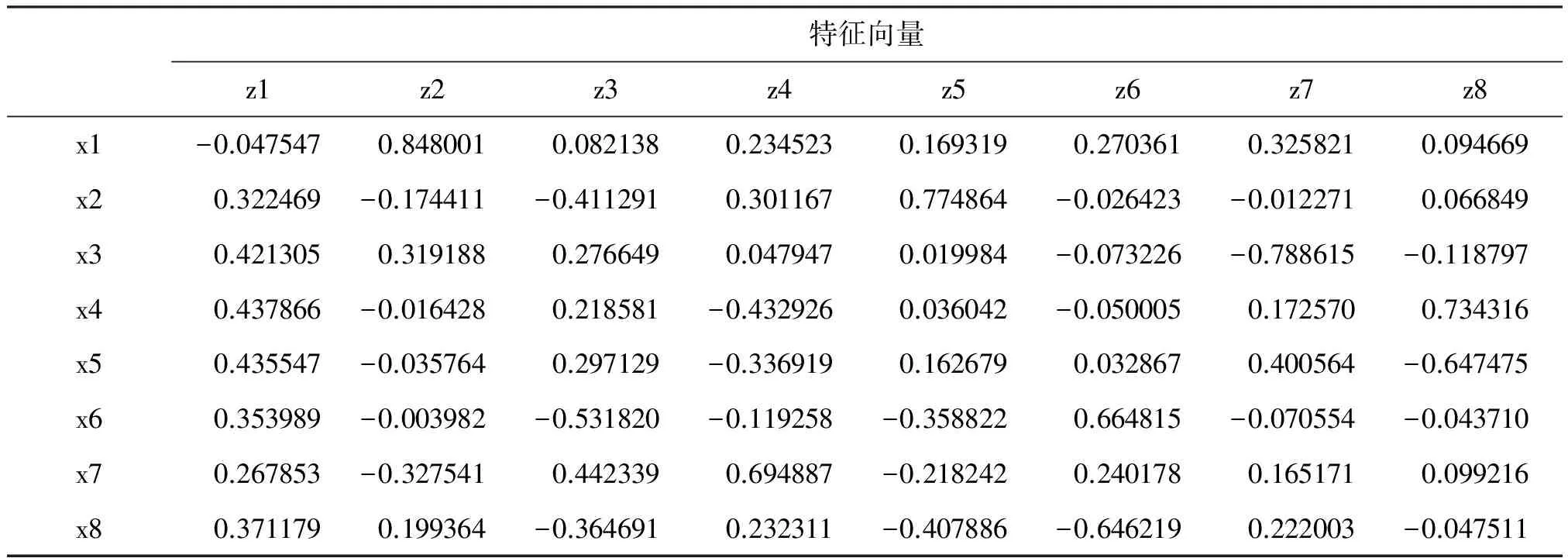
特征向量z1z2z3z4z5z6z7z8x1-0.0475470.8480010.0821380.2345230.1693190.2703610.3258210.094669x20.322469-0.174411-0.4112910.3011670.774864-0.026423-0.0122710.066849x30.4213050.3191880.2766490.0479470.019984-0.073226-0.788615-0.118797x40.437866-0.0164280.218581-0.4329260.036042-0.0500050.1725700.734316x50.435547-0.0357640.297129-0.3369190.1626790.0328670.400564-0.647475x60.353989-0.003982-0.531820-0.119258-0.3588220.664815-0.070554-0.043710x70.267853-0.3275410.4423390.694887-0.2182420.2401780.1651710.099216x80.3711790.199364-0.3646910.232311-0.407886-0.6462190.222003-0.047511
以上为8个特征值对应的特征向量。选取几个主要的主成分变量就可近似取代原先8个变量信息的直观判断方法见图1。
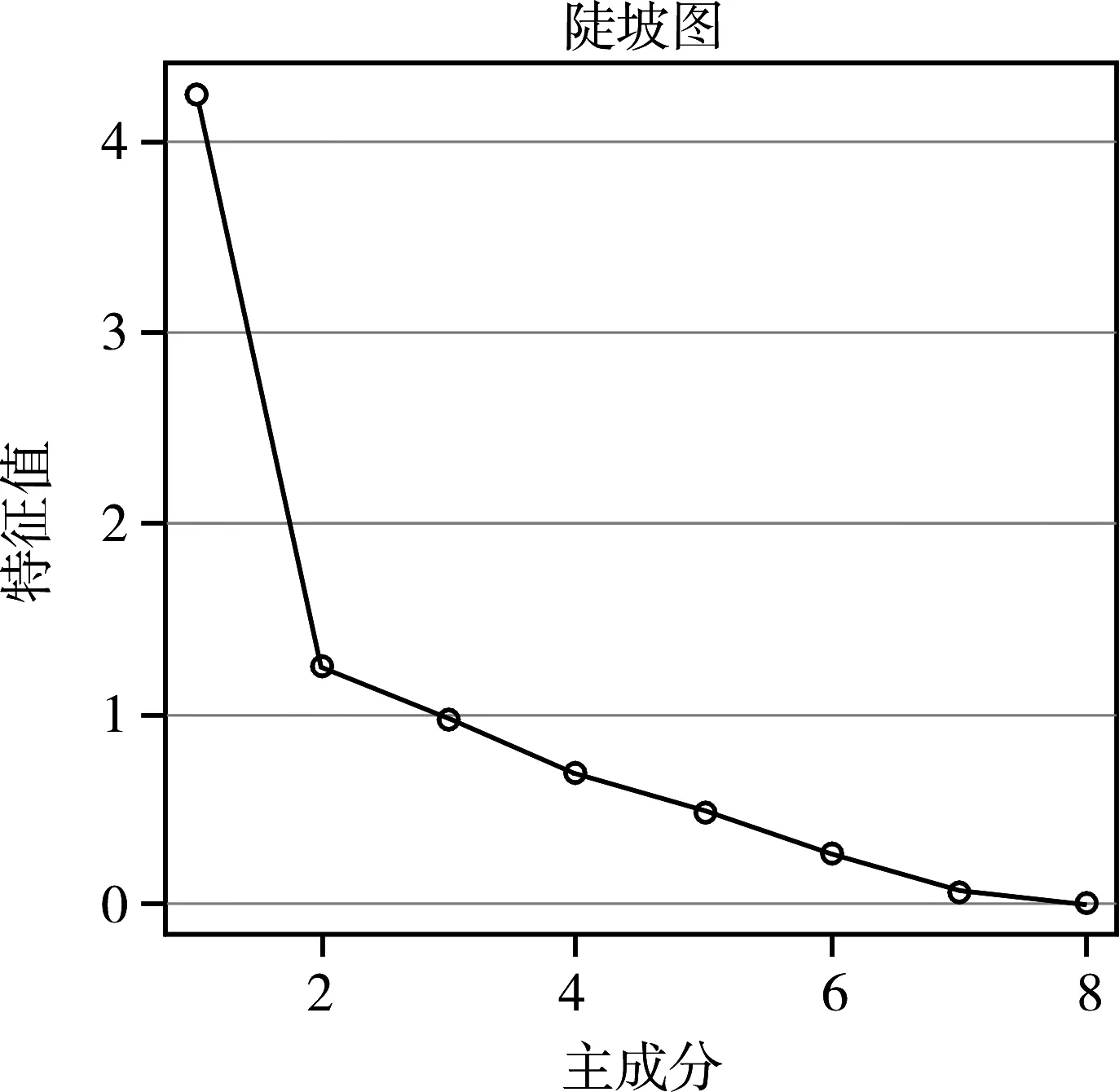
图1 碎石图
由图1可知:在主成分变量为2个时,折线出现了明显的“拐点”,也就是说,取前两个主成分变量,就可近似反映原来的8个原变量所包含的信息。
各主成分变量携带的信息量占总量8的比例见图2。
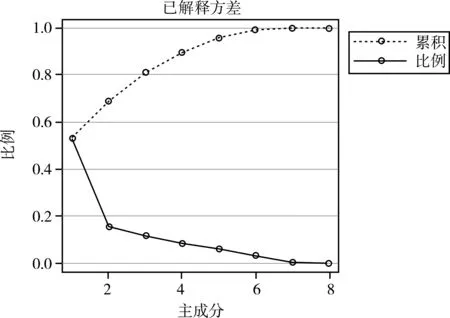
图2 各主成分变量携带的信息量占总量8的比例
由图2可知:下面的折线代表各主成分变量携带的信息量占总量8的比例,上面的折线代表各主成分变量对应的特征值累积后的结果。
下面写出第一个主成分变量的线性表达式(系数来自“特征向量”第1列):
z1=-0.047547x1+0.322469x2+0.421305x3+0.437866x4+0.435547x5+0.353989x6+0.267853x7+0.371179x8
利用“特征向量”中的系数,可以写出第2~8个主成分变量的表达式。
值得注意的是:“特征向量”中的各列系数都是采取了标准化变换(即每个变量减去其算术平均值除以标准差)而获得的,若希望用原变量表达出来,需要进行相反的变换,此处从略。
2.1.3 如何给主成分变量命名
(1)选取几个主成分变量
应结合特征向量各列的系数,给前几个主要的主成分变量命名。究竟应该关注前几个主成分变量呢?一般采取两种决定方法之一:第一种,选取特征值≥1的那几个主成分变量;第二种,选取累计贡献率达到85%左右时所对应的那几个最大和较大特征值所对应的主成分变量。在本例中,若按前者来选取,就选两个主成分变量;若按后者来选取,就需要选4个主成分变量了。
(2)给选取的前两个主成分变量命名
命名的依据:根据各列特征向量的系数的绝对值大小及其左侧变量的专业含义来给各列主成分变量命名。第一主成分变量可以命名为:除“载文量”之外的其他7个文献计量指标的综合效应指标;而第二主成分变量可以命名为:“载文量”与“总被引频次”2个文献计量指标的综合效应指标。
2.2 基于R软件实现计算[2]
2.2.1 所需要的R程序
将表1中的23行9列数据按文本格式存储在“F:CCC”文件夹中,命名为“23种肿瘤类期刊文献计量学指标资料含变量名.txt”;设所需要的R程序名为“基于肿瘤类期刊文献计量学指标进行主成分分析.txt”:
#设置路径为"F://CCC/"
setwd("F://CCC/")
#下面data1中的数据为23行9列
data1<- read.table("23种肿瘤类期刊文献计量学指标资料含变量名.txt",header=TRUE)
#删掉第1列:期刊名称
data<- data1[,-1]
attach(data)
#假定已安装stats子程序包
#install.packages("survival")
#加载stats子程序包
library(stats)
#基于princomp()函数且相关矩阵进行主成分分析
model1=princomp(data,cor=TRUE,scores=TRUE)
#系数保留4位小数
options(digits=4)
#输出模型1的分析结果
summary(model1,loading=TRUE)
#绘制模型1的碎石图
screeplot(model1,type="line",main="碎石图")
#基于模型1且前两个主成分变量绘制各指标的散布图
biplot(model1)
#计算各主成分变量在各样品上的预测值
predict(model1)
【R输出结果】
Importance of components:

Comp.1Comp.2Comp.3Comp.4Comp.5Comp.6Comp.7Comp.8Standarddeviation2.06091.12190.98290.826810.700170.523890.255190.120254ProportionofVariance0.53090.15730.12080.085450.061280.034310.008140.001808CumulativeProportion0.53090.68820.80900.894470.955740.990050.998191.000000
以上为第1部分输出结果,其中,第1行“标准差”实际上就是“特征值的平方根”。
Loadings:
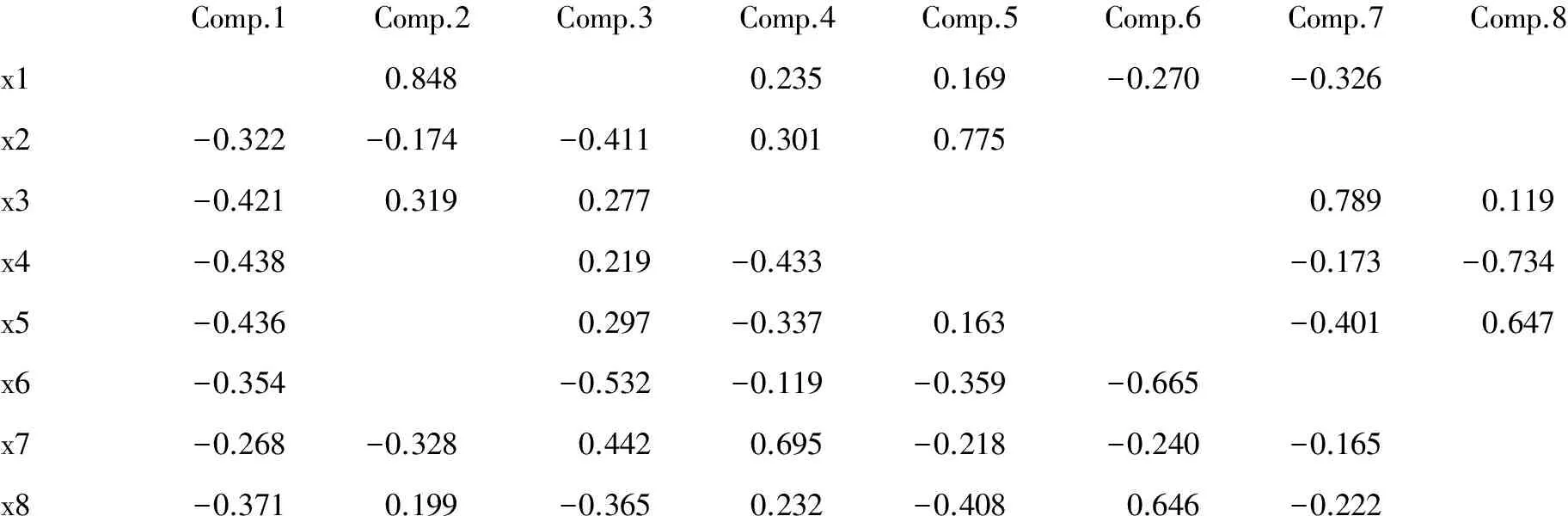
Comp.1Comp.2Comp.3Comp.4Comp.5Comp.6Comp.7Comp.8x10.8480.2350.169-0.270-0.326x2-0.322-0.174-0.4110.3010.775x3-0.4210.3190.2770.7890.119x4-0.4380.219-0.433-0.173-0.734x5-0.4360.297-0.3370.163-0.4010.647x6-0.354-0.532-0.119-0.359-0.665x7-0.268-0.3280.4420.695-0.218-0.240-0.165x8-0.3710.199-0.3650.232-0.4080.646-0.222
以上为第2部分输出结果,即“特征向量”,各列中空缺处为“0”。与前面“SAS输出的特征向量”进行比较,在第一主成分变量上“差距”非常大,很可能是“定义或算法(如:是否采取了坐标轴旋转)”不同所致。选取几个主要的主成分变量就可近似取代原先8个变量信息的直观判断方法见图3。
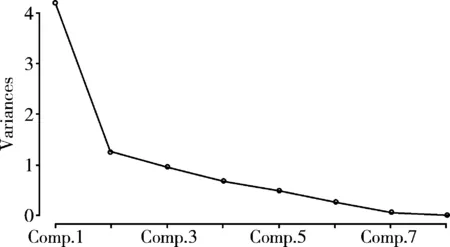
图3 碎石图
R软件还可以以第一主成分变量为横坐标轴、以第二主成分变量为纵坐标轴绘制出散布图(因篇幅所限,此图省略),从此图上可看出:在8个文献计量学指标中,唯独x1(载文量)很特别,其他7个指标的性质和表现比较接近。
因篇幅所限,各主成分变量在各样品上的预测值(或得分)从略。
【说明】在医学研究中,要谨慎使用主成分分析。关键在于:应注意本文中所提及的“数据结构”。若针对文献[3]的资料,如何使用主成分分析,请读者认真思考。
参考文献
[1] 胡良平. 面向问题的统计学——(3)试验设计与多元统计分析[M]. 北京: 人民卫生出版社, 2012: 19-39.
[2] 李诗羽, 张飞, 王正林. 数据分析: R语言实战[M]. 北京: 电子工业出版社, 2015: 211-220.
[3] 赵巍峰, 彭敏, 谢博, 等. 健康教育对精神分裂症患者病耻感影响的持续性[J]. 四川精神卫生, 2017, 30(6): 519-523.
