主成分分析应用(III)
——主成分判别分析
2018-05-18胡良平
胡良平
(1.军事科学院研究生院,北京 100850;2.世界中医药学会联合会临床科研统计学专业委员会,北京 100029 *通信作者:胡良平,E-mail:lphu812@sina.com)
1 概 述
1.1 基本概念
本期《基于SAS与R软件的主成分分析》一文介绍了“主成分分析方法”,此法不仅可以借用于多重线性回归分析(见本期《主成分分析应用(Ⅰ)——主成分回归分析》)和无序样品聚类分析(见本期《主成分分析应用(Ⅱ)——主成分聚类分析》)之中,还可以借用于判别分析或分类分析之中。
1.2 何为主成分判别分析
主成分判别分析(the principal components discrimination analysis)是对拟用于判别分析的定量变量先进行主成分分析,产生主成分变量,然后再基于这些主成分变量(注意:不是原变量)进行判别分析。
1.3 主成分判别分析的作用
将原先可能具有一定相关性的定量指标,通过主成分分析,使其转变成相互独立的变量,期望能够有利于缩小同一类样品之间的相对距离,同时,还有利于扩大不同类样品之间的相对距离,以便更好地对样品实现精准分类。
1.4 适合进行主成分判别分析的数据结构
1.4.1 问题与数据结构
【例1】有一个著名的数据集,即iris数据集,其中共有150个观测,4个定量的评价指标[Sepal.Length、Sepal.Width、Petal.Length、Petal.Width,分别代表萼片长度、萼片宽度、花瓣长度、花瓣宽度,单位都是毫米(mm)],1个代表分类的标签变量(species,种类)。共有3种花,即有setosa(刚毛的)、versicolor(杂色的)、virginica(尚未找到合适的中文翻译名),各有50个观测,数据结构见表1[1-2]。
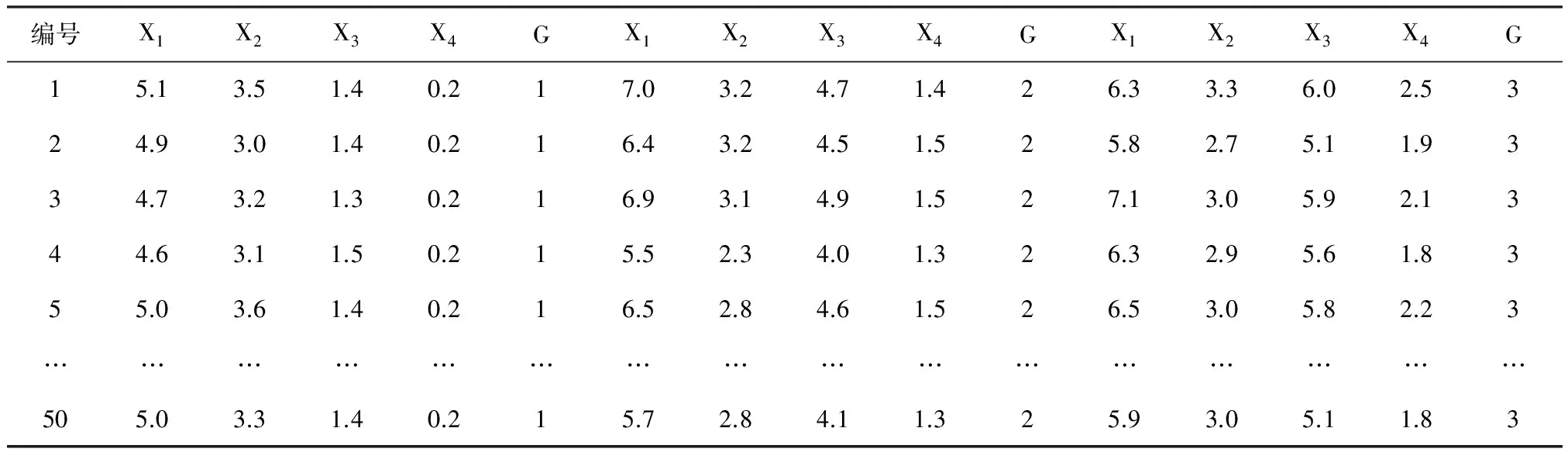
表1 三类鸢尾属植物4项定量指标的测定结果
1.4.2 对数据结构的分析
在表1中,有3类鸢尾属植物,其标签变量名为G,其具体代码分别为1、2、3,它可以被称为结果变量。显然,结果变量是多值名义变量,虽然其代码是三个数字,但仅代表三种种属的花。X1~X4这四个计量评价指标都是用来反映每种花的特征的,它们的取值并非越大越好,也不是越小越好。关键是期望它们能够很好地区分出不同种属的花。
1.5 样品判别分析的种类
1.5.1 概述
知道三种种属的花各有50株,期望基于这150株花在四项计量指标上的取值能构建一个计算公式,即判别函数式,用于对一株新的属于这三类之一的花的真实类别进行分类或判别。为了实现这一分析目的,可以基于多种不同的统计思想或思路来构造分析方法,通常有如下四类:①基于“距离”的判别分析法;②基于“贝叶斯先验概率”的判别分析法;③基于“投影”的判别分析法;④基于“机器学习”的判别分析法。
1.5.2 基于“距离”的判别分析方法[3-4]
就是基于定量评价指标计算出每一类中各样品之间的距离,再将各类样品的距离计算公式组合在一起,构成一个判别函数式,用于判定任何一个未知类别的样品的归属。
1.5.3 基于“贝叶斯后验概率”的判别分析方法[3]
就是基于“贝叶斯先验概率”来构造一个总的期望损失函数ECM,贝叶斯判别分析是取使ECM达到最小的划分。
1.5.4 基于“投影”的判别分析方法[3]
费希尔线性判别是把k个总体的所有p维空间的样本点投影到一维空间上,使得在一维空间中,来自不同总体的样本点能尽可能地被分开。
1.5.5 基于“机器学习”的判别分析方法[5-6]
“机器学习”是一种统计思想,基于其产生出许多高效的统计分析方法,主要实现两方面的统计功能,即“回归分析”和“判别分析”。根据解决问题时所采取的思路和关键技术不同,其具体的分析方法包括以下几种:①决策树分析法;②支持向量机分析法;③各种神经网络分析法;④随机森林分析法;⑤集成学习分析法等。
因篇幅所限,本文仅介绍基于“主成分变量”和“距离”的判别分析方法。
2 主成分判别分析的实现
2.1 所需要的SAS程序
将表1中的150行5列数据按文本格式存储在“F:CCC”文件夹中,命名为“150株鸢尾属植物四项评价指标资料.txt”;设所需要的SAS程序名为“基于150株鸢尾属植物四项评价指标资料进行主成分判别分析.SAS”:
proc format;
value specname
1='Setosa '
2='Versicolor'
3='Virginica ';
run;
data iris;
title 'Fisher (1936) Iris Data';
infile 'f:ccc150株鸢尾属植物四项评价指标资料.txt';
input SepalLength SepalWidth PetalLength PetalWidth Species;
format Species specname.;
label
SepalLength='Sepal Length in mm.'
SepalWidth ='Sepal Width in mm.'
PetalLength='Petal Length in mm.'
PetalWidth ='Petal Width in mm.';
symbol=put(Species,specname10.);
run;
proc princomp data=iris prefix=z out=bbb;
var SepalLength SepalWidth PetalLength PetalWidth;
run;
PROC DISCRIM data=bbb METHOD=NPAR K=6 MANOVA LISTERR CROSSLISTERR;
CLASS Species;
VAR z1-z4;
RUN;
2.2 SAS程序主要输出结果及解释
DISCRIM过程
以下校准数据的分类汇总:WORK.BBB
使用以下项的交叉验证汇总:6个最接近的邻近值
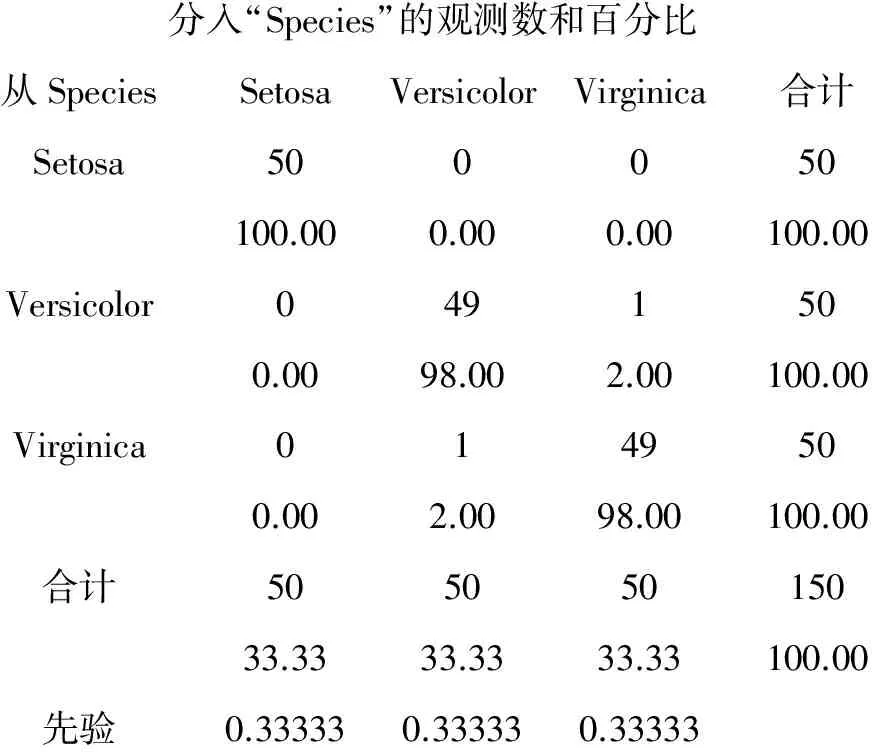
分入“Species”的观测数和百分比从SpeciesSetosaVersicolorVirginica合计Setosa500050100.000.000.00100.00Versicolor0491500.0098.002.00100.00Virginica0149500.002.0098.00100.00合计50505015033.3333.3333.33100.00先验0.333330.333330.33333
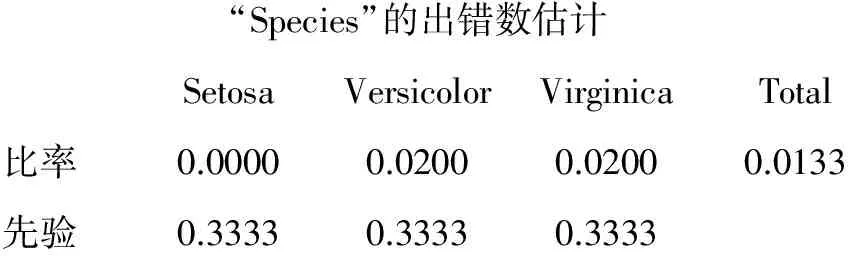
“Species”的出错数估计SetosaVersicolorVirginicaTotal比率0.00000.02000.02000.0133先验0.33330.33330.3333
以上结果表明:第2类和第3类各有一个样品被分错了。
值得一提的是:本例资料经过主成分变换后的判别分析结果与未经过主成分变换的判别分析结果[1-2]一致。换句话说,是否有必要采取主成分判别分析有待进一步研究。
参考文献
[1] 胡良平. 医学统计学——运用三型理论进行多元统计分析[M]. 北京: 人民军医出版社, 2010: 188-240.
[2] 胡良平. SAS常用统计分析教程[M]. 2版. 北京: 电子工业出版社, 2015: 575-588.
[3] 茆诗松. 统计手册[M]. 北京: 科学出版社, 2006: 539-546.
[4] 薛薇. R语言数据挖掘方法及应用[M]. 北京: 电子工业出版社, 2016: 122-141.
[5] 周志华. 机器学习[M]. 北京: 清华大学出版社, 2016: 73-196.
[6] 吴喜之. 复杂数据统计方法——基于R的应用[M]. 3版. 北京: 中国人民大学出版社, 2015: 41-56.
