基于伸臂桁架多尺度模型的超高层建筑地震灾变评估

卢 啸，吕泉林，徐龙河，李 易

(1. 北京交通大学土木建筑工程学院，北京 100044；2. 北京工业大学建筑工程学院，北京 100124)

随着高层建筑的迅速发展，建筑的高度不断增加，如果仍然采用传统的框架-核心筒等结构体系，就不可避免地要遇到结构在水平荷载作用下水平位移过大、剪力墙或筒体弯矩过大等问题.因此，巨柱-伸臂-核心筒结构体系成为了现代超高层建筑的主要抗侧力体系之一.伸臂桁架作为连接外围巨柱和内部核心筒的主要构件，当结构承受水平荷载时，核心筒通过伸臂桁架，将弯矩转化为轴力传递到外围巨柱中，使巨柱起着类似拉压杆的作用，从而使得外围巨柱与内部核心筒共同受力达到提高抗侧力能力的目的.可见，伸臂桁架对整个超高层建筑的抗震性能有着重要的作用.

然而，在目前超高层建筑整体结构抗震性能研究中，由于受到试验能力和费用等条件的限制，数值模拟方法成为了主要的研究手段之一.由于钢结构规范通过宽厚比等构造措施限制了构件的弹性屈曲，因此，在设计阶段或建立有限元模型时，伸臂桁架大都采用基于梁单元的宏观模型来进行模拟[1-4].虽然宏观模型可以提高计算效率，但仍然存在一些问题.比如钢构件在屈服后会出现局部屈曲的现象[5-6]，在伸臂桁架的构件试验中，也经常能观察到该现象[7-8]，这种弹塑性屈曲会降低构件的屈服后承载力和刚度，采用宏观的梁单元则很难对这一过程进行模拟.因此，在研究构件层次的力学特性时，大部分学者采用精细有限元模型(壳单元或实体单元)来对构件的力学行为进行模拟[9-11].精细有限元模型虽然预测结构较准确，但单元数量较多，计算量大.而超高层建筑体系复杂，构件种类和数量繁多，如果均采用壳和实体单元模拟，现有的计算能力很难满足计算需求.

因此，随着数值模拟技术的不断进步，为了解决计算效率和精度的问题，多尺度分析技术应运而生.结构的多尺度分析是指对同一结构模型中的不同部分，根据不同的分析需求，建立不同类型或尺度的有限元模型，并在不同尺度之间建立合理的连接方式，使整体结构变形协调.众多学者已经对多尺度分析技术在建筑结构中的运用进行了大量探索.如 Li等[12]建立了青马大桥的多尺度模型，对其动力响应和局部损伤进行了研究；陆新征等[13]提出了宏观模型和细观模型的界面连接方法，并运用于某6层框架的抗震性能分析；潘建荣等[14]建立了钢管混凝土柱-钢梁节点的多尺度模型，研究了半刚性组合平面框架体系的抗震性能.由于超高层建筑的重要性程度高，且伸臂桁架对结构的抗震性能有较大的影响，忽略伸臂桁架的弹塑性屈曲可能会影响超高层结构地震灾变预测结果的准确性.因此，本文以典型的伸臂桁架试验为基础，研究精细化模型与宏观模型计算精度的差异，并提出兼顾计算精度和效率的伸臂桁架多尺度模型；选取典型超高层巨型组合结构，建立超高层巨型组合结构的多尺度计算模型，重点研究伸臂桁架塑性屈曲对超高层巨型组合结构地震灾变过程、倒塌模式和抗倒塌能力的影响.

1 伸臂桁架多尺度模型

1.1 宏观与精细模型差异

伸臂桁架作为超高层建筑中的重要抗侧力构件，已有学者对其抗震性能进行了构件试验研究.如赵宪忠、陈以一等[7-8]对上海中心大厦的典型伸臂桁架的抗震性能进行了研究.试验选取了靠近核心筒端的伸臂桁架的一个节间，分别进行了单调加载和循环加载试验，构件主要尺寸及加载示意如图 1所示，其中 F为竖向千斤顶力加载过程中力的大小.文献中为了保持上弦杆、腹杆和下弦杆的轴力比例为 1∶10∶1，3个作动器按照 1.15∶1.00∶0.04的比例加载，加载到罕遇地震水平时再按照竖向千斤顶的位移控制，但仍然保持3个千斤顶的力的比例不变.

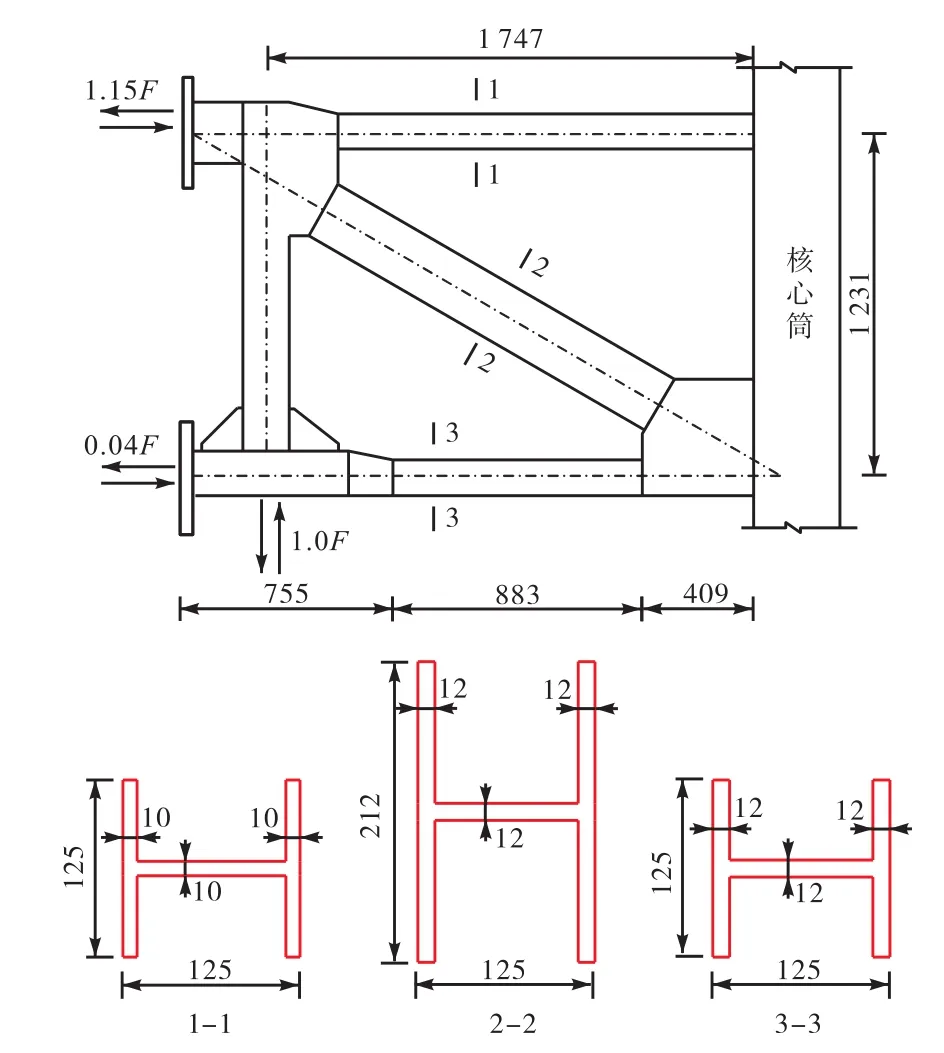
图1 构件主要几何尺寸及加载示意(单位：mm)Fig.1 Main dimensions of specimen and loading diagram(unit：mm)

根据图 1的构件尺寸，采用 MSC.Marc有限元软件中的78号薄壁梁单元按照构件的轴线建立了伸臂试件的宏观模型，如图 2(a)所示；采用 75号壳单元建立伸臂试件的精细模型，划分单元网格时，保证型钢截面的翼缘和腹板不少于8个积分点，同时控制壳单元的长宽比不超过 3，最终建立的精细有限元模型示意如图 2(b)所示；所有的钢材材料属性均根据文献[7-8]中材性试验结果确定.采用宏观和精细模型对 JDA试件的单调和循环加载的试验工况进行模拟，得到其荷载-位移曲线对比如图 3所示.从图中可以看到，在构件未屈服阶段，宏观和精细模型均能较好地模拟试件初始刚度、屈服承载力以及卸载刚度；而当构件屈服后，宏观模型高估了构件的屈服后刚度和卸载刚度，宏观模型的损伤体现为斜腹杆的整体屈服，而试验构件的真实损伤为斜腹杆的波状屈曲和上下弦杆两端的塑性铰[7-8].相比之下，精细模型仍然能较好地预测构件的屈服后刚度和构件的损伤模式(如图 4所示).可见，宏观模型仅能较好地把握构件屈曲前的力学特性，当构件出现屈曲后，宏观模型并不能模拟构件塑性屈曲引起的刚度和承载力退化，而精细模型则能较好地模拟构件弹性、弹塑性至屈曲的全过程.

图2 宏观和精细有限元模型Fig.2 Macro and fine-meshed finite element models

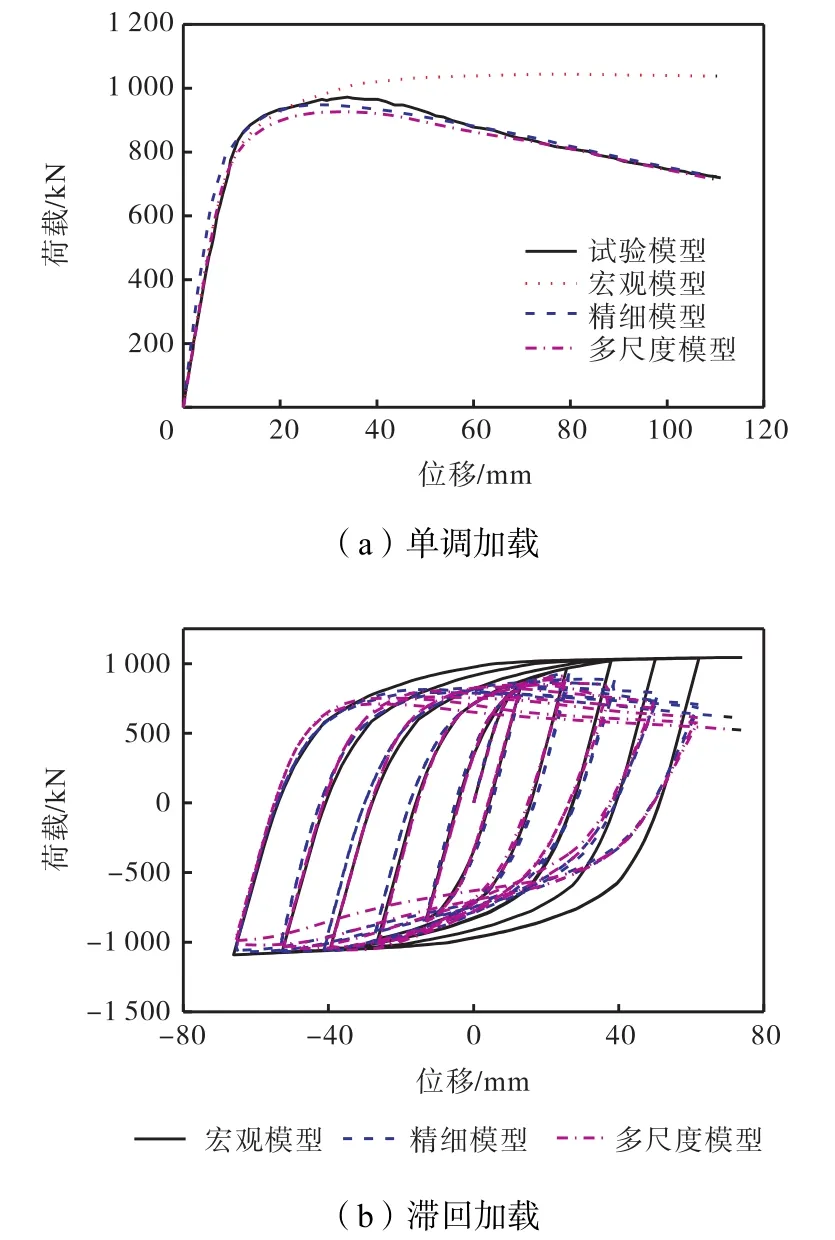
图3 JDA试件单调和滞回加载性能Fig.3 Monotonic and hysteresis characteristics of specimen JDA

图4 JDA试件损伤模式Fig.4 Damage pattern of specimen JDA

1.2 多尺度模型建立

建筑结构的倒塌过程包含了构件从屈服到承载力退化，最后退出工作的全过程，因此，进行倒塌模拟时，所采用的数值模型必须要具备模拟这一过程的能力.从图 3的对比分析可以看出，对于伸臂桁架，宏观模型并不能很好地模拟构件的局部屈曲以及屈曲导致的承载力和刚度退化，可能会对倒塌模拟结果的准确性造成一定的影响.而精细模型能较好地模拟杆件的局部屈曲以及屈曲导致的承载力退化.因此可以考虑采用精细模型来模拟超高层建筑中的伸臂桁架.然而，由于超高层建筑体量巨大，构件数量和种类繁多，即使采用宏观梁单元来模拟伸臂桁架，其有限元模型的单元数量也在 105量级，计算量大且耗时长.如果再采用精细模型来模拟结构中的伸臂桁架，那有限元模型的单元数量将还会增多，建模工作量更大，计算耗时更长.而近年发展起来的多尺度方法则能较好地解决这一问题，它既能模拟构件的微观破坏，也能模拟整体结构的宏观行为，在计算效率和精度之间找到一个很好的平衡点.

JDA试件的试验现象表明，伸臂桁架的最终破坏主要体现为斜腹杆的屈曲破坏，而上下弦杆两端出现塑性铰[7-8].宏观梁单元能较好地模拟构件的弹性响应和压弯破坏，但不能模拟腹板和翼缘的屈曲.因此，在模拟伸臂桁架时，可采用多尺度方法进行建模，对于发生屈曲破坏的斜腹杆，采用基于壳单元的精细模型，网格的划分策略与精细模型一致；对于上、下弦杆和竖杆仍然采用基于梁单元的宏观模型进行模拟.在两种尺度的交界面，采用陆新征等[13]提出的多尺度界面连接技术进行连接，其示意如图 5所示，不同尺度模型之间，仍然满足平截面假定.在MSC.Marc中可方便地使用 REB’2约束关系实现连接界面的位移协调，最终建立的伸臂桁架多尺度模型如图 6所示，需要说明的是，由于斜腹杆两端通过节点板与上、下弦杆以及竖杆连接，且试验表明：在单调和循环往复荷载作用下，节点基本保持弹性或轻微塑性，未出现屈曲现象，仍有一定的安全储备，能实现“强节点，弱构件”的良性失效机制.而斜腹杆的屈曲主要集中在两节点板中间的杆件部分[7-8]，因此，斜腹杆位于节点板中间的部分采用壳单元进行模拟，两端与节点板连接的部分仍采用宏观梁单元进行模拟.

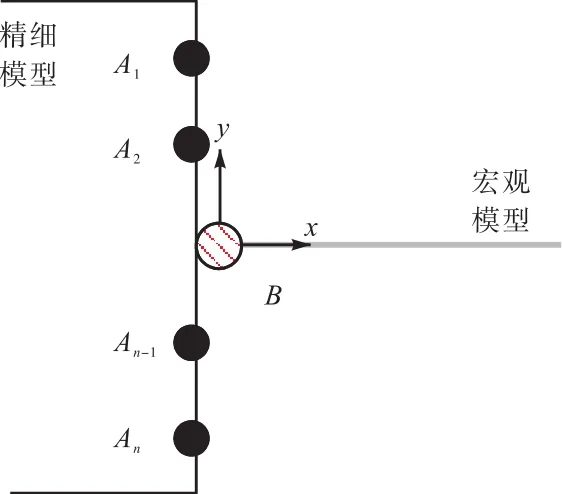
图5 多尺度界面连接示意Fig.5 Connection interface of multi-scale model

图6 JDA试件多尺度模型Fig.6 Multi-scale model of specimen JDA

采用多尺度模型对构件 JDA单调和循环加载试验工况进行模拟，荷载-位移曲线对比如图 3所示.可见，多尺度模型能较好地预测构件的初始刚度、屈服承载力、屈服后刚度、卸载刚度以及滞回耗能等特性.宏观、精细和多尺度模型的滞回分析时间比较如表 1所示.宏观模型的计算效率最高，仅需28.98,s，多尺度模型其次，精细模型最慢.多尺度模型的分析效率比精细模型提高了约6.7倍，而分析精度两者基本一致.因此，可以采用本文所提出的伸臂桁架多尺度建模技术进行整体结构的地震灾变研究.

表1 3个模型的分析时间比较Tab.1 Comparison of analysis times of three models

本文选取上海中心大厦为典型研究对象，该超高层建筑位于上海浦东新区，共124层，总高632,m，其抗侧力体系主要由巨柱-核心筒-伸臂桁架构成.核心筒底部边长约为 30,m，最大墙厚 1.2,m，沿高度逐渐递减至0.5,m；外围由 12根型钢混凝土巨柱组成，底部最大截面约 5.3,m×3.7,m；每道伸臂桁架高约9.9,m，均由H型钢组成[15].文献[15]对其抗震性能及抗倒塌能力进行了分析，但伸臂桁架采用宏观梁单元进行模拟，并未考虑腹杆的屈曲.因此，本文在此基础上，基于伸臂桁架多尺度模型对其抗震性能和抗倒塌性能进行评估，讨论伸臂桁架屈曲对其影响.

由于宏观梁单元能较好地模拟型钢构件的弹性响应和压弯破坏，但不能模拟腹板和翼缘的屈曲，故对于可能发生屈曲的部分宜采用多尺度模型进行模拟.在上海中心大整体结构中，伸臂桁架贯穿外围巨柱，并嵌入到内部核心筒的剪力墙中，其连接关系示意见图 7.对于位于巨柱外侧的伸臂桁架，由于传递的剪力和弯矩非常小，地震荷载作用下基本保持弹性[15]，故对该部分伸臂仍采用宏观梁单元进行模拟；对于嵌入到巨柱和核心筒中的伸臂桁架部分，由于受到混凝土的约束作用，不会发生屈曲，故该部分伸臂也采用宏观梁单元进行模拟；而对于巨柱和核心筒之间的伸臂桁架，传递了绝大部分的轴力、剪力和弯矩，在地震荷载作用下会屈服，因此，对该部分伸臂桁架斜腹杆采用本节提出的多尺度建模技术进行模拟.从试验结果和图 4的分析结果可以看到，伸臂桁架的上、下弦杆主要受力状态为压弯，损伤模式为两端出现塑性铰，故仍采用宏观梁单元模拟伸臂桁架的上、下弦杆.其他构件如巨柱、核心筒和钢框架的模拟方法及单元尺寸划分与文献[15]中上海中心大厦的有限元模型完全一致，巨柱和核心筒采用分层壳单元模拟，钢框架、伸臂桁架等型钢构件采用梁单元进行模拟，最终建立的上海中心大厦整体结构的多尺度有限元模型如图 7所示.值得注意的是，为了后续讨论方便，将文献[15]中采用宏观梁单元模拟伸臂桁架的上海中心整体有限元模型简称为“宏观模型”，而将本文采用多尺度方法模拟伸臂桁架的上海中心整体有限元模型简称为“多尺度模型”.由于伸臂桁架斜腹杆采用了多尺度建模策略，故上海中心大厦整体结构多尺度模型的单元总数增加至 109,700个，而宏观模型的单元总数为 94,068个，增加了约16.6%.

图7 上海中心大厦多尺度模型示意Fig.7 Multi-scale model of Shanghai Tower

2 抗震性能比较

2.1 基本动力特性

了解结构的动力特性是进行结构抗震设计和评估的重要步骤，因此，首先对上海中心大厦的基本动力特性进行分析，宏观模型和多尺度模型的结果及计算效率比较如表 2所示.比较表明：两个模型的自振周期基本一致，前 5阶平动周期的相对偏差均小于0.05%,，说明宏观模型和多尺度模型均能较好地模拟伸臂桁架的初始刚度，这也与第 1节的分析结论一致.因此，在基本动力特性分析阶段，伸臂桁架的宏观模型即能满足整体结构的分析精度需求.在同一计算平台下，宏观模型与多尺度模型前 30阶模态分析总时长分别为440,s和472,s，虽然多尺度模型分析时长增加，计算效率降低，但仅降低约 7.3%,，仍在可接受的范围内.

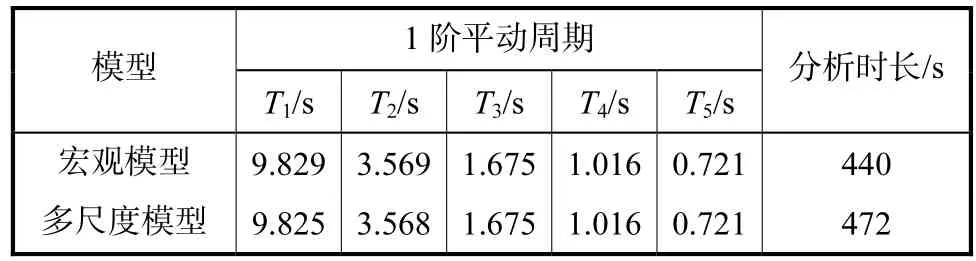
表2 两个模型基本动力特性及计算效率比较Tab.2 Comparison of basic dynamic characteristics and calculation efficiency between two models

2.2 罕遇地震位移响应

初步以科研中广泛采用的El-Centro EW 1940地震动记录为基本输入，将其 PGA调幅至 400,cm/s2(对应于规范中的8度大震水平)，对两个模型进行了弹塑性时程分析，阻尼采用经典的 Rayleigh阻尼，阻尼比取 5%,，两个模型的位移响应比较如图 8所示.可见，两个模型层间位移角包络基本一致，这是由于大多伸臂桁架的斜腹杆均还处于弹性状态(见图9)，没有发生屈曲及由此导致的承载力和刚度退化，因此，在伸臂桁架进入非线性程度较低的阶段，不考虑伸臂桁架的局部屈曲而直接采用宏观梁模型模拟伸臂桁架仍能满足弹塑性分析的精度需求.

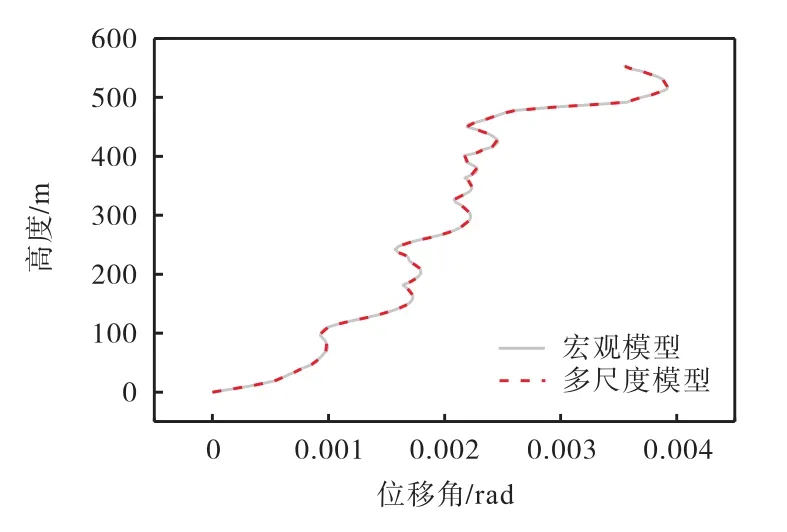
图8 层间位移角包络比较Fig.8 Comparison of envelope of interstory displacement angle

图9 典型伸臂桁架斜腹杆轴力-位移滞回曲线Fig.9 Axial force-displacement hysteresis curve of diagonal brace in typical outrigger

3 地震灾变比较

为研究伸臂桁架的塑性屈曲对上海中心大厦在特大地震下动力灾变过程的影响，仍以El-Centro EW 1940地震动记录为典型输入，采用Lu等[15-16]提出的倒塌模拟方法对上海中心大厦多尺度模型进行倒塌分析，将 PGA 调幅至 1,960,cm/s2，宏观模型和多尺度模型的详细倒塌过程比较如表3所示，其中括号内的时间为多尺度模型对应的构件破坏时间.

从表 3中可以看出，在 3.90,s以前，宏观模型和多尺度模型的损伤发展过程基本一致，均始于伸臂斜腹杆的屈服和连梁的破坏；在 3.90,s以后，在多尺度模型中，第5节段伸臂桁架斜腹杆局部屈曲破坏而退出工作，使得该节段的核心筒和巨柱迅速破坏，进而使第 5节段的竖向承载力逐渐丧失；反观宏观模型，桁架采用宏观梁单元进行模拟，在整个受力过程中无法考虑杆件塑性屈曲，斜腹杆体现为整体屈服(见图10(a))，仍然能参加大量耗能，从而高估伸臂桁架的耗能能力(见图 10(b))，降低了核心筒和巨柱的损伤程度，因此，其倒塌发生的时间略晚于多尺度模型.此外，多尺度模型在第5和6节段的交界处也发生了严重破坏，最终的倒塌体现为第5节段完全折断的竖向倒塌模式；而宏观模型为仅第5节段底部折断的竖向倒塌模式，两个模型的最终倒塌模式如图11所示.

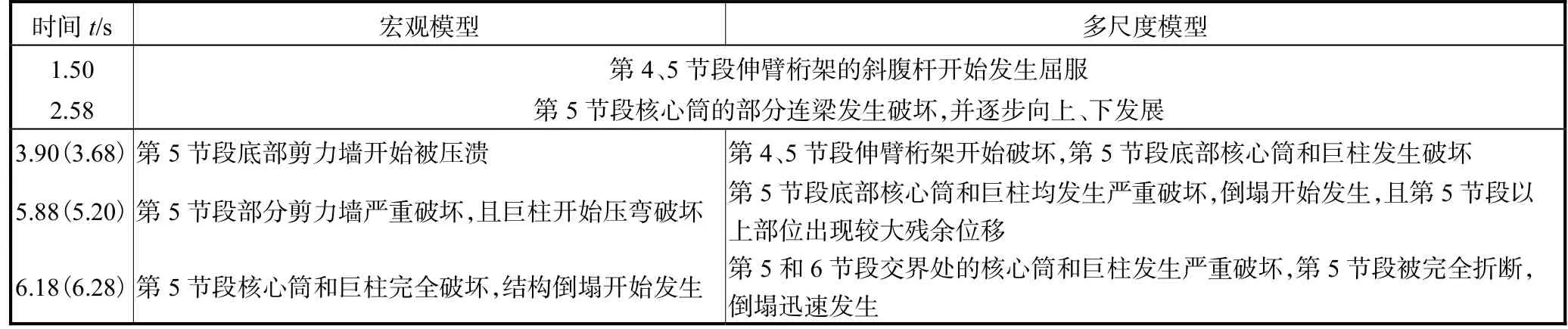
表3 宏观模型和多尺度模型倒塌过程对比Tab.3 Comparison of collapse process of macro and fine-meshed models

倒塌过程中，两个模型顶点的水平和竖向位移时程如图 12所示，从水平位移时程可以看出，多尺度模型在第5节段巨柱和核心筒开始破坏后，第5节段上部出现了一定程度的倾覆；竖向位移时程也表明，多尺度模型的倒塌开始时间略早于宏观模型.倒塌发生时刻两个模型加强层处的水平位移及节段间水平位移角(上下节段位移差除以节段高度)如图13所示.可见，虽然两个模型的倒塌时刻的振动方向相反，但结构变形模式均呈高阶振型(水平3阶振型)形状.多尺度模型第6、7、8节段出现了明显的倾覆，由于其重心的水平位移并不太大，重力产生的倾覆力矩还不足以使上部节段出现倾覆的倒塌模式.

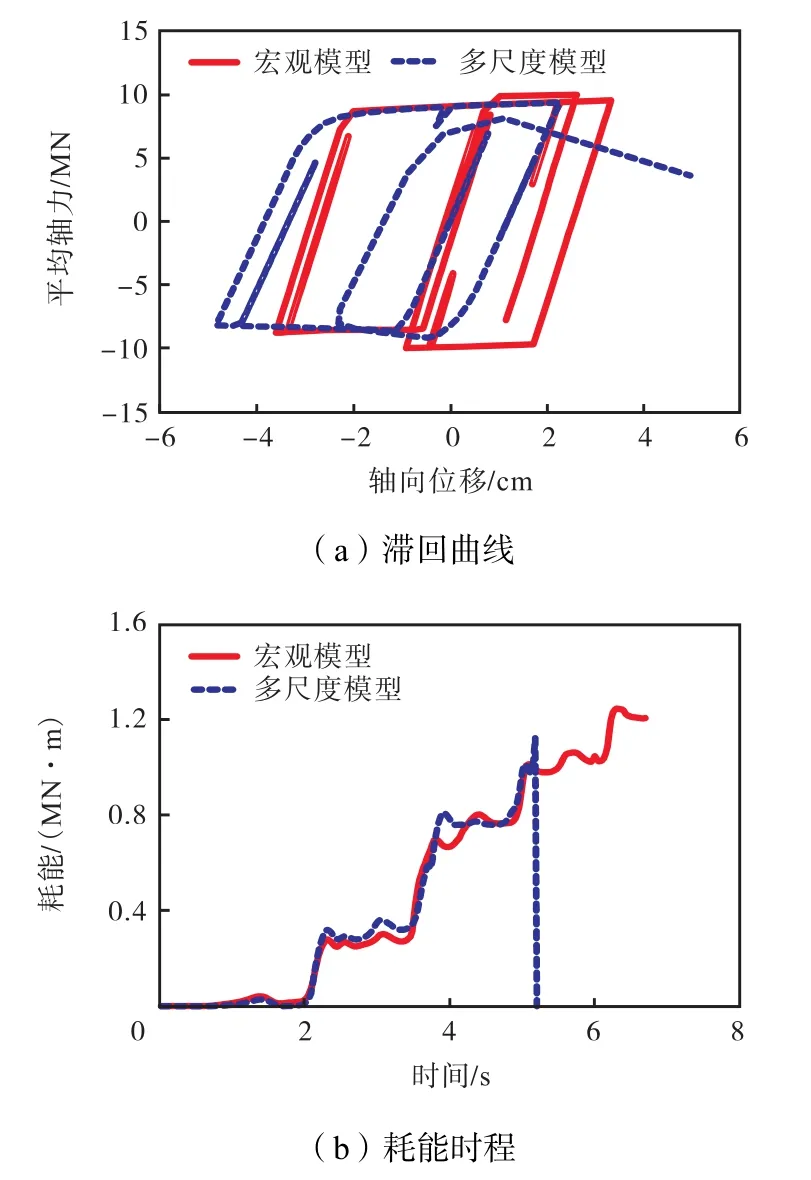
图10 典型斜腹杆滞回曲线及耗能时程对比Fig.10 Hysteretic curve and energy dissipation history of diagonal brace in typical outrigger

图11 两个模型的典型倒塌模式Fig.11 Typical collapse modes of two models

图12 倒塌过程中结构顶点水平和竖向位移时程Fig.12 Horizontal and vertical displacements histories incollapse process

图13 倒塌临界状态时的节段位移响应Fig.13 Displacement responses of each segment in critical collapse state

为进一步探讨伸臂桁架塑性屈曲对抗倒塌能力的影响，采用逐步增量分析方法确定多尺度模型的临界倒塌地震强度.当 El-Centro EW,1940地震动的PGA调整至 1,568,cm/s时，多尺度模型发生临界倒塌；而宏观模型的在 El-Centro EW,1940地震动下的临界倒塌强度为 1,764,cm/s2.可见，在 El-Centro EW,1940地震动作用下，不考虑伸臂桁架的塑性屈曲可能会高估结构12.5%,的抗倒塌能力.

总的说来，是否考虑伸臂桁架的塑性屈曲对倒塌的初始损伤部位和次序没有明显影响，但伸臂桁架发生塑性屈曲后，对其倒塌损伤演化过程以及抗倒塌能力均有明显影响.采用宏观梁单元模拟伸臂桁架，不能模拟伸臂桁架的塑性屈曲，会高估伸臂桁架的地震耗能，进而低估核心筒和巨柱的损伤程度，最终影响结构的倒塌模式和抗倒塌能力.因此，对于带有伸臂桁架超高层建筑的地震灾变模拟，宜考虑伸臂桁架的塑性局部屈曲效应，使预测的倒塌过程和抗倒塌能力更加准确.

4 结 论

(1) 宏观梁单元仅能较好预测伸臂桁架的初始刚度和屈服承载力，不能模拟塑性屈曲引起的承载力和刚度退化，而本文提出的伸臂桁架多尺度模拟能较好地模拟伸臂桁架的初始刚度、屈服承载力以及塑性屈曲引起的承载力和刚度退化，且具有较高的计算效率.

(2) 在伸臂桁架屈服前，仍然可以采用宏观梁单元模拟伸臂桁架进行超高层建筑整体结构动力特性分析和地震响应预测.

(3) 在进行超高层建筑地震灾变全过程模拟时，应考虑伸臂桁架的塑性屈曲，可采用多尺度模型模拟伸臂桁架.采用宏观模型会高估伸臂桁架的塑性耗能，低估核心筒和巨柱的损伤程度，高估结构的抗倒塌能力.在典型El-Centro EW1940地震动作用下，不考虑伸臂桁架的塑性屈曲可能会高估结构 12.5%,的抗倒塌能力.

此外，本文仅以典型地震动记录定性讨论了伸臂桁架塑性屈曲对抗倒塌能力的影响，由于地震动记录的频谱成分有较大的不确定性，在后续研究中，还将选取更多的地震动记录进一步讨论伸臂桁架塑性屈曲对超高层建筑抗倒塌性能的影响.

：

［1］ Li Q S，Zhi L H，Tuan A Y，et al. Dynamic behavior of Taipei 101 tower：Field measurement and numerical analysis[J].Journal of Structural Engineering，2010，137(1)：143-155.

［2］ Yang Y，Wang P，Wang J，et al. Seismic analysis of the hung curtain wall structure in Shanghai Center Tower[J].The Structural Design of Tall and Special Buildings，2013，22(11)：847-861.

［3］ Lu X Z，Lu X，Guan H，et al. Earthquake-induced collapse simulation of a super-tall mega-braced framecore tube building[J].Journal of Constructional Steel Research，2013，82：59-71.

［4］ Lu X L，Chen Y，Mao Y. Shaking table model test and numerical analysis of a super-tall building with high-level transfer story[J].The Structural Design of Tall and Special Buildings，2012，21(10)：699-723.

［5］ Shamass R，Alfano G，Guarracino F. A numerical investigation into the plastic buckling paradox for circular cylindrical shells under axial compression[J].Engineering Structures，2014，75：429-447.

［6］ Ghazijahani T G，Jiao H，Holloway D. Plastic buckling of dented steel circular tubes under axial compression：An experimental study[J].Thin-Walled Structures，2015，92：48-54.

［7］ 赵宪忠，王 斌，陈以一，等. 上海中心大厦伸臂桁架与巨柱和核心筒连接的静力性能试验研究[J]. 建筑结构学报，2013，34(2)：20-28.Zhao Xianzhong，Wang Bin，Chen Yiyi，et al. Monotonic static tests on outrigger truss and its connection with mega column and core tube of the Shanghai Tower[J].Journal of Building Structures，2013，34(2)：20-28(in Chinese).

［8］ 陈以一，王 斌，赵宪忠，等. 上海中心大厦伸臂桁架与巨柱和核心筒连接的抗震性能试验研究[J]. 建筑结构学报，2013，34(2)：29-36.Chen Yiyi，Wang Bin，Zhao Xianzhong，et al. Hysteretic tests on outrigger truss and its connection with mega column and core tube of the Shanghai Tower[J].Journal of Building Structures，2013，34(2)：29-36(in Chinese).

［9］ 赵秋红，李 楠，孙军浩. 波纹钢板剪力墙结构的抗侧性能分析[J]. 天津大学学报：自然科学与工程技术版，2016，49(增1)：152-160.Zhao Qiuhong，Li Nan，Sun Junhao. Analysis on lateral performance of sinusoidally corrugated steel plate shear walls[J].Journal of Tianjin University：Science and Technology，2016，49(Suppl1)：152-160(in Chinese).

［10］ Salvatore W，Bursi O S，Lucchesi D. Design，testing and analysis of high ductil e partial-strength steelconcrete composite beam-to-column joints[J].Computers & Structures，2005，83(28)：2334-2352.

［11］ Han L H，Wang W D，Zhao X L. Behaviour of steel beam to concrete-filled SHS column frames：Finite element model and verifications[J].Engineering Structures，2008，30(6)：1647-1658.

［12］ Li Z X，Zhou T Q，Chan T H T，et al. Multi-scale numerical anal ysis on dynamic response and local damage in long-span bridges[J].Engineering Structures，2007，29(7)：1507-1524.

［13］ 陆新征，林旭川，叶列平. 多尺度有限元建模方法及其应用[J]. 华中科技大学学报：城市科学版，2008，25(4)：76-80.Lu Xinzheng，Lin Xuchuan，Ye Lieping. Multiscale finite element modeling and its application in structural analysis[J].Journal of Huazhong University of Science and Technology：Urban Science Edition，2008，25(4)：76-80(in Chinese).

［14］ 潘建荣，杨正挺，王 湛，等. 基于多尺度的半刚性组合框架抗震性能数值分析[J]. 天津大学学报：自然科学与工程技术版，2016，49(增1)：161-167.Pan Jianrong，Yang Zhengting，Wan Zhan，et al. Numerical analysis of seismic behavior of semi-rigid composite frame on multi-scale[J].Journal of Tianjin University：Science and Technology，2016，49(Suppl1)：161-167(in Chinese).

［15］ Lu X，Lu X Z，Zhang W K，et al. Collapse simulation of a super high-rise building subjected to extremely strong earthquakes[J].Science China Technological Sciences，2011，54(10)：2549-2560.

［16］ Lu X，Lu X Z，Guan H，et al. Collapse simulation of reinforced concrete high rise building induced by extreme earthquakes[J].Earthquake Engineering & Structural Dynamics，2013，42(5)：705-723.