用于二维分布残余应力场测量的渐进裂纹柔度法
2018-05-18陈金龙尹承振孙翠茹
陈金龙 ,尹承振,孙翠茹
(1. 天津大学机械工程学院,天津 300350;2. 天津市现代工程力学重点实验室,天津 300350)
金属工件在热处理过程中会出现由于温度的不均匀分布以及显微组织变化而引发的体积和形状改变,从而其内部产生复杂分布的残余应力[1].尤其在采用焊接工艺对金属工件进行加工时,由于焊接过程中的局部高温、冷却收缩及金属相变等因素,工件内部必然产生残余应力,且在工件横截面内残余应力全场分布复杂、分布均匀性差[2-3].例如,在深海水下油气输送系统中,输油管道通常采用焊接工艺加工而成,存在于焊件横截面内的残余应力通常沿厚度和宽度方向同时变化,呈二维分布形式[4-5].在管道服役过程中,其复杂分布的残余应力与工作应力相互叠加,极易导致输油管道出现疲劳破坏、变形开裂等损伤,造成油气泄漏,甚至进一步导致严重事故[6].因此,工件内部的焊接残余应力对于工件的力学性能、服役寿命以及整个机械系统的安全性有重要影响,有必要准确测量工件横截面内全场残余应力的大小及分布.
焊接残余应力测量方法主要分为无损检测和有损检测.对于无损检测,工程中常用的方法有X射线法以及中子衍射法等.例如,杨峰等[7]利用 X射线法测量技术对2205双相不锈钢焊接界面残余应力进行测试,研究了摩擦焊接头区域残余应力分布规律;蒋文春等[8]利用中子衍射分析了不锈钢复合板补焊残余应力.而对于有损检测,常用方法包括成熟的盲孔法[9]、较新的裂纹柔度法[10]及轮廓法[11]等.然而,上述方法中,X射线法只能测量工件表面残余应力,盲孔法只能获得工件局部区域内的残余应力;而裂纹柔度法虽然可以得到工件内沿厚度方向分布的一维残余应力场,但该方法要求工件横截面内残余应力场需沿其宽度方向均匀分布[12],因而不适用于测量工件横截面内二维分布残余应力场.目前,中子衍射法和轮廓法均可以获得工件横截面内呈二维分布的残余应力场.然而,中子衍射法中子源的流强较弱,测量时间长,中子源建造和运行费用昂贵,测量成本较高[13];轮廓法所用测量工具要求较高,被测材料种类有限[14],而且不能直接获得二维分布残余应力场的数学表达式.因此,工程上要求发展新的残余应力测量方法,在克服中子衍射法与轮廓法测量技术不足的同时,可以准确获得工件横截面内二维分布残余应力的大小及分布.
为满足上述需求,笔者基于传统裂纹柔度法的理论与实验方法,利用反问题分析原理,提出了传统裂纹柔度法的改进方法——渐进裂纹柔度法.通过理论分析及数值模拟研究,详细阐述了渐进裂纹柔度法测量二维分布残余应力场的方法实现过程,为该方法的进一步发展和完善奠定了基础.
1 渐进裂纹柔度法理论研究
1.1 基本假定与模型建立
在裂纹柔度法基础之上,渐进裂纹柔度法是指在被测物体的表面引入一条宽度“渐进”且深度逐渐增加的裂纹来释放残余应力,并通过测量对应不同裂纹长度和深度下的指定点处的应变值或位移值来反算残余应力的方法.与裂纹柔度法相比,渐进裂纹柔度法的人为引入裂纹长度和深度同时逐渐增加,每次通过切割释放单个小方形区域内残余应力,以此来达到测量被测物体内横截面二维分布残余应力场的目的.其中,裂纹柔度法与渐进裂纹柔度法原理对比如图1所示.
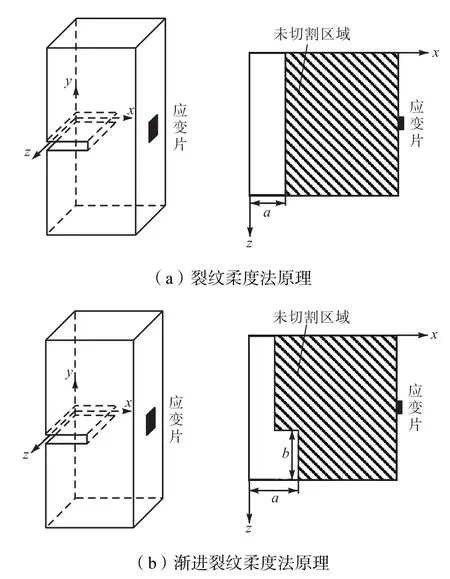
图1 裂纹柔度法与渐进裂纹柔度法测量原理比较Fig.1 Comparison of principle diagram of slitting method and incremental slitting method
为准确测量二维分布残余应力场,渐进裂纹柔度法应满足以下基本假设:①在待测横截面内,残余应力沿材料厚度方向和宽度方向可以同时变化,且可表示为空间坐标的二元连续函数形式;②被测材料为线弹性材料,并在测量过程中保持线弹性性质;③所测指定点的应变仅由垂直于裂纹面的残余正应力的释放而产生,不考虑或忽略其他方向上的正应力以及切应力;④切割过程中不产生附加应力,或附加应力很小从而不予考虑.事实上,与裂纹柔度法的基本假设相比,渐进裂纹柔度法只改变了裂纹柔度法基本假设中的沿工件宽度方向均匀分布假设.
根据上述基本假设,基于裂纹柔度法中释放残余应力与相应的释放应变之间的关系[15],在渐进裂纹柔度法中,可将残余应力 σy与释放应变 εy表示为第1类二维Volterra积分方程形式[16],即

式中:a为切割深度;b为切割宽度;KL为与材料性质、形状等有关的核函数;下标 L为应变片位置标记符号.
根据多元函数展开理论,可将残余应力 σy(x,z)表示为二元基函数级数形式[17],即
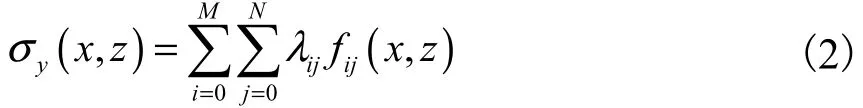
式中:λij为多项式系数;fij(x,z)代表二元基函数;M、N为指定的二元函数展开阶数.
将式(2)代入到式(1)中,并将 a、b分别离散化为 xr、zq,可以得到
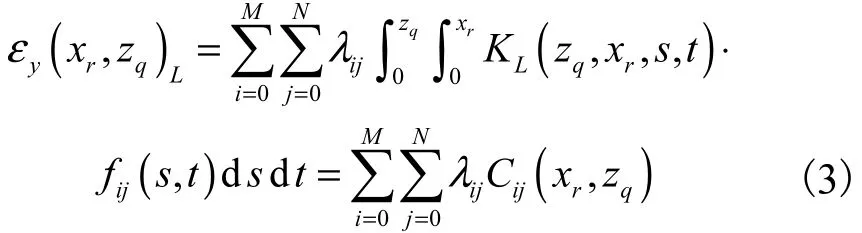
式中:r=1,2,…,R;q=1,2,…,Q;R 和 Q 分别代表厚度方向与宽度方向切割次数,同时应满足 R>M,Q>N,且当 q=Q 时,裂纹延伸到试件的整个宽度,形成贯穿裂纹;Cij(xr,zq)为渐进裂纹柔度函数,为四元变量函数,其含义为

即当残余应力分布形式为二元函数 fij(x,z),且裂缝切割深度a为xr、切割宽度b为zq时,指定点处释放应变的大小.
为简便起见,可将式(3)改写为

式中:εrq为实验得到的释放应变数据;Cijrq为渐进裂纹柔度函数,可通过有限元法计算得到.λij为待求待定系数,因此,在求解式(5)之前,必须先选取二元基函数 fij(x,z)以及计算相对应的渐进裂纹柔度函数Cijrq.下面分别详述fij(x,z)的选取以及Cijrq的计算方法,最后介绍利用反问题分析原理中的正则化方法求解λij.
1.2 二元基函数的选取
为满足基函数系的完备性与连续性,以及计算简单和方便,在裂纹柔度法中常常采用正交多项式作为未知残余应力展开式的基函数.而在渐进裂纹柔度法中,二元基函数fij(x,z)可以采用多种形式.为计算简单和方便,本文采用二维方体域[-1,1]×[-1,1]上的正交多项式——二元勒让德多项式作为基函数[18],即

式中Pi(x)与Pj(z)均为一元勒让德多项式.
由于残余应力是自平衡的,因而在待测截面上σy(x,z)需要满足力平衡和力矩平衡条件.而在二元勒让德多项式系中,除 f00(x,z)、f01(x,z)和 f10(x,z)三项外,其余各项经过统一的坐标变换后,均能自动满足平衡条件.因此,可以将式(2)所表示的待测残余应力二元展开式中的 λ00、λ01、λ10均设置为 0.
1.3 渐进裂纹柔度函数Cijrq的计算
裂纹柔度法中,裂纹柔度函数可以利用体力法、断裂力学解析法以及有限元法或其他数值方法进行求解.在渐进裂纹柔度法中,由于假设残余应力分布函数为二元函数,函数形式十分复杂,且切割方式也与裂纹柔度法明显不同,因此采用解析法求解Cijrq难度极大.与解析法相比,有限元法作为一种常用的数值计算方法,具有求解速度快、精度高且适用于复杂形状的构件等特点,故而在渐进裂纹柔度法中,采用有限元法来计算渐进裂纹柔度函数.本文采用ABAQUS 6.14有限元软件进行计算工作,其模型(图2所示)以及简要计算步骤如下所述.

图2 求解Cijrq有限元模型示意Fig.2 Schematic illustration of finite element model for solving Cijrq
首先,如图 2所示,采用三维模型,根据被测试件的对称性,仅需以待切割的平面作为对称面,将半个试件网格化,选用 C3D8R单元,并对对称面附近网格间距进行细化.在对称面上施加对称约束,棱边AB施加 x方向与 z方向位移约束,以防止发生刚体位移.设置材料的弹性模量 E=1,GPa,泊松比为0.33.然后,编写用户子程序 DLOAD,将各阶二元基函数(式(6))分别作为初始应力载荷施加到对称面上.在模型上通过对裂缝处单元的去除来模拟裂纹的渐进扩展:在某一切割深度 a=xr下,切割宽度 b分别为 z1,z2,…,zQ,共切割 R·Q 次.同时,记录每次切割后模型底部指定点处的应变数据.最终,当模拟切割深度达到归一化厚度 0.9时,停止计算,整理数据,从而得到渐进裂纹柔度函数Cijrq.
1.4 待定系数λij的求解
在选定二元基函数 fij(x,z)以及计算出渐进裂纹柔度函数 Cijrq后,即可以利用实验应变数据 εrq求解式(5)进而得到λij.首先,为计算方便,可将式(5)的各个参量进行降维处理,变换为线性方程组的形式,即

其中
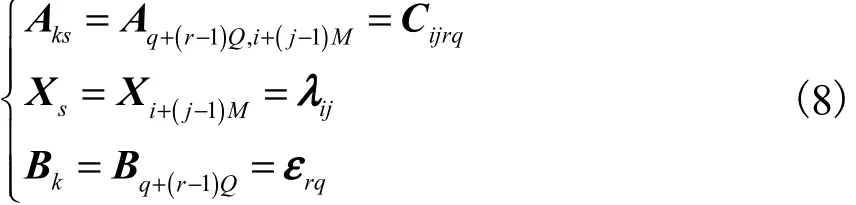
式中:Aks为矩阵;Xs与 Bk均为一元列向量.降维过程实际上是对数据的一种重新排列,最终形成线性方程组以方便计算,同时不改变原方程的本质.
对于线性方程组式(7),裂纹柔度法中常常采用最小二乘法求解.在系数矩阵 Aks的条件数较小时(裂纹柔度法中,cond通常小于 101),采用最小二乘法求解式(7)是可行的.然而,当系数矩阵 Aks的条件数很大时(渐进裂纹柔度法中,可能会大于 1014),矩阵 Aks病态性较为严重,此时该方程组的最小二乘解是发散的,因此需要采用其他适当方法求解该病态方程组.同时,利用裂纹柔度法测量二维分布残余应力场亦属于反问题分析.在反问题分析中,常常采用正则化方法来消除病态系数矩阵对计算结果的影响.因此,本文采用反问题分析中常用的Tikhonov正则化方法求解线性方程组式(7),其求解公式为
式中:α为正则化参数;I为单位矩阵.
正则化参数 α的选取对问题解的性态有重要作用,而且有多种选取方法.本文采用L曲线法[19]获得近似最优的参数α.
求得 Xs后,根据式(8)将其转换为矩阵形式的待定系数 λij.最终,将所求得的待定系数 λij带回到式(2)中,即可得到待测工件横截面内二维分布残余应力场表达形式.
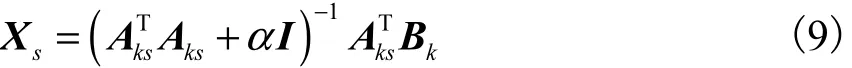
2 渐进裂纹柔度法算法验证
2.1 有限元仿真施加残余应力
高斯分布应力是一种常见的残余应力,其特点为工件表面附近为压应力,而厚度中心为拉应力.此类残余应力场可以通过表面喷丸强化、激光喷丸强化、表面硬化或其他表面处理工艺获得[20].由于高斯分布应力的分布形式较为复杂,其相应的展开级数收敛性差,因此常常被应用于传统裂纹柔度法算法验证实验中.为不失一般性,本文采用有限元仿真实验法,利用本文提出的渐进裂纹柔度法,测量沿厚度方向呈高斯分布、沿宽度方向呈一般多项式分布的横截面二维分布残余应力场来验证该方法的可行性和有效性.
在有限元软件ABAQUS 6.14中,建立工件三维模型(模型尺寸为 4×1×1,为代表一般性,进行无量纲化处理),其中,x方向与z方向坐标范围均设置为[0,1] .设置材料的弹性模量为 1,GPa,泊松比为0.33.在该试件模型的对称横截面上施加二维分布的残余应力场(单位:MPa)为

式(11)为高斯分布应力表达式,其分布如图3(a)所示.式(12)为一般多项式分布应力,代表残余应力沿宽度变化时的一般情况,其分布如图 3(b)所示.为不失一般性,本文将两种分布形式的残余应力场峰值进行了归一化处理,即最大残余应力为单位应力 1,MPa.同时,σy(x,z)在整个截面内的积分以及对x轴与z轴的1阶矩均小于10-6,因此可以认为该残余应力场自动满足自平衡条件.将 σy(x,z)所表示的残余应力场施加到模型横截面上后,该残余应力场分布如图 4所示,中间区域为拉应力,且具有单峰值;左右两侧区域为压应力,且在 x=0.1附近变化较为剧烈.
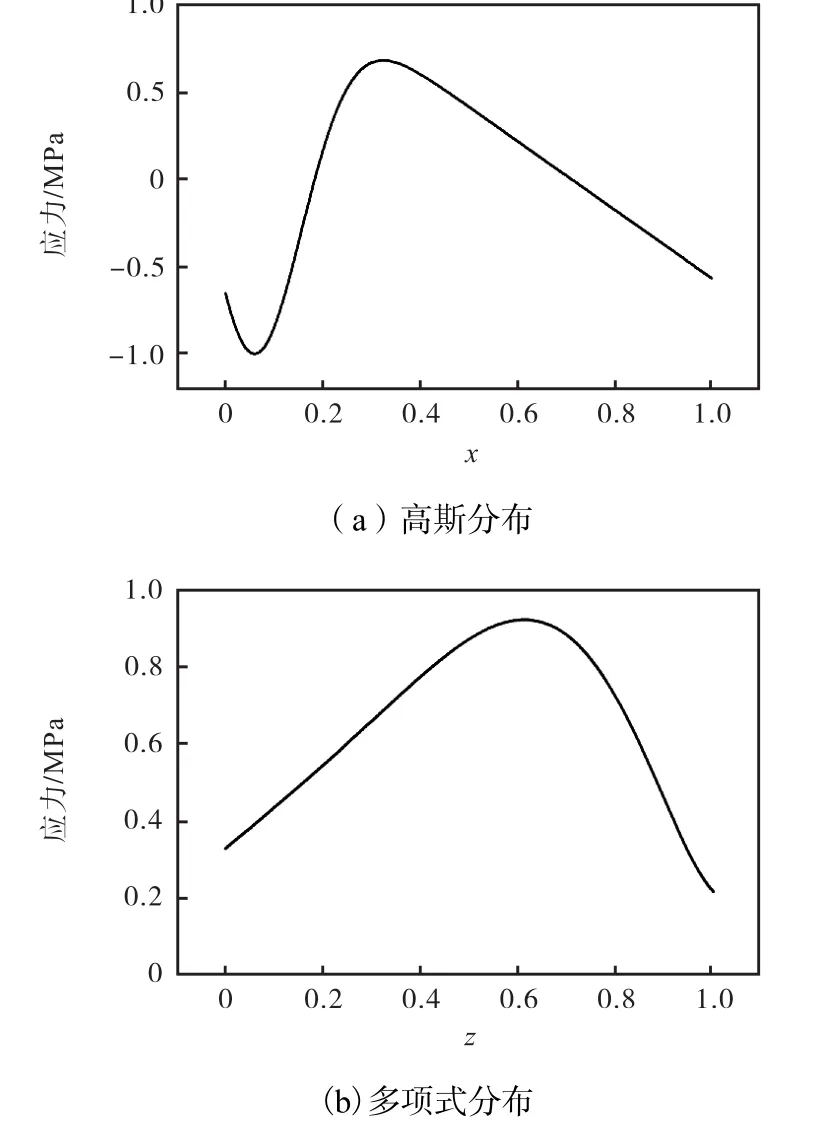
图3 高斯分布与多项式分布曲线Fig.3 Graph of Gaussian distribution and polynomial distribution
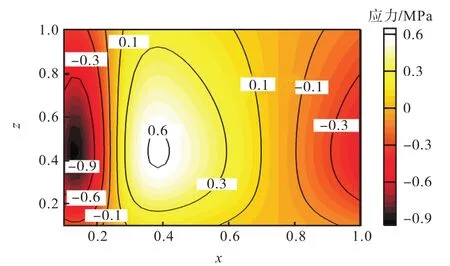
图4 给定二维分布残余应力场Fig.4 Given two-dimensional mapping of residual stress field
2.2 渐进裂纹柔度法测量残余应力
利用本文提出的渐进裂纹柔度法对此试件的残余应力场进行测量.根据模型的对称性,沿对称面将试件切割成2等份,建立试件长度方向尺寸1/2的模型,并在对称面上施加与图 2所示相同的约束,裂纹面上施加图4所示的二维分布残余应力场.
2.2.1 有限元模拟释放应变
通过单元去除技术来模拟实际裂纹引入工艺(如铣削加工等)过程,其中,工件深度方向(x方向)共切割 15次,最大切割深度为 0.9.对于每一给定的裂纹深度,裂纹宽度方向(z方向)进行10次平均切割,且为完全切割;最终,总共切割 150次.同时记录每次切割后试件底部待测点(如到对称面距离为 0.075)处的位移数据,然后利用位移值求解得到应变值如图 5所示.从图 5中可以看出,在每次切割后,所释放的应变总体呈递增趋势:在前 40次切割时,变化较为剧烈,且这一过程主要释放压应力;之后,随着拉应力逐步释放,释放应变曲线逐渐平缓;在最后阶段,释放应变具有明显波动.
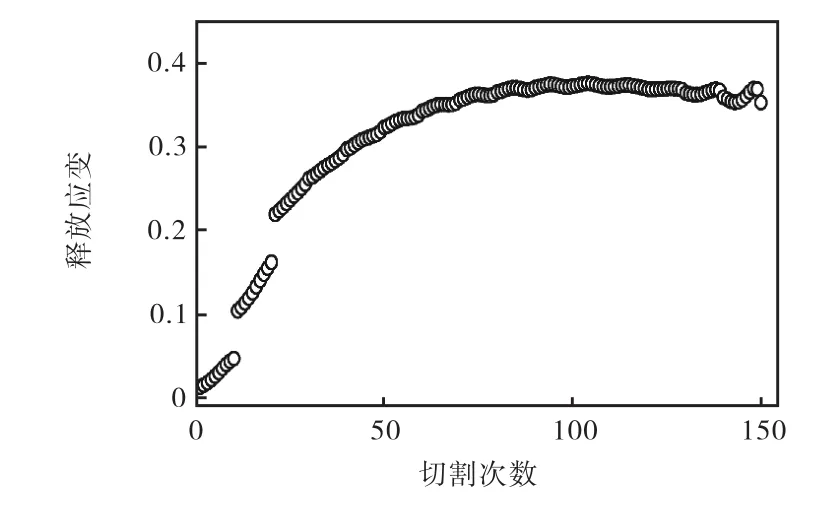
图5 切割过程中的释放应变Fig.5 Released strain data in the process of cutting
2.2.2 二维分布残余应力场求解
首先利用式(2),将残余应力分布表示为 x方向的 12阶勒让德多项式和 z方向的 9阶勒让德多项式,即在式(2)中选取 M=12,N=9.然后,利用 L曲线法求得正则化参数α=3.72×10-5.再将参数 α代入到式(9)中,并利用所得到的释放应变数据,及前文所求得的渐进裂纹柔度函数 Cijrq求得待定系数λij.最后,将待定系数λij代入残余应力二元展开函数式(式(2))中,获得被测物体截面的二维分布残余应力场如图6所示.

图6 测量二维分布残余应力分布场Fig.6 Measured two-dimensional mapping of residual stress field
比较图4与图6,计算测量残余应力场与给定残余应力场的相对误差

式中:Re为相对误差;σcal为测量残余应力场;σgiv为给定残余应力场.计算结果如图7所示.
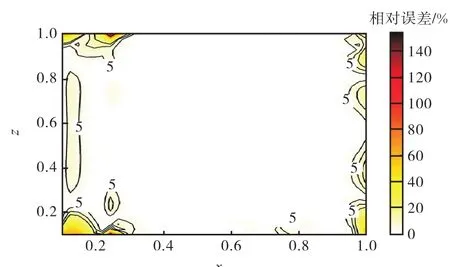
图7 相对误差分布Fig.7 Distribution of relative error
从图 7可以看出,在所给定的测试区域中,中间大部分区域的误差几乎为 0.误差较大的区域主要集中在 x<0.1以及 x>0.9边缘范围内.分别在测试区域中选取 x=0.2、x=0.5、x=0.8 以及 z=0.2、z=0.5、z=0.8六条路径,绘制出沿路径分布的测量残余应力与给定残余应力的对比图,如图8与图9所示.
从图8及图9所示的对比结果可以进一步看出,在不同横向与纵向路径下,测量残余应力与给定残余应力的拟合度极高.所以,渐进裂纹柔度法测量残余应力场与给定残余应力场吻合度非常高,特别是中间区域结果的准确度很高,仅在四周部分区域内存在较大误差.
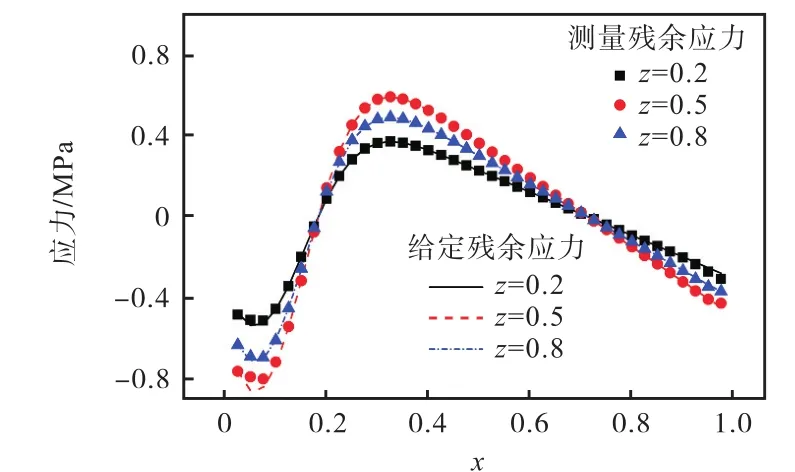
图8 沿水平路径的给定残余应力与测量残余应力对比Fig.8 Comparison of the given residual stress and the measured residual stress along horizontal paths
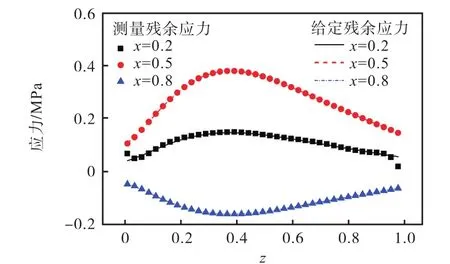
图9 沿纵向路径的给定残余应力与测量残余应力对比Fig.9 Comparison of the given residual stress and the measured residual stress along vertical paths
2.3 应变测量误差对计算结果的影响
前述模拟实验验证过程中,应变模拟测量数据均为精确数值,不含随机误差.在渐进裂纹柔度法实际测量中,由铣削、激光等加工工艺引入“渐进”裂纹,并且采用应变片等技术测量释放应变,极易产生随机误差.下面通过对应变模拟测量值施加不同水平的随机误差,研究应变测量误差对残余应力测量结果的影响.
假定应变测量误差为高斯噪声,即所施加随机误差服从均值为零的正态分布.根据模拟应变的最小值0.013,设置 4个应变随机误差水平Ⅰ、Ⅱ、Ⅲ、Ⅳ,相应的标准差分别为0.001、0.005、0.010和0.020.将此4种误差分别添加到图5的模拟测量应变中,然后计算得到相应的二维分布残余应力场,如图10所示.
由图 10可以发现,当所施加应变随机误差逐渐增大时,给定残余应力场与测量残余应力场的吻合度逐渐降低.同时,计算结果在试件内部区域准确度较高,边缘附近准确度较差,与无应变随机误差条件下的计算结果规律相同.用应力绝对误差的均方根值,量化随机误差对测量结果的影响为

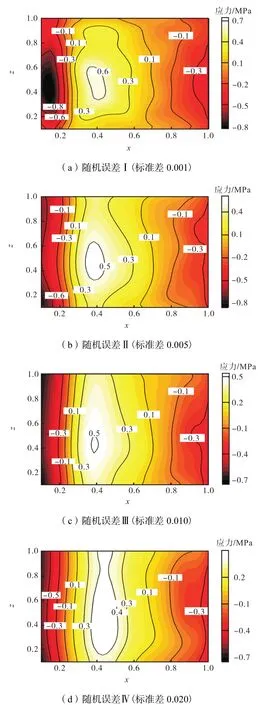
图10 不同应变随机误差水平下的测量二维残余应力场Fig.10 Measured two-dimensional mapping of residual stress in different levels of random error of strain
式中:代表绝对误差均方根;I、J分别代表 x方向与z方向计算点的数目.计算结果如图11所示.

图11 不同应变随机误差水平下的残余应力绝对误差均方根Fig.11 Root-mean square of absolute error of residual stress in different levels of random error of strain
根据图10与图11可以发现,当应变随机误差的标准差不大于0.01时,应力绝对误差的均方根较小,此时的计算结果基本能反映出原残余应力场的大小及分布形式;当随机误差的标准差大于0.01时,应力绝对误差的均方根较大,此时的计算结果失真度较为严重,误差大.
3 讨 论
从图7和图10可以看出应变测量误差较小时,渐进裂纹柔度法可以准确获得工件横截面内二维分布残余应力的大小和分布.而在实际工程测试中,利用应变片测量释放应变时的精度是有限的(一般为1,με),因此所测应变数据存在“截断误差”;其次,由于实验环境和操作不当等外界因素的存在,所测应变数据存在“随机误差”.应变测量误差的传递会造成残余应力场计算误差的增大.另外,渐进裂纹柔度法假设将未知的二维分布残余应力场表示为二元多项式级数形式,其展开阶数的选择会影响计算精度.
然而,模型假设的二维分布残余应力场展开阶数与切割次数及应变片固有测量精度之间是相互影响的:展开阶数越高,则所需切割次数越多,进而残余应力单次释放量越小,应变测量误差可能就越大;反之,展开阶数越小,则可能造成展开阶数与残余应力场函数的真实阶数越不匹配,因而误差会越大.所以在实际工程应用中,应根据实验条件和对待测残余应力场分布形式的预估来确定二元分布残余应力场函数的展开阶数与所需切割次数,以期达到较高的测量与计算精度.总之,渐进裂纹柔度法优势在于对试件内部区域的残余应力场测试准确度高.边缘误差虽然可能较大,但是不影响内部区域的计算精度,因而不影响该方法的准确性与可行性.
渐进裂纹柔度法是一种有损检测方法,在检测残余应力时会完全破坏工件.利用该方法测量获得试件内部横截面上的二维分布残余应力后,可以指导工件的成批加工、制造和装配等.
4 结 论
(1) 本文提出了渐进裂纹柔度法的完整理论模型,以及相应的参数计算方法和方程求解方法,为工件横截面内二维分布残余应力场的测量提供了一种新的方法.
(2) 渐进裂纹柔度法的计算结果在测试区域内部具有较高准确度.由于模型和应变测量误差造成的计算应力边缘失真不影响内部区域的计算精度,因而对于工件内部区域残余应力场的测量具有巨大优势.
(3) 利用渐进裂纹柔度法测量残余应力时,可以采用铣削、锯切以及激光切割等工艺实现“渐进”切割,因而与传统裂纹柔度法相比,该方法对于残余应力在宽度方向上的变化具有更高的灵敏度,适用于金属、非金属以及复合材料工件内部残余应力场的测量.同时,该方法还具有操作简单、可以直接得到工件内部二维分布残余应力场的准确数学表达式等优点.
渐进裂纹柔度法能够提供比传统方法更准确的内部残余应力分布,可广泛应用于工件性能测试、可靠性测试,如产品抽查测量和质量评估等,因而具有较高的工程实用性和广阔的应用前景.
:
[1] 任泉庄,黄 峰,郭正洪. 中碳淬火-配分钢中的残余应力分布[J]. 金属热处理,2016,41(10):1-5.Ren Quanzhuang,Huang Feng,Guo Zhenghong.Distribution of residual stress in medium carbon quenching-partitioning steel[J].Heat Treatment of Metals,2016,41(10):1-5(in Chinese).
[2] 李 霄,熊庆人,石 凯,等. 焊管残余应力研究进展及展望[J]. 焊管,2009,32(7):12-17.Li Xiao,Xiong Qingren,Shi Kai,et al. Research progress and prospect of residual stress in welded pipe[J].Welded Pipe and Tube,2009,32(7):12-17(in Chinese).
[3] Xu W,Liu J,Zhu H. Analysis of residual stresses in thick aluminum friction stir welded butt joints[J].Materials & Design,2011,32(4):2000-2005.
[4] Woo W,An G B,Kingston E J,et al. Throughthickness distributions of residual stresses in two extreme heat-input thick welds:A neutron diffraction,contour method and deep hole drilling study[J].Acta Materialia,2013,61(10):3564-3574.
[5] Liu C,Yi X. Residual stress measurement on AA6061-T6 aluminum alloy friction stir butt welds using contour method[J].Materials & Design,2013,46:366-371.
[6] 杨树贵. 关于焊接钢管残余应力的思考[J]. 焊管,1998,21(2):12-16.Yang Shugui. The residual stress in welded pipes[J].Welded Pipe and Tube,1998,21(2):12-16(in Chinese).
[7] 杨 峰,石端虎,陆兴华,等. 2205不锈钢摩擦焊接头组织及残余应力分布[J]. 金属热处理,2016,41(12):38-41.Yang Feng,Shi Duanhu,Lu Xinghua,et al.Microstructure and residual stress distribution of friction welding joint of 2205 duplex stainless steel[J].Heat Treatment of Metals,2016,41(12):38-41(in Chinese).
[8] 蒋文春,Woo Wanchuck,王炳英,等. 中子衍射和有限元法研究不锈钢复合板补焊残余应力[J]. 金属学报,2012(12):1525-1529.Jiang Wenchun,Woo Wanchuck,Wang Bingying,et al. A study of residual stress in the repair weld of stainless steel clad plate by neutron diffraction measurement and finite element method[J].Acta Metallurgica Sinica,2012(12):1525-1529(in Chinese).
[9] 税正伟. 焊后热处理对 L245NCS微合金钢焊接残余应力的影响[J]. 金属热处理,2012,37(7):35-37.Shui Zhengwei. Effect of postweld heat treatment on welding residual stress of L245NCS microalloy steel[J].Heat Treatment of Metals,2012,37(7):35-37(in Chinese).
[10] Olson M D,Hill M R,Clausen B,et al. Residual stress measurements in dissimilar weld metal[J].Experimental Mechanics,2015,55(6):1093-1103.
[11] Liu C,Dong C L. Internal residual stress measurement on linear friction welding of titanium alloy plates with contour method[J].Transactions of Nonferrous Metals Society of China,2014,24(5):1387-1392.
[12] Nervi S,Szabó B A. On the estimation of residual stresses by the crack compliance method[J].Computer Methods in Applied Mechanics and Engineering,2007,196(37/38/39/40):3577-3584.
[13] 徐小严,吕玉廷,张 荻,等. 中子衍射测量残余应力研究进展[J]. 材料导报,2015(9):117-122.Xu Xiaoyan,Lü Yuting,Zhang Di,et al. Measuring residual stress by neutron diffraction[J].Materials Review,2015(9):117-122(in Chinese).
[14] Schajer G S,Ruud C O.Practical Residual Stress Measurement Methods[M]. Chichester:Wiley,2013.
[15] Schajer G S,Prime M B. Use of inverse solutions for residual stress measurements[J].Journal of Engineering Materials and Technology,2006,128(3):375-382.
[16] Pachpatte B G.Multidimensional Integral Equations and Inequalities[M]. Paris:Atlantis Press,2011.
[17] Farrahi G H,Faghidian S A,Smith D J. An inverse method for reconstruction of the residual stress field in welded plates[J].Journal of Pressure Vessel Technology,2010,132(6):61205.
[18] 王仁宏. 数值逼近[M]. 北京:高等教育出版社,2012.Wang Renhong.Numerical Approximation[M]. Beijing:Higher Education Press,2012(in Chinese).
[19] 王振杰. 测量中不适定问题的正则化解法[M]. 北京:科学出版社,2006.Wang Zhenjie.Regularized Methods for Ill-Posed Problems in the Measurement[M]. Beijing:Science Press,2006(in Chinese).
[20] 唐志涛. 航空铝合金残余应力及切削加工变形研究[D]. 济南:山东大学机械工程学院,2008.Tang Zhitao. Residual Stresses and Deformations of Aerospace Aluminum Alloy in Machining[D]. Jinan:School of Mechanical Engineering,Shandong University,2008(in Chinese).
