深水钻井送入管柱的载荷计算与强度分析
2018-05-18管志川李敬皎赵效锋腾学清孙宝江
管志川, 李敬皎, 韩 超, 张 波, 赵效锋, 腾学清, 孙宝江
(1.中国石油大学石油工程学院,山东青岛 266580; 2.中国石油塔里木油田分公司油气工程研究院,新疆库尔勒 841000)
送入管柱是深水钻井中非常重要的管柱结构之一,主要功能是将大尺寸、高重量的表层导管和套管柱送入海底泥线以下[1-2]。在海底浅部地层导管段和表层套管段的深水钻井过程中,由于没有隔水管的保护,在海洋环境载荷、钻井船偏移运动以及被送入的底部套管柱重力等联合作用下,送入管柱的受力和变形会发生复杂变化。如果送入管柱的载荷计算不准和强度设计不合理,将会给深水钻井作业带来安全隐患,墨西哥湾和巴西海域钻井中都发生过因送入管柱失效而导致的巨大经济和环境损失[3-4]。目前,关于送入管柱的受力与强度设计主要以静态分析为主。Azar等[5]提出了准静态环境载荷的概念;Sathuvalli等[6]和Paslay等[7]针对卡瓦挤毁问题进行了相关的试验研究,提出了基于R-S模型的卡瓦挤毁载荷计算新方法;畅元江等[8]提出了搜索波浪最大相位角的最大Mises应力准则,分析了波流联合作用下隔水管的准静态性能;张辉等[9]建立了导管喷射安装过程中的管柱静力学模型,用于指导导管喷射安装作业;Plessisg等[10]提出了一种用于深水钻井的超大承载能力的送入管柱系统,并介绍了一系列相关支撑技术。笔者综合考虑海洋环境载荷、钻井船偏移运动以及底部套管柱重力等因素的影响,基于材料力学和Euler-Bernoulli梁理论,建立无隔水管环境下送入管柱的准静态载荷计算模型,并结合工程实例分析不同因素对送入管柱受力、变形和强度安全的影响,为深水钻井送入管柱的载荷计算和强度设计提供理论依据。
1 载荷计算模型建立与求解
在海底浅部地层导管段和表层套管段的深水钻井过程中,送入管柱裸露于海水之中,其上端与钻井船或钻井平台连接,下端连接喷射钻具组合、表层导管和套管柱,在作业过程中受重力、浮力、波浪力、海流力、套管柱摩擦力和管柱内外压力等载荷的作用发生变形,如图1所示。随着水深的加深,裸露在海水中的送入管柱受力环境更加复杂,为建立送入管柱载荷计算的数学模型,假设[11-12]:①忽略钻柱接头的影响,送入管柱系统为均质、各向同性、线弹性的钢质圆管;②送入管柱视为横向受载的纵横弯曲梁。由于送入管柱的长度远大于直径,且挠度相比其长度很小,符合小变形假设理论;送入管柱全部沉浸在海水中,不考虑钻井船的升沉运动和送入管柱在垂向上的位置变化;海流、波浪和送入管柱变形处于同一个二维平面内,波流载荷方向相同,忽略海流的升力作用。
基于以上假设,取变形后送入管柱的一个微元体dx进行分析,纵坐标x与重力方向相反,横坐标y反映送入管柱的挠度,如图2所示。根据Euler-Bernoulli弯曲梁理论得到送入管柱的变形控制方程,即

(1)
式中,E为弹性模量,Pa;I为截面惯性矩,m4;T(x)为位置x处管柱横截面受到的有效轴向载荷,N;W为单位长度送入管柱在海水中的重力,N;F(x)为位置为x处单位长度送入管柱受到的波流载荷,N。
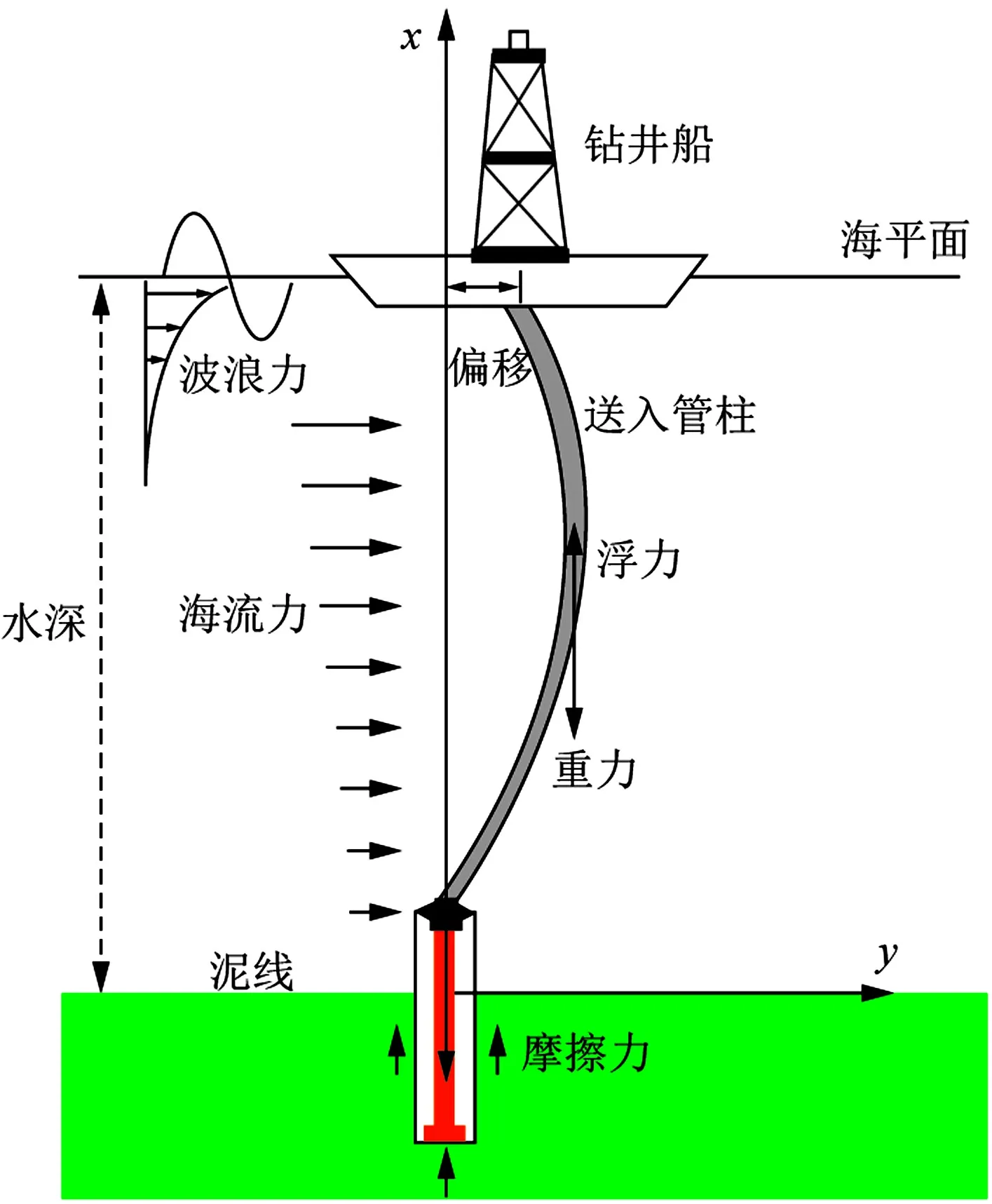
图1 深水钻井送入管柱系统物理模型Fig.1 Physical model of deepwater landing string system
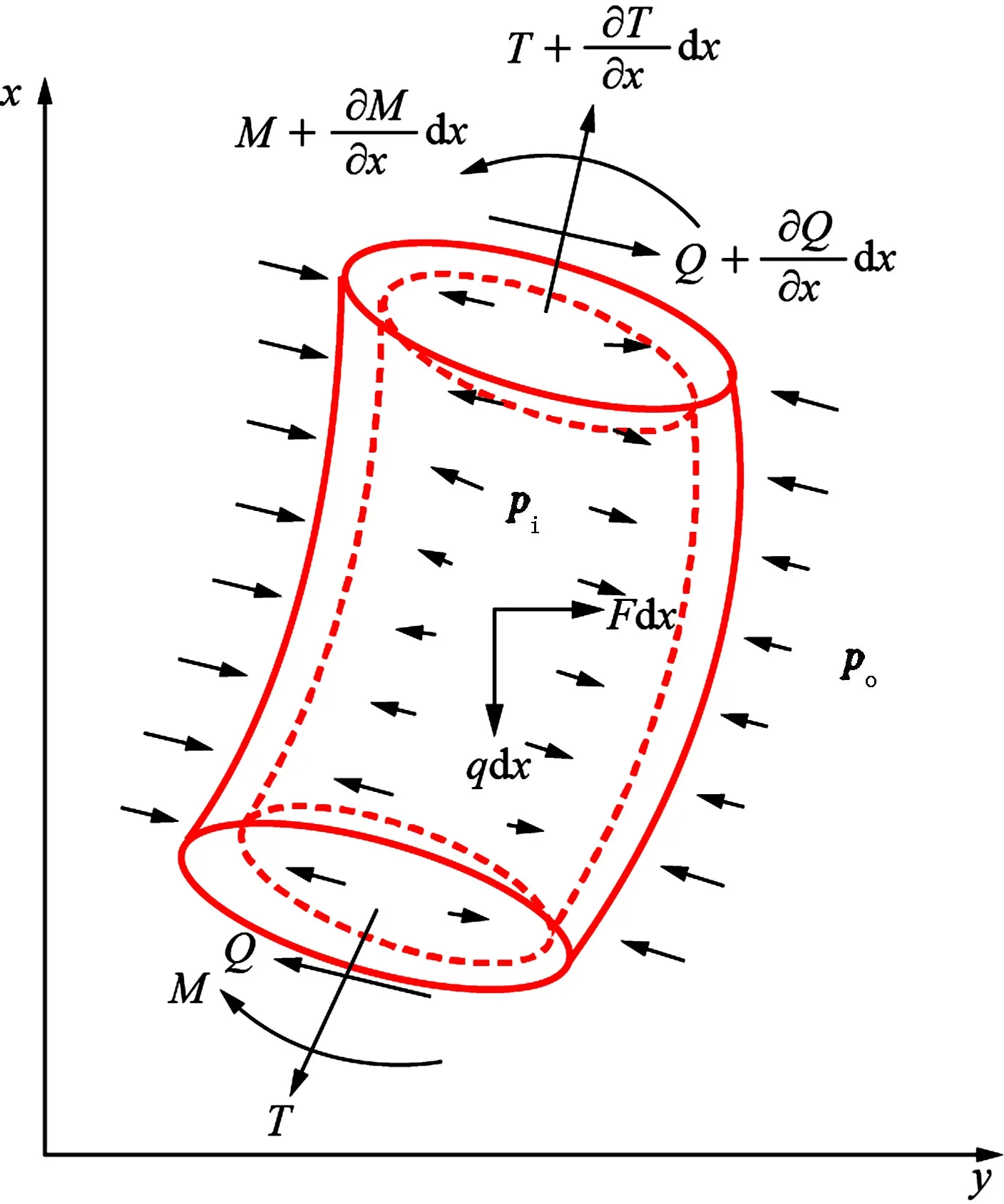
图2 送入管柱微元体受力分析示意图Fig.2 Force analysis diagram of landing string infinitesimal segment
1.1 送入管柱的有效轴向载荷
送入管柱在作业过程中处于整体受拉的状态,在某截面处所承受的有效轴向载荷为
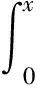
(2)
其中
式中,T0为送入管柱底部所受的拉伸载荷,N;T1为单位长度管柱所受内外静液柱压差产生的虚拉力,N;D和d分别为送入管柱外径和内径,m;ρs、ρm和ρw分别为送入管柱、钻井液和海水的密度,kg/m3。
1.2 波流载荷
波流载荷主要包括海流载荷和波浪载荷,波流共同作用时,采用修正的Morison方程计算联合作用力。在波流场中,水质点的横向运动等于波浪引起的运动与海流引起的运动的迭加,考虑由波浪运动引起的水质点速度达到最大值,且其方向与海流速度方向一致时的情况,此时作用于单位长度送入管柱上的波流载荷为

(3)
式中,CD为海水拖拽力系数;u为海流的水平速度,m/s;v为波浪水质点的水平速度,m/s;CM为海水惯性力系数。
海流速度缓慢,可视为恒流,作用于单位长度送入管柱的海流力fc也就是管柱对海流的阻力。在无实测资料的情况下,采用挪威船级社推荐的仅考虑潮流和风漂流的合成流速沿垂向高度的分布变化计算公式[13],即

(4)
其中
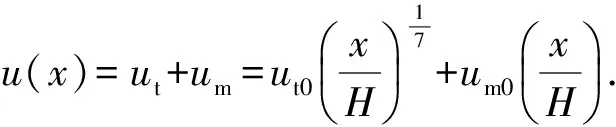
式中,ut和um分别为潮流流速和风漂流流速,m/s;ut0和um0分别为潮流表面流速和风漂流表面流速,m/s;H为水深,m。
波浪载荷是由波浪水质点与送入管柱间的相对运动所引起的。由于管柱是小直径构件,直径波长比远小于0.2,因此采用Morison方程和Stokes五阶波浪理论,计算作用在单位长度送入管柱的波浪载荷,即

(5)
采用Airy线性微幅波理论[13]计算波浪水质点的水平速度和加速度,即
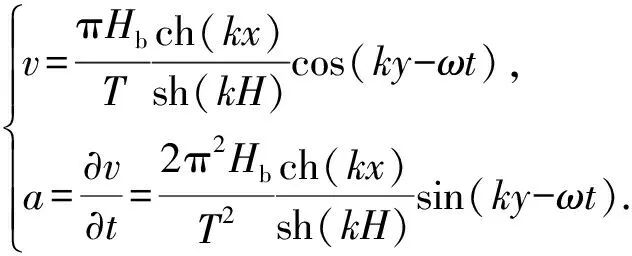
(6)
式中,a为波浪水质点的水平加速度,m/s2;Hb为波高,m;T为波浪周期,s;k为2π长度内的波数;ω为表面波角频率;t为波浪作用时刻,s;ky-ωt为表面波相位角。
1.3 模型求解
采用加权余量法对送入管柱变形控制方程求解[14],步骤如下:
(1)自下而上将送入管柱均分为n等份,管柱底节点和顶节点分别设为1和n,每个单元长度为l,设单元试函数为
yi=Ci,1+Ci,2x+Ci,3x2+Ci,4x3+Ci,5x4,x∈[0,l],
i=1,2,…,n.
(7)
(2)应用配点法,将单元试函数带入变形控制方程,得到内部余量方程Ri(x),使其在定义域中的l/2处的余量为0,即
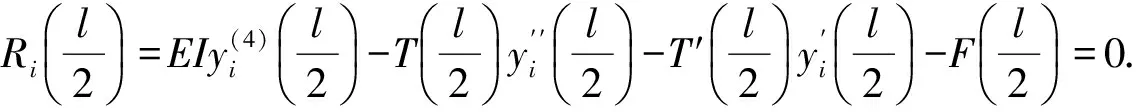
(8)
(3)为保证各单元在几何和物理性质上的连续性,相邻两个单元之间须满足挠度y、转角θ、弯矩M和剪力Q的连续条件,即
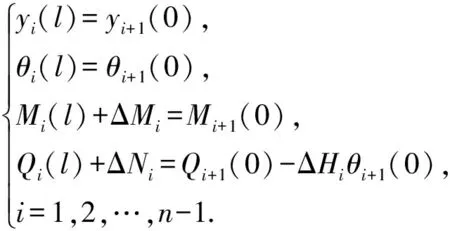
(9)
由于送入管柱顶部与顶驱相连,钻井船相对海底井口发生偏移,上端边界视为固支,yn(l)=y0,θn(l)=0。根据不同作业工况,管柱下端边界条件可分为:送入管柱入泥前下端为自由端,M1(0)=0,Q1(0)=0;当导管入泥深度小,忽略地层对其横向约束的作用,将管柱下端边界视为绞支,y1(0)=0,M1(0)=0;当导管入泥较深时,地层可承受导管横向变形产生的应力载荷,此时将管柱下端边界视为垂向上可自由运动的滑支,y1(0)=0,θ1(0)=0。文中无特殊说明时,下端边界均视为滑支。
(4)将单元试函数带入送入管柱的内部余量方程、连续性条件及边界条件等关系式中,可得到模型的求解方程组。编程计算求得各单元试函数的待定系数Cij(i=1,2,…,n;j=1,2,3,4,5),进而求出送入管柱任意位置处的横向位移、转角、弯矩及剪力等参数。单元n取值足够小时,可以得到较高精确的计算结果。
2 送入管柱强度分析
考虑送入管柱在海水中承受轴向力、外挤力、内压力和横向载荷的共同作用,其中送入管柱凸侧所承受的轴向复合应力为有效轴向力和横向变形产生的弯曲正应力的矢量和[15]。由于弯曲正应力与计算点到中性轴的距离有关,因此在同一截面上的最大值位于外边缘处。根据厚壁圆筒理论及拉梅公式[16],得到管柱内应力分布为
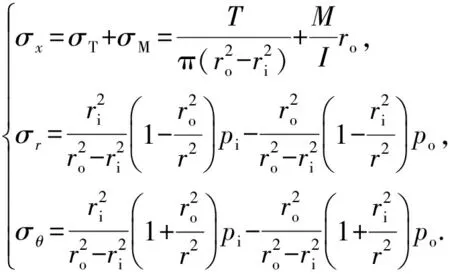
(10)
式中,σx、σr和σθ分别为轴向复合应力、径向应力和周向应力,MPa。ro和ri分别为送入管柱外半径和内半径,m;po和pi分别为管外海水与管内钻井液的静液柱压力,MPa。
对送入管柱进行抗拉强度分析时,考虑到管柱横向变形产生的弯曲正应力的影响,应使用轴向复合应力进行校核,即
σxSt≤[σa].
(11)
式中,[σa]为管柱材料的许用拉伸强度(一般取材料最小屈服强度的90%),MPa。
对送入管柱进行屈服强度分析时,应用Von Mises等效应力及形状改变必能理论的失效准则(API RP 16Q)[16],即
St≤[σs].
(12)
式中,[σs]为管柱材料的最小屈服强度,MPa。
3 实例计算
3.1 基本参数
以某口深水井为例,该井作业水深为1 500 m,送入管柱外径为149.2 mm(壁厚15.25 mm),弹性模量为210 GPa,泊松比为0.3,海水密度为1 025 kg/m3,钻井液密度为1 200 kg/m3,管柱材料密度为7 850 kg/m3,风流表面流速为0.5 m/s,潮流表面流速为0.3 m/s,海水拖拽力系数为0.8,惯性力系数为2.0,波浪周期为8 s,波浪高为5 m。为定量对比研究海洋环境载荷对送入管柱力学行为的影响,选用6种波流剖面组合作为环境参数,如表1所示。影响因素分析时,无特殊说明均选用类型二中的潮流和风流的表面流速及波高。
送入管柱底部所承受的拉伸载荷是由底盘、导管送入工具、喷射导管及表层套管等重力产生的,为便于因素分析,定义无量纲参数k为底部套管柱重力与送入管柱总浮重(包含内部钻井液等重量)之比。

表1 6种不同的波流剖面组合Table 1 Six different combinations of wave and current profile
3.2 海洋环境载荷的影响
图3为不同波流剖面时波流载荷沿水深的变化曲线。距离海底前1 450 m时,波流载荷和海流载荷均随水深的减小呈线性增加,二者斜率几乎相同;距离海面约50 m时,波流载荷突然增大,剖面类型一、二、三的最大值分别为371、467和574 N/m。由于波浪载荷作用深度有限,只在海面以下约50 m的范围内对送入管柱力学特性产生影响,且在海面处载荷达到最大值。在分析送入管柱顶部的力学特性时须考虑波浪载荷产生的作用力。
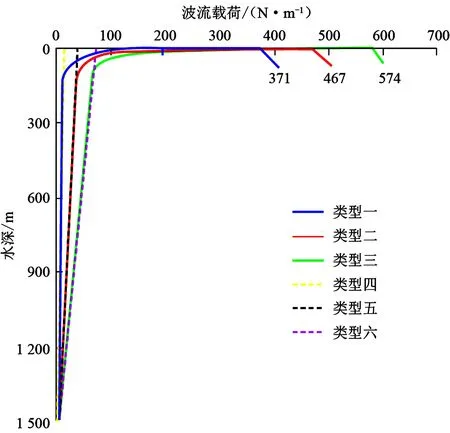
图3 波流剖面对波流载荷的影响Fig.3 Effects of wave and current profile on sealoads
在k为0.9、钻井船偏移量为0的情况下,6种剖面对送入管柱横向变形和顶部弯矩的影响如图4所示。从图4中看出,在同一海流速度下,送入管柱的变形随水深的增加先增大后减小,在中间部位达到最大值,数值分别为1.4、5.2和11.7 m;随着海流速度的增加,管柱横向变形整体增加,但考虑波浪载荷后发现其对管柱横向变形几乎没有影响。海流速度越大,管柱顶部弯矩越大;同一海流速度下,由于波浪载荷的影响,管柱顶部弯矩增加约6 kN·m,这表明波浪载荷对送入管柱顶部弯矩有较大影响,而对其中下部力学性能的影响很小。

图4 波流剖面对送入管柱横向变形和顶部弯矩的影响Fig.4 Effects of wave and current profile on lateral deformation and top bending moment of landing string
3.3 底部套管柱重力的影响
送入管柱在作业过程中,被送入的底部套管柱重力对管柱力学特性有较大影响。不同k值时送入管柱横向变形随水深的变化曲线如图5所示。由图5可知,随着底部套管柱重力的增加,送入管柱横向变形逐渐减小。当k为0.3和1.8时,最大变形分别为9.3和3.2 m,可见送入管柱的横向变形对底部套管柱重力的变化非常敏感。

图5 不同k值时送入管柱的横向变形Fig.5 Effects of different k value on lateral deformation of landing string
图6为钻井船偏移量为0时送入管柱顶部弯矩和底部弯矩的变化曲线。从图6中看出,随着k值增大,弯矩逐渐减小,且顶部弯矩始终大于底部弯矩,因此强度校核时要着重考虑管柱顶部承受弯矩的能力。当k为0.3和1.8时,顶部弯矩分别为42.9和21.3 kN·m。这表明底部套管柱重力影响送入管柱的力学性能,是送入管柱强度设计须考虑的关键因素。

图6 不同k值时送入管柱的弯矩变化Fig.6 Effects of different k value on bending moment of landing string
3.4 钻井船偏移运动的影响
图7为k为0.9时送入管柱横向变形和顶部弯矩随钻井船偏移量的变化曲线。随着钻井船偏移量的正向增加,送入管柱横向变形增大,但增加的幅度减小。随着偏移量的负向减少和正向增加,顶部弯矩先减小后增大,但由于底部套管柱重力的影响,造成弯矩达到最小值时所对应的偏移量不同。由此可见,钻井船偏移量对送入管柱横向变形和顶部弯矩影响显著,控制合适的偏移量可以有效地减小管柱顶部弯矩。

图7 送入管柱横向变形和顶部弯矩随钻井船偏移量的变化Fig.7 Variation of lateral deformation and top bending moment under different k value with vessel offset
在喷射下导管阶段,导管下端触达海底时的倾角是安装作业成功的关键,此时送入管柱的下边界视为绞支。图8为不同k值时导管下端倾角随钻井船偏移量的变化曲线。从图8中看到,随着偏移量的负向减小和正向增加,导管下端倾角先减小后增加,倾角为0°时所对应的偏移量不同,且当钻井船相对井口有相同的偏移量时,正向偏移比反向偏移所引起的倾角更大,保持偏移量在-20~-8 m时导管安装的垂直性最好。因此根据实际工况,及时合理的调整钻井偏移量对导管喷射安装及送入管柱作业安全至关重要。
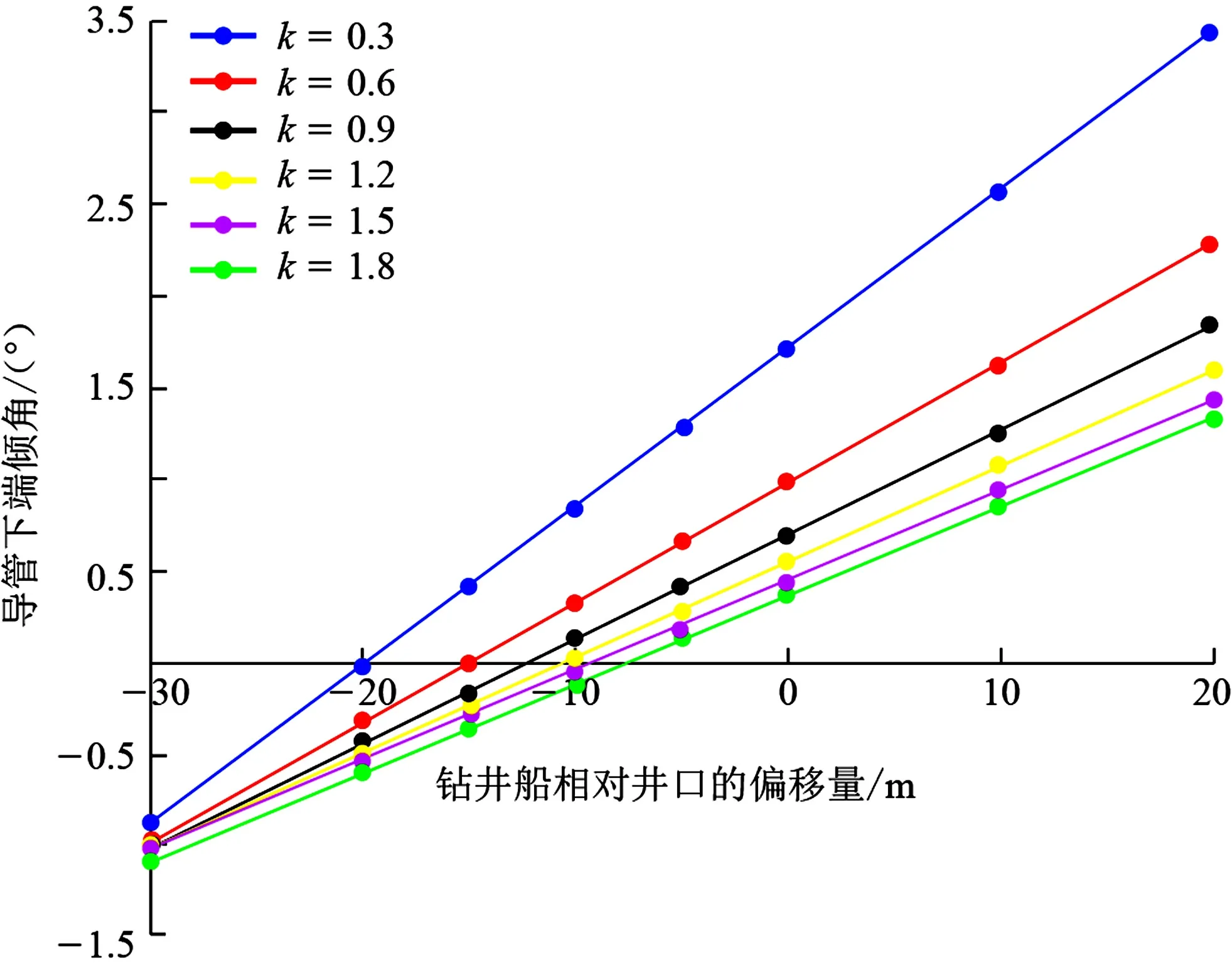
图8 导管下端倾角随钻井船偏移量的变化Fig.8 Variation of dig angle of conductor under different k value with vessel offset
3.5 送入管柱强度分析
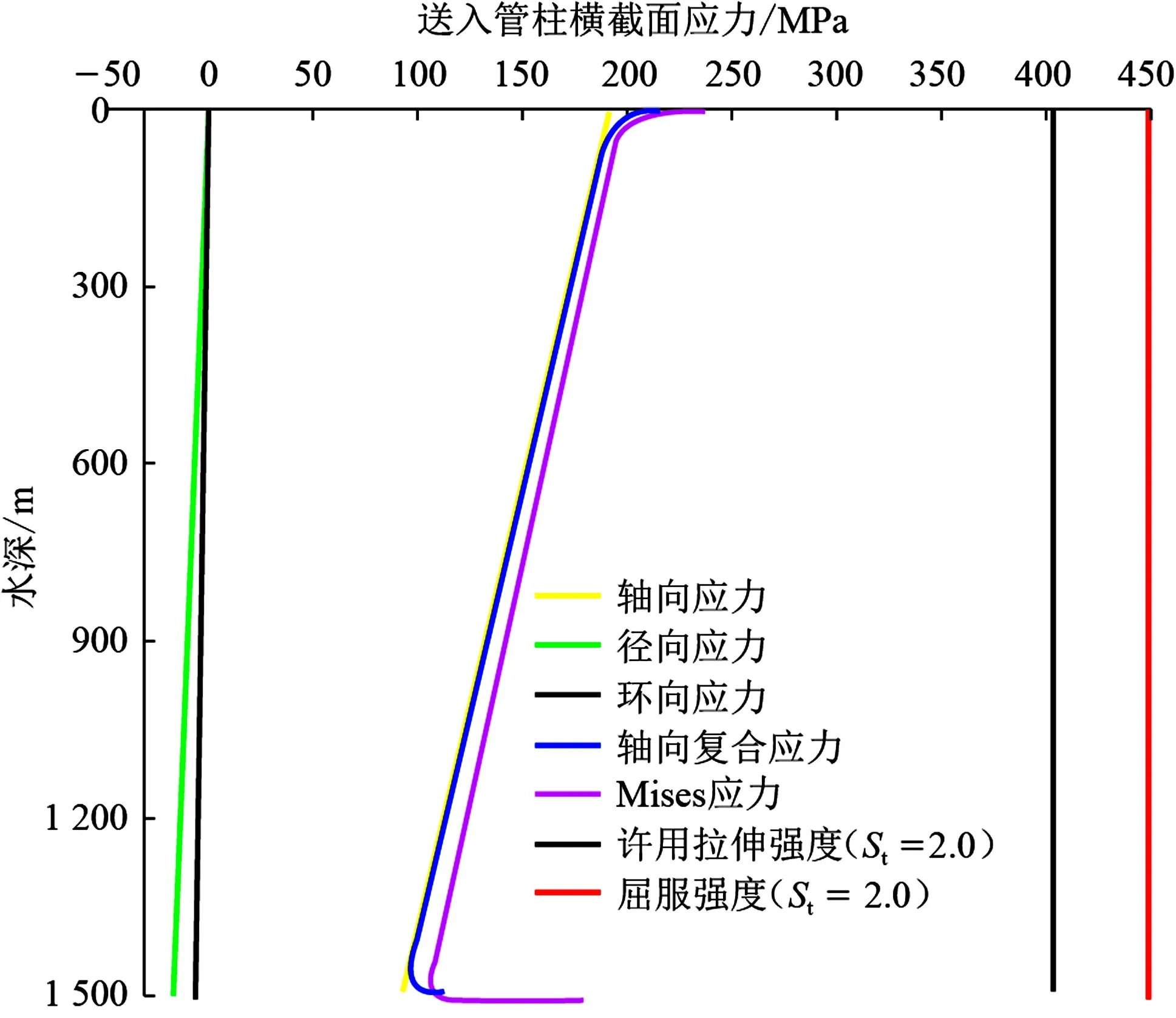
图9 送入管柱横截面应力分布Fig.9 Stress distribution of landing string cross section
图9为k为0.9、钻井船偏移量为0时送入管柱横截面应力分布。选取深水钻井常用的安全系数为2.0的S135钻杆进行强度校核分析,由图9可知,送入管柱整个截面均满足强度要求。由于径向应力和环向应力很小,为便于计算,可基于轴向复合应力和许用拉伸强度对送入管柱进行强度设计。管柱横向变形产生的弯曲正应力使得Mises应力在管柱顶部和底部出现突增,其中确定管柱顶部截面为危险截面。因此在管柱顶部选用大壁厚、高强度的钻杆可以更大限度地满足其强度要求。
不同k值时送入管柱顶部Mises应力随钻井船偏移量的变化如图10所示。管柱顶部Mises应力与钻井船偏移量呈线性关系,当钻井船正向偏移26.8、22.9和20.1 m时,3种工况下送入管柱顶部的弯矩和弯曲正应力均为0,此时Mises应力取得最小值。当底部套管柱重力减小时,管柱顶部Mises应力减小,钻井船安全偏移范围增大,在一定程度上保证了送入管柱施工作业的安全性。

图10 管柱顶部Mises应力随钻井船偏移量的变化Fig.10 Variation of top Mises stress of landing string with vessel offset
4 结 论
(1)综合考虑海洋环境载荷、钻井船偏移运动和底部套管柱重力等因素的影响,基于Euler-Bernoulli梁理论建立了无隔水管环境下送入管柱的准静态载荷计算模型,应用加权余量法进行求解,定量分析了送入管柱的横向变形、弯矩、导管下端倾角及应力水平的变化规律。
(2)随着海流载荷的增大,送入管柱的横向变形和顶部弯矩均增大,而波浪载荷仅对送入管柱顶部弯矩有较大影响;底部套管柱重力对管柱力学性能有明显影响,是送入管柱强度设计须考虑的关键因素;钻井船偏移量对送入管柱顶部弯矩和导管下端倾角有很大影响,在不同工况下保持合适的偏移量有助于送入管柱安全高效的作业。
(3)由于送入管柱的径向应力和轴向应力很小,且管柱横向变形产生的弯曲正应力造成Mises应力在管柱顶部和底部出现突增,因此可基于轴向复合应力进行送入管柱的强度设计。在管柱顶部和底部选用大壁厚、高强度的钻杆,进一步增加深水钻井送入管柱的强度安全。
参考文献:
[1] BORDET L, FRANCHI J, GRANGER S, et al. Innovative forging process allows safer and cost effective heavy duty landing string for deepwater applications[R]. SPE 180289, 2016.
[2] API Recommended Practice 7G. Recommended practice for drill stem design and operating limits[S]. Washington D C: American Petroleum Institute, 1998.
[3] BREIHAN J W, ALTERMANN J A, JELLISON M J. Landing tubulars design, manufacture, inspection and use issues[R]. SPE 67723, 2001.
[4] 周俊昌,付英军,朱荣东.深水钻井送入管柱技术及其发展趋势[J].石油钻探技术,2014,42(6):1-7.
ZHOU Junchang, FU Yingjun, ZHU Rongdong. Design method and development trend of landing strings in deepwaterdrilling[J]. Petroleum Drilling Techniques, 2014,42(6):1-7.
[5] AZAR J J, SOLTVEITOL R E. A comprehensive study of marine drilling risers[R]. SPE 7200, 1978.
[6] SATHUVALLI U B, PAYNE M L,SURYANARAYANA P V, et al.Advanced slip-crushing considerations for deepwater drilling[J]. SPE Drilling & Completion, 2002,17(17):210-223.
[7] PASLAY P R, PATTILLO P D,PATTILLO Ⅱ P D, et al. A re-examination of drillpipe/slip mechanics[R]. SPE 99074, 2006.
[8] 畅元江,陈国明,孙友义,等.深水钻井隔水管的准静态非线性分析[J].中国石油大学学报(自然科学版),2008,32(3):114-118.
CHANG Yuanjiang, CHEN Guoming, SUN Youyi, et al. Quasi-static nonlinear analysis of deepwater drilling risers[J]. Journal of China University of Petroleum(Edition of Natural Science), 2008,32(3):114-118.
[9] 张辉,高德利,唐海雄,等.深水导管喷射安装过程中管柱力学分析[J].石油学报,2010,31(3):516-520.
ZHANG Hui, GAO Deli, TANG Haixiong, et al. Tubular mechanics in jetting operation of conductor under deepwater condition[J].Acta Petrolei Sinica, 2010,31(3):516-520.
[10] PLESSISG J, RICHARD V, SVEIN-INGE R, et al. Landing string: breaking the 2.5 million pounds limit[R]. SPE 178777, 2016.
[11] 李朝玮,樊洪海,汪志明,等.非均匀海流、表面波与内孤立波共同作用下钻井隔水管准静态分析[J].中国海上油气,2015,27(2):78-86.
LI Zhaowei, FAN Honghai, WANG Zhiming, et al. Quasi-static analysis of a drilling riser under combined loads of non-uniform currents, surface waves and internal solitary waves[J]. China Offshore Oil and Gas, 2015,27(2):78-86.
[12] 林秀娟,肖文生,王鸿雁.深水采油树下放过程钻柱力学分析[J].中国石油大学学报(自然科学版),2011,35(5):125-129.
LIN Xiujuan, XIAO Wensheng, WANG Hongyan. Drill string mechanical analysis of running deepwater oil tree[J]. Journal of China University of Petroleum(Edition of Natural Science), 2011,35(5):125-129.
[13] FAlTINSEN O M.船舶与海洋工程环境载荷[M].杨建民,译.上海:上海交通大学出版社,2008.
[14] 徐次达.固体力学加权残值法[M].上海:同济大学出版社,1987.
[15] BRADFORD D W, PAYNE M L, SCHULTZ D E, et al. Defining the limits of tubular-handling equipment at extreme tension loadings[J]. SPE Drilling & Completion, 2009, 24(1):72-88.
[16] 杨海波,曹建国,李洪波. 弹性与塑性力学简明教程[M]. 北京:清华大学出版社, 2011.
