《机器学习》课程教学案例
——手写数字识别系统开发
2018-05-18米吉提阿不里米提吾米提尤努斯艾斯卡尔艾木都拉
米吉提·阿不里米提,吾米提·尤努斯,艾斯卡尔·艾木都拉
(新疆大学信息科学与工程学院,乌鲁木齐 830046)
0 引言
人工智能、机器人、大数据等已经离不开我们的生活。教育部发文,机器人与编程被列入2018高中必修课。机器人素质教育进入校园,其核心概念是机器学习。机器学习在诸多领域成功的应用与发展,己成为信息处理领域的基础和热点[1-2]。机器学习的相关的课程从研究生教育逐渐进入高中教育阶段。作为一门实践性极强的课程,其内容自然联系到诸多抽象概念和基础课程。虽然,机器学习相关的教学课程及网上课堂很多[3],内容也丰富多样,但缺乏简单易懂的案例教学。将复杂的内容有效教授给学生、以及让学生掌握其精粹、理解其内涵是件艰巨的任务。通过案例场景引出相关概念、技术,以此为主线增强学生的学习信心可能是机器学习课程最有效的教学方法。一个具体案例能有效掌握主题、消除疑惑、理解抽象概念等方面取到举一反三的目标[4]。
从多年的教学工作当中发现,大部分教材及参考书,注重抽象概念及普遍理论的讲解。对于具体简单的例子的讲解案例严重缺乏。导致学习过程只是现成工具的套用,最终对抽象概念一知半解,越学越觉得吃力、脱离实践、死记硬背。学习效率差,直接导致厌学。甚至有的学生直接提出“既然有很好的现成工具就不需要学习,直接应用即可”。
机器学习方法之多,如 HMM、GMM、K-means、SVM、DNN等,内容之抽象,很容易导致理论脱离实践。本文采用比较直观的例子“手写数字的识别”作为例子讲解一个以线性分类器为核心的机器学习方法。多维线性函数是SVM、DNN等效果比较好的机器学方法的基础,直观并易于理解、容易实现。对于初学者是个理想的实践过程。
1 模型的建立
机器学习的目标可以是各种信息,包括视觉信号及听觉信号等。比较典型的是语音及文字信息。其中文字图像比较直观,用于机器学习教学效果更好。但是手写数字包含随机变化成分,因为我们知道每个人书写方式、习惯、大小、角度等不会完全一样,相同的数字一个人写两次也不会完全一样。但是每个文字或数字都有固定的模版。我们可以用模版的匹配度量来区分不同数字或进行分类。因此,即需要很好的机器学习模型,有需要大量样本的训练过程。
可以用较复杂的概率统计概念来设计一个模型[3],也可以用简单的线性函数来实现分类过程。机器学习模型需要在训练样本中训练。类似于,一个小孩开始学习认知数字。先让孩子学习各个数字,然后让其辨认一些数字。刚开始,孩子虽然能正确辨认出比较规整的手写数字,也会误判一些写的较潦草的数字。慢慢通过学习(学习各种手写样本)就能不断提高准确率。
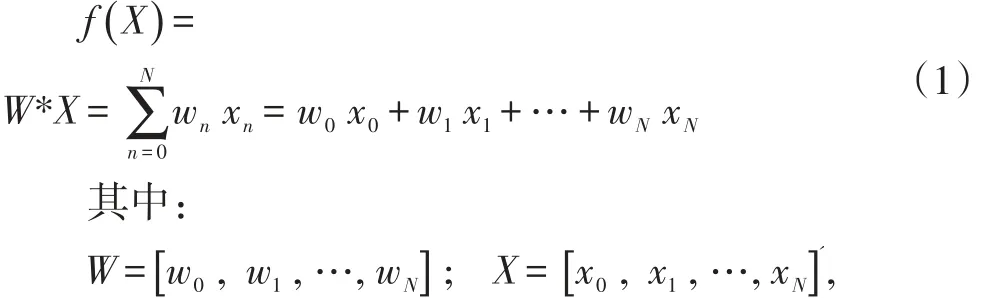
机器学习过程需要模型和样本两部分,首先设计一个数学模型,其次在大量样本上学习后调整模型的参数,并用该模型去判断新的手写数字。公式(1)一个线性模型,是另外两个重要机器学习模型的基础,深度神经网络(DNN)和支持向量机(SVM)。
设x0=1

公式(2)计算结果是对某个样本数字的特征向量X的预测值。机器学习的目的是提高该预测的正确率。这里要训练的模型参数是W=[ ]w0,w1,…,wN。

图1 单个线性分类器模型
输入一系列样本数据X(1),X(2),X(3),…我们的训练目标是找到合适的参数W使得若(2)大于零则正确,小于零则错误。这是一个简单的2类分类技术,即只能用于一个数字的辨认。
训练过程是一个循序渐进过程。先W给指定一个初始值,然后根据对样本的识别结果进行调整。若有10个训练样本X(1),X(2),X(3),…,X(10)对应于0到9十个数字。模型的训练目标是[…y(k)…] =[-1,…,-1,1,-1..],对应数字“3”时y(k)=1,其他都等于-1。假设,我们通过公式(2)计算出来的结果是“全部大于零”,则错误率是90%,若“全部小于零”,则错误率是10%。因为我们的目标是正确识别数字“3”。只有测试“3”时f(X)结果大于零,其他样本时小于零才是正确的结果。即,正确识别结果应该是sign(f(X))=[-1,-1,-1,1,-1,…,-1]。
循序渐进的方法是先设置多次循环,每次循环给所有参数[w0,w1,…,wN]进行调整,最终获得最佳参数W。每次对参数的微调方式是公式(3)
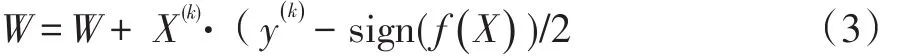
其中,(y(k)-sign(f()X)决定调整的方向。若预测值和实际值相同则没必要调整,否则向y(k)的方向进行调整。X(k)是调整的幅度,是线性函数的偏微分。

虽然该例子很简单,但是任何复杂的机器学习模型都是通过对公式(1)~(3)的改变或优化获得的,机器学习的核心思路没变。若将公式(2)换成公式(4),模型就变成了标准的感知器(perceptron)模型。图1显示的是一个数据(如:数据“3”)的预测模型,10个这样的模型并联成起来就成了识别10个数据的单层原始神经网络模型。

2 试验数据准备
图像在计算机中的简单(单色)表示方法是矩阵形式,如图2。这些信号输入机器学习模型时,需要转换成一系列特征向量。特征向量可能是一维的,也可能是二维的。相应的特征数据有有统计特征、钜、方向特征等等,也可能是图像矩阵本身。
在监督机制建设中要重点强化企业的成本监督和相关管理工作,要以成本作为监督的目标,理顺企业生产、管理的经济关系,从成本控制的角度构建起有针对性、可执行的监督平台和监督制度,真正将监督工作的重点放在对企业各项成本的控制工作上,提升企业成本管理、运营管理的效率,打造企业在生产、管理和经营上的经济、组织与成本优势。
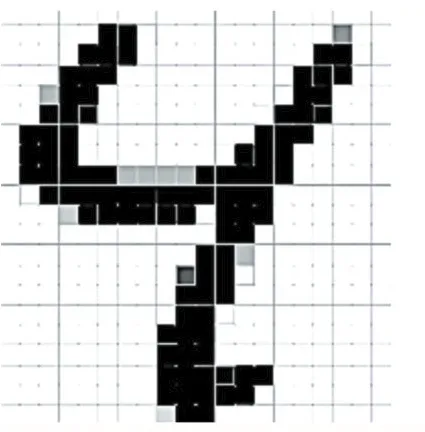
图2 手写数字矩阵实例
数据准备过程需要图像的采集、二值化、规范化、细化等过程。最终获得大小规整的数字矩阵。图2显示一个数字矩阵,白色用0表示,黑色用1表示,就能获得2维矩阵。
大家可以自己找几个人进行手写数字的采样和预处理过程。也可以直接用免费数据MNIST[5],MNIST提供了6万个训练样本,和1万个测试样本,每个样本是一个28×28矩阵。收集样本时要注意,训练样本和测试样本是不同人提供的。
由于我们用的线性模型是一维向量模型,所以需要对二维向量进行降维、或直接将矩阵逐行拼接成一维向量。所有样本X(1),X(2),X(3),…,X(N)和对应的正确数字标注[y(1),y(2),y(3),…,y(N)]交给模型。X(i)是个一定长度(28×28)的向量,y(i)是对应的标注信息,-1或 1,例如模型的目的是识别数字“3”则对应“3”的标注是1,其他都是-1。训练结束后,在独立的测试样本上进行测试并获得试验结果。
3 实现过程
模型实现方法比较简单,大家可以用任何编程语言,如:Python,C,MATLAB等,实现。如下我们提供的伪代码。其中X是所有训练数据,每行是一个样本,总行数M是总样本数,列数是一维特征向量,长度为N,注意x0=1,即将矩阵X的第一列全设置成1,对应的参数w0成为偏移量。实际信号的特征值长度是N-1。Function Linear_model(X,Y) {
[M,N]=size(X) #获得样本数M,和向量长度N
W=ones(N) #参数初始化成全1的向量
err=0 #错误率,初始化
while(err>0.1) #err是错误率。或者可以循环100次
{
for i=1:M #循环计算每个样本的预测值,并对参数更新
{
Fx=sign(W*X[i,:]) # 注意矢量相乘,X[i,:]需要转值
W=W+X[i,:]·(Y[i]-Fx)# 更新参数
err=err+(Y[i]-Fx)/2 #错误累加
}
err=err/M #错误率
}
return W }
我们取了20个人的200个样本数据进行训练,并在少量测试数据上进行测试,错误率为22%。这只是一个数字的识别过程,要实现10个手写数字的识别模型,简单的并联即可。
4 结语
《机器学习》作为一门实践性极强的课程,其内容自然和诸多抽象概念和基础课程有关。将这些内容有效教授给学生,以及让学生掌握其精粹、理解其内涵是件艰巨的任务。本文以教学为目的介绍了一个简单且典型的机器学习模型机器设计和训练过程。虽然关于机器学习的书籍及参考资料很多,对于初学者的简单案例教学形式的材料严重缺乏。因此,尽量用通俗易懂的方式讲解了机器学习完整过程,避免了概念的抽象化,注重具体细节和实现过程。难免有不足之处,希望大家批评指正。
参考文献:
[1]余明华,冯翔,祝智庭.人工智能视域下机器学习的教育应用与创新探索.远程教育杂志,2017-05-20.
[2]邓志鸿,谢昆青.机器学习课程的教学实践——以北京大学“智能科学与技术”本科专业为例.计算机教育,2016-10-10.
[3]Christopher Bishop.“Pattern Recognition and Machine Learning”.Springer press,2007.
[4]李勇.本科机器学习课程教改实践与探索.计算机教育,2015-07-10.
[5]http://yann.lecun.com/exdb/mnist/.
