基于模糊和解耦的超临界机组协调控制研究

董子健， 毛求福

(华北电力大学 控制与计算机工程学院，河北 保定 071003)

0 引言

随着我国电力行业的迅猛发展，火力发电机组承担着主要用电量供应任务，如何保证火电机组稳定、安全高效的运行一直是电力行业研究的重点。由于超临界发电技术比较成熟，并且具有热效率高、可靠性强、环保、可复合变压运行、调峰性能好等优势，是我国目前火力发电技术主要的发展方向，并逐步成为电网的主力机组[1,2]。超临界机组采用直流锅炉，具有大时滞、多变量、非线性和强耦合等特点，且考虑到锅炉和汽轮机各自的动态特性，传统的协调控制方法难以保证系统能够快速适应负荷的变化和机组稳定的运行要求[3]。近年来，随着先进控制理论和智能控制算法的不断深入研究，这些算法在超临界单元机组协调控制系统中应用研究也逐渐发展起来，如自适应解耦、神经网络、模糊控制、预测控制等一系列控制方法。文献[4]针对超临界机组简化的负荷—压力动态模型进行了解耦IMC设计，所设计的控制器能够同时实现解耦及IMC，但对于存在最小相位系统的控制回路间难以实现完全解耦，且超调量和调节速度之间相互制约。文献[5]提出了一种解耦与DOBDMC相结合的控制策略，可以解决多变量耦合系统的扰动抑制问题，但构造的解耦补偿器和扰动观测器的结构复杂，阶次较高，不便于工程实现。文献[6]将多变量预测控制方法应用于直流锅炉的协调控制系统，并将其简化为双输入双输出模型，提高了预测模型的精度，但由于预测模型需要在线辨识，因而计算量大，调节速度慢。文献[7]通过机理分析建立了直流锅炉协调控制系统的非线性模型和进行了线性化处理，并对多变量系统实现了完全解耦，但由于燃料量的变化在输出侧的响应较慢，仅采用常规的PID控制器，使得控制品质并未得到很好的改善。

针对上述问题，文中对超临界机组协调控制系统简化的三输入三输出系统数学模型，提出了基于前馈补偿解耦和模糊自整定PID控制相结合的控制方法。首先通过设计的前馈补偿解耦控制器，消除各个通道之间的耦合，只保留主通道的控制特性，实现完全解耦，将多变量系统变成单回路控制系统。然后采用模糊自整定PID控制策略对每个主通道进行控制器的设计，基本原理是依据误差和误差变化率信号在线对PID参数进行修改，提高了控制系统的稳定性，改善了控制品质。该控制方法将多变量复杂系统进行了简化，使得控制器结构简单，调整参数少，易于实现。

1 单元机组协调控制系统

1.1 系统结构

单元机组协调控制系统将锅炉和汽轮机当作一个整体，主要由主控制系统、子控制系统和单元机组对象3个部分组成，其基本组成结构如图1所示。

图1 单元机组协调控制系统基本组成结构

就单元机组而言，锅炉和汽轮机作为一个整体进行协调控制，在满足负荷响应的同时，兼顾内部运行参数的稳定，既要求有较快的负荷响应和一定的调频能力，又保证主汽压偏差在允许的范围内。

1.2 直流锅炉特性

由于在超临界压力下汽包锅炉无法维持自然循环，即汽包锅炉不再适用，因而在超临界机组中一般都是采用直流锅炉，其在工作原理和运行特性上与汽包锅炉有很大的差异。由于直流锅炉没有汽包，加热、蒸发和过热3个阶段受热面没有固定的界限，给水变成过热蒸汽是一次性连续完成的。因此改变燃料量、给水流量和汽轮机调门开度，可作为调节过热汽温、主蒸汽压力和蒸汽流量的手段。因此直流锅炉的协调控制系统可以看作是由机组负荷N、主蒸汽压力PT、中间点焓值(温度)H与汽轮机调门开度μT、燃料量B、给水流量W构成的三输入三输出的多变量控制系统，如图2所示。

图2 直流锅炉的协调控制系统模型结构

其中，输入量分别为汽轮机调门开度μT、燃料量B、给水流量W；输出量分别为机组负荷N、主蒸汽压力PT、中间点焓值(温度)H。由图2可得，协调控制系统的线性化数学模型的传递函数矩阵形式为：

(1)

根据文献[4]，以某厂600 MW超临界机组为研究对象，选用100%负荷工况下的现场运行数据，采用最小二乘法进行系统辨识，建立控制系统的传递函数模型，如下所示。

依据上面辨识所得的系统的传递函数模型，从各个输入量单独阶跃扰动下对输出量的响应曲线来分析直流锅炉的动态特性，并验证所辨识的传递函数模型的准确性，仿真验证的结果如图3所示。

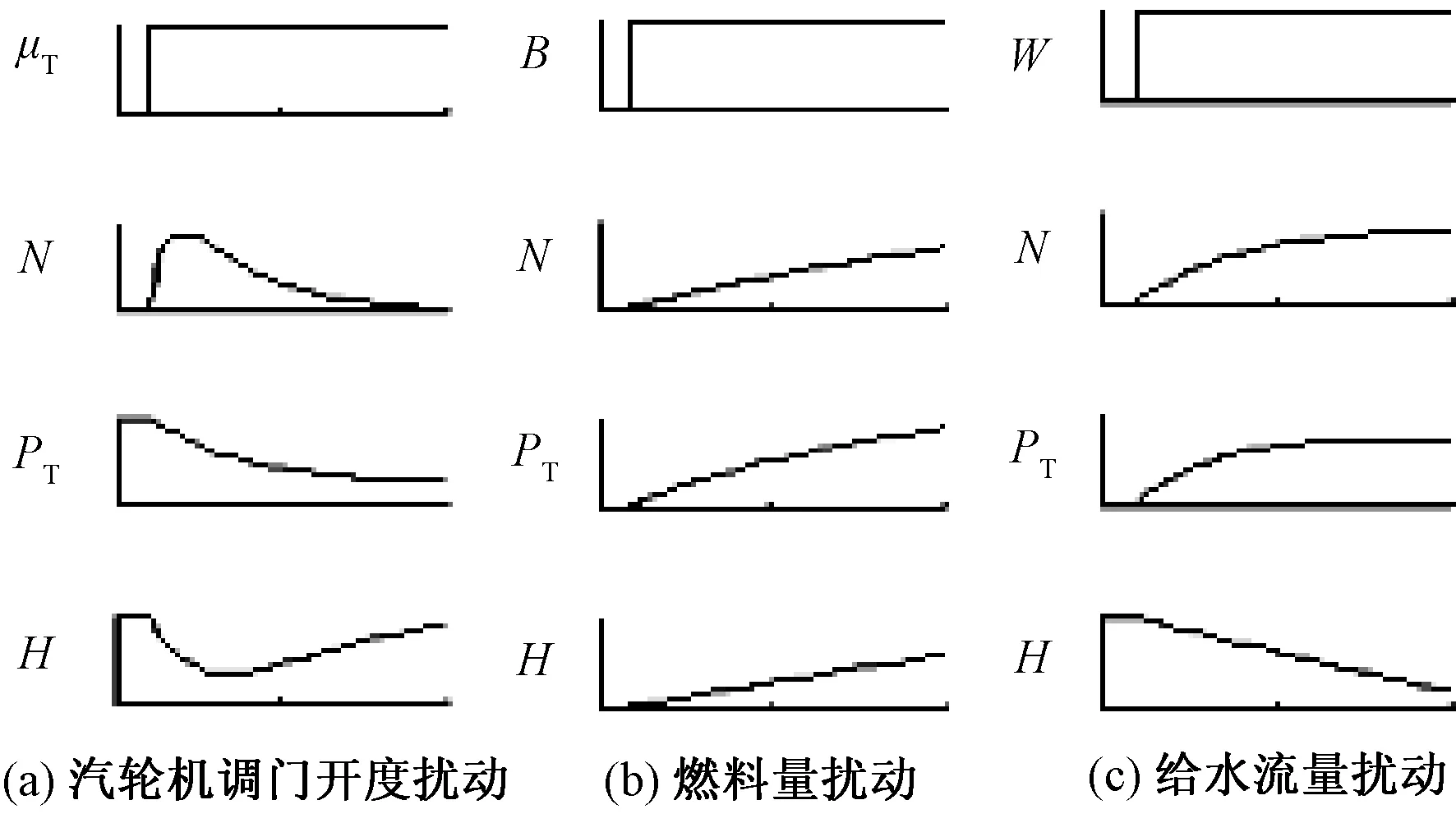
图3 超临界机组的直流锅炉动态特性曲线

由图3可知，直流锅炉被控对象具有很强的耦合性和非线性的特点，并且在汽轮机调门开度、燃料量以及给水流量的扰动下，机组负荷、主蒸汽压力以及中间点焓值(温度)曲线变化趋势与直流锅炉的动态特性基本一致，即所辨识的被控对象模型较准确。

2 解耦补偿器设计

在电力生产过程控制中，大多数的热工被控对象是多输入多输出系统(MIMO)，输入输出的通道之间存在着耦合，即系统的某一个输入与系统的所有输出之间均存在某种关系[8]。在对多变量系统进行控制时，必须同时对多个输入作用进行调整，这无疑增加了调节控制器参数的难度，而且很难保证系统达到很好的控制效果。因此对多变量系统实现解耦控制，把多变量系统转化为多个单回路系统，使之更加易于控制。

2.1 解耦补偿结构

根据系统存在的耦合情况以及需要达到的解耦效果，工程上经常采用前馈解耦方法、反馈解耦方法、对角矩阵解耦方法以及单位矩阵解耦方法等常规解耦方法，另外还有采用模糊解耦控制方法、神经网络解耦控制方法等智能解耦控制。本文中采用前馈补偿解耦方法对系统进行解耦，具体来说是在被控对象G(s)输入端加上一个解耦补偿器D(s)，使得原被控对象和解耦补偿器组成的广义被控对象GD(s)为对角阵。由于解耦补偿器的引入，抵消了被控对象各变量间的耦合影响。多变量系统解耦的基本结构如图4所示。

图4 多变量系统解耦的基本结构

其中，解耦补偿器D(s)的矩阵形式如下：

(2)

式中：D11(s)=D22(s)=D33(s)=1。

2.2 解耦补偿算法

超临界直流机组三输入三输出过程前馈补偿解耦控制系统结构如图5所示。

图5 超临界直流机组前馈补偿解耦控制系统结构

由前馈补偿法[9]，对于u1至y1控制通道，可以把x2、x3视为外部扰动，此扰动可用前馈补偿器来补偿。同样，对于u2至y2控制通道，可以把x1、x3视为外部扰动；对于u3至y3控制通道，可以把x1、x2视为外部扰动，均可用前馈补偿器来补偿。在图5中，D21(s)和D31(s)是通过x1至u1通路中的补偿器，D12(s)和D32(s)是通过x2至u2通路中的补偿器，D13(s)和D23(s)是通过x3至u3通路中的补偿器。即

(3)

解式(3)可以得到解耦装置的数学模型为：

(4)

式中：Gii(s)表示G(s)的主对角线元素，i,j=1,2,…,n。即可得：

(5)

依据上节直流锅炉的协调控制系统的数学模型，可以计算得到解耦补偿器的具体数学模型如下所示：

D11(s)=D22(s)=D33(s)=1

此时，广义被控对象为：

(6)

若设备结构参数或者现场工况发生改变时，首先应该确定被控对象的数学模型，然后利用补偿原理求取解耦装置的数学模型。

2.3 解耦效果验证

在MATLAB/SIMULINK软件平台环境下进行仿真验证，在原来的系统中加入解耦控制器后，分别对汽轮机调门开度、燃料量、给水流量做单位阶跃扰动时，观察机组负荷、主蒸汽压力、中间点焓值(温度)的输出变化曲线，如图6、图7、图8所示。

图6 汽轮机调门开度做阶跃响应时的输出变化曲线

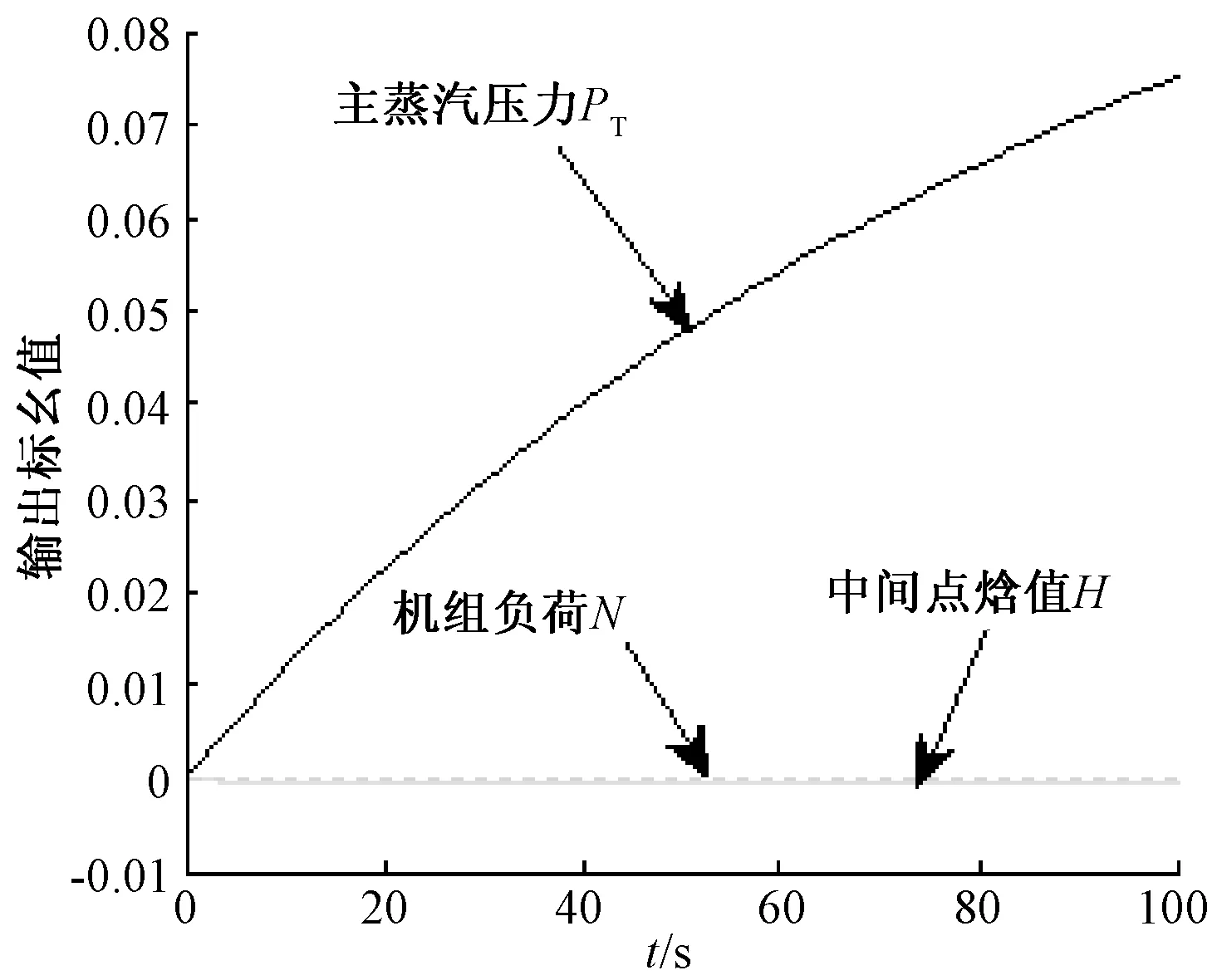
图7 燃料量做阶跃响应时的输出变化曲线

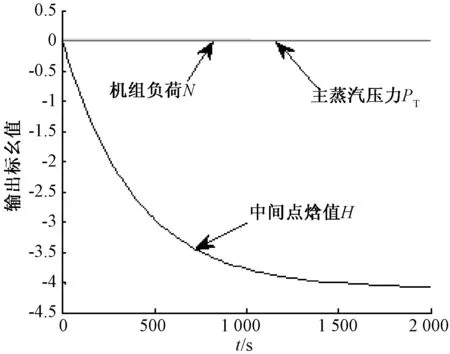
图8 给水流量做阶跃响应时的输出变化曲线

从图中可以看出，当汽轮机调门开度做单位阶跃扰动时，只有机组负荷发生明显变化，而主蒸汽压力和中间点焓值(温度)几乎没有变化；当燃料量做单位阶跃扰动时，只有主蒸汽压力发生明显变化，而机组负荷和中间点焓值(温度)几乎没有变化；当给水流量做单位阶跃扰动时，机组负荷和主蒸汽压力几乎没有发生变化。因此，在加入解耦控制器后，实现了完全解耦，验证了解耦的效果。

3 控制器设计

3.1 模糊自整定PID控制器结构

对于上面已经进行解耦补偿后的超临界机组协调控制系统，每个输出通道均采用模糊自整定PID控制策略。模糊自整定PID控制器的结构如图9所示。

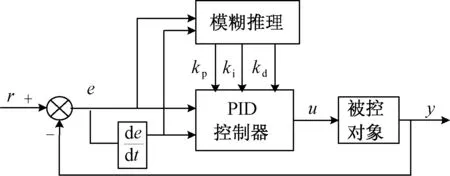
图9 模糊自整定PID控制器结构

离散PID控制算法为

式中：k为采样序号；T为采样时间。

模糊自整定PID基本原理[10]：找出PID的3个参数kp、ki、kd与系统误差e和误差变化率ec之间的模糊关系，在运行过程中不断检测e和ec的变化情况，根据制定好的模糊控制规则来对3个参数在线进行修正，以满足不同e和ec时对控制参数的要求，从而使被控对象有很好的动态性能和静态性能。

3.2 模糊自整定PID设计

本文中采用PI控制器，模糊自整定PI控制算法是在传统的PI算法的基础上，引入了模糊控制算法，利用模糊规则将系统误差e=r(k)-y(k)和其误差变化率ec=e(k)-e(k-1)作为输入，PI控制器参数kp和ki作为输出进行参数的整定。针对kp和ki两个参数分别进行整定的模糊控制规则如表1所示。

表1 kp和ki整定的模糊规则表

kp和ki的整定原则：

(1)当响应在上升过程时(e为P)，Δkp取正，即增大kp；当超调时(e为N)，Δkp取负，即降低kp；当误差在零附近时(e为Z)，共分为3种情况：ec为N时，超调越来越大，此时Δkp取负；ec为Z时，为了降低误差，Δkp取正；ec为P时，正向误差越来越大，Δkp取正。

(2)采用积分分离策略，即误差在零值附近时，Δki取正，否则Δki取零。

将系统误差e和误差变化率ec的变化范围定义为模糊集上的论域[13]，即，其语言值的模糊子集为{负，零，正}，分为简记为{N,Z,P}。由于建立隶属函数受人为因素的影响较大，尽管现在已有多种确定隶属函数的方法，但在实际系统应用中，一般是根据专家的现场经验，加上必要的数学处理而得到隶属函数，最后经过实践检验并逐步修改和完善。经过实验研究表明，用正态分布隶属函数曲线族来描述人进行控制活动时的模糊概念是适宜的，因此最常用的隶属函数是正态分布函数[11]。

设e和ec均服从正态分布，其正态函数计算公式为

(7)

因此可依据上式得出各模糊子集的隶属度，根据各模糊子集的隶属度赋值表和各参数模糊控制模型，应用模糊推理设计PI参数的模糊规则矩阵表，查出修正参数代入下式计算：

kp=kp0+Δkp,k1=ki0+Δki

(8)

其中e和ec的隶属度函数曲线如图10所示。

4 仿真实验及结果分析

针对解耦后的超临界机组协调控制系统3个主通道(汽轮机调开度μT——机组负荷N、燃料量B——主蒸汽压力PT、给水流量W——中间点焓值(温度)H)分别设计模糊自整定PID控制器进行仿真实验，实验中主要对模糊自整定PID控制器与传统PID控制器进行对比分析，验证两者的控制效果。另外对于超临界机组，不同工况下对应的被控对象也会发生变化，因此还需检验模糊自整定PID控制器的鲁棒性。

(1)在汽轮机调开度μT——机组输出功率N通道中，设置PID控制器的初始参数：kp=0，ki=0。变化范围：kp∈[-10,10]，ki∈[-10,10]。同时，根据经验法，对传统PID控制器参数设置为：kp=3.5，ki=2.7，kd=0。仿真时间为10 s。在负荷设定值阶跃变化时，机组负荷的变化曲线如图11所示。

图11 负荷设定值阶跃变化时机组负荷的变化曲线

(2)在燃料量B——主蒸汽压力PT通道中，设置PID控制器的初始参数：kp=0，ki=0。变化范围：kp∈[-20,20]，ki∈[-2,2]。同时，根据经验法，对传统PID控制器参数设置为：kp=10.5，ki=1.2，kd=0。仿真时间为500 s。在压力设定值阶跃变化时，主蒸汽压力的变化曲线如图12所示。

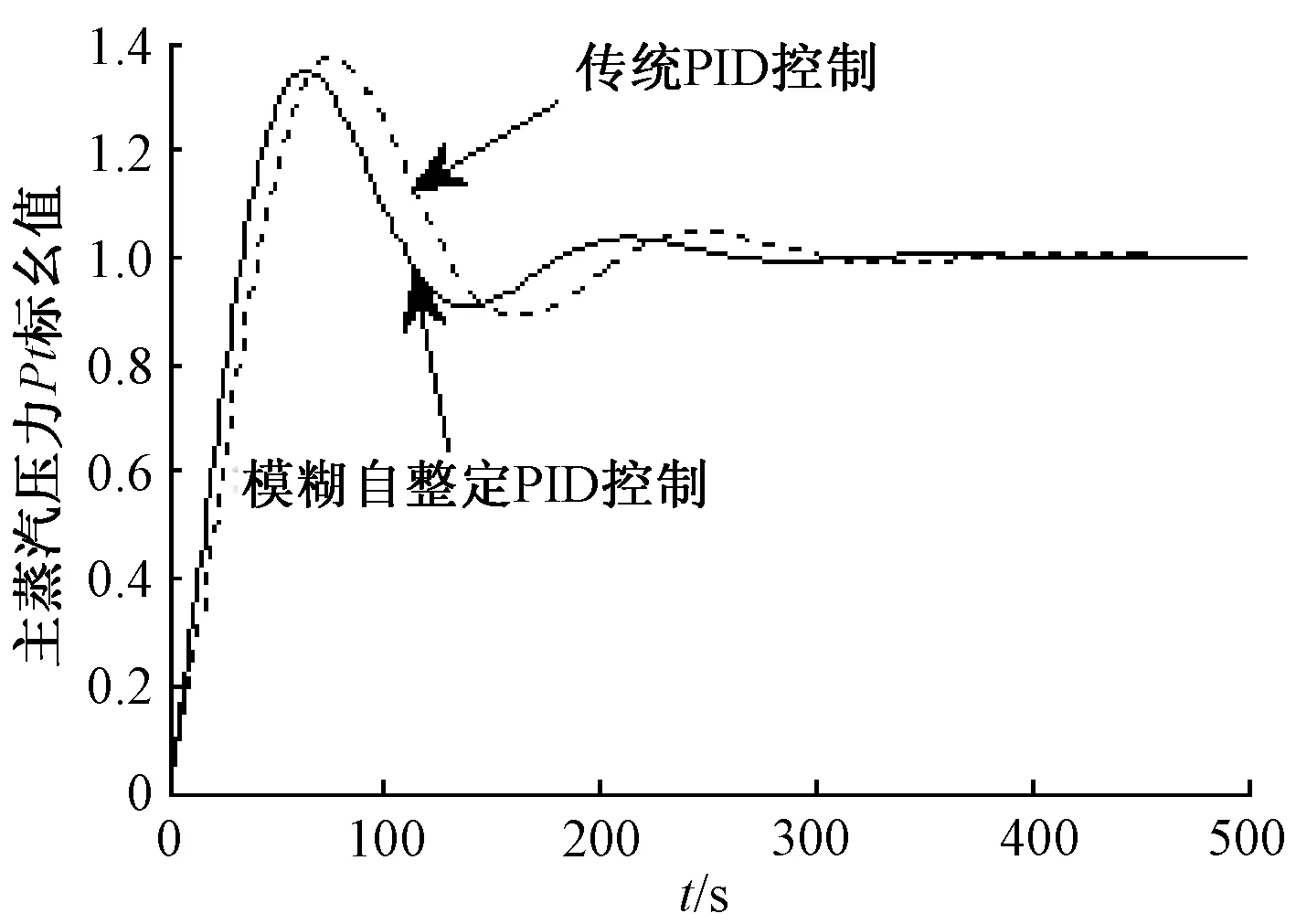
图12 压力设定值阶跃变化时主蒸汽压力的变化曲线

(3)在给水流量W——分离器出口焓值(温度)H通道中，设置PID控制器的初始参数：kp=0，ki=0。变化范围：kp∈[-6,6]，ki∈[-1,1]。同时，根据经验法，对传统PID控制器参数设置为：kp=-3.3，ki=-0.2，kd=0。仿真时间为 500 s。在焓值设定值阶跃变化时，中间点焓值(温度)的变化曲线如图13所示。

图13 焓值设定值阶跃变化时中间点焓值的变化曲线

(4)在实际过程中，由于建模误差无法避免，机组工况发生改变等因素的存在，可能会造成内部扰动，也会影响系统的控制性能。在超临界机组工况变为90%负荷下[4]，直流锅炉的协调控制系统解耦后主通道的数学模型为：

在模糊自整定PID控制器参数不变，在数学模型改变和输出扰动同时发生的情况下，测试机组协调控制系统的控制性能，仿真结果如图14、图15、图16所示。

图14 机组负荷阶跃响应曲线

图15 主蒸汽压力阶跃响应曲线

图16 中间点焓值阶跃响应曲线

通过以上仿真实验可以得出：模糊自整定PID控制器使超调量变小、调节时间缩短、稳定性提高。对比于标称状况，虽然控制性能有所下降，但可以在模型失配情况下克服扰动，较快地将系统输出维持在给定值，即具有良好的鲁棒性。

5 结论

本文针对超临界直流锅炉对象具有耦合性、多变量、非线性等特点，将前馈补偿解耦算法和模糊自整定PID控制策略相结合，应用于超临界机组的协调控制系统中。首先运用前馈补偿的解耦算法对600 MW的超临界机组模型进行了解耦处理，消除了支路通道的耦合影响，保持了主通道不发生变化，实现了完全解耦。然后采用模糊自整定PID控制算法对解耦后的系统进行控制，使超调量变小、调节时间缩短、稳定性提高，达到了很好的控制效果。最后进行了模型失配情况下的仿真实验，结果表明，抗扰能力强、控制品质良好，具有很好鲁棒性。但本文所用模型是对历史数据进行离线辨识的，在不同的运行工况下，系统模型会发生变化，因而为适应模型的变化，控制器参数也需做相应调整，为更好提高系统的控制性能，还需做进一步的研究。

参考文献：

[1]杨优生, 王东风, 智丹. 基于动态模糊神经网络的机炉协调系统建模[J]. 电力科学与工程, 2017，33(7):58-63.

[2]梁杨. 基于遗传算法辨识的超超临界机组协调控制系统[D]. 保定：华北电力大学, 2011.

[3]江溢洋, 王东风. 基于改进逆向解耦的超超临界机组机炉协调控制[J]. 华北电力大学学报(自然科学版), 2014, 41(5):89-94.

[4]笪凌云, 沈炯, 李益国,等. 基于解耦和 DOB 的 DMC 在机炉协调控制系统中的应用[J]. 东南大学学报(自然科学版), 2015, 45(5):910-917.

[5]项丹, 刘吉臻, 李露. 基于多变量解耦内模控制的机组协调控制系统设计[J]. 热力发电, 2015，44(2):69-73.

[6]王富强, 李晓理, 张秋生,等. 直流锅炉超超临界机组协调系统多变量预测控制方法[J]. 热力发电, 2016, 45(4):48-53.

[7]秦志明, 张栾英, 谷俊杰. 直流锅炉单元机组协调控制系统的研究与设计[J]. 动力工程学报, 2016, 36(1):16-21.

[8]郭献军, 席原, 王周梅,等. 基于类前馈补偿的模糊PID控制在超超临界单元机组协调控制系统的应用[J]. 现代电力, 2012, 29(4):67-72.

[9]刘鑫屏, 田亮, 秦治国. 一种工程化的协调控制系统解耦控制方案[J]. 电力科学与工程, 2014，30(1):74-78.

[10]刘金琨.智能控制(第4版)[M].北京：电子工业出版社，2017.

[11]孙海蓉, 耿军亚, 王蕊. 凝结水节流模糊参数自整定PID控制器[J]. 热力发电, 2017, 46(2):75-80.

[12]WANG Y, YU X. New coordinated control design for thermal-power-generation units[J]. IEEE Transactions onIndustrial Electronics, 2010, 57(11):3848-3856.

[13]YU T, CHAN K W, TONG J P, et al. Coordinated robust non-linear boiler-turbine-generator control systems via approximate dynamic feedback linearization[J]. Journal of Process Control, 2010, 20(4):365-374.