红黑树在含风电电力系统可靠性评估中的应用
2018-05-17童煜栋
栗 然, 童煜栋
(新能源电力系统国家重点实验室(华北电力大学),河北 保定 071003)
0 引言
随着风电机组单机容量和风电场规模的不断增大,迫切需要研究大型风电场并网对发输电系统的影响及其带来的风险,全面评估风电的价值[1]。风险与可靠性描述着同一事实的两个方面,更高的风险意味着更低的可靠性[2]。提高可靠性可以降低系统的风险。如何有效地、快速地评估含风电电力系统的可靠性是一个重要的课题。
电力系统的可靠性评估主要分为确定性评估和概率性评估,其中概率性评估分为解析法和蒙特卡洛模拟法(MCS)[3]。MCS的优点在于,在计算精度一定的情况下,元件数目的多少不影响该方法的抽样次数,且思路简单,便于编程[4]。但是在MCS中,每一次状态的分析和优化过程都占用了大量计算时间,随着精度的上升和风电的并网,计算时间迅速增加。计算量与估计精度的平方成反比,因此,减少方差可以提高估计精度[5]。文献[6]采用等分散抽样减小方差,提高模拟精度,大幅减少了抽样次数;文献[7]将自适应重要抽样应用在发输电系统可靠性评估中,在元件故障概率较小时能显著提高可靠性评估的计算效率;文献[8]结合了重要抽样和分层抽样,提出分层均匀抽样;文献[9]采用重要抽样改进拉丁超立方抽样,提高抽样效率;文献[10-12]提出基于粒子群支持向量回归法的电网可靠性评估的新方法,证明粒子群、支持向量机在电网可靠上的应用价值;文献[13]提出交叉熵结合动态故障集,使用索引链表来记录抽样得到的故障和分析结果,通过查询已经分析的样本来减少重复分析,但没有考虑风电场数量对计算时间的影响。
评估含风电的发输电系统,需要建立风电场出力模型。文献[14]以威布尔分布为基础,考虑风电机组的尾流效应,建立了风电机组的三状态模型。文献[15]运用k-means聚类法处理风电场功率输出时间序列,得到风电场出力的多状态概率分布模型。
本文考虑风速的尾流效应,采用等分区间建立风电场的多状态出力模型,提出分别采用红黑树、散列表这两种数据结构来构造动态故障集,以包含数个风电场的IEEE-RTS79系统作为算例,分析两种数据结构各自在计算时间上相对于MCS的优势,并在不同的方差系数、风电场数量和风电场状态数下,分别比较两种数据结构在指标误差、计算时间上的差异。
1 风电场的多状态模型
本文通过蒙特卡洛模拟法获得风电场出力,并将单个风电场的出力等效为多状态发电机组。具体步骤如下:
步骤1:以威布尔分布建立风速模型,获得风速序列;
步骤2:对风电机组建立正常、故障和降额三状态模型,并进行序贯蒙特卡洛模拟;
步骤3:根据风电机组运行状态和尾流效应,计算每个风速下,每台风电机组的风速;
步骤4:通过各机组风速计算各机组的实际出力,从而获得整个风电场的出力序列。
步骤5:风电场出力范围均分为N个区间,每个区间的出力为该区间内出力的均值,每个区间的概率为该区间中出力的总持续时间与风电场出力持续总时间的比值。划分完毕后就能获得风电场的多状态出力。
2 含风电场的发输电系统可靠性评估
2.1 非序贯蒙特卡洛法
非序贯蒙特卡洛法又称状态抽样法,其依据为:一个系统状态是所有元件状态的集合,每个元件状态可由出现在该状态的概率进行抽样决定。对于一个两状态的元件i,其停运概率Pf、状态Si可表示为
(1)
(2)
式中:λi和μi分别为元件i的停运率和修复率。
含m个元件的一个系统抽样状态为S=(s1,s2,…,sm),当抽样得到足够数量,状态S的抽样频率可作为其概率的无偏估计:
(3)
式中:NS为抽样次数;n(S)为状态S的次数。
指标的期望为
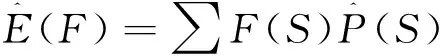
(4)
式中:F(S)为指标在状态S下的值。
系统指标的不确定性可以通过样本均值的方差度量,其定义为
(5)
式中:Fk为第k次抽样得到的指标。
蒙特卡洛模拟的精度可以用方差系数描述,表示为
(6)
2.2 电力系统元件停运模型
电力系统常规元件包括输电线、发电机等,这些元件通常采用正常、停运的两状态模型。负荷采用多级负荷模型。
2.3 最优切负荷
当电力系统中的元件停运或者风电场出力变化时,系统可能需要切负荷甚至发生解列。本文在调度发电机时,优先使用风电。最优切负荷模型如下:
目标函数为
(7)
约束条件为
PG-PD+PC=B0δ
(8)
(9)
PGimin≤PGi≤PGimax,i∈NG
(10)
0≤PCi≤PDi,i∈NB
(11)
|Pij|≤Pijmax,i,j∈NB
(12)
Pij=-bij(δi-δj)
(13)
式中:ND为带负荷节点的集合;NG为带发电机节点的集合;NB为所有节点的集合;PG为包括等效风电场在内的发电机出力向量;PD为有功负荷向量;PC为负荷削减向量;δ为节点电压相角向量;B0为节点导纳矩阵;PGi为节点i上发电机的有功出力;PCi为节点i上的切负荷;PDi为节点i上的有功负荷;PGimax、PGimin分别为节点i上发电机的出力上限和下限;Pij为支路ij的有功潮流;Pijmax为潮流上限;bij为支路ij的导纳;δi为节点i的电压相角。
3 动态故障集
使用动态故障集的主要目的为存储状态、查找状态、避免重复分析状态。MCS的每次抽样能获得该次的元件故障状态和风电场出力,在不使用动态故障集时,需要对每次抽样得到的状态和出力都进行复杂繁琐的分析,这些分析包括了检查系统是否已经解列;负荷、发电是否平衡;进行简单的潮流计算,并判断是否有潮流或电压越限;若有可能需要切负荷,则运行最优切负荷程序。最优切负荷程序约束众多,即使采用了直流潮流和线性规划,仍然会耗费大量计算时间。若为了减小误差而采用交流潮流,则耗费的时间将更加庞大。因此,文献[13]提出了采用动态故障集,即在MCS的计算过程中开辟一个内存空间,建立索引链表,将已经抽样并分析的状态和结果存储在索引链表中,以索引链表的查询来替代重复且费时的分析。在每次抽样得到新的故障状态后,首先查询已存储的状态,若查询成功,则直接读取切负荷计算结果;否则对新状态进行分析,并存储结果。
在计算机数据结构中,数据的存储和查询除使用索引链表之外,更普遍的结构是红黑树和散列表。两种数据结构均能实现高效地存取数据,但各有优劣,需要根据实际的应用场景进行选取。以下将分别介绍本文中数据的定义和这两种结构的特点。
3.1 故障和失负荷信息的存储结构
故障抽样总次数为NS,第i次抽样可以获得一个故障状态Si。Si为0、1组成的向量,由Si组成的故障状态集合为稀疏矩阵。为节省内存空间,本文对每次抽样中的m个元件从1到m依次编号,将编号存储为向量FAULT以替代故障状态Si,同时存储故障阶数NUM、数个风电厂的出力向量PW和切负荷信息CSTATUS。在MATLAB中定义类Data,包含成员变量FAULT、NUM、PW和CSTATUS。
3.2 基于红黑树的动态故障集
定义:一颗二叉树若满足如下性质,则称为红黑树:
(1)每个节点不是红色就是黑色;
(2)根节点为黑色;
(3)如果节点是红色,则其子节点必须是黑色;
(4)任一节点至NULL(树尾端)的任何路径,所含黑节点数相同。
一颗以整数作为数据的红黑树结构如图1所示。图中,Data为节点的数据;Color为节点颜色,分别为红色r和黑色b;Left和Right分别为指向左子树和右子树的指针,简写为L、R。
红黑树是一种平衡的二叉搜索树,查找的时间复杂度小于O(log2N),N为树的节点数。平衡的大致意义是没有任何一个节点深度过大。普通的二叉搜索树的查询效率与树的深度有关,当左右子树的深度差较大时,查询效率与链表(时间复杂度O(N))接近。包含红黑树在内的平衡二叉树,在插入和删除节点时耗时较长,但是可以避免高度不平衡的情况,一般而言搜索时间可以节省25%左右。
红黑树的查找、插入和删除等基本操作详见文献[17]。红黑树的构造要求节点中的Data是有序的。如果Data为数,则对于任意一个节点,其左子节点中的数总是小于右子节点的数。因此需要在MATLAB中为类Data定义顺序,按以下步骤确定节点大小:对于任意的节点甲和乙:
(1)若节点甲的NUM小于节点乙,则节点甲更小;
(2)若节点甲的NUM大于节点乙,则节点甲更大;
(3)若节点甲的NUM等于节点乙,则继续比较PW,转步骤(4);
(4)依次比较PW的各个风电场的出力大小,若完全相等,则继续比较FAULT,转步骤(7);
(5)若先发现节点甲PW的元素更大,则节点甲更大;
(6)若先发现节点甲PW的元素更小,则节点甲更小;
(7)依次比较FAULT的各个故障编号的大小,若完全相等,则两个节点完全一致;
(8)若先发现节点甲FAULT的元素更大,则节点甲更大;
(9)若先发现节点甲FAULT的元素更小,则节点甲更小。
如图2所示为本文红黑树节点的结构。

图2 红黑树节点的结构
3.3 基于散列表的动态故障集
常用的数据搜索方式除了红黑树外,还有散列表(Hashtable),又称哈希表。如图3所示为散列表的结构。
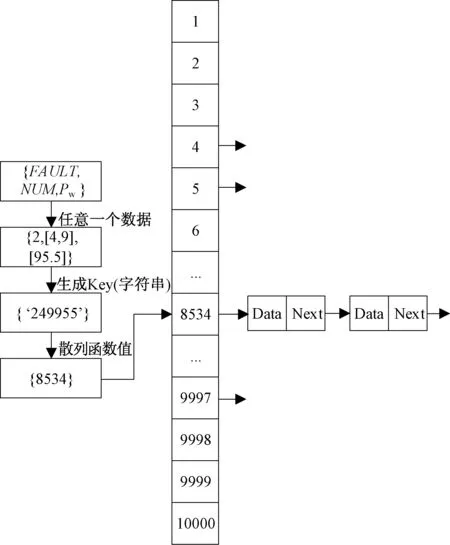
图3 散列表的结构
散列表现为常数平均时间,时间复杂度为O(1)。散列表可以看作数组,对某个数据项的访问和其他数据项完全独立。为了访问某个数组元素,需要定义数据data的键(key),使用散列函数将键作为实参,并返回一个指明元素位置的整数值。散列表不需要知道Data的顺序和大小,不会有类似红黑树的排序所消耗的时间,但会多出计算散列函数的时间,各有利弊。本文将Data转换为字符串作为键,所用的散列函数参考文献[16],并使用拉链法来解决不同的数据项映射到相同的位置的问题。不同的故障和风电场出力将会有不同的散列函数值,但也存在不同的Data计算得同一值的可能性,即产生冲突。拉链法通过单链表,将冲突的故障存放在单链表中。
4 算例分析
本文使用IEEE-RTS79测试系统,该系统包括24个节点,32台发电机,38条线路,总装机容量 3 405 MW,年负荷峰值2 850 MW,电气接线如图4所示,测试系统的线路、发电机的强迫停运率和负荷数据见文献[1]。风电场布局见文献[14],相邻风机水平距离为350 m,垂直距离为850 m。每个风电场包含风电机135台,分为9组,每组为一行,一组15台风电机。每台风电机额定功率取1.2 MW,停运率取0.05,降额率取0.05,停运修复率58.4,降额恢复率43.8,叶轮高60 m,叶片半径37 m。威布尔分布的形状参数取2.02,尺度参数取8.03。切入风速3 m/s,切出风速25 m/s,额定风速12 m/s。风电场接入节点设置为系统的23节点。评价指标选取为电量不足期望(EENS)和切负荷概率(LOLP),收敛条件为EENS的方差系数η。
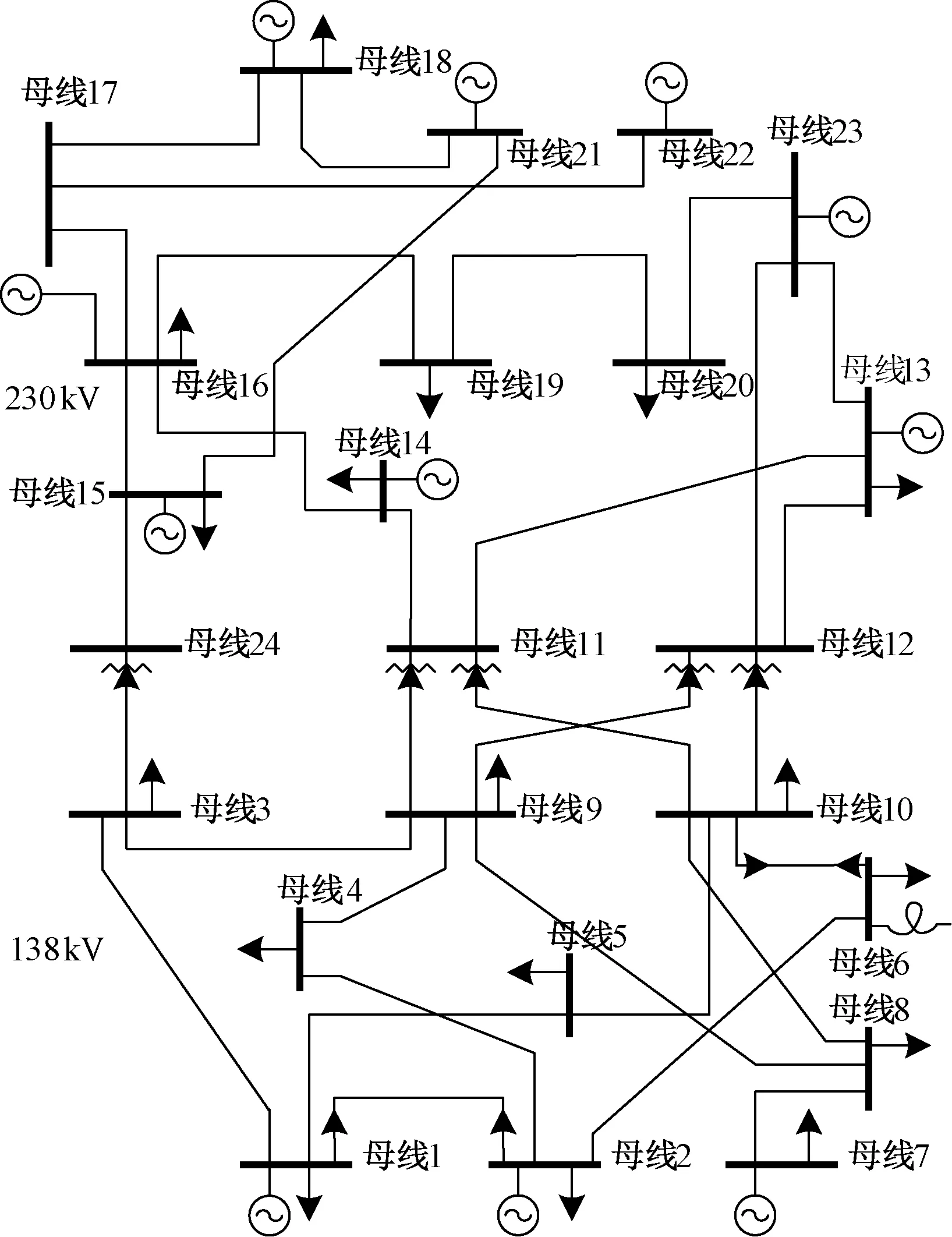
图4 IEEE-RTS79电气接线图
4.1 3种方法的评估结果和计算时间对比
表1所用系统的风电场数量为1、风电场出力等效状态数为5,η为0.1,将未采用动态故障集的MCS方法和采用红黑树、散列表的方法进行对比,分析在迭代次数、指标、计算时间上的差异。由表1可知,在约20 000次左右的抽样次数下,采用红黑树后的计算时间仅为MCS的22.89%,采用散列表后的计算时间仅为MCS的21.02%,可见使用动态故障集后,显著提高了可靠性评估的速度。红黑树的指标EENS相对MCS方法的指标偏离了4.37%,散列表偏离了5.39%,均小于方差系数的10%,都在可接受的范围之内。红黑树的指标LOLP相对MCS方法的指标偏离了5.02%,散列表偏离了5.19%,也相差不大。因此,在合适的条件下,采用红黑树或采用散列表的动态故障集均能够有效改善含风电电力系统的可靠性评估速度,并对评估指标的误差影响不大。

表1 3种方法的评估指标和计算时间
4.2 风电场数量对计算时间的影响
增加风电场的数量,系统的23节点上变为3个同样规模的风电场,风电场等效状态数保持为3个,η保持为0.1,结果见表2。
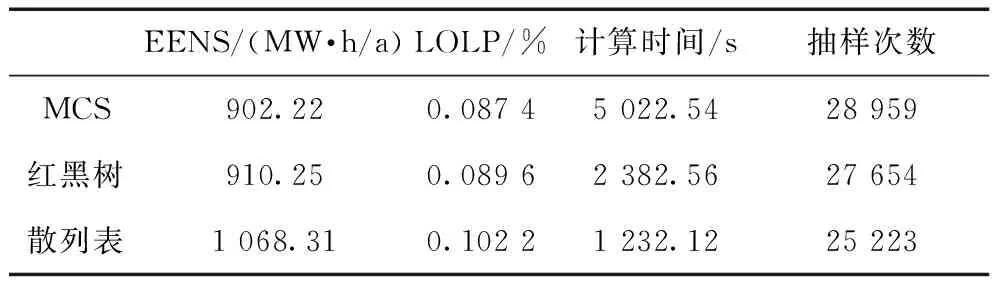
表2 有3个风电场时的评估指标和计算时间
在表2中,散列表的时间为MCS的24.53%,比表1中的21.02%大,这是由于风电场数量增加的影响,转换得到的字符串变长,相应的散列函数的计算时间也更长。对比表1的结果,能发现随着风电场数量的增加到3个,MCS的时间增加了38.83%,红黑树的时间增加了87.65%,散列表的时间增加了62.05%。红黑树的计算时间增幅最大。主要原因是:红黑树在查找时需要根据Data为新旧节点排序,随着Data中风电场出力向量PW长度的增加,使得大量时间耗费在风电场出力大小的比较上,而散列表的散列函数受此影响更小。
虽然散列表的时间更短,但是表2散列表的结果中,指标EENS偏离MCS达到18.41%,LOLP的偏离也达到16.93%,可能的原因为Data到key的转换函数和散列函数在设计上存在不足。随着样本规模扩大,散列冲突愈发严重。因此,在包含风电的电力系统可靠性评估中,随着所需记录的数据种类与数量变多,设计合适的散列表和散列函数可以比需要排序的红黑树实现更快的查询,但也面临着无法预知采用何种key转换函数和散列函数更优的问题。
本文考虑的是大型风电场,因此数量不会太多,只讨论到单个节点上最多10个风电场。图5为随着风电场数量增加,红黑树方法和MCS的计算时间的变化,以及红黑树方法占两者总时间比例的变化,图6为两者抽样次数的变化。由图5中两种方法各自的变化趋势可见,风电场总数越多,则计算时间的增幅越大;在风电场数量增加到4个或更多之后,红黑树相对MCS的时间优势基本上保持在60%到70%,没有继续劣化。
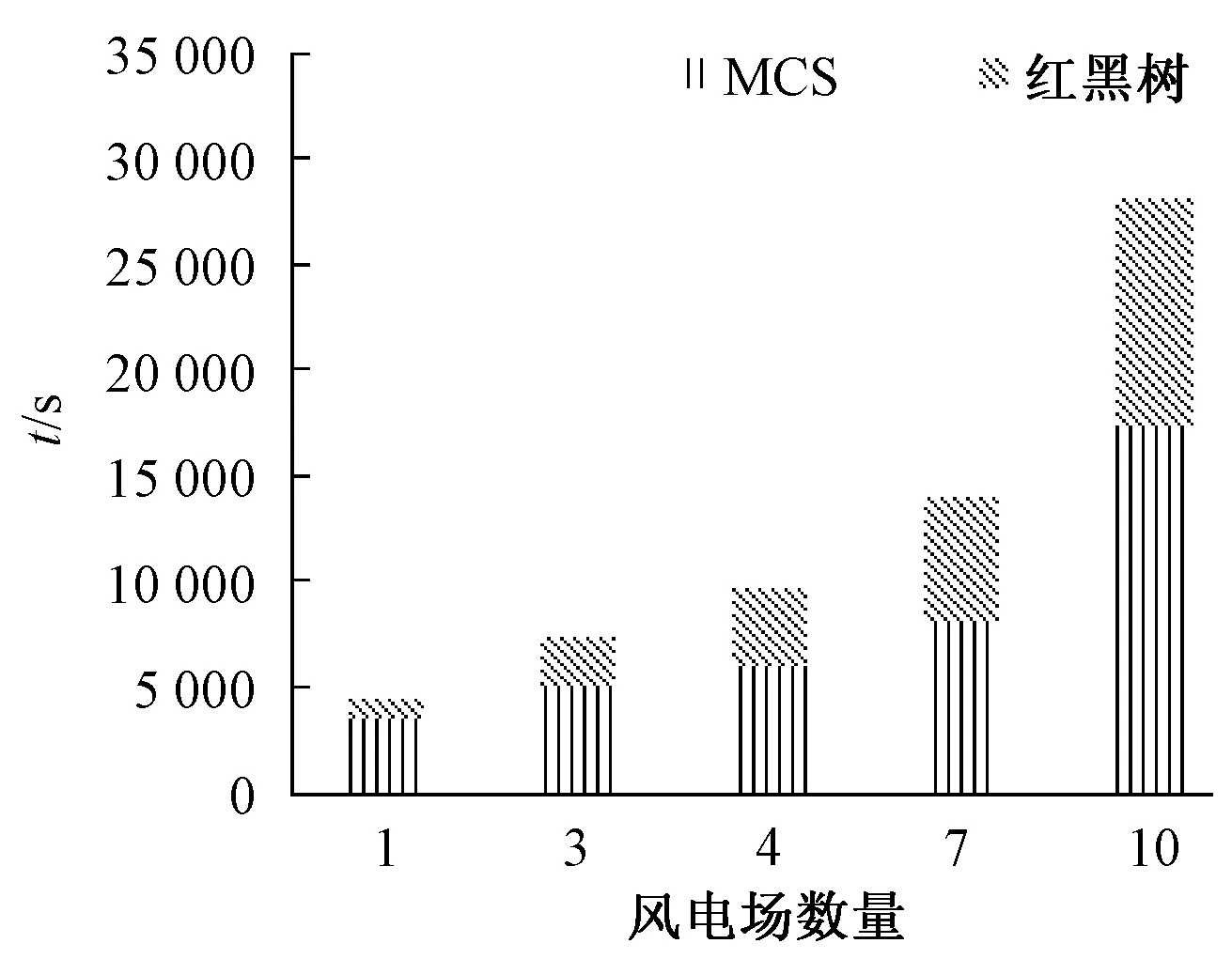
图5 风电场数量对红黑树计算时间的影响
由图6可知,当风电场数量增加到4个以上,红黑树相比MCS总是以更少的抽样次数就能满足方差系数,因此尽管之前的分析中红黑树性能明显受到风电场数量增加的影响,但MCS抽样次数的增速大于红黑树,因此最终红黑树的计算时间占总时间的比例稳定在60%~70%。
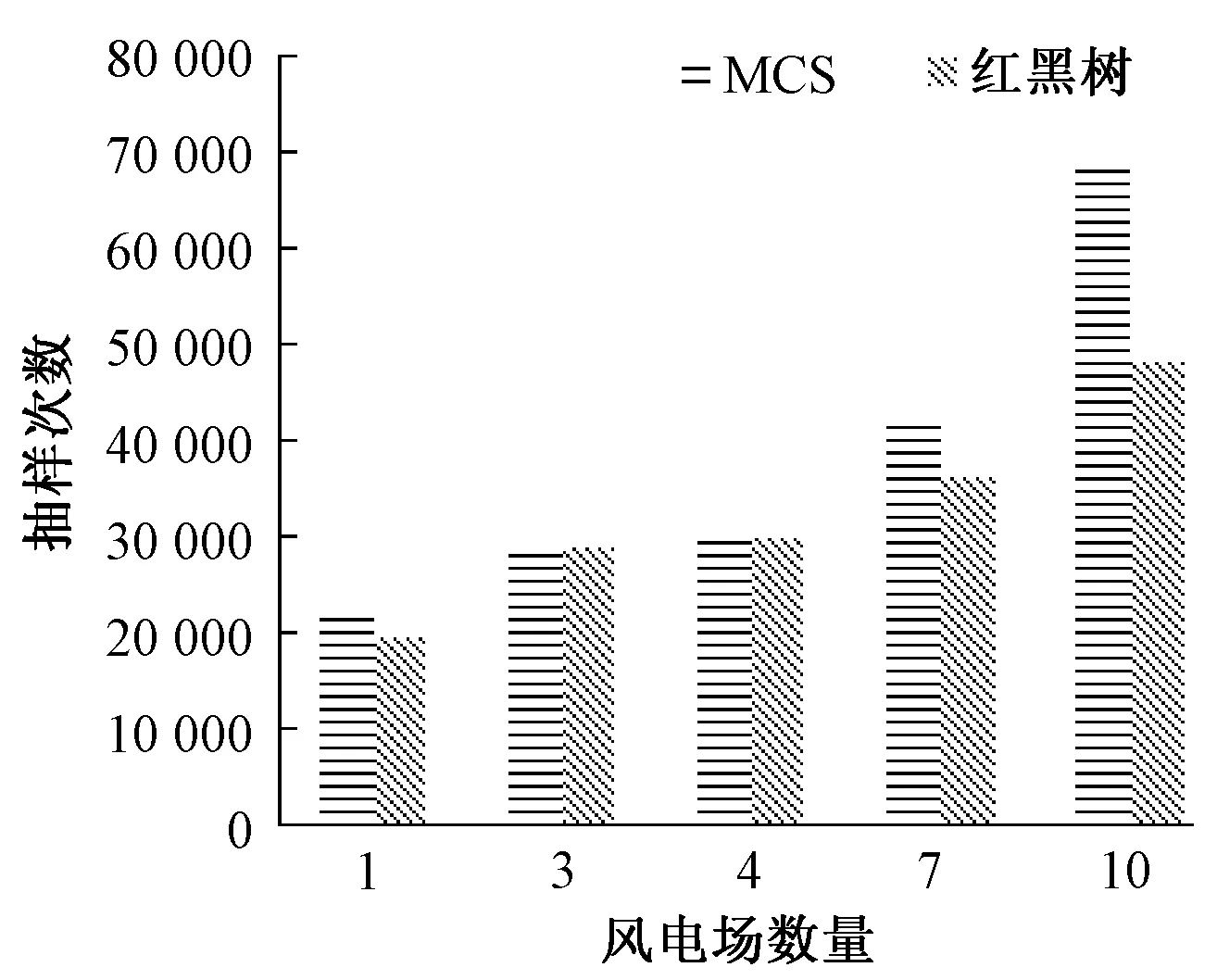
图6 风电场数量对红黑树抽样次数的影响
4.3 风电场状态数对计算时间的影响
表3中,η保持为0.1,风电场数为1。对比表1,在风电场等效状态数增加后,抽样次数显著较少,使得3种方法的计算时间均显著减少。红黑树、散列表相对MCS的时间分别为24.22%、23.81%,与表1中的结果相差很小。与风电场数量增加时不同,风电状态数并没有使红黑树性能明显下降,风电状态数与红黑树和散列表的性能关系不大。
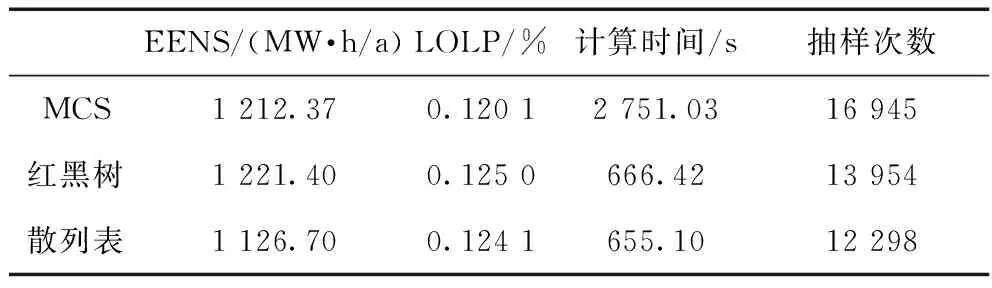
表3 风电场状态数为10的评估指标和计算时间
4.4 精度对计算时间的影响
对不同精度下的计算时间进行比较,风电场数量为1,风电场出力等效状态数为5,结果见表4。表4列出了不同精度下,红黑树、散列表各自相对MCS的时间比。在抽样次数上,3种方法相差不多。在方差系数减小到0.075时,红黑树和散列表的时间比最高,接近30%。而当方差系数减小到0.05时,红黑树和散列表的时间比减少到20%。可见,在由计算精度导致的规模增大时,红黑树和散列表都能够维持不错的减时的效果。散列表的散列冲突依然存在,且在不同的精度下,EENS偏离程度不一,精度0.1时偏离了5.39%;精度0.075时,偏离了23.27%;精度0.05时偏离了3.84%。
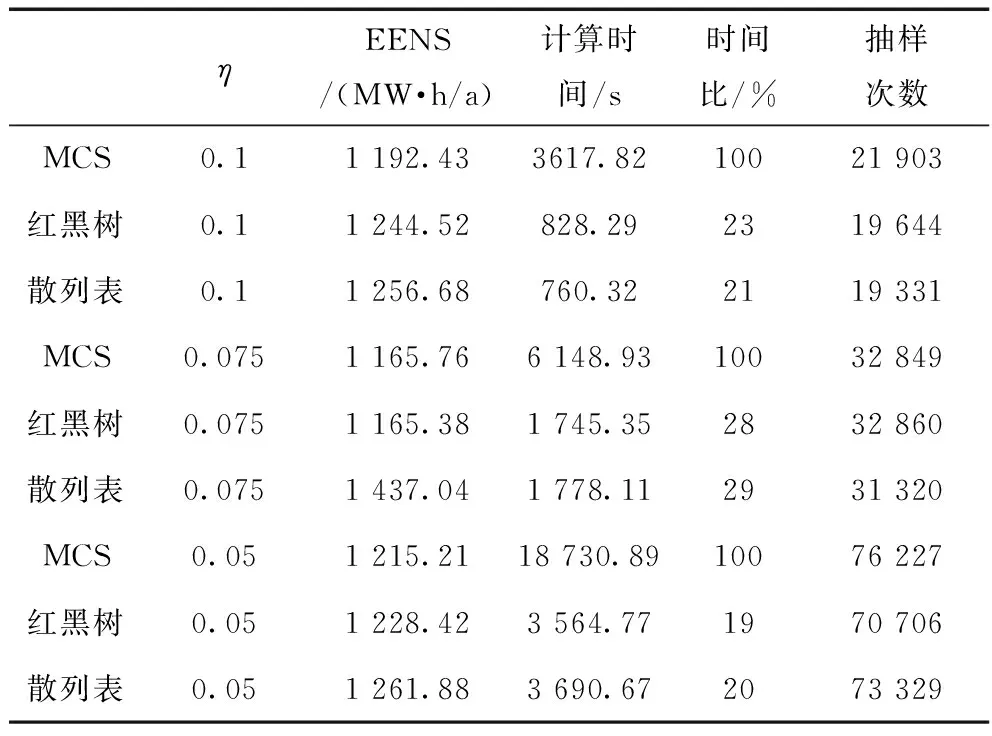
表4 不同精度下的评估指标和计算时间
当计算精度继续增加,故障集的规模迅速扩大,精度小于0.05时,需要数十万次以上的迭代。散列表和红黑树的计算时间在不同的故障集规模下始终保持一致。从计算时间的绝对值差上看,相对于MCS,红黑树和散列表节省的时间会随着故障集规模的增大愈发突出。
5 结论
本文提出采用红黑树优化的动态故障集,加速传统非序贯蒙特卡洛法的计算速度。同时对比了采用散列表优化的动态故障集。在包含数个风电场的IEEE-RTS79测试系统中进行算例分析,得到以下结论:
(1)采用了红黑树的动态故障集与采用散列表的动态故障集在蒙特卡洛模拟中的应用使得计算时间显著下降80%左右;
(2)当风电场数量较多时,红黑树的加速效果会明显下降,但依然优于MCS,散列表的加速效果保持不变;
(3)风电场等效状态数对红黑树、散列表加速效果的影响不明显。风电场等效状态数增加能够显著减小抽样次数,使得MCS的计算时间减少。
(4)散列表虽然理论查找性能强于红黑树,但是受到散列函数的制约,散列函数的计算时间使得散列表的实际查找性能不一定优于红黑树。当预先设计的散列函数和key转换函数不合适时,会导致难以预期的散列冲突,使可靠性指标偏离正确值。
参考文献:
[1]蒋程,刘文霞,张建华,等.含风电接入的发输电系统风险评估[J].电工技术学报,2014,29(2):260-270.
[2]黄旭.含异步化同步发电机的电网可靠性评估模型研究[D].重庆:重庆大学,2012.
[3]杜江.基于蒙特卡洛法的电力系统可靠性评估算法研究[D].杭州:浙江大学,2015.
[4]张巍峰.基于蒙特卡洛法的电力系统可靠性评估算法研究[D].天津:天津大学,2014.
[5]王立雪,孙聚波,徐平峰.蒙特卡罗方法及其方差缩减技术比较分析[J].长春工业大学学报,2015,36(5):485-490.
[6]陈文婕,刘晋,周云海,等.基于等分散抽样法的配电系统可靠性评估[J].陕西电力,2010,38(6):23-27.
[7]谢绍宇,王秀丽,王锡凡,等.自适应重要抽样技术在发输电系统可靠性评估中的应用[J].电力系统自动化,2010,34(5):13-17.
[8]黄江宁,郭瑞鹏,赵舫,等.电力系统可靠性评估中的分层均匀抽样法[J].电力系统自动化,2012,36(20):19-24.
[9]张巍峰,车延博,刘阳升.电力系统可靠性评估中的改进拉丁超立方抽样方法[J].电力系统自动化,2015,39(4):52-57.
[10]王景辰,李孝全,杨洋,等.基于蒙特卡洛法和最小二乘支持向量机的复杂电力系统可靠性评估[J].华东电力,2013,41(5):1001-1004.
[11]龚兰芳,张昱.电网可靠性评估的PSO-SVR评估模型[J].计算机仿真,2011,28(7):196-199.
[12]李孝全,黄超,徐晨洋,等.基于改进PSO-LSSVM和蒙特卡洛法的电力系统可靠性评估[J].河海大学学报(自然科学版),2016,44(5):458-464.
[13]许鹏程,陈启,刘文霞,等.引入交叉熵与动态故障集的含风电大电网可靠性评估[J].电力系统自动化,2016,40(13):28-34.
[14]张硕,李庚银,周明.含风电场的发输电系统可靠性评估[J].中国电机工程学报,2010,30(7):8-14.
[15]仇国兵.基于聚类的复杂地形下风电场输出功率概率分布建模[D].北京:华北电力大学,2014.
[16]邓俊辉.数据结构:C++语言版.第2版[M].北京:清华大学出版社,2012.
