基于事故链和Markov过程时滞电力系统稳定性分析

孟德强

(国网冀北电力有限公司，北京 100052)

0 引言

随着时滞的存在使电力系统稳定分析和控制变得愈加复杂，已成为系统不稳定及性能变差的根源[1-3]。因此，对时滞稳定性的研究需要更进一步。

目前已有一些理论成果，主要分为两大类：

(1) 频域法。文献[4-7]基于Rekasius变换来求解系统时滞稳定上限。文献[8]通过复频域系统求解电力系统时滞的稳定性。具体方法是将系统特征根方程转为多项式求解复频域虚轴上的解，忽略实数的值。

(2) 时域法。文献[9-11]分别将Finsler引理、Park不等式、Moon不等式和Fridman广义模型变换方法与李雅伏诺夫稳定性分析理论相结合，求解系统时滞。文献[12]在文献[9-11]的基础上进一步分析得出保守性更小的解，并拓展得到时域上更稳定的解法。

目前随着电网的规模不断扩大，容量不断增加，系统的复杂性也随着增强，所以当某一地区放生故障时，有可能导致连环故障。在这种情况下，电网时滞稳定性研究更加重要。因此，本文提出了基于事故链和马尔科夫动态过程的时滞电力系统稳定性分析方法。这种方法能够在事故链方程的基础上求解时滞稳定的上限，还能在物理意义上对电力系统的时滞稳定性进行分析，从而能更好地解决系统稳定性问题。并且，本文根据这一算法给出了仿真验证。

1 事故链的基本理论

事故链理论认为区域事故一般由一条事故链引发其他事故链造，一条事故链可以表述为：

Lj={Lj1→Lj2→Lj3→…→Ljn}

(1)

式中：Lj是一条事故链；Lji代表Lj的第i个环节；n代表中间环节的个数。由电力系统故障分析可知：一条线路故障引发其他线路的故障，具体过程是：通过某条线路预测下一条故障线路，观察其频率振荡特性，判断是否失稳。本文主要基于潮流转移生成事故链。实际电力系统发生连锁故障时，相邻两级故障间的时间跨度一般长达数分钟甚至数十分钟，其间系统暂态过程基本结束[13-14]。

电力系统某条运行线路发生故障时会被系统中切除，这条线路上的原负荷会发生转移，这个过程可能会引起继电保护设备误动作而扩大故障范围。本文分别采用α、β、γ来表示潮流变化率，过负荷裕度以及故障线路与预测线路之间的耦合度，且中间环节预测指标用φ来表示，该指标决定了事故链的下一级的故障线路。

假定系统中线路i发生了故障，线路i中通过的潮流为Si，则α、β和γ的计算式[15-18]如下：

(2)

(3)

(4)

式(4)中：Si(tf)代表事故前线路i中通过的潮流；Sj(tf)代表事故前线路j中通过的潮流；Sj(tb)代表线路i发生事故后线路j中通过的潮流；Sjmax代表线路j中允许流过的最大潮流。

中间环节预测指标φ的定义为：

(5)

式中：φij的值代表线路i对线路j的影响率，所以式(6)可以计算出由潮流转移引起的状态转移的概率：

(6)

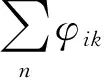
通过上述分析可以得出，电力系统某一条线路故障，会引发其他线路故障，且引发条件只跟上一级事故链有联系。基于以上条件，假设系统模态为rt=r(t)，它取值于有限集合S={1,2,…,s}，是齐次Markov过程。对于事故链L={L1→L2→L3→…→Ln}，首先将任意环节Li(i=1,2,3,…,n)作为随机Markov过程的模态ri=r(i)，即系统中线路i发生故障，再利用式(6)计算出下一级线路故障的转移概率pij，由此可得出Markov转移概率矩阵π，至此，建立了基于事故链L的Markov过程[19]，最后算出电力系统最大时滞。算法的具体流程如图1所示。

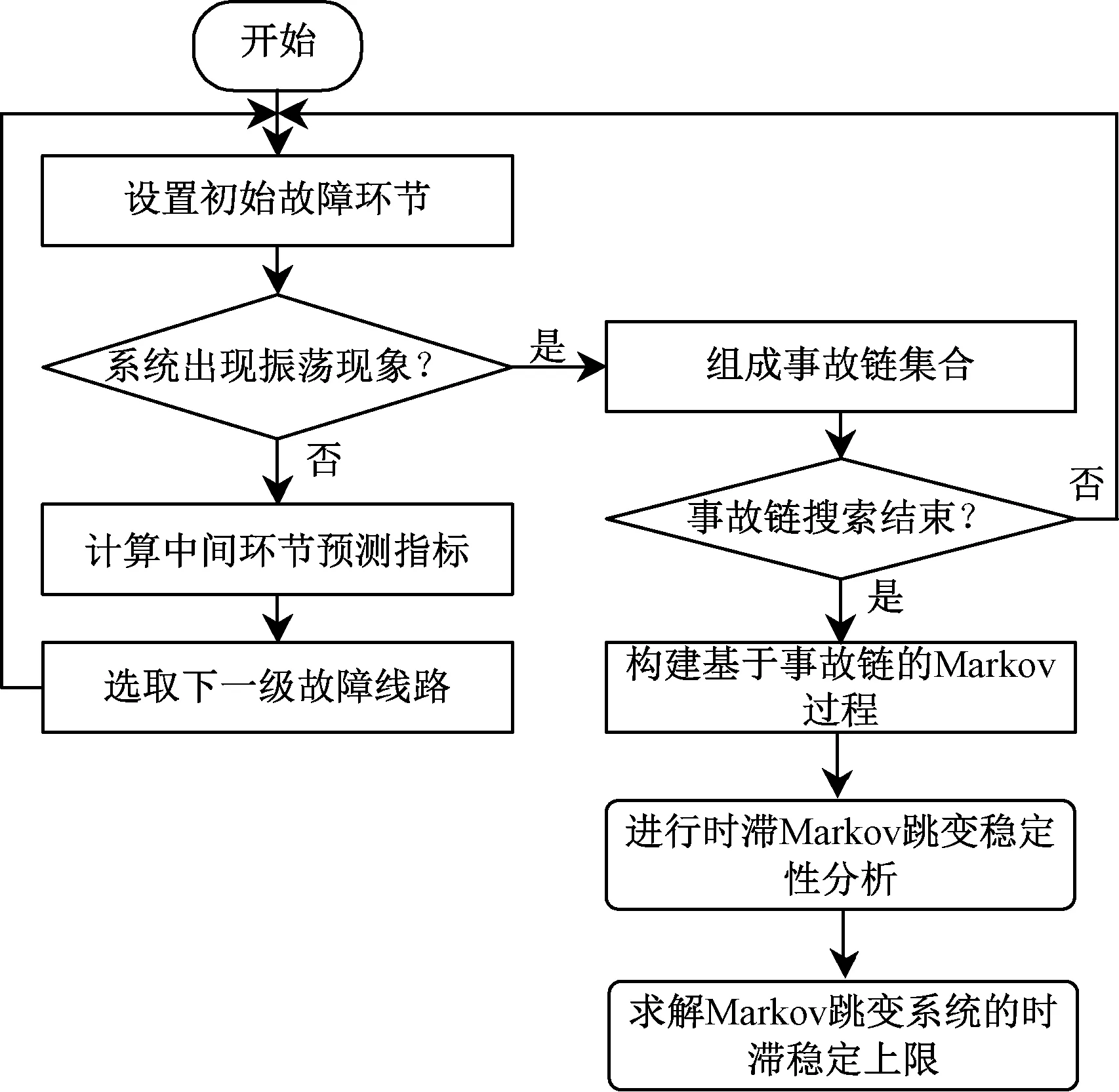
图1 时滞系统稳定性分析流程图

2 时滞Markov跳变系统的稳定性分析

2.1 时滞Markov电力系统模型

时滞Markov跳变系统的模型可以由下式表示：

(7)

时滞ht满足条件：

(8)

式中：x(t)∈Rn和z(t)∈Rn分别是系统的状态函数和输出函数；Ar(t)、Adr(t)、Br(t)、Bdr(t)为适当维数的已知矩阵；ht为系统时滞，rt=r(t)为时滞稳定上限；rt=r(t)为时滞的变化率。rt=r(t)为系统模态，取值于有限集合S={1,2,…,s}，为齐次的马尔科夫动态过程，矩阵π为马尔科夫的转移概率矩阵，其非对角线上的元素值可通过式(7)计算得到，对角线上的元素值为该行非对角线元素之和的相反数，具体的表达式为：

(9)

(10)

Ω2=[N+M,L-N, -L-M]

其中：

(11)

其中：

i={1,2，…，N}

本文中*表示相应的对称部分。

2.2 时滞稳定上限参数求解

(12)

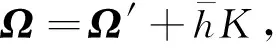
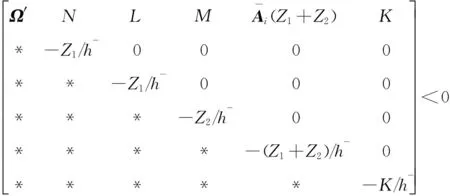
(13)

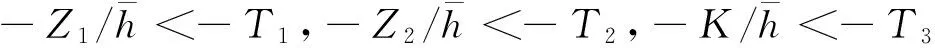
(14)

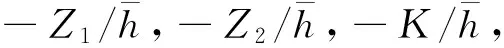
(15)

mind

s.t.(13) (14)

(16)

以式(13)和式(14)为约束，通过求解式(15)得到最小d，最终，令h=1/d，可以推导求出在连锁故障情况下，电力系统的时滞稳定上限。

3 算例分析

为验证本文所提方法的有效性和低保守性，以IEEE16机68节点的系统为例，采用时域仿真的方法，计算基于事故链和Markov过程的时滞电力系统的时滞稳定上限。如图2发电机模型采用的是6阶模型在仿真计算中，待求解模型动态方程的具体维数为10阶，通过定理1进行时滞稳定判断所需求解的待求变量数为21个。

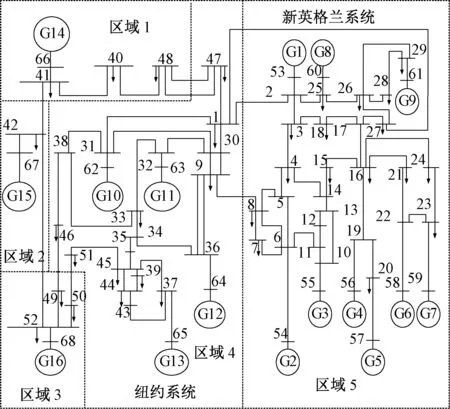
图2 16机68节点系统图

线路故障在电力系统故障中占大多数，并且考虑到区域间联络线的重要性，将事故链的触发环节定为联络线故障。根据本文第一节中的指标，预测事故链为：

L1={线路1-2 → 线路3-4 → 线路 2-3}

(17)

L2={线路46-49 → 线路32-33→

线路 31-38}

(18)

建立对应事故链L1和L2的Markov过程，系统模态rt=r(t)分别取值于有限集Sm={1,2,3},m=1,2，其转移概率矩阵为：

(19)

(20)

3.1 事故链L1

为了使本文所提方法的可行性和有效性得到验证，利用H2/H∞控制方法设计了IEEE 16机68节点系统的阻尼控制器如图2所示，详细参考文献[19]。将阻尼控制器分3个时段设置时滞，图3所示为发电机8～15与发电机1～16之间的相对功角差的动态响应曲线。

在事故发生的最终环节，发电机8～15与发电机1～16的相对功角差曲线阻尼比分别如表1和表2所示，该阻尼比是利用prony算法[20-21]得到的。

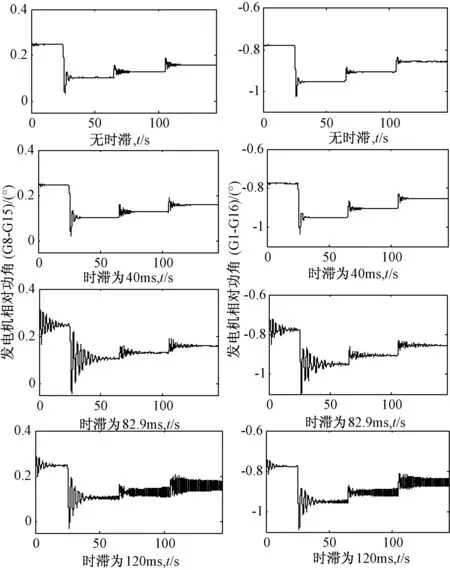
图3 系统不同时滞下发电机相对功角动态响应

由表1和表2可知，当系统发生连锁故障，且时滞达到82.9 ms时，功角差曲线的阻尼比分别减小到8.49%和9.62%，不满足控制要求。由此可得，通过结合事故链与马尔科夫动态过程来分析故障电力系统的时滞稳定性的方法是切实可行的。也是比较符合实际需求的。

表1 系统G8与G15功角差各时滞时间下的阻尼比

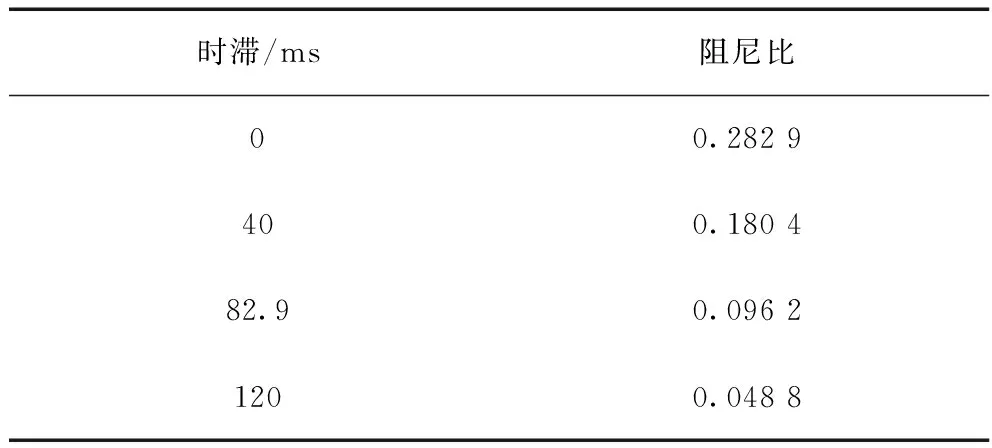
表2 系统G1与G16功角差各时滞时间下的阻尼比

3.2 事故链 L2

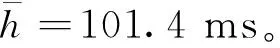
表3 系统G4与G13功角差各时滞时间下的阻尼比

由图4分析得出，当时滞的大小小于时滞稳定上限时，事故链的各个环节均可以在20 s内阻尼区间振荡；当时滞由0 ms增大到101.4 ms时，阻尼对电力系统频率振荡的负反馈作用降低，曲线发生摆动，当时滞增加至150 ms时，功角曲线摆动幅值增大，说明此时系统已经失稳。

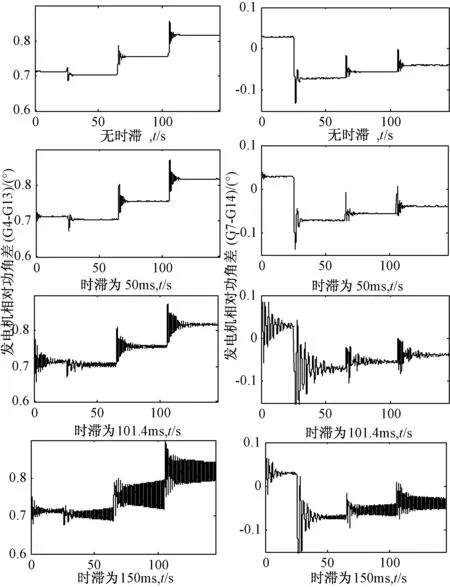
图4 系统不同时滞下发电机相对功角动态响应

由图4和表3、表4的分析可以得出，结合分析事故链与马尔科夫动态过程，合理地反映出故障时电力系统的时滞稳定性，有效地求得系统的时滞稳定上限。在事故链L1和事故链L2的分析过程中，通过定理1计算16机系统时滞稳定上限所用的计算时间分别为11.549 1 s(事故链L1)、10.294 6 s(事故链L2)。求解时滞稳定上限时所用计算平台的配置为：1) Windows 7 操作系统；2) Intel i5430 M处理器；3)1 GB DDR3内存；4)500G硬盘。

表4 系统G7与G14功角差各时滞时间下的阻尼比

3.3 保守性验证

表5 不同方法所能得到的时滞稳定上限

4 结论

本文提出一种基于事故链和Markov过程结合分析电力系统时滞稳定性的方法，得到如下结论：

(1)基于李雅普诺夫法并结合事故链与马尔科夫动态过程，能够计算得到时滞稳定性的上限，并且在一定程度上分析电力系统的时滞稳定性。

(2)如果将转移速率矩阵构建的自由权项引入到目标泛函的弱无穷小算子中，则能连续传递Markov过程转移速率矩阵信息。能够实时更新计算时滞稳定性的参数，提高结果的精确性。

(3)将Newton-Leibniz公式构造的自由权项引入目标泛函的弱无穷小算子中，在时域下将时滞分为两个子区间，这种运算方法大大降低了保守性。

参考文献：

[1]余晓丹，贾宏杰，王成山．时滞电力系统全特征谱追踪算法及其应用[J]．电力系统自动化，2012，36(24)：10-14．

[2]胡志坚，赵义术．计及广域测量系统时滞的互联电力系统鲁棒稳定控制[J]．中国电机工程学报，2010，30(19)：37-43．

[3]孙国强，屠越，孙永辉，等．时变时滞电力系统鲁棒稳定性的改进型判据[J]．电力系统自动化，2015，39(3)：59-62．

[4]尚蕊. 电力系统时滞稳定裕度求解方法[J]．电网技术，2007，31(2)：5-11．

[5]NEJAT O．A novel stability study on multiple time-delay systems (MTDS) using the root clustering paradigm[C]．Proceedings of the American Control Conference, 2004:5422-5427．

[6]NEJAT O．An exact method for the stability analysis of time- delayed linear time-invariant (LTI) systems[J]．IEEE Transactions on Automatic Control，2002，47(5)：793- 797．

[7]刘兆燕，江全元，徐立中，等．基于特征根聚类的电力系统时滞稳定域研究[J]．浙江大学学报(工学版)，2009，43(8)： 1473-1479．

[8]刘健辰，章兢，张红强，等．时滞系统稳定性分析与镇定：一种基于Finsler引理的统一观点[J]．控制理论与应用，2011， 28(11)：1577-1582．

[9]PARK P．A delay-dependent stability criterion for systems with uncertain time-invariant delays[J]．IEEE Transactions on Automatic Control，1999，44(4)：876-877．

[10]MOON Y S，PARK P，KWON W H，et al．Delay-dependent robust stabilization of uncertain state-delayed systems[J]．International Journal of Control，2004，74(14)：1447-1455．

[11]FRIDMAN E，SHAKED U．A descriptor system approach toH∞control of linear time-delay systems[J]．IEEE Transactions on Auto-matic Control，2002，47(2)：253-270．

[12]HE Yong， WANG Q，LIN C，et al．Delay-range-dependent stability for systems with time-varying delay[J]．Automatica，2007，43(2)：371-376．

[13]XU S，LAM J，MAO X．Delay-dependent control and filtering for uncertain Markovian jump systems with time-varying delays[J]．IEEE Transactions on Circuits and Systems I：Regular Papers，2007，54(9)：2070-2077．

[14]WANG J，LUO Y．Further improvement of delay-dependent stability for Markov jump systems with time-varying delay[C]．In： Proceedings of the 7th World Congress on Intelligent Control and Automation．Chongqing：IEEE Press，2008：6319-6324．

[15]ZHAO X D，ZENG Q S．Delay-dependent stability analysis for Markovian jump systems with interval time-varying-delays[J]．International Journal of Automation and Computing，2010，7(2)：224-229．

[16]吴文可，文福拴，薛禹胜，等．基于马尔可夫链的电力系统连锁故障预测[J]．电力系统自动化，2013，37(5)： 29-37．

[17]刘文颖，杨楠，张建立，等．计及恶劣天气因素的复杂电网连锁故障事故链模型[J]．中国电机工程学报，2010，30(19)：37-43．

[18]陈恩泽，刘涤尘，廖清芬，等．基于事故链的电网低频振荡及脆弱性分析[J]．中国电机工程学报，2011，31(28)：42-48．

[19]FENG X，LOPARO K A，JI Y，et al．Stochastic stability properties of jump linear systems[J]．IEEE Transactions on Automatic Control，1992，37(1)：38-53．

[20]BOYD S，EL GHAOUI L，FERON E，et al．Linear matrix inequalities in system and control theory[M]．Philadelphia，USA：SIAM，1994．

[21]TRUDNOWSKI D J，JOHNSON J M，HAUER J F．Making prony analysis more accurate using multiple signals[J]．IEEE Transactions on Power Systems，1999，14(1)：226-231．