提高大功率机电静压伺服机构动静态性能控制算法研究

刘 璐，张 朋，赵守军，史正强，张小红

0 引 言

机电静压伺服机构（Electro Hydrostatic Actuator，EHA，也称“电动静液伺服作动器”）作为功率电传作动系统的一种基本实现形式，保留了传统电液伺服机构重载能力强的优势，同时，具有节能、效率高、发热小、抗污染能力强等突出特点，是未来运载火箭推力矢量控制作动系统的主流技术方案[1～3]。

目前，国内外已有众多高校及科研院所进行EHA技术研究工作，文献[4]设计了一种双余度机电静压伺服机构，并讨论了两套电机泵状态下系统的余度管理方法，但该机构仅应用于低速场合，因此并未对其动态特性展开深入研究；文献[5]开展了10 kW机电静压伺服机构的动态特性研究，分析了其高动态实现的影响因素，采用“比例+陷波”的控制算法，带载状态下其频率特性在-3 dB时幅频的带宽为71.2 rad/s，-45°时相位滞后的带宽为18.5 rad/s，对于现役运载火箭的20 rad/s仍然存在差距。

为了进一步发掘机电静压伺服系统动态性能提升的潜力，在控制算法上进行更深入研究。本文提出了一种融合陷波器、非线性PID和前馈的控制方法，建立了数学模型，进行了仿真分析，制造了样机，完成了带载试验，表明采用该控制策略的机电静压伺服机构具有良好的动静态特性，可以满足未来大推力火箭发动机推力矢量控制需求。

1 系统设计

1.1 作动系统设计

机电静压作动系统是通过控制伺服电机泵的速度和正反转来完成活塞杆的精确位移输出，原理如图 1所示。控制器接收位置指令和反馈信号比较，经过驱动器控制电机泵的转速和转向，即流量控制。为防止气穴和空吸，设置波纹管式增压油箱和补油单向阀，高压安全阀设置系统的最高压力，旁通阀用于满足作动筒零位调整的需要。

机电静压作动器采用集成一体化设计，对外接口仅有安装支耳以及电连接器，电机泵、增压油箱、安全阀、单向阀、位移传感器等元件均集成在壳体上，消除了液压管路连接，减小控制体积以降低对作动器高动态性能影响，同时满足火箭发动机舱段狭小的安装空间要求[5]。样机结构设计如图2所示。

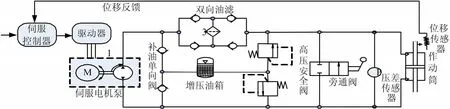
图1 机电静压伺服机构系统原理Fig.1 Simplified Schematics of the EHA

作为整个系统核心，伺服电机泵采用了“伺服电机+液压泵”一体化设计的理念，是“机械+电机+液压”的高度集成，具有结构紧凑、静音、高效率、无外泄漏等一系列突出优点，伺服电机浸油工作，其定子及转子由内部液压油润滑冷却。样机设计参数见表1。

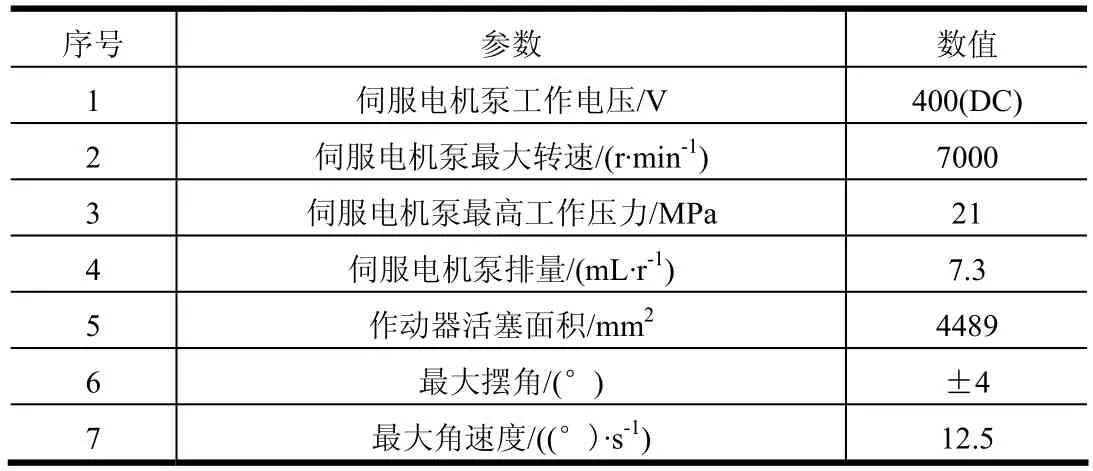
表1 试验样机基本设计参数表Tab.1 Main Parameters for the EHA

1.2 负载系统设计

火箭发动机喷管的结构复杂，各种非线性因素的耦合作用，使其体现出复杂的动力学特性。在对机电静压作动器进行动静态特性测试时，综合考虑负载的主要因素，包括：惯性负载、作动器安装刚度、摩擦负载等，其中惯性负载为主，建立负载模拟系统，带载静压作动器测试原理如图3所示。

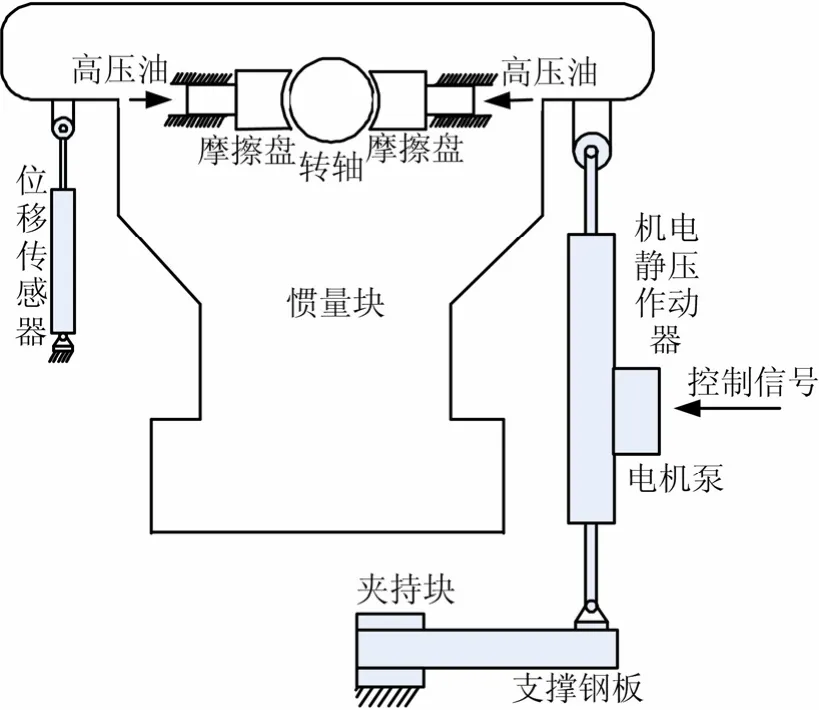
图3 机电静压作动器带载测试原理Fig.3 Simplified Schematics of the Loaded EHA Test System

2 系统建模及分析

2.1 系统建模

如图1所示，机电静压作动系统主要由控制器、伺服电机、柱塞泵、位移传感器和作动器组成。

在本文关注的中低频段可以将伺服电机速度闭环的近似等效为二阶环节，传递函数如下[5]：

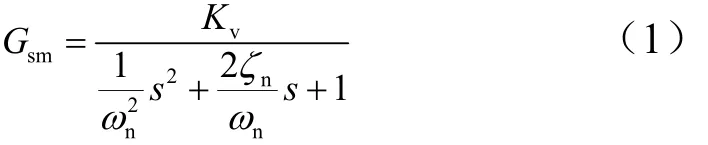
式中 Kv为电机速度增益；nω，nζ分别为伺服电机速度闭环的等效二阶环节自然频率和阻尼比。

定量泵高压腔流量连续性方程为

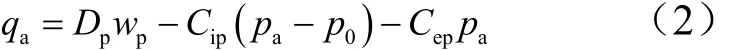
式中 wp为柱塞泵转速；Dp为柱塞泵排量；qa为柱塞泵高压腔油口流量；pa为柱塞泵高压腔油口压力；p0为系统低压压力；Cip为柱塞泵内泄漏系数；Cep为柱塞泵外泄漏系数。

进入作动器高压腔的流量连续性方程为

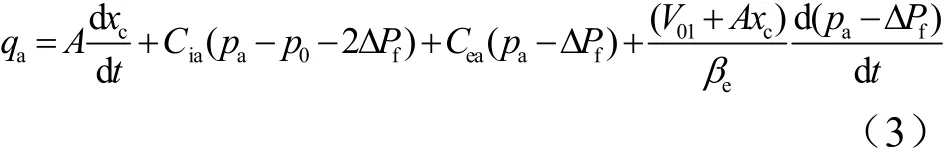
式中 A为作动器有效面积；xc为作动器活塞位移；Cia为作动器内泄漏系数；Cea为作动器外泄漏系数；βe为实测油液有效体积弹性模量；△Pf为系统中间液压元件压降；V01为作动器进油腔的初始容积。

作动器力平衡方程为

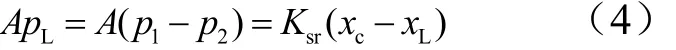
式中 p1为作动器进油腔油液压力；p2为作动器出油腔油液压力；Ksr为支撑刚度；xL为负载位移；pL为负载压力。

负载取主要的惯性部分，负载力平衡方程为

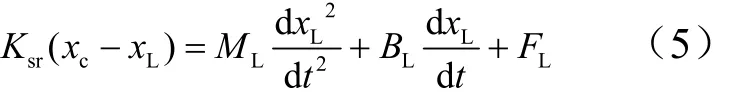
式中 ML为活塞及折算到其上的总质量；BL为负载粘性阻尼；FL为作用在负载上的外力。

不计静态负载影响，由式（5）可得作动器模型如图4所示。

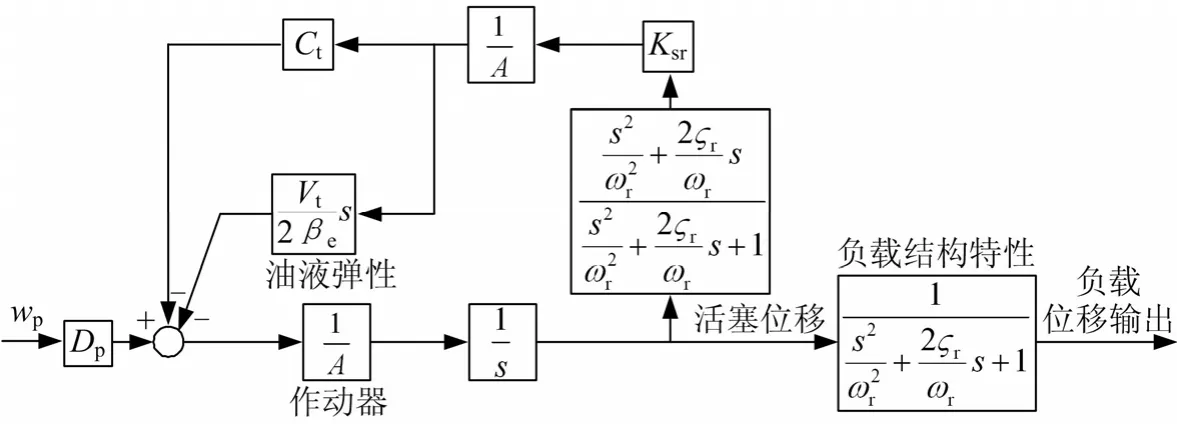
图4 作动器模型Fig.4 Block Diagram of the Actuator and Load

将泵控作动器闭环部分进一步简化，得到机电静 压伺服机构的位置闭环控制模型如图5所示

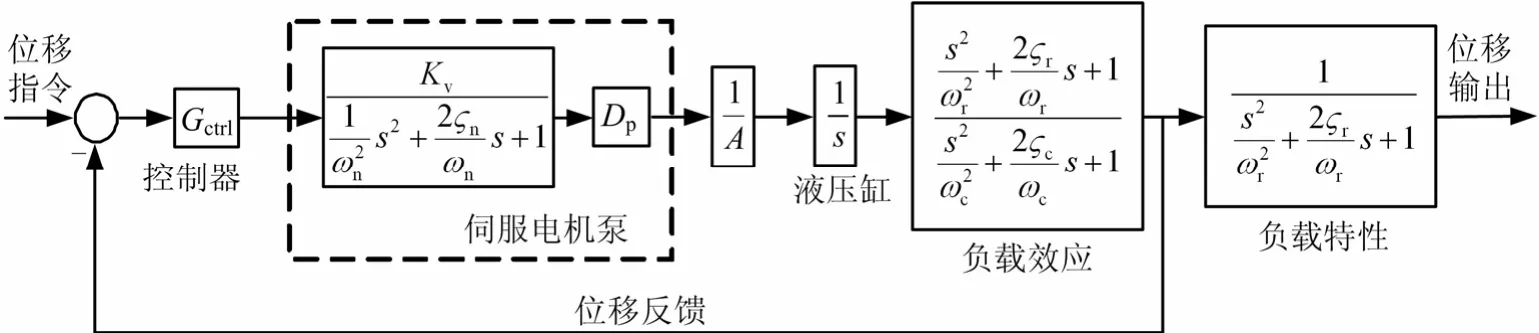
图5 机电静压伺服机构的位置闭环控制模型Fig.5 Block Diagram of an EHA

2.2 控制算法设计和分析

文献[5]采用“比例+陷波”这一基本控制律，控制器结构如图6所示[5]。

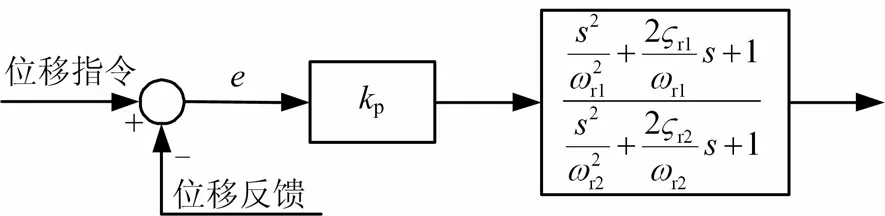
图6 “比例+陷波”控制器结构Fig.6 Schematics of Notch Filter and Proportional Controller

该算法结构简单、可靠性好，对于小惯性和小滞后系统较为适用，但EHA系统具有高度非线性、时变不确定性和纯滞后等特点，仅依靠恒定比例增益 kp无法兼顾动静态性能。因此，本文提出一种“陷波器＋非线性PID＋前馈”的控制算法，其结构如图7所示。

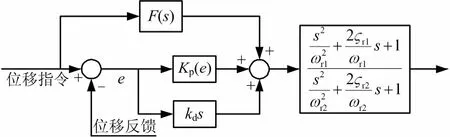
图7 控制器Gctrl结构框图Fig.7 Schematics of the Position Controller

针对常规PID难以协调快速性和稳定性之间的矛盾，采用一种非线性PID控制算法来提高系统的动态性能，算法如式（6）、（7）所示。

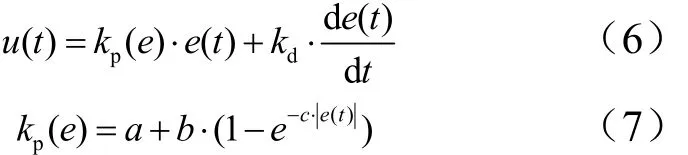
式中 a，b，c，kd为非负数；比例增益 kp(e)为系统偏差 e(t)的指数函数，当系统输出远离目标值时，kp(e)值较大，保证系统有较快的响应速度；当偏差e(t)逐渐趋向于0时，kp(e)随之减小，使系统在接近目标值时不至于有较大超调并提高系统稳定性。

然而，无论是传统PID控制还是非线性PID控制都依赖于系统产生偏差来输出控制量，并且为保证系统的稳定性，非线性PID所用的比例增益kp(e)在e(t)较小时取值很小，这就导致系统在跟随小幅值低频信号偏差值一直处于较小状态下控制效果较弱，静态特性不理想。针对该问题，在系统中引入前馈函数F(s)，在控制偏差为0的情况下输出指令，从而实现系统的快速响应。

设G(s)为作动器传递函数，当F(s)=1/G(s)时，系统的输出量与系统的输入量完全相同，具有理想的动静态性能。由2.1节可知，此时前馈函数为

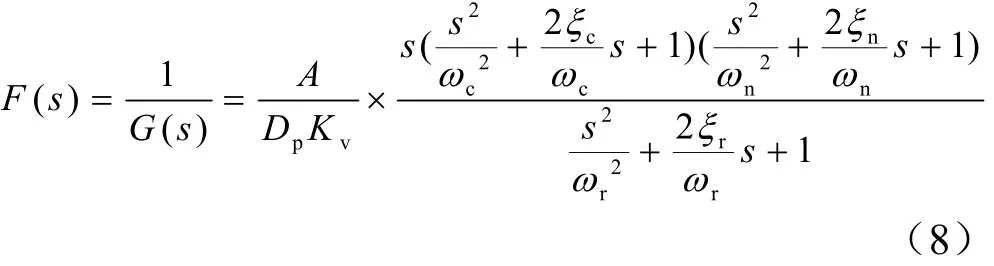
由于主要考虑提高低频段的特性以及工程实用性的需要，对F(s)进行降阶处理，得到简化后的前馈函数为

式中 kq为前馈系数，kq=A/DpKv。

3 仿真及试验研究

利用文献[5]采用的某型火箭发动机模拟负载台进行试验（转动惯量1000 kg·m2，零位力臂长876 mm，固有频率100 rad/s，阻尼比0.04）。控制器参数如表2所示（纯比例控制取：kp=1.6，此时系统开环增益ko=32.6）。

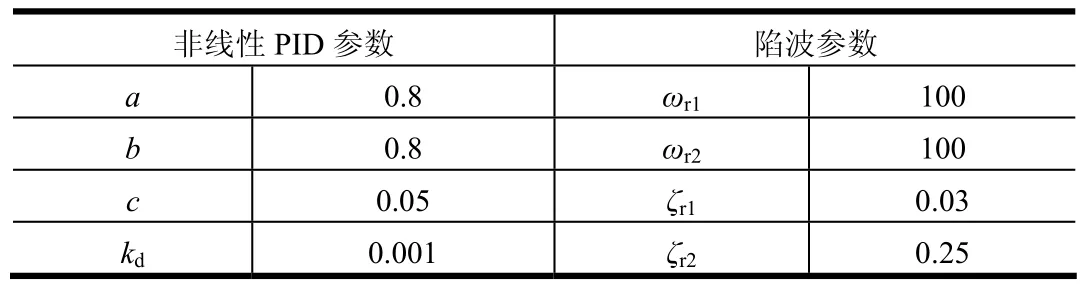
表2 控制器基本参数表Tab.2 Main Parameters for the Controller

3.1 正弦响应试验

输入幅值20 mm，频率1 Hz的正弦信号，试验样机仿真及实测曲线如图8所示。

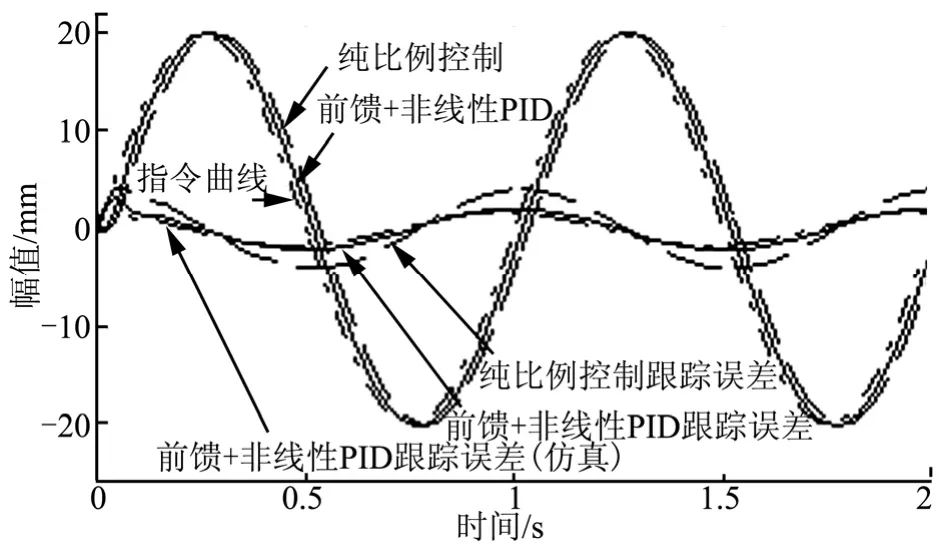
图8 正弦响应曲线Fig.8 Sinusoidal Position Tracking Curve

由图8可知，采用纯比例控制器的情况下，跟踪误差较大；采用非线性PID加前馈算法后，跟踪精度提高一倍，跟踪误差减小约50%。

3.2 频率特性试验

输入幅值0.1°（对应线位移1.5 mm）的正弦扫频信号，测得样机的频率响应曲线，同时给出采用“前馈+非线性PID”的仿真曲线，如图9所示。

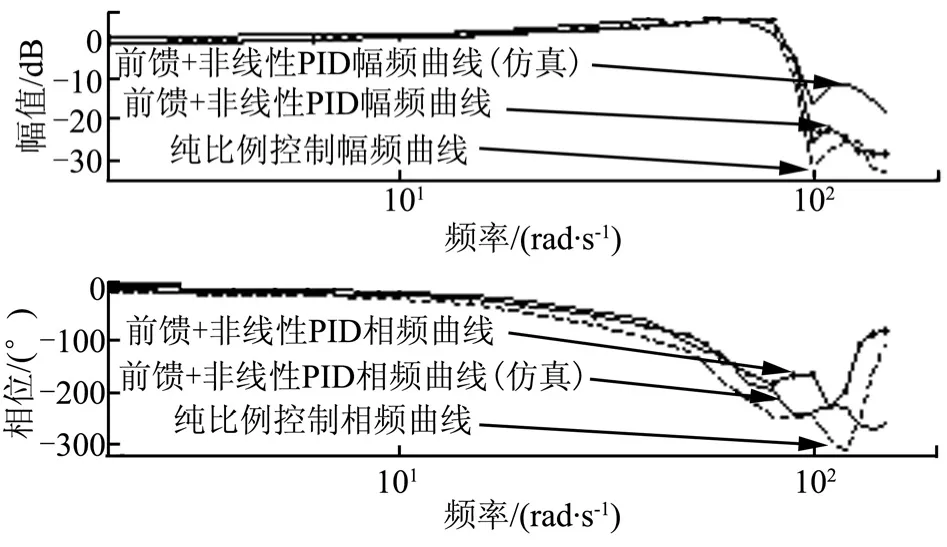
图9 频率特性曲线Fig.9 Frequency Response Curve

由图9可知，系统在纯比例控制下-3 dB幅频宽82.5 rad/s，-45°相频宽19 rad/s；在前馈+非线性PID控制器作用下，系统-3 dB幅频宽85.4 rad/s，-45°相频宽25 rad/s，且在高频段谐振峰值并未增大，试验结果与仿真曲线基本吻合，表明采用前馈+非线性PID的控制策略可有效提高系统的动静态性能。

4 结 论

本文针对 EHA系统难以兼顾高动态响应和高精度控制的问题，提出了融合陷波器、非线性PID和前馈的控制方法来提高系统的动静态性能，通过理论分析以及建立EHA系统模型确定了比例增益kp相对于系统偏差e(t)的函数并推导出前馈函数F(s)；进行Matlab仿真和试验研究对算法验证，结果表明“陷波器＋非线性 PID＋前馈”控制器既克服了系统对低频小幅值跟踪精度较差的问题同时也提高了响应速度，显著改善了系统相位滞后较严重的问题，满足未来运载火箭摇摆发动机推力矢量控制的要求。