一种强跟踪UKF及其在GPS/SINS深组合导航中的应用

叶 晨，崔双喜

0 引 言

基于GPS/SINS的深组合导航系统与松/紧组合导航不同，信息融合程度更深。其中导航滤波器的状态更新可由接收机通道采样值提供，滤波输出值校正码产生器与载波的控制值，使得载波相位跟踪带宽更宽，抗干扰性能更强。然而在动态高、干扰过强等恶劣环境下，接收机相关器输出值仍具有较强的非线性[1]。

针对这种非线性问题，一般有两种方法[2～3]：a）将非线性函数进行线性化处理，只保留低阶项信息，经典方法是扩展卡尔曼滤波（Extended Kalman Filter，EKF）；b）使用采样的方法近似非线性分布，该方法可以较好地避免EKF存在的部分问题，如无损卡尔曼滤波（Unscented Kalman Filter, UKF）算法[4～5]。然而，状态突变、模型不准确均可能引起系统的跟踪能力变差、鲁棒性能降低，针对此难题，根据新息向量的正交性原理，有学者提出了强跟踪滤波器的思想，并运用在EKF的改进中，可有效处理模型不确定性问题，提高系统的动态跟踪性能[6]。

系统状态异常时，标准UKF无法自适应调节，将导致组合导航滤波结果精度降低。本文立足于基本UKF算法框架，并结合强跟踪滤波的基本理论，可使状态预测估计协方差矩阵在线自适应修改调整，建立一种多重渐消因子的强跟踪UKF跟踪器，并将此算法运用到发射惯性系下 GPS/SINS深组合导航仿真研究中。结果表明，当状态系统、量测系统遭到干扰时，该算法相对于标准UKF估计精度更高、适应性能更强。

1 UKF算法

UKF和标准KF都属于线性最小方差估计滤波算法。但与标准KF不同的是，UKF算法根据被估计量和量测量的协方差阵来确定最佳增益阵，协方差阵又根据复现的 1倍σ样本点来计算，这些样本点则根据系统方程和量测方程来确定且并未对系统方程和量测方程提出任何附加条件。因此算法既适用于线性对象，也适用于非线性对象[7]。

本文考虑如下离散时间非线性系统：

式中 Xk， Zk分别为k时刻系统的状态向量、观测向量，Xk∈Rn,Zk∈Rm； Fk为线性状态转移矩阵； h(·)为系统非线性量测函数； wk， vk为零均值高斯白噪声序列，向量互不相关，统计特性满足如下条件：

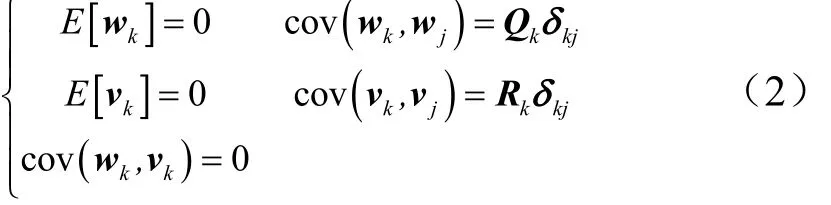
式中kQ为非负定矩阵；kR为正定矩阵；kjδ为Kronecker-δ函数。

标准UKF算法的具体流程[4]如下：

a）初始化。

假定系统的初始状态为0X高斯分布的随机向量状态初始化条件：

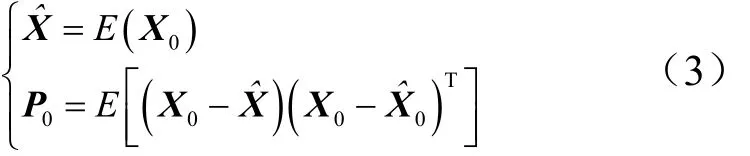
式中 P为协方差。

计算采样点：对于 n ≥1，在仅考虑输入变量的均值Xˆ和协方差P的情况下，将Xˆ和P由Sigma点近似，由 Sigma点对称采样策略的采样函数，可得到如下2 n +1个采样点：

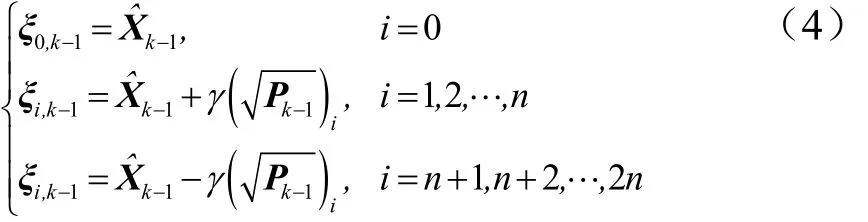
式中 ξ为状态量参数；()i为矩阵Pk−1均方根的第i列；nγλ=+，参数λ的确定为

式中 参数α是很小的正数，可取 1 0−4≤α≤1；κ=3− n ；确定采样点的权值：

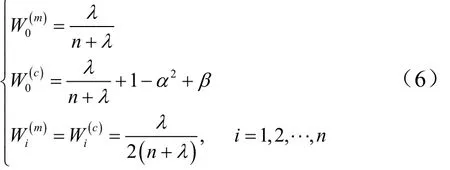
式中 β取值与X的分布有关，对于正态分布，2β=为最优值。

b）预测方程。

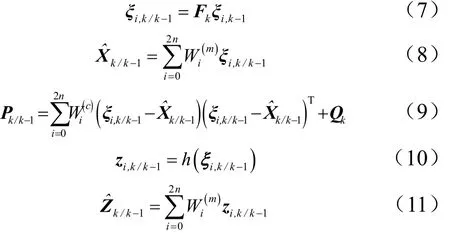
c）更新方程。

2 强跟踪UKF算法

2.1 强跟踪滤波器

强跟踪滤波器[6～8]（Strong Tracking Filter，STF）与普通的滤波器相比，状态突变时的跟踪能力更强，模型不确定性时鲁棒性能更高。其主要思想是：实时调节修正滤波K矩阵，强制残差向量彼此保持正交，这样可使滤波器依然能够跟踪在系统模型不确定时的系统状态变化，从而改善了UKF鲁棒性差和滤波发散的问题。渐消因子λk根据系统可实时变化，并影响预测协方差矩阵Pk/k−1的构造，从而实时修正增益Kk。记导航滤波器输出的残差序列 εk= Z ˆk− Zˆk/k−1，则强跟踪器应满足如下条件：

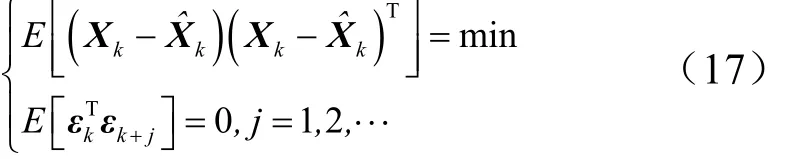
式中表征滤波器可以实现最优估计的性能要求；保证残差序列向量在不同时刻保持正交，同时具有类似白噪声的性质，将残差序列的不相关性作为衡量滤波性能是否优良的标志。

2.2 渐消因子的引入

经过理论基础的支持，本系统采用多重次优渐消因子，分别对不同的数据进行渐消，进一步提高滤波器的跟踪能力。对一步预测状态误差协方差阵式（7）作如下调整[9～11]：

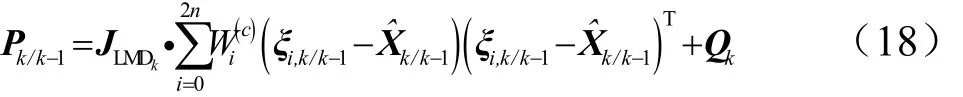
式中

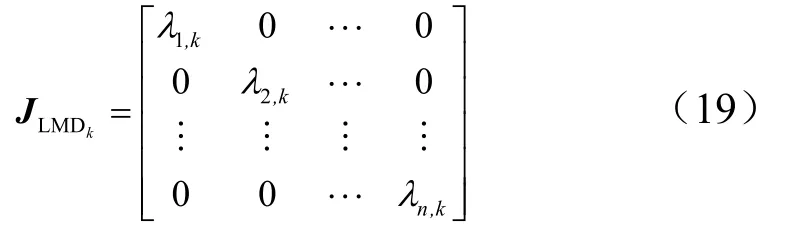
称为渐消矩阵。

为n个渐消因子。由系统的先验知识可大致确定：

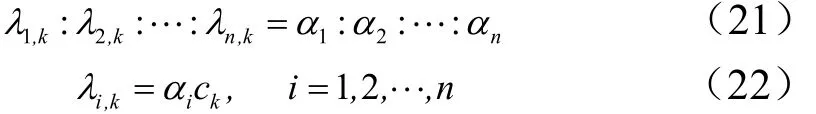
式中 α为可提前确定的常数，αi≥1；ck为待定因子，则多重渐消次优因子的一步算法如下：

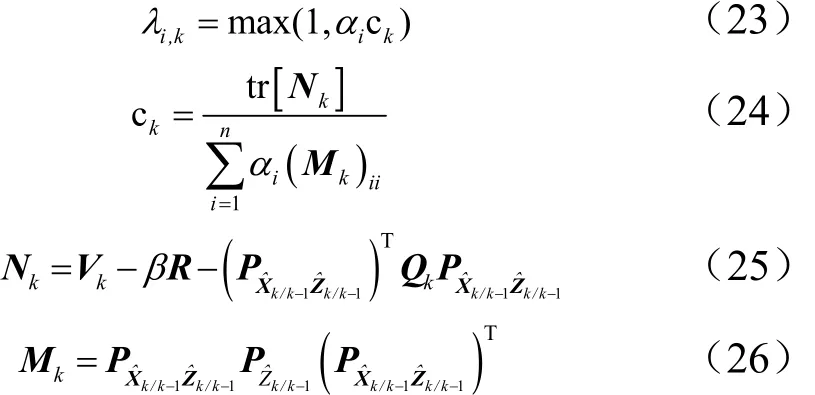
式中 β为弱化因子；1β≥，引入弱化因子可以使状态估计更加平滑，它的取值可以通过经验来确定；kV为实际输出残差序列的协方差阵，可有下式估算：

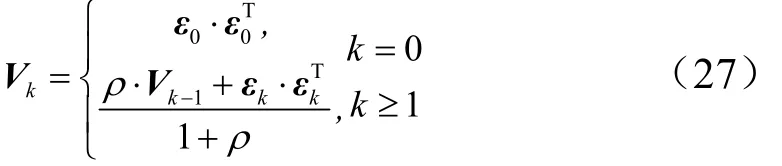
式中 ρ为遗忘因子，01ρ＜≤，一般取0.95。

3 深组合导航模型建立

GPS/SINS深组合导航系统的重要特征是GPS与SINS信息融合程度更深，涉及到惯导辅助GPS接收机内部跟踪环路等深层次信息交互。

深组合导航系统中，首先采集 SINS输出信息与GPS接收机输出信息并进行处理，建立对SINS位置误差、速度误差及姿态误差等状态变量的系统状态方程和量测方程，经过STUKF滤波器的自适应估计，输出状态误差进行校正系统状态，同时使用惯性信息辅助GPS接收机跟踪环路，可实现两个系统在观测过程中的相互辅助。这种系统模式可降低载波环跟踪环路噪声误差、抑制部分GPS跟踪环路动态应力误差，加强系统抗干扰性能和动态跟踪能力，本系统中，采用基于伪距、伪距率的紧组合强跟踪UKF滤波器，直接采用 GPS接收机的原始测量值（伪距、伪距率），不会引入GPS接收机导航解算带来的误差[12，13]。

3.1 深组合系统状态方程

3.1.1 SINS的误差状态方程

SINS的误差状态方程为

式中 φx，φy，φz为姿态失准角；δVx，δVy，δVz为发射惯性系坐标系下三轴方向的速度误差；δX，δY，δZ为发射惯性系三轴方向的位置误差；εx，εy，εz和∇x，∇y，∇z为弹体坐标系下陀螺仪常值漂移和加速度计常值偏置。

系统状态转移矩阵 F ( t )、噪声驱动矩阵 G ( t)和噪声向量 W ( t)的计算公式见参考文献[14]。

3.1.2 GPS的误差状态方程

在深组合系统中，可认为距离率误差rulΔ等效时钟频率误差，距离误差ulΔ等效时钟误差，作为GPS接收机的误差状态量，其状态方程为

式中，ruT为时钟漂移的相关时间；uw为GPS时钟误差白噪声，ruw为 GPS时钟频率误差白噪声。

3.2 系统观测方程

本系统中，发射惯性系弹道导弹GPS/SINS深组合导航系统分为伪距观测方程和伪距率观测方程两个部分，其可表示如下：

式中 ρ为某一时刻导弹发射惯性系位置的真值为[X YZ ]T时，设该时刻导弹距离GPS卫星理想的距离；ρi为SINS计算所得载体与第i颗卫星间的伪距；ρg为GPS接收机得到位置与第i颗卫星间的伪距为

式中ulδ为GPS的时钟误差引起的距离误差；vρ为伪距量测噪声。ρ与iρ可由下式计算得出：

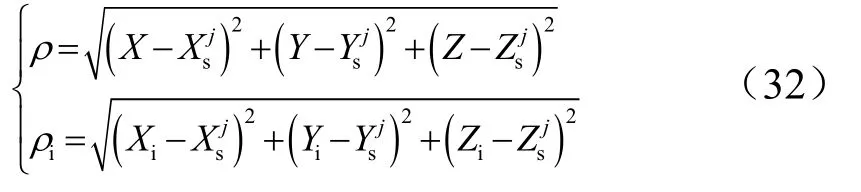
式中为 SINS解算得到的导弹在发射惯性系下的位置；为第j颗卫星转换到发射惯性系下的位置坐标。设[δ X δY δZ ]T是SINS计算位置与真实位置的距离误差，可知：

故，伪距率差非线性观测方程为

同样可推导出伪距率差非线性观测方程为

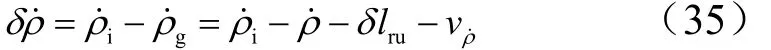
式中 ρ˙为此刻真实的伪距率；rulδ为由GPS时钟引起的距离误差；vρ˙为测量噪声。具体推导过程见文献[14]。应注意，由于采用非线性UKF滤波方法，系统观测方程无需线性化。

4 仿真校验

将提出的强跟踪UKF算法应用于GPS/SINS深组合导航进行仿真校验，并且与标准UKF算法进行比较。

4.1 仿真条件

以仿真某弹道导弹轨迹为背景，设置仿真条件为：初始俯仰角为 90°，初始滚转角和偏航角均为 0°；初始位置为：纬度32.08°，经度118.7°，高度为0 m；发射惯性系坐标系初始速度前向为394.891 7 m/s（地球自转速度），天向和侧向均为 0 m/s；发射方位角为 90°；陀螺零偏为10 (°)/h，白噪声为1 (°)/h；加速度计零偏为1 mg，白噪声为0.5 mg；收星数m=4。GPS采样周期1 s，INS采样周期0.005 s，滤波周期1 s，仿真时间360 s。在200～210 s时间段内，GPS伪距加入均值为0 m/s，标准差为100 m的白噪声；GPS伪距率加入均值为0 m/s，标准差为1 m/s的白噪声。

4.2 仿真结果与分析

图1表示的是弹道导弹轨迹，图2是标准UKF定位误差曲线，图 3是强跟踪 UKF定位误差曲线。由图2与图3相比较可知，在系统受到强力干扰的情况下，强跟踪UKF算法的优势凸显出来，相比标准UKF算法，误差波动较小，组合导航定位精度有大幅提升，具有更优越的抗干扰能力和鲁棒性。

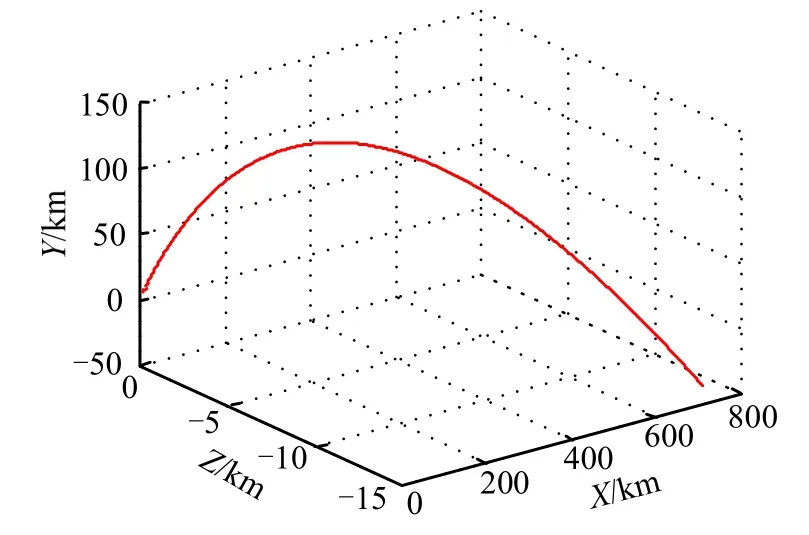
图1 发射点惯性系下的弹道导弹轨迹Fig.1 Trajectory of Ballistic Missile

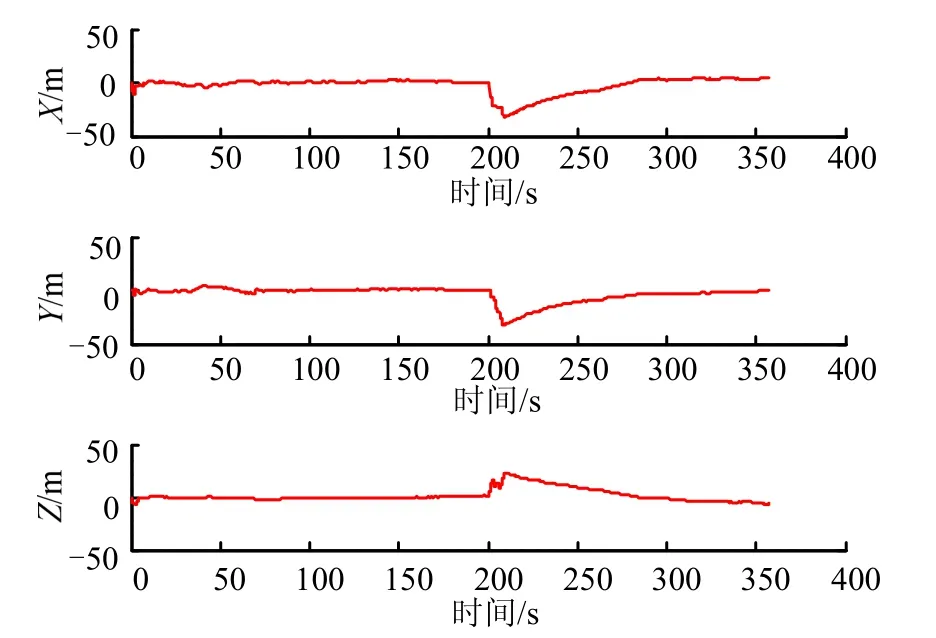
图2 标准UKF定位误差曲线Fig.2 Positioning Error of Standard UKF

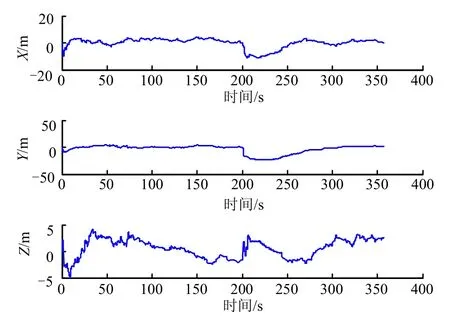
图3 强跟踪UKF定位误差曲线Fig.3 Positioning Error of Strong Tracking UKF

5 结 论

本文提出了一种强跟踪UKF算法，该算法通过引入多重渐消因子，使得滤波器具有更多的系统先验知识，增加了系统的鲁棒性能，并将该算法应用于发射惯性系下的GPS/SINS深组合导航中。仿真结果表明，该算法能为组合导航提供较高的导航精度，证明了该算法的有效性。