有控再入飞行器适时引爆战斗部方法研究

庞桂凤，刘 赛，张 琦，李 磊

0 引 言

有控再入飞行器是指安装有制导控制系统再入大气层飞行的航天飞行器，该型飞行器具有飞行速度高、可实时提供飞行速度和高度信息等特点，可携带整体式或子母式战斗部。

为发挥子母战斗部的最佳毁伤效能，必须将子弹着靶速度、子弹群散布精度和子弹群分布半径控制在一定范围内。而子弹着靶速度、子弹群散布精度和子弹群分布半径由战斗部引爆点参数决定，由于飞行干扰和各种偏差的存在，使得飞行器实际飞行弹道偏离理论弹道，实际引爆点参数偏离理论引爆点参数，引起子弹着靶速度、子弹群散布精度和分布半径不理想，造成战斗部的毁伤效果不理想，甚至不满足设计要求[1]。

为了获得战斗部最佳毁伤效能，本文创新性地提出了一种利用制导控制系统实时信息适时发出引爆信号的方法，该方法在满足子弹着靶速度的前提下，对子弹群散布精度和分布半径也进行了优化设计，战斗部的毁伤效能整体最优。

1 研究思路

本文研究思路如下：

a）通过子弹地面毁伤效应试验，获得子弹的最佳着靶速度cv的范围；

b）通过毁伤效果仿真计算，获得子弹群的散布精度CEP和最佳分布半径cr范围；

c）初步计算确定战斗部引爆点高度0ph 、引爆点速度0pv 和子弹初始飞散速度0v范围；

d）采用Monte-Carlo模拟打靶方法进行弹道仿真，计算不同引爆点参数条件下子弹群的散布精度和分布半径，以及子弹着靶速度；

e）采用回归分析方法对输出参数进行拟合，确定飞行器速度tv、子弹着靶速度cv、子弹群分布半径cr和子弹散布精度CEP的预测函数。

f）根据子弹类型和工程经验，确定优化的目标函数（如子弹着靶速度cv）和约束条件；

g）编制优化计算程序，计算求得优化后的引爆点参数及对应的子弹着靶速度、散布精度和分布半径；

h）为减化飞行器控制系统或引控系统软件，提高实时求解速度，给出引爆点预测速度ptv=和实时确定的引爆点高度ph的简单数据式；

i）将适时引爆函数写入飞行器控制系统或引控系统软件内。

本文中数学符号的下标t、p0、p、c分别为飞行中某时刻、“射前装订”引爆战斗部时刻、实时计算引爆战斗部时刻、子弹落地（着靶）时刻。

2 飞行器（子弹）飞行动力模型

本文假设地球模型为圆球、地球表面为平面，同时，忽略战斗部装药引爆时对飞行器和子弹位置的影响，建立的飞行动力坐标系和飞行动力模型如下：

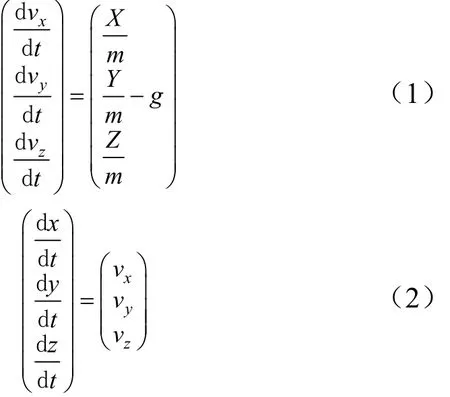
式中xv，yv，zv分别为飞行器（子弹）速度在地面坐标系Ox，Oy，Oz轴上的分量；m为飞行器（子弹）的质量；g为重力加速度；X，Y，Z分别为飞行器（子弹）气动力在地面坐标系Ox，Oy，Oz轴上的分量；x，y，z分别为飞行器（子弹）质心在地面坐标系的坐标。

限于篇幅，本文只给出基本方程，其它动力学方程和辅助方程详见文献[2]和文献[3]。因cv、cr、ph、pv和0v的计算方法成熟，并且已广泛应用于工程，本文不再赘述，重点研究预测函数、优化方法及实现方法。

3 算 例

已知某子弹着靶速度的最优值为（650±50）m/s，子弹抛撒半径为（113±27） m，子弹散布精度要求小于15 m。根据式（1）、式（2）及相关动力学方程，不考虑各种偏差因素，通过仿真计算初步确定引爆点高度ph范围为（3500±1000） m，引爆点速度pv 为（900±100） m/s，子弹初始飞散速度0v为45 m/s。

若将引爆高度0ph “射前装订”值设为 3500 m，在考虑引爆点参数（包括飞行器高度、飞行器速度、当地弹道倾角、子弹初始飞散速度和子弹初始总攻角等）偏差、大气偏差、风速偏差和阻力系数偏差等影响时，子弹着靶速度为650±100 m/s，不满足子弹着靶速度的最优值要求650±50 m/s。

为了分析、剔除各种偏差对飞行器速度、子弹着靶速度、子弹抛撒半径和子弹散布的影响，采用Monte-Carlo方法对飞行器弹道和子弹飞行弹道进行了仿真计算，并对这些数据进行了统计，得到预测模型。

3.1 飞行器速度预测模型

仿真结果表明，在飞行末段，飞行器的飞行速度随高度呈线性变化，利用回归分析方法，拟合出如下预测模型：

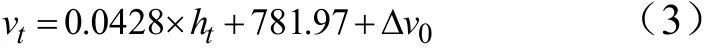
式中tv为某时刻飞行器飞行速度；th为某时刻飞行器飞行高度；0vΔ是实测（实际）速度与标称速度的偏差。

3.2 子弹着靶速度预测模型

子弹的飞行过程非常复杂，与子弹气动外形、气动参数、大气参数、初始飞散速度以及飞行姿态等相关，为减少优化函数、提高求解速度，本文对子弹的落点参数进行了统计分析，然后利用回归分析方法确定子弹着靶速度与引爆高度和速度的数学关系式：

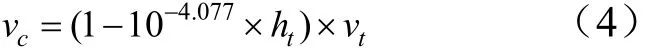
式中cv为子弹着靶速度。

为了验证子弹着靶速度模型的正确性，进行了大量计算，战斗部引爆高度与子弹着靶速度关系如图 1所示。由图1可知，预测值和模拟打靶值最大偏差不超过10 m/s，并且引爆高度在3000～4000 m时精度更高。

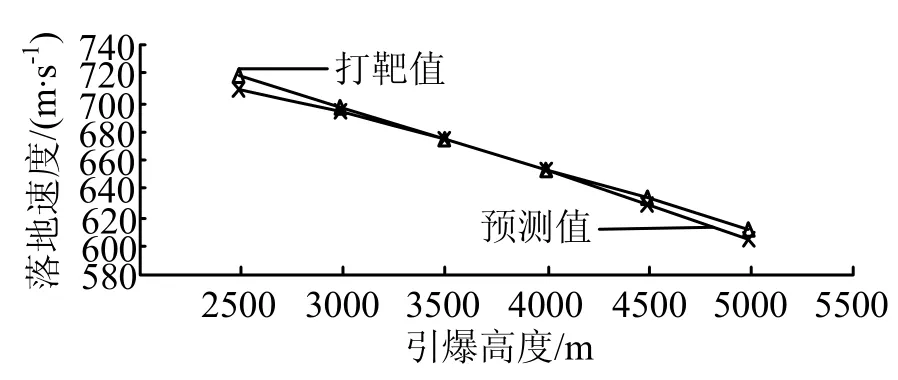
图1 战斗部引爆高度与子弹着靶速度关系Fig.1 Relationship Between Warhead Initiation Height and Projectile Target Velocity

3.3 子弹群分布半径预测模型

采用上述方法，也可以确定子弹群分布半径与引爆高度和速度的数学关系：

式中0ν为子弹初始飞散速度，本文取45 m/s；ch为子弹着靶点高程。

为了验证子弹群分布半径预测模型的正确性，也进行了大量数据验证，战斗部引爆高度与子弹群分布半径关系如图2所示。由图2可知，在2500～4000 m时二者偏差在5 m以内。

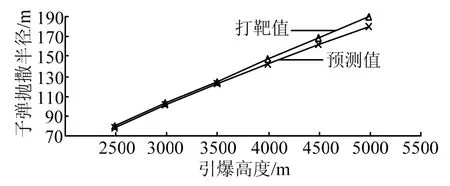
图2 引爆高度与子弹群抛撒半径关系Fig.2 Relationship Between Detonation Height and Distribution Radius of Bullet Cluster

3.4 子弹散布精度预测模型

与子弹着靶速度的预测方法相同，子弹散布精度的表达式为

战斗部引爆高度与子弹散布精度关系如图3所示。由图3可知，引爆高度在2500～4000 m范围内偏差小于1 m，精度较高，4000～5000 m时精度下降，最大偏差约为2.6 m。

图3 子弹的引爆高度与散布精度曲线Fig.3 Scattering Height and Precision Curve of Bullets

3.5 适时引爆的优化及模型

依据给定条件，确定一个目标函数和5个约束条件，将式（4）、式（5）、式（6）代入式（7），采用增广Lagrange乘子法[4～9]编制程序对th和tv进行寻优，优化结果即为ph和pv。

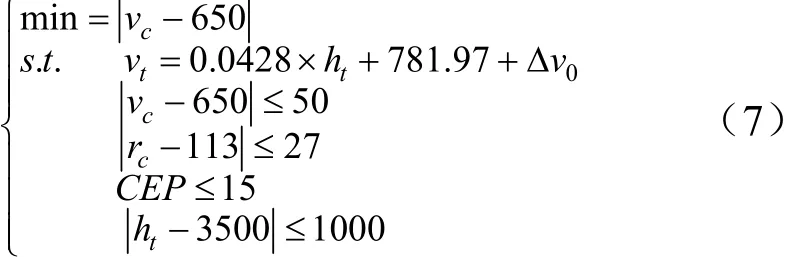
经过优化计算结果如表1所示，由表1可知，子弹着靶速度cv在623.77 m/s和700.0 m/s之间，相对650 m/s偏差范围是-26.23～50.0 m/s，实现了子弹着靶速度偏差小于50 m/s的控制目标。

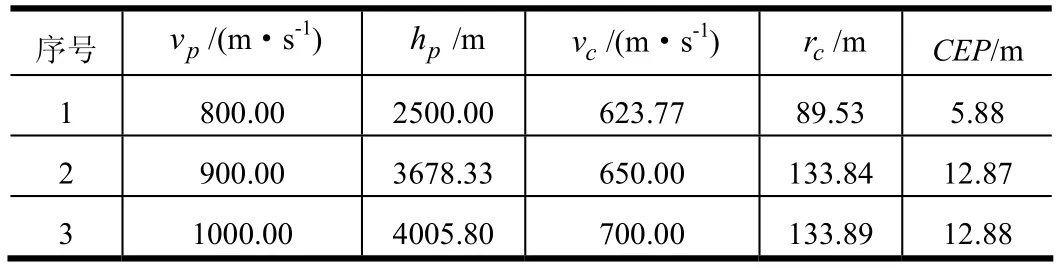
表1 优化结果Tab.1 Optimization Result

为减化飞行器控制系统或引控系统软件，提高实时求解速度，统计pv和ph，得出“射前装订”引爆点预测速度和适时引爆函数：

式中tpv=为射前装订引爆点（高度）处飞行器速度，可根据式（3）实时计算得到；ph为实时确定的引爆高度。

4 适时引爆战斗部的实现

假设飞行器“射前装订”的引爆高度ph为2500 m，按算例3方法得到类似式（8）的适时引爆函数，并将该适时引爆函数写入控制系统或引控系统软件。

在飞行末段飞行器实时采集的速度为1v，2v，v3，…，对应的高度为 h1， h2， h3，…，通过解算求到可以求得（9）中的c0和c1，实时得到飞行器的飞行速度与飞行高度模型：

将0ph =2500 m代入式（9），就确定了“射前装订”引爆点飞行器的“真实”速度tv，再将tv代入适时引爆函数，通过判定、计算、输出新的实时确定的引爆高度ph。

5 结 论

本文提出在不改变子弹装药量的前提下，通过改进飞行器控制系统软件提高战斗部毁伤效果的方法可行，实现简便。

因整体式战斗部相对子母式战斗部毁伤约束条件一般更少，计算模型一般更为简单，可在子母式战斗部研究成果基础上进行相应的简化处理得到。因此，这种方法不仅适用于子母式战斗部，也适用于对飞行器速度有较高要求的整体式战斗部。