非Chetaev型非完整系统Tzénoff方程Mei对称性的共形不变性与守恒量

郑世旺

(商丘师范学院 电子电气工程学院，河南 商丘 476000)

0 引 言

动力学系统对称性的研究是为了寻找其中的守恒量，动力学系统中存在的守恒量能揭示其中的守恒规律，进入21世纪以来,对称性与守恒量的研究得到了蓬勃发展[1-11].2000年梅凤翔教授提出一种新的对称性理论[2]，时称形式不变性，后被称之为Mei对称性，Mei对称性提出后，一种新的守恒量被发现，被人们称之为Mei守恒量，现在，Mei对称性及其守恒量的研究已涉及到多种动力学系统[2].共形不变性的研究起源于俄罗斯学者Galiullin等人[12]，并于2008年以后在我国得到发展，现已扩展到多个领域[13-18].在分析力学中有多种动力学方程，这些动力学方程虽然形式各异，动力学函数也不尽相同，但本质上是等价的、相通的.Tzénoff方程作为动力学方程的一种，虽然其动力学函数构造起来较为困难，但动力学方程的结构形式却较为简捷，目前，Tzénoff方程对称性与守恒量的研究也取得了不少成绩[19-24]，但其共形不变性的研究才刚起步[25-26].关于非完整动力学系统的研究基本上是以Chetaev型为前提，而实际上，非Chetaev型非完整系统则更为普遍.本文研究了非Chetaev型非完整约束系统Tzénoff方程的Mei对称性共形不变性及其守恒量.定义了系统共形不变性的概念并给出判据方程，探究该系统Mei对称性共形不变性在满足什么条件下才产生守恒量，并给出守恒量的函数式和导出这种守恒量的条件方程，最后展示一个研究例证.

1 非Chetaev型非完整约束系统的Tzénoff方程

设由n个广义坐标qs(s=1，…，n)来确定动力学系统的位形，它的运动受有g个双面理想非Chetaev型非完整约束

(1)

约束加在虚位移上的限制为

(2)

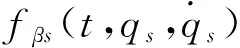
(3)

(4)

(5)

(5)式中

(6)

可由方程(4)求出广义加速度

(7)

由(7)式可得到

(8)

2 非Chetaev型非完整约束系统Tzénoff方程Mei对称性的共形不变性

把时间和坐标做无限小变换

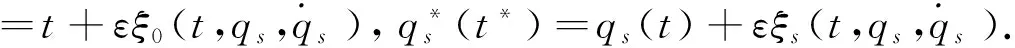
(9)

其中ξ0，ξs为无限小变换生成元，ε是一无限小参数.于是有

(10)

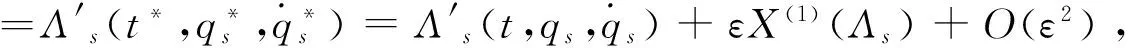
(11)

(12)

其中

非完整约束(1)在(9)式变换下的不变性表示为约束限制方程

(13)

因为用变换后的动力学函数替代原动力学函数，动力学方程的形式仍保持不变的一种对称性称为Mei对称性[2]，故可利用(10)-(12)式与方程(5)、(1)之间的关系得到

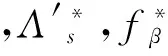
(14)

或

(15)

且约束限制方程(13)成立，则这种不变性称之为非Chetaev型非完整约束系统Tzénoff方程的Mei对称性.方程(15)即为系统Mei对称性的判定方程.

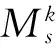
(16)

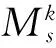
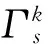
(17)

证明 设非Chetaev型非完整约束Tzénoff方程(5)是Mei对称性的，则方程(15)成立，(17)式变为

(18)

反之，若Tzénoff方程(5)成立共形不变性，(16)式和(17)式二者相减得

(19)

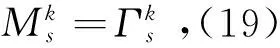
3 非Chetaev型非完整约束系统Tzénoff方程Mei对称性共形不变性所导出的守恒量

非Chetaev型非完整约束Tzénoff方程Mei对称性的共形不变性在满足一定条件下可导出相应的守恒量.

定理针对非Chetaev型非完整约束系统Tzénoff方程Mei对称性共形不变性的生成元ξ0，ξs，若能找到函数G满足如下结构方程

(20)

则Tzénoff方程Mei对称的共形不变性将直接产生一种守恒量

(21)

(20)式中

证明 对(21)式求导并利用非Chetaev型非完整约束系统Tzénoff方程Mei对称性及其共形不变性的判定方程(15)和(16)式，有

证毕.

4 应用例子

设非Chetaev型非完整约束系统的Tzénoff函数、约束方程和约束加在虚位移上的限制分别为

(22)

(23)

δq1-δq2=0

(24)

试研究该系统Mei对称性共形不变性和其能导出的守恒量.

解 由非Chetaev型非完整约束系统的Tzénoff方程(4)给出

(25)

利用(23)式求得

(26)

(25)式变为

(27)

有

(28)

和

(29)

由(27)式可得到

(30)

做计算

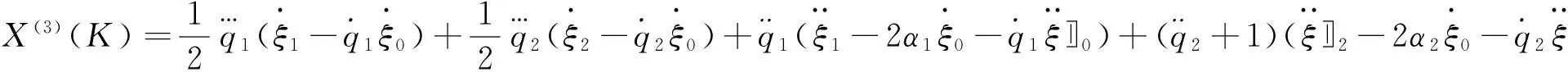
取生成元

(31)

有

(32)

(33)

故

(34)

由(33)和(34)式知，系统具有Mei对称性且同时具有Mei对称性共形不变性，其共形因子

(35)

结构方程(20)给出.

(36)

(21)式给出守恒量

5 结 语

本文研究了非Chetaev型非完整约束系统Tzénoff方程的Mei对称性共形不变性及其守恒量，在给出该系统Mei对称性定义和判据方程的基础上，进一步给出了系统Mei对称性共形不变性的定义和判据方程，并分析了二者之间的关系，发现只要恰当地选择无限小变换的生成元，可使系统既具有Mei对称性也同时具有Mei对称性的共形不变性.最后，导出了非Chetaev型非完整约束系统Tzénoff方程Mei对称性共形不变性存在守恒量的结构方程及其守恒量的具体形式.

参考文献：

[1]Mei Fengxiang.Form invariance of Lagrange system[J].Journal of Beijing Institute of Technology，2000，9(2)：120-124.

[2]梅凤翔.约束力学系统的对称性与守恒量[M].北京：北京理工大学出版社，2004.

[3]Fu Jingli，Wang Xianjun，Xie Fengping.Conserved Quantities and Conformal Mechanico-Electrical Systems[J].Chinese Physics Letters，2008，25(7)：2413-2416.

[4]Zhao Li，Fu Jingli.A new type of conserved quantity of Mei symmetry for the motion of mechanico electrical coupling dynamical systems[J].Chinese Physics B，2011，20(4)：040201(1-4).

[5]刘畅，赵永红，陈向炜.动力学系统Noether对称性的几何表示[J].物理学报，2010，59(1)：11-14.

[6]方建会.Lagrange系统Mei对称性直接导致的一种守恒量[J].物理学报，2009，58(6)：3617-3619.

[7]Li Yanmin.Lie Symmetries，Perturbation to Symmetries and Adiabatic Invariants of a Generalized Birkhoff System[J].Chinese Physics Letters，2010，27(1)：010202(1-4).

[8]Shao Kai Luo，Zhuang Jun Li，Wang Peng，Lin Li.A Lie symmetrical basic integral variable relation and a new conservation law for generalized Hamiltonian systems[J].Acta Mechanica，2013，224(1)：71-84.

[9]李凯辉，刘汉泽，辛祥鹏.一类高阶非线性波方程的李群分析、最优系统、精确解和守恒律[J].物理学报，2016，65(14)：140201(1-7).

[10]张丽香，刘汉泽，辛祥鹏.广义(3+1)维Zakharov-Kuznetsov方程的对称约化、精确解和守恒律[J].物理学报，2017，66(8)：080201(1-7).

[11]张晔，张毅，陈向炜.事件空间中Birkhoff系统的Mei对称性与守恒量[J].云南大学学报(自然科学版)，2017，39(2)：219-224.

[12]Галиуллин А С，Гафаров Г Г，Малайшка Р П，et al.Аналитическая Динамика Систем Гельмгольца，Виркгофа，Намбу：Монография[M].Москва：Редакция Журнала“Успехи Физических Наук”，1997.

[13]蔡建乐，梅凤翔.Lagrange系统Lie点变换下的共形不变性与守恒量[J].物理学报，2008，57(9)：5369-5373.

[14]刘畅，刘世兴，梅凤翔，郭永新.广义Hamilton系统的共形不变性与Hojman守恒量[J].物理学报，2008，57(11)：6709-6713.

[15]王廷志，韩月林.相对运动非完整动力学系统的共形不变性与守恒量[J].江南大学学报(自然科学版)，2013，12(2)：234-238.

[16]王小明，李元成，夏丽莉.机电系统Mei对称性的共形不变性与守恒量[J].贵州大学学报(自然科学版)，2009，26(6)：32-38.

[17]陈向炜，赵永红，刘畅.变质量完整动力学系统的共形不变性与守恒量[J].物理学报，2009，58(8)：5150-5154.

[18]李彦敏.变质量非完整力学系统的共形不变性[J].云南大学学报(自然科学版)，2010，32(1)：52-57.

[19]Zheng Shiwang，Jia Liqun，Yu Hongsheng.Mei Symmetry of Tzénoff Equations of Holonomic System[J].Chinese Physics，2006，15(7)：1399-1402.

[20]Zheng Shiwang，Xie Jiafang，Li Yanmin.Mei symmetry and conserved quantity of Tzénoff equations for nonholonomic systems of non-Chetaev，s type[J].Communications in Theoretical Physics，2008，49(4)：851-854.

[21]郑世旺，解加芳，陈向炜，等.完整系统Tzénoff方程的Mei对称性直接导致的另一种守恒量[J].物理学报，2010，59(8)：5209-5212.

[22]Zheng Shiwang，Wang Jianbo，Chen Xiangwei，Xie Jiafang.Mei symmetry and new conserved quantities of Tzénoff equations for the variable mass higher-order nonholonomic system[J].Chinese Physics Letters，2012，29(2)：020201(1-4).

[23]郑世旺，陈梅.非完整系统Tzénoff方程的Mei对称性所对应的一种新守恒量[J].云南大学学报，2011，33(4)：412-416.

[24]郑世旺，王建波，陈向炜，李彦敏等.变质量非完整系统Tzénoff方程的Lie对称性与其导出的守恒量[J].物理学报，2012，61(11)：111101(1-5).

[25]郑世旺，赵永红.完整系统Tzénoff方程Lie对称性的共形不变性与守恒量[J].商丘师范学院学报，2015，31(6)：39-43.

[26]郑世旺.变质量完整系统Tzénoff方程Mei对称性的共形不变性与守恒量[J].商丘师范学院学报，2016，32(12)：32-36.

[27]梅凤翔，刘端，罗勇.高等分析力学[M].北京：北京理工大学出版社，1991.