基于广义集值混合变分不等式的算法研究

肖成英，安士勇，李庆

(1.四川工商学院 云计算与智能信息处理重点实验室，四川 成都 611745;2.西南民族大学 计算机科学与技术学院，四川 成都 610041)

变分不等式自1966年被Hartman和Stampacchia首次提出并研究以来，已经得到国内外广大数学研究者的重视.从最初的古典变分不等式发展到现在的一般变分不等式、混合变分不等式、似变分不等式、变分包含等一系列相关问题.研究方法也在不断完善和提高，对每类变分不等式都建立了具体求解方法，主要包括投影法、超梯度法、辅助原理、预解方程.在Noor[1-3]中引入了解决混合变分不等式的预解方程技术.在[3]中证明了变分不等式和预解方程的等价性，利用等价性构造出混合变分不等式的迭代算法.文章利用预解方程技术证明广义集值混合变分不等式与不动点理论的等价性，以此构造出迭代序列，通过证明迭代序列的收敛性，从而证明广义集值混合变分不等式解的存在性问题.

随着变分不等式理论的成熟和发展，已经作为一个有效的工具，以统一的模式被大量地应用于力学、微分方程、现代化控制、经济管理科学、交通问题、对策理论等各个区域.变分不等式理论已成研究现代科学的重要工具.

1 提出问题

设H是实Hilbert空间，范数和内积分别为‖·‖，〈·，·〉，设g：H→H是单值映射，T：H→C(H)设集值映射，其中C(H)表示H的所有非空有界闭子集族，设泛函φ：H→R∪{+∞}是真凸下半连续，次可微的，其中∂φ表示φ的次微分.

本文要讨论的广义集值混合变分不等式：求u∈H，w∈T(u)，对∀v∈H，使得：

〈w，g(v)-g(u)〉+φ(g(v))-φ(g(u))≥0， ∀v∈H

(1)

特例：

(1)当g=I时，问题(1)变成下面的问题：找u∈H，T：H→C(H)，w∈T(u)，使得：

〈w，v-u〉+φ(v)-φ(u)≥0， ∀v∈H

(2)

问题(2)称为广义混合变分不等式，文献[4]中Noor证明了问题(2)等价于不动点问题，根据不动点理论构造出迭代序列，并证明序列的收敛性，从而得到(2)解的存在性.

(2)当g，T：H→H时，问题(1)变成下面的问题：找u∈H，使得：

〈Tu，g(v)-g(u)〉+φ(g(v))-φ(g(u))≥0， ∀v∈H

(3)

问题(3)称为第二类广义变分不等式，该变分不等式在纯理论和应用科学中许多线性和非线性问题中都得到了广泛的研究和应用.在文献[5]中Noor用校正法证明了迭代序列的收敛性和解的存在性.

(3)当T：H→H，g≡I时，问题(1)变成下面的问题：找u∈H，使得：

〈Tu，v-u〉+φ(v)-φ(u)≥0， ∀v∈H

(4)

问题(4)称为混合变分不等式，在文献[6]中，Noor用迭代法证明和分析了单调混合变分不等式解的存在性问题.对于问题的推广应用和方法可参见文献[7，8].

引理1[10]对z，u∈H，满足不等式

〈u-z，v-u〉+ρφ(v)-ρφ(u)≥0，∀v∈H

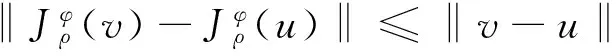
定义2[11]集值映射T：H→C(H)是Lipschitz连续，若存在常数ξ>0，使得：

‖w1-w2‖≤ξ‖u1-u2‖， 其中w1∈T(u1)，w2∈T(u2)

定义3[12]对u1，u2∈H，集值映射T：H→C(H)称为强单调，若存在常数α>0，使得

〈w1-w2，u1-u2〉≥α‖u1-u2‖2， 其中w1∈T(u1)，w2∈T(u2)

2 算 法

本节采用预解算子技术，将问题(1)转化为不动点问题，构造出迭代序列.在[13-16]中通过预解方程和不动点研究了关于混合变分不等式解的问题.

问题(1)等价于下面的不动点问题：

定理1若u是问题(1)的解当且仅当u满足下面的等式：

(5)

证明：设u是问题(1)的解，则有：

〈w，g(v)-g(u)〉+φ(g(v))-φ(g(u))≥0，

即φ(g(v))-φ(g(u))≥〈-w，g(v)-g(u)〉

由∂φ(u)的定义，上式成立当且仅当：-w∈∂φ(g(u))

注：定理1还可表示为：

通过此不动点方程构造出下面的迭代算法：

算法1设T：H→C(H)是集值映射，g：H→H是单值映射，设泛函φ：H→R∪{+∞}是真凸下半连续，次可微的，其中∂φ表示φ的次微分，u0∈H，w0∈T(u0)，对∀v∈H，设

由Nadler[17]，存在w1∈T(u1)，满足：

由此得到序列{un}，{wn}

其中

(6)

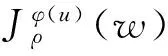
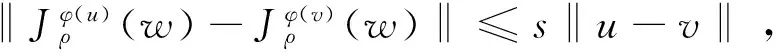
3 解的存在性及迭代序列的收敛性

本节根据算法1构造的迭代序列，通过证明序列的收敛性，从而证明问题(1)解的存在性.

定理2设T：H→C(H)是集值映射，且T是α-强单调和ξ-Lipschitz连续的；g：H→H是单值映射，且g是δ-强单调和σ-Lipschitz连续的；泛函φ：H→R∪{+∞}是真凸下半连续，次可微的，其中∂φ表示φ的次微分，若假设1成立且满足：

(7)

则由算法1产生的迭代序列：{un}，{wn}分别收敛于u，w，且u，w就是变分不等式(1)的解.

证明：

(8)

由于g是δ-强单调和σ-Lipschitz连续的，所以有：

‖g(un)-g(un-1)‖≤σ‖un-un-1‖； 〈g(un)-g(un-1)，un-un-1〉≥δ‖un-un-1‖2

则

‖un-un-1-(g(un)-g(un-1))‖2=‖un-un-1‖2-2〈g(un)-g(un-1)，un-un-1〉+‖g(un)-g(un-1)‖2≤

‖un-un-1‖2-2δ‖un-un-1‖2+σ2‖un-un-1‖2=(1-2δ+σ2)‖un-un-1‖2

(9)

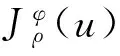
s‖un-un-1‖+‖g(un)-g(un-1)-ρ(wn-wn-1)‖≤

s‖un-un-1‖+‖un-un-1-(g(un)-g(un-1))‖+‖un-un-1-ρ(wn-wn-1)‖≤

(10)

由定义2和定义3，T是α-强单调和ξ-Lipschitz连续的，则

‖un-un-1-ρ(wn-wn-1)‖2=‖un-un-1‖2-2ρ〈wn-wn-1，un-un-1〉+ρ2‖wn-wn-1‖2≤

‖un-un-1‖2-2ρα‖un-un-1‖2+ρ2ξ2‖un-un-1‖2=(1-2ρα+ρ2ξ2)‖un-un-1‖2

所以

(11)

将(11)带入(10)，得

(12)

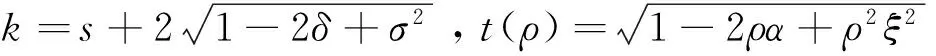
将(9)和(12)带入到(8)，得

(13)

令γ=(k+t(ρ))，由(7)知0<γ<1

因此，由(13)知{un}是柯西收敛序列，∃u∈H，使得un→u

由(6)及T的Lipschitz连续性，有

wn∈T(un)，，‖wn+1-wn‖≤ξ(1+(n+1)-1)‖un+1-un‖

所以{wn}也是柯西收敛序列，∃w∈T(u)，使得wn→w

由(5)知(u.w)是问题(1)的解.

参考文献：

[1]Noor M A.Theory of Variational inequalities[M].Lecture Notes，Mathematics Department，King Saud University，Riyadh，Saudi Arabia，1997.

[2]Noor M A.Some recent advances in Variational inequalities[J].Part I，Basic concepts，New Zealand J.Math,1997,26(1)：53-80.

[3]Noor M A.Some recent advances in Variational inequalities[J].Part ∏，Other concepts，New Zealand J.Math,1997,26(4):25-56.

[4]Noor M A.Generalized monotone mixed variational inequalities[J].Mathematical and Computer Modelling,1999,29:87-93.

[5]Noor M A.Some algorithms for general monotone mixed variational inequalities[J].Mathematical and Computer Modelling,1999,29:1-9.

[6]Noor M A.A new iterative method for monotone mixed variational inequalities[J].Mathematical and Computer Modelling,1997,26:29-34.

[7]Noor M A.Algorithms for general monotone mixed variational inequalities[J].J.Math.Anal.Appl,1999,229:330-343.

[8]Giannessi F.and Maugeri A.Variational inequalities and Network Equilibrium Problems[M].Plenum Press，New York，1995.

[9]Brezis H.Operateurs maximaux monotones et semigroups de contractions dans les Espaces de Hilbert[M].North-Holland，Amsterdam，1973.

[10]张石生.变分不等式及其相关问题[M].重庆：重庆出版社，2008：20-48.

[11]Fang Y P，Huang N J，and Thompson H B.A new system of variational inclusions with(H，η)-monotone operators in Hilbert spaces[J].Comput.Math.Appl,2005,49(2-3):365-374.

[12]Xiao Cheng-ying，Min Lan and Deng Lei.Self adaptive methods for set-valued Mixed variational inequalities[J].Journal of Southwest University，2007,29(8):18-21.

[13]Ding X P.Generalized implicit quasivariational inclusions with fuzzy set-valued mappings[J].Comput.Math.Appl,1999,38(1):71-79.

[14]Huang N J,Deng C X.Auxiliary principle and iterative algorithms for generalized set-valued strongly nonlinear mixed variational-like inequalities[J].J.Math.Anal.Appl,2001,256:345-359.

[15]Kazmi K R.Mann and Ishikawa.perturbed iterative algorithms for generalized quasivariational inclusions[J].J.Math.Anal.Appl,1999,209:572-587.

[16]Noor M A.Multivalued variational inequalities and resolvent equations[J].Math.Comput.Modelling,1997,26(7):109-121.

[17]Nadler S B.Multi-valued contraction mappings，Pacific J.Math,1969,30:475-488.

[18]Noor M A.Set-valued mixed Quasi-variational inequalities and implicit resolvent equations[J].Mathematical and Computer Modelling,1999,29:1-11.