基于函数P-集合的信息规律积分度量

郭志林，王宁

(商丘师范学院 数学与统计学院，河南 商丘 476000)

0 引 言

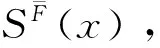
换句话说，若信息规律发生变化，利用函数P-集合能得到什么研究结果？如果给定区间[a，b]上的信息规律发生上下移动，函数P-集合如何度量？要求信息规律稳定，函数P-集合能给予什么样的帮助？凡是研究信息规律的人们，都想得到这些问题的答案.本文首次将积分[8，9]概念引入到具有动态特性和规律特征的函数P-集合中，给出信息规律曲线的积分度量，提出上、下漂移规律的概念和积分度量下规律偏离度，偏离率的概念，给出函数P-集合的规律生成定理，漂移规律关系定理和偏离规律恢复-还原定理，给出规律变化的量化表示.并利用这些结果，给出信息规律在风险投资中的应用.

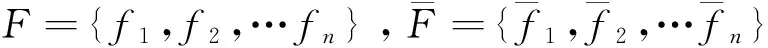
1 函数P-集合与信息规律生成

(1)

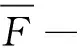
(2)

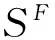
(3)

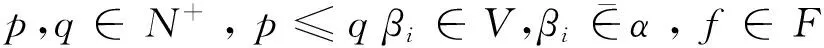
给定函数集S={s1，s2，…，sq}⊂U，α={α1，α2，…，αk}⊂V是S的属性集，称SF是S生成的函数外P-集合，而且

SF=S∪S+={s1，s2，…，sr}

(4)

S+称作S的F-函数补充集合，而且

(5)

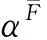
(6)

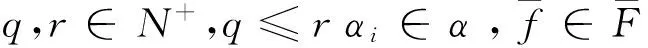
(7)

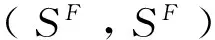
利用式(1)-式(6)，得到定理1和定理2.

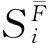
(8)

则

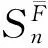
(9)

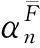
(10)

则

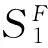
(11)

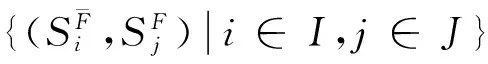
有关函数P-集合及P-集合的性质及应用，请参考文献1，6，7，10-15.

定义1给定函数集S={s1，s2，…，sq}⊂U，α={α1，α2，…，αk}⊂V是S的属性集，∀si∈S的离散形式

si(1)，si(2)，…，si(n)

(12)

得到S={s1，s2，…，sq}的离散形式

(13)

将上式记作y1，y2，…，yn，得到数据点

(x1，y1)，(x2，y2)，…，(xn，yn)

利用Lagrange插值函数

(14)

得到P(x)=an-1xn-1+an-2xn-2+…+a1x+a0，称P(x)是S生成区间[a，b]上的规律.

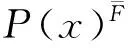
(15)

称P(x)F是P(x)的上漂移规律，如果P(x)F是函数外P-集合SF={s1，s2，…，sr}生成区间[a，b]上的规律，而且

P(x)F(x)=cn-1xn-1+cn-2xn-2+…+c1x+c0

(16)

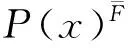
(17)

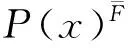
(18)

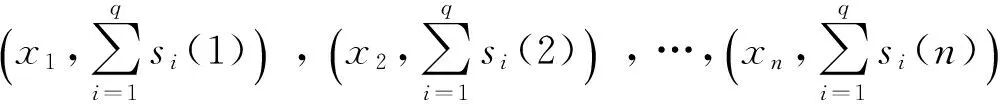
(19)

利用插值函数，得到

P(x)=an-1xn-1+an-2xn-2+…+a1x+a0，

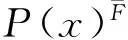
(20)

利用插值函数，得到

因为p≤q，由式(19)、式(20)得到

定理4(上漂移规律关系定理)若P(x)是S生成区间[a，b]的规律.P(x)F是P(x)的上漂移规律，则

P(x)≤P(x)F

(21)

证明 类似定理1，略.

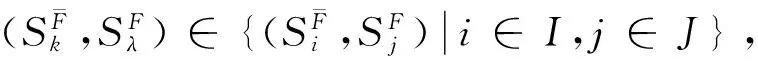
(22)

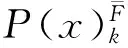
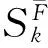
(23)

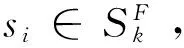
(24)

因为p≤r，由式(21)、式(22)得到

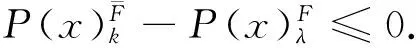
由定理1和定理2不难得到：

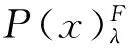
(25)

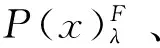
(26)

2 信息规律的积分度量

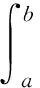
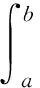
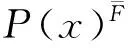
这时需要指出：如果P(x)是现实系统中的规律(如经济系统中的利润规律)，那么，规律P(x)的积分度量就是该规律的二维度量，利用它可以对规律的变化给出量化的表示.

(27)

定义6称r(x)F为上漂移规律P(x)F关于规律P(x)的偏离规律，简称上偏离规律，如果

r(x)F=P(x)F-P(x)

(28)

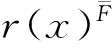
(29)

定义7称DF为上漂移规律P(x)F关于规律P(x)的偏离度，简称上偏离度，如果

(30)

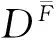
(31)

定义8称μF为上漂移规律P(x)F相对于规律P(x)的偏离率，简称上偏离率，如果

(32)

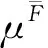
(33)

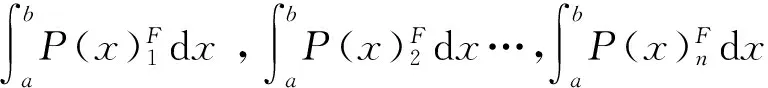
(34)

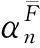
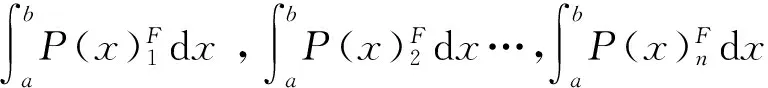
(35)

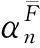
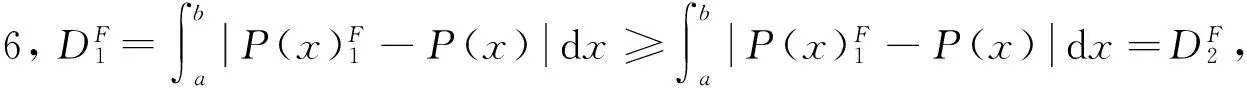
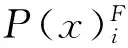
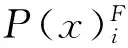
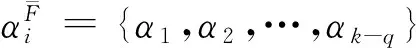
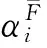
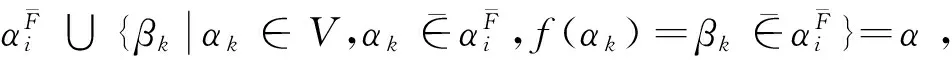
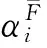
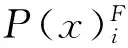
(36)

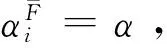
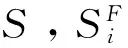
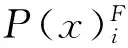
(37)

定理10，定理11由定理8，定理9容易得到，证明略.

对于下漂移规律，类比可得到类似结论.

3 信息规律积分度量在利润风险识别中的应用

在风险投资评估系统中，系统外一些人们意想不到的风险因素可能会突入其来地侵入到该系统中，这些意想不到的风险因素对风险投资具有极强的破坏性，使风险投资决策的成功率降低；与此同时，受某些方面的影响，系统中的有些风险因素可能会在风险评估系统中的影响力降低甚至消失，从而不再属于风险因素集的范畴，不考虑这样的情况，可能会使风险投资决策过于保守，甚至错失投资机会.随机P-集合就揭示了这样的事实.

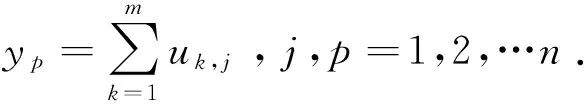
投资与利润值的获得是一个时滞过程，在这一过程中，投资环境的改善或恶化会使投资系统的输出规律(实际利润)会出现一定程度的偏离.投资系统S的属性值发生变化，相应的利润规律也会发生改变.它警告人们，风险因素的存在和入侵引起的利润规律的偏离成为风险投资系统控制的关键.

为了简单，又不失一般性，本节只给出下漂移规律在风险投资系统中的应用.本节的例子取自某投资公司2012年1—6月的利润.在风险投资系统，系统状态总是在不停的变化，正常情况下，会稳定在一定的范围内.设系统S={s1，s2，…，st}，S的属性集是α={α1，α2，α3，α4}.在时间段[1，6]等距的取其预设的利润净值点的数据(1，10.1175)，(2，12.8021)，(3，13.1075)，(4，14.9632)，(5，13.6224)，(6，17.1238).

其中利润净值点数据经过技术处理，这并不影响所要讨论的结果.

P(x)=0.1788x5-3.0442x4+19.4721x3-58.0129x2+80.5376x-29.0139.

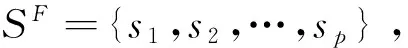
(1，8.9674)，(2，10.8835)，(3，10.8607)，(4，11.4945)，(5，10.6985)，(6，12.9096).

由于风险属性的入侵，使得实际利润规律与预设利润规律发生偏离，偏离规律为

在该时间段内，实际利润规律相对于设定利润规律P(x)的偏移度

实际利润规律相对于设定利润规律P(x)的偏移率

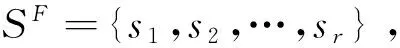
实际利润规律

风险属性α5的入侵，使得利润规律发生偏离，偏离规律为

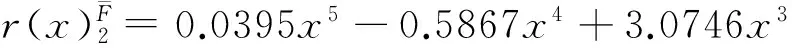
在该时间段内，实际利润规律相对于设定利润规律P(x)的偏移度

偏离率

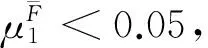
利润规律的偏离度量给出了风险投资系统受外部因素干扰的量化表示.投资公司可根据市场大环境通过设置利润系统偏离的阈值μ来限制风险投资系统利润规律出现的偏离.本例取自人们司空见惯的经济系统.本文的例子，稍加改进、扩展，便可应用到到信息系统其他研究领域.

4 结束语

在金融投资系统中，利润规律不是一成不变的，它总是不断地上下震荡，利润规律的震荡来自投资环境的变化，这是人们都知道的事实.如果把函数P-集合引入到利润规律之中，能够得到一些符合实际的结果.利用函数P-集合所具有的动态特性和规律特性去研究金融投资系统利润规律的变化，可使人们看到金融投资系统的风险性.本文把基于函数P-集合的规律积分特性引入到金融投资系统，提出基于函数P-集合的漂移规律生成的概念和漂移规律积分度量的概念，讨论了规律上、下漂移引起的系统偏离度和偏离率的变化情况，为利润规律的随机变化给出了量化表示，为下一步的投资决策奠定了基础，为函数P-集合的应用提供了一个新的研究方向.

参考文献：

[1]史开泉.函数P-集合[J].山东大学学报(理学版)，2011，46(2)：62-69.

[2]史开泉.P-集合[J].山东大学学报(理学版)，2008，43(11)：77-84.

[3]SHI Kaiquan.P-sets and its applications[J].An International Journal Advances in Systems Science and Applications，2009，9(2)：168-178.

[4]史开泉，姚炳学.函数S—粗集与规律辩识[J].中国科学E：信息科学，2008，38(4)：553-564.

[5]史开泉，赵建立.函数S—粗集与规律安全-认证[J].中国科学E：信息科学，2008，38(8)：1234-1243.

[6]林蓉，史开泉.函数P-集合及及信息规律的属性控制[J].计算机科学，2012，39(7)：225-228.

[7]林蓉，范成贤.函数P-集合与信息规律动态特征[J].山东大学学报(理学版)，2012，47(1)：121-126.

[8]郭志林.Fp-规律与Fp-规律积分度量[J].烟台大学学报(自然科学与工程版)，2010，23(4)：260-264.

[9]郭志林.一元F-粗积分的概率估计[J].模糊系统与数,2010，24(5)：111-116.

[10]史开泉.内P-集合和它的应用特征[J].计算机科学，2010，37(8)：1-8.

[11]张丽，崔玉泉，史开泉.外P-集合和数据内恢复[J].系统工程与电子技术，2010，32(6)：1233-1238.

[12]张飞，陈萍，张丽.P-集合的P-分离与应用[J].山东大学学报(理学版)，2010，45(3)：83-92.

[13]于秀清.内P-集合与安全的信息传递[J].计算机应用与软件，2012，29(8)：122-125.

[14]刘若慧，刘保仓，史开泉.外P集合与F_信息伪装[J].系统工程与电子技术，2011，33(1)：116-119.

[15]于秀清.内P-集合与F-内嵌入信息发现-辨识[J].系统工程与电子技术，2012，34(6)：1200-1204.